边缘检测在多聚焦图像融合中的应用
王晨昊, 沙 欣, 陈 丹
(1.陕西省交通规划设计研究院 智能交通工程设计研究所, 陕西 西安 710065;2.西安理工大学 自动化与信息工程学院, 陕西 西安 710065)
在同一场景中,对不同对象进行单独聚焦拍摄,再将得到的不同聚焦对象融合在一起的技术就是多聚焦图像融合技术。小波变换作为多聚焦图像融合中的一种常用技术,近年来取得了诸多进展。文献[1]利用多尺度小波变换和稀疏表示相结合的方式,分别研究了多聚焦图像、医疗图像、红外图像的融合性能;文献[2]将小波变换和彩色空间变换结合在一起,实现彩色多聚焦图像融合质量的提升,原图像经小波变换后得到低、高频系数;文献[3]改进了高频融合规则,以基于区域特征的融合算法对高频系数进行处理;文献[4]利用分步稀疏表示和小波变换相结合的方法研究了全色多尺度光谱图像的融合。但是小波变换分解原图像的过程,实际上是对原图像中蕴含信息的一系列滤波[5]。在这一过程中,蕴含图像大部分边缘信息的低频系数,往往没有得到足够的细化,导致融合图像的边缘细节不够突出[6]。针对这一问题,本文将Canny边缘检测算法与小波变换相结合,利用Canny边缘检测算法提取经小波分解后低频系数中的边缘信息,将这部分信息与代表图像细节的高频部分以绝大值法处理,低频部分以平均数法处理,最后经过仿真实验,从信息熵、平均梯度、标准差、空间频率等方面对其融合效果性能做出评价。
1 小波变换图像融合的影响因素
基于小波变换图像融合的步骤如下:
(1)选择小波基对原图像进行小波变换,得到代表原图像轮廓信息的低频系数和代表原图像细节信息的高频系数;
(2)选取融合规则对低、高频系数进行处理,获得不同成分的子系数;
(3)对子系数以小波逆变换处理,得到融合图像。
在上述过程中,小波基的选择是决定图像融合效果的重要因素之一。针对这一因素,本文设计了如下仿真实验。仿真中小波分解层数统一为3层,使用平均数法作为低频融合算法,绝对值后取最大值作为高频融合算法。选取信息熵、平均梯度、标准差和空间频率作为评价标准[7],融合结果如图1所示。

图1 采用不同小波基的融合结果图像
不同小波基的融合图像结果评价见表1,其中信息熵表示图像蕴含信息的多少,信息熵越高,图像蕴含的信息越多[8]。平均梯度通过衡量融合图像的细节变化评价融合图像的清晰度[9],平均梯度越高,图像对细节对比的表达能力越强,图像也就越清晰。标准差的大小与图像质量相关,相当于图像分辨率,标准差越大,表示图像灰度级分布越分散,图像的有用信息就越多。而空间频率则反映了一幅图像在空间域的活跃程度[10],一幅图像的空间频率越高,则其融合效果越好。从表1中的数据可以看出,Db4小波与Haar小波相比,仅在空间频率上略低,其余各项均优于Haar小波。而相比于Bior2.4、Bior4.4两种小波,Db4小波各项数据均占优势。故本文使用Db4小波作为小波基。
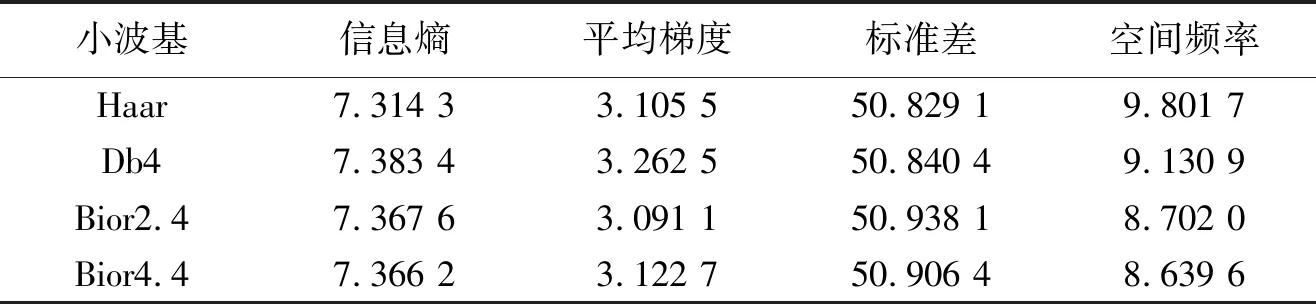
表1 不同小波基的融合图像结果评价
2 基于边缘检测的小波变换图像融合
基于小波变换的多聚焦图像融合是通过小波变换将原图像分解为一个低频系数和多个高频系数,对不同频段系数使用不同的融合规则进行处理后,再通过小波逆变换得到融合图像。在这一过程中,小波变换分解原图像得到的高频系数没有进一步的细分和量化,丢失了原图像中的一部分细节信息[5]。而低频系数包含原图像大部分信息,可以表征原图像的边缘轮廓。因此,本文通过Canny边缘检测算法提取低频系数中的边缘图像,再通过绝大值系数法与高频系数内相应分辨率的图像融合,达到提升融合图像质量的目的。
2.1 Canny边缘检测算法
常用的一阶梯度算子有Roberts、Prewitt、Sobel,这些算子虽然容易实现,但去噪能力较差,容易出现伪边缘且检测精度不高[5]。John Canny提出的Canny算子是一种含有很强的去噪能力和较高的检测精度的算子,并且成为了评价其他边缘检测方法的标准。Canny边缘检测算法主要包括以下4个步骤:
(1)设原始图像为f(x,y),原图像经高斯滤波器平滑处理后的图像G(x,y)表示为
G(x,y)=f(x,y)*H(x,y),
(1)
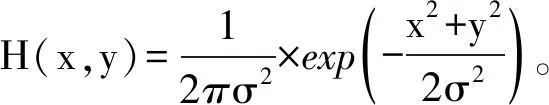
(2)利用Sobel算子模板:
计算得到G(x,y)梯度的幅值φ(x,y)和θφ方向:
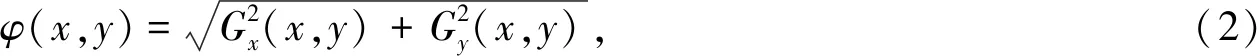

(3)对计算得到的梯度幅值φ(x,y)进行非极大值抑制,保留φ(x,y)内不同范围梯度幅值最大的点φm(x,y),细化边界信息。
(4)对φm(x,y)选取两个阈值TH和TL,TL/TH=1/2。将φm(x,y)中梯度幅值小于TL的点置0,梯度幅值大于TH的点置1,即可提取出完整边缘。
2.2 基于边缘检测的小波变换图像融合
通过小波变换将多聚焦原图像分解为低频系数和高频系数,使用Canny边缘检测算法提取低频系数中包含的边缘轮廓细节后,对低频系数以平均数法进行处理,再将提取出的边缘轮廓细节与高频系数内相应分辨率的点通过绝大值系数法进行处理,最后通过小波逆变换得到融合图像。
低频系数平均数法表示为

其中f1(m,n)、f2(m,n)表示原图像分解后在对应的(m,n)上的小波系数,f3(m,n)表示结果图像在(m,n)上的小波系数。
高频系数绝大值法表示为
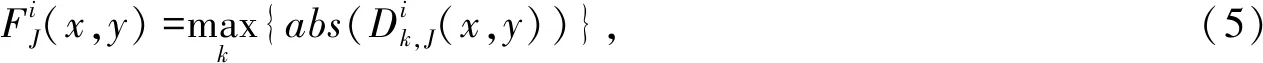
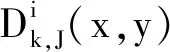
图2是基于边缘检测的小波变换图像融合方法流程图。
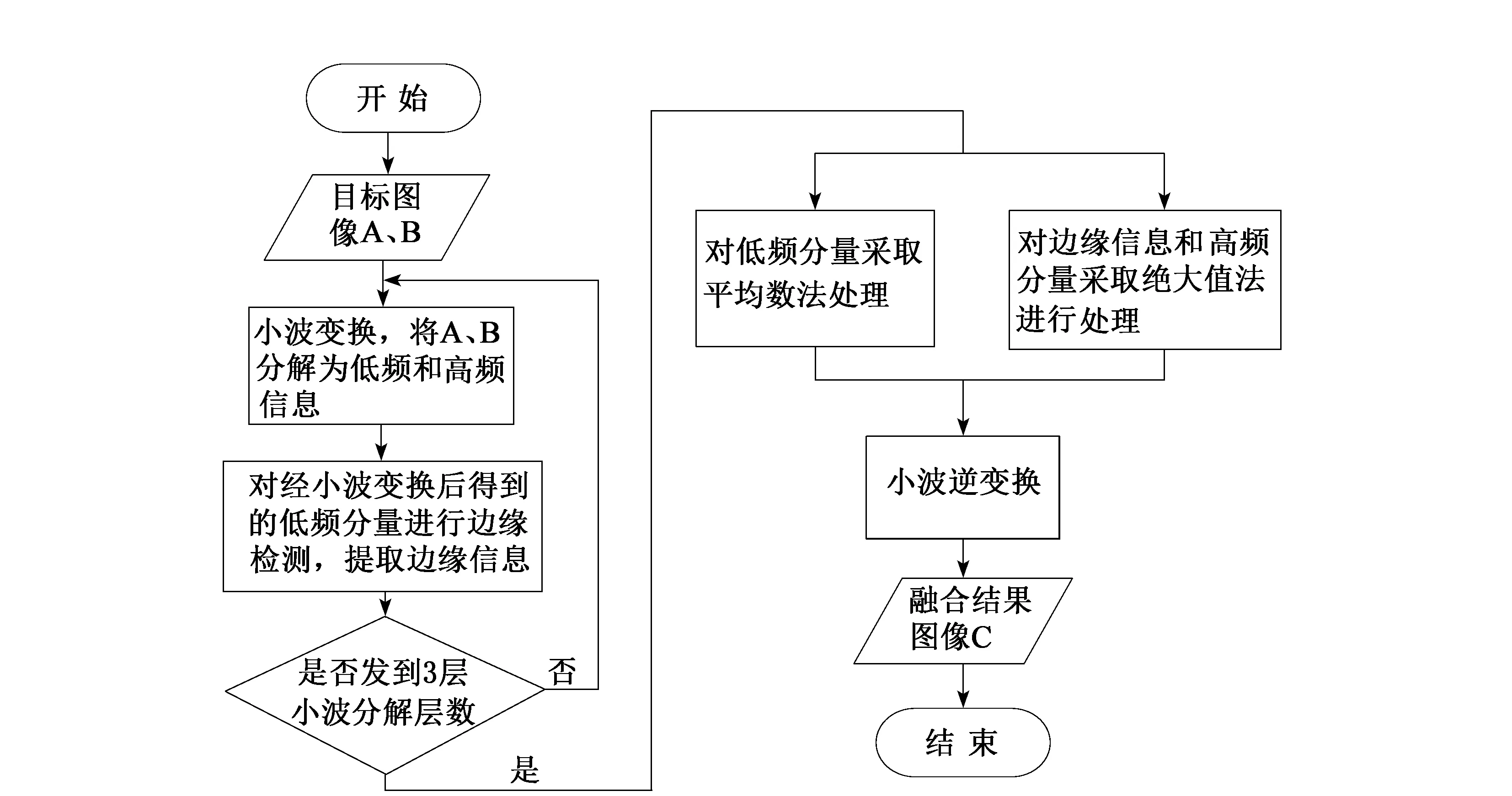
图2 图像融合方法流程图
3 仿真结果与分析
仿真中使用两种算法对多聚焦图像进行融合,小波基统一选择Db4,分解层数为3层。算法1使用小波变换分解原图像,对分解后得到的低频系数以平均数法进行处理,对高频系数以绝大值法进行处理。算法2为本文所述算法。仿真结果如图3所示。
表2是对图3中(c)、(d)两幅融合结果的评价,从数据可知图3(d)的评价结果均优于图3(c)。同时,通过人眼的主观评价可以观察到图3(d)中图像的边缘和轮廓比图3(c)中更为清晰。

图3 部分模糊的实际拍摄景物图像及融合结果

融合结果信息熵平均梯度标准差空间频率算法17.352 86.542 144.715 620.122 5算法27.391 47.744 247.740 925.080 0
由于人脸包含着非常丰富的轮廓信息和细节,如人的脸型、眼睛的形状、眉毛和胡茬的清晰度等,在图像融合的过程中更能体现所使用方法的优越性,因此选用如图4中(a)、(b)所示的不同位置模糊的彩色人脸图像,通过仿真实验体现本文使用的算法在融合结果中对原图像细节信息的提升。

图4 部分模糊的人脸图像及融合结果
如表3所示,在上述算例中,使用本方法得到的融合结果图像,从信息熵、平均梯度、标准差、空间频率等4个方面均优于使用传统小波变换图像融合方法后得到的结果图像。同时,在主观评价(即人眼)中,本方法的结果图像,尤其是在圈出内的人眼及眉毛部分,如图4(d)的圈内部分,相比于使用算法1的结果图像(图4(c)的圈内部分),图4(d)有着更加清晰的边缘和轮廓。此外,通过观察给出的两种图像中两种方法的结果图像图4(e)、(f),可以发现在使用传统方法的结果图像中,出现了噪声点,而在本方法的结果图像中,没有噪声点,造成这一结果的原因为经边缘检测提取到的边缘信息在与高频分量以绝大值法处理的过程中,噪声点得以过滤。同时,在边缘检测提取边缘信息的过程中,Canny边缘检测算子可以被看作一个基于梯度的滤波器,在滤出边缘点的过程中,噪声点也会被过滤。

表3 评价参数的对比
4 总 结
本文所使用的融合方法对原图像经过小波分解后,得到的低频分量进行了边缘检测,将提取的边缘信息与高频分类以绝大值法进行处理,低频分量以平均数法进行处理,因此本方法在处理包含较多细节信息的彩色图像上,相比于同类算法,可以有效提高融合后图像细节的清晰度,具有算法结构简单、易于实现的特点。同时,由于边缘检测这一处理过程,可以在一定程度上减少融合结果图像的噪声点,具有独特的优越性。

