A New Design Approach for Nearly Linear Phase Stable IIR Filter using Fractional Derivative

Nikhil Agrawal,, Anil Kumar,, and Varun Bajaj,

Abstract—In this paper, a new design method for digital infinite impulse response (IIR) filters with nearly linear-phase response is presented using fractional derivative constraints (FDCs). In the proposed method, design problem of an IIR filter is constructed as the minimization of phase error between the desired and designed phase response of an allpass filter (APF) such that the designed lowpass filter (LPF) or highpass filter (HPF) yields less passband (ep), and stopband errors (es) with optimal stopband attenuation (As). In order to have accurate passband (pb) response,FDCs are imposed on appropriate reference frequency, where the optimality of these FDCs are ensured by using a new greedy based sorting mechanism. The simulated results reflect the efficiency of the proposed method in term of improved passband response along with better transition width. However, small reduction in As is observed within the allowable limit, when compared to non-fractional design approach, but the designed filter remains immune to wordlength (WL) effect.

I. Introduction

Asubstantial progress has been made towards digital signal processing like blind source separation of audio signals [1], automatic fault detection [2] and numerous other applications. Marked progress has been made in the design of digital filters for numerous applications such as system identification, denoising, adaptive filtering and efficient design of multirate systems [3], [4]. In general, there are two types of digital filters: infinite impulse response (IIR) and finite impulse response (FIR) filters. In some applications such as channel equalization, low-delay filtering, and seismic migration, IIR filters are extensively used due to much sharper transition region roll-off, and low memory requirement as compared to FIR filters. Therefore, several attempts were made to improve the performance of IIR filters [5]–[7]. These techniques have been broadly classified into two types: conventional approach and computer aided design (CAD) technique. In conventional techniques, a prototype lowpass analog filter is designed, and transformed into digital domain using suitable approximation. These techniques are quite fast,however they suffer from finite word length (WL) effect, nonlinear phase, and wrapping effect [8]. Therefore, to address these issue, several computer aided design techniques were proposed for IIR filters, which can be further sub-categorized into gradient based [9]–[11] and evolutionary based techniques [7], [12], [13].

The first gradient based technique using linear programming(LP) was presented for designing a digital IIR filter in [14].This technique was further improved to include the stability constraint, and linear phase response. Another technique using the weighted least square (WLS) technique was proposed to design IIR filters with Equiripple response [9], while in [10],authors have devised a new design procedure, based on peakconstrained least square (PCLS) criterion using recursive quadratic programing (RQP) with generalized multiple exchange (GME) to optimize frequency response and group delaysimultaneously. This design procedure was further improved to achieve equiripple response in passband by employing three constraint factors [15]. In this technique, a quadratic error function using these three constraint factors:stability, maximum ripple in stopband, and equiripple in passband, was minimized. This error function was further utilized by several researchers for designing an IIR filters with improved performance [11]. Minimax criteria was used with gradient based techniques as second order con-programing(SCOP) for efficient filter response [16]–[19]. Thus, it is evident from literature review on gradient based techniques that several methods have been developed for an IIR filters. In all these methods, a non-linear error surface function has been formulated either in frequency domain or time domain, and translated into a convex surface, which can be solved by gradient based techniques. Therefore, the solutions resulted from these techniques were sub-optimal due to trapping in local minima. Hence, gradient based methods are not suitable choice for an IIR filter design, in which the error function is a multi-modal and non-differentiable error function. The modern heuristic search methods, known as evolutionary techniques (ETs) such as genetic algorithm (GA), particle swarm optimization (PSO), artificial bee colony (ABC)algorithm, and cuckoo search (CS) algorithm are found to be an efficient methods for finding solution of non-differentiable optimization problems, and therefore, they have been extensively used for filter design during the past few decades[20], [21].

In this context, the first systematic ET, named as GA was used for minimization of absolute error, computed in frequency domain for designing digital IIR filters, however this technique was suitable for designing digital filters with lower order [7]. Since then, several modifications were made in GA, and tested with various objective or error function to obtain good designs of IIR filters [8], [13], [22], [23].However, GA was more prone to premature convergence,involves too many functions evaluation, and has high dependence on initially formed search space, which yields in sub-optimal solution with more computational complexity.Then, several other optimization techniques such as PSO,ABC algorithm, differential evaluation (DE) and CS algorithms were exploited to achieve desired frequency response of an IIR filter [12], [21], [24]. These, ETs were suitable for lower order system, and also suffer from suboptimal fixing for large-scale optimization with high variations in design results. However, in [25] authors have studied the effect of control parameters and shown that by adjusting these parameters, CS algorithm is able to design higher order filters. Subsequently, several researchers have proposed improved hybrid techniques based on hybridization of two optimization techniques such as PSO with DE, and PSO with GA [26], [27]. A new hybrid technique was also presented based on PSO and DE with binary search algorithm for designing an optimal IIR filter [28]. Recently another hybrid method using PSO and ABC algorithm has been developed for designing an IIR filter with low quantization error [29]. Thus, it is evident from evolutionary techniques reported so far in literature that designing an IIR filter using ETs was effective for a digital filter having lower order, nonlinear phase response, and requires too many evaluations to achieve desired solution. In the hybrid techniques, complexity was too high as both local and global searches were conducted using two different optimization techniques.

Based on the reviewed literature, it has observed that an IIR filter has a much sharper transition region, and low memory requirement than a FIR filter, even though FIR filters are more preferred due to linear phase characteristic. Therefore, to achieve linear-phase response with more accurate performance of an IIR filter, a new design approach using an all-pass filter (APF) was developed in [30], [31]. Similarly,another technique using an APF, based on minor component analysis (MCA) was proposed for the design of IIR filters and quadrature mirror filterbanks [32]. These techniques are efficient for designing linear-phase response filters, however attenuation at passband edge frequencyis quite high,causing high error in passbandTherefore, there is strong motivation to develop a new design technique for an IIR filter,which can improve performance in passband region.

During past few decades, fractional derivatives (FDs) have emerged as an application orientated branch of calculus,which gives more flexibility to derivative operation by replacing integer order of conventional derivative with real order. Therefore, fractional order based system were proposed, which met the required performance with reduced order and more stability than conventional integer order system. In this context, authors designed stable fractional order based digital IIR differentiator, whereas in [33]–[35]authors proposed methods for fractional order integrator with improved stability [36]. Several researchers have used fractional derivatives for various applications of signal and image processing for solving linear and non-linear problems[37], [38]. Authors in [39] have proposed a new method for designing FIR filters to obtain more accurate response at the desired frequency using the Lagrange multiplier method and fractional derivative constraints (FDCs). This technique has been extended for the design of 2-dimensional (2-D) linear phase FIR filters in [40]. Authors in another research [41]have presented a new technique for designing of FIR filters for given magnitude and phase responses using FDCs. These methods yield the improved filter performance as compared to an eigen filter design approach, however they were not computationally efficient as fractional orders of derivatives have been selected based on trial and error method. Therefore,a new technique has been presented for designing FIR filters,based on FDC and nature-inspired optimizations [42]. This technique was further extended for designing two-channel filterbanks [43] and cosine modulated filterbanks [44].Recently, a new technique has been devised for designing linear phase quadrature mirror filterbanks using polyphase components and fractional derivatives [45]. In these techniques [42]–[45], Lagrange multiplier method and fractional derivatives were used, and optimal values of FDCs were computed using evolutionary algorithms.

Based on the literature review of IIR filters, it is evident that several efforts have been made on investigating, and developing new design method for improving the performance of IIR filters in numerous applications. Linear phase design of an IIR filter is still a challenging task due to denominator polynomial in its transfer function. Optimal response with a linear phase is principal requirement for filtering of various signals. As discussed above, authors in [31] have presented the first systematic approach for designing a nearly linear phase IIR filter using APF. Although, an IIR filter with nearly linear phase characteristic with high stability, has so far received limited attention. Several fractional order based design for IIR systems were proposed, however fractional derivative based design of an IIR filter with integer order is yet not considered. It has also evident from literature that an IIR filters designed using gradient optimization has nearly linear phase, however its response is highly sensitive towards quantization of filter coefficients. Whereas, the design based on evolutionary techniques result in improved passband and stopband region, but linear phase response is not guaranteed.

Therefore, in this paper, a new design technique for IIR filters with nearly linear phase characteristic is presented using FDCs. The exploitation of FD helps in obtaining high accuracy in the passband by controlling attenuation nearThe filter coefficients of a nearly linear phase IIR filter are computed using the Lagrange multiplier, which is computationally efficient as compared to eigen vector approach. Performance of designed filter is not degraded due to quantization and truncation of filter taps. A new greedy based search method is also explored with the proposed strategy for determining sustainable fraction value of FDCs.

II. Designing of IIR Filter using APF

Consider an IIR filter transfer function, denoted ascan be expressed as a parallel connection of an APF, defined as [31]

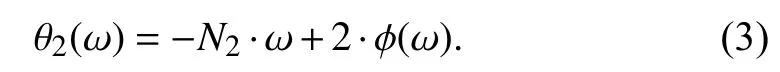
and similarly, for a HPF, it is computed by

To achieve more precise passband response, the phase error between a delay function and APF should be zero in passband regionand it should equal toin stopband region. An APF exhibits mirror image symmetry between numerator and denominator polynomials, therefore phase response of denominator polynomial is sufficient to design an appropriate filter response, and defined by (7) for LPF and (8) for HPF [31]

and

Generally, for designing a LPF or HPF IIR filter, the least square (LS) criterion ornorm is exploited. For this purpose, the phase response of denominator polynomial of an APF transfer function, defined in (3), is computed as [31]

and this can also be reframed as

After rearranging the above equation, the design problem may be considered as an inner product of vectors:

or

As designing of an IIR filter is executed by evaluation ofnorm:Therefore, the design problem of a LPF or HPF, is reduced to optimization of an error functiondefined as [31]

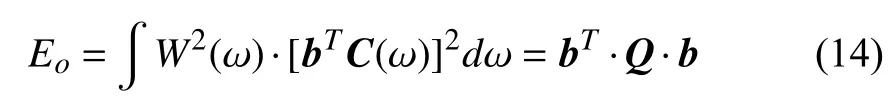
For solving (14), eigen vector may be computed formatrix, defined as

In above equation,Qis a positive, real, and definite matrix.An eigen vector corresponding to the least value of eigen value ofQ, contains the coefficients of an APF. In order to make more accurate response in passband, in this work, FDs are incorporated using Lagrange multiplier method.

III. Fractional Derivative (FD)

A marked progress has been made towards development and applications of fractional derivatives (FDs) in past few decades. In literature, three prominent definitions of FDs such as Riemann-Liouville, Grünwald-Letnikov (GL) and Caputo definitions have been explored [42], [46] – [49], however,Grünwald-Letnikov derivative method has been most commonly used in signal processing applications due to easy in formulation and low complexity [41], [46], [47]

In this work, to obtain more accurate response in passband with a nearly linear phase response, FD is applied for designing IIR filters. For this purpose, the constraints are imposed to satisfy the desired magnitude response in the passband using fractional derivative.

IV. Design of an IIR Filter With Nearly Linear-Phase Response Using Fractional Derivative

As stated above, design of an IIR filter, defined by (14) is a least square minimization problem, and the possible solution may be computed by first differentiation of (14) w.r.t.band equating it to zero as [39]

and results in conventional solution aswhereandare evaluated in passband as [39]

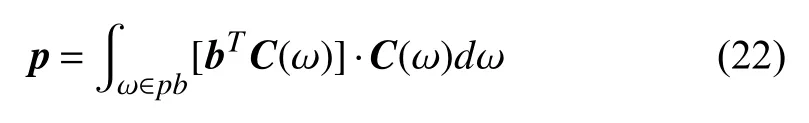
and

From literature review, it evident that an IIR filter with nearly linear-phase response can be designed if the phase error between a delay function and APF is zero in passband region andin stopband region. To satisfy this condition, the following constraints are imposed at the prescribed reference frequency

and

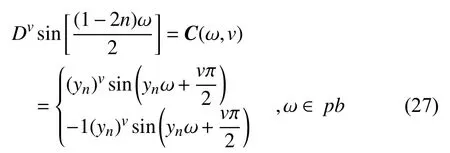
while in stopband region, FD is computed as

where

Now, FDs are evaluated at reference frequencyIfis considered in passband, then (27) is used, otherwise (28) is used for the evaluation. These set of equations are valid for both LPF and HPF, respectively. Let assumeto be in passband region,then the matrixis formulated using (27) as

This equation contains fractional derivatives that have fractional order, therefore, these constraints are also termed as fractional derivative constraints (FDCs). The constraints given by (24) and (31) can be modified as

Thus, this method provides a closed-form solution, and the filter response obtained using the proposed methodology is free from quantization and truncation effect, which is also termed as finite word length (WL) effect, and for this,Tsypskin’s stability criterion [31] is used as

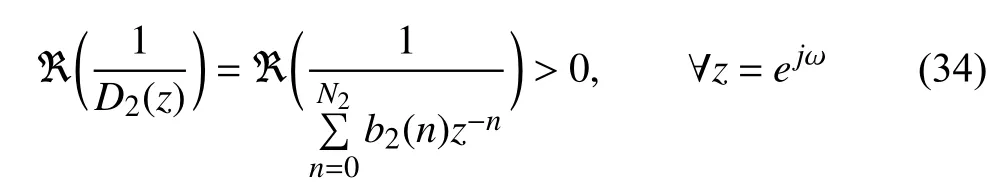
and it is also expressed in term of total unwrapped phase response such that for a LPF as [31]

This condition is automatically satisfied as it is imposed during nearly linear-phase design in proposed method.

V. Proposed Design Method for IIR Filters Based on Fractional Derivatives

As discussed above, designing of an optimal IIR filter is accomplished by designing an APF with the phase response,given by (7) or (8), depending on type of a filter. Degree of design accuracy for respective filters using proposed method is measured by evaluating following attributes, defined as:

and

and for a HPF, these are

A. Design of an IIR Filter Using Single Fractional Derivative Constraint (1-FDC)

In this subsection, designing of a LPF and HPF with different values of a single fractional derivative constraint (1-FDC) is performed. This is accomplished by adopting the values ofandwhich help to keep the slope and concavity of a function intact [39]. However,value of(FDC) is varied from 2.01 to some upper limit ofwhich is decided by series of experiments, and the entire work flow for applying 1-FDC is depicted in Fig. 1. In each experiment, design specifications given by (40) for LPF and(41) for HPF are taken. During the course of designing an IIR filter using 1-FDC, it is seen that the error functionshown in Fig. 2 varies in each simulation, similar to FIR filter design in [39]. Here, Fig. 2(a) illustrate the effect offor a LPF,while Fig. 2(b) for a HPF. It can be seen from the respective figures that variation inis periodic after certain value offor particular value ofIt is also observed thatgets increased after the value ofandfor LPF and HPF, respectively. Therefore, to select an appropriate value of 1-FDCa new greedy based mechanism is proposed, and depicted in Fig. 3 . In each experiment of design, the corresponding fidelity parameters (given in equations from (36)–(39)) are computed and stored. In proposed greedy based method, initially total erroris computed as the sum of passband errorand stopband errorfor all values ofThen, minimum values ofandare sorted out from all the obtained values forand add these values to computeNow, the differenceoffromis computed, and minimum value ofis sorted out. The index corresponding to minimumindicates the best achieved combination ofandfor givenThus, in this way, the best value ofis computed using proposed greedy based technique shown in Fig. 3.

Fig. 1. Flow diagram for execution for design of IIR filter using 1-FD ranging from 2.01 to

Fig. 2. Variation of for different values of (a) for a lowpass filter; (b) for highpass filter.

Fig. 3. A flow diagram for sorting mechanism of optimal value of .

Fig. 4. Flow diagram for execution for design of IIR filter using 2-FD ranging from 2.01 to = 3,4.

B. Design of an IIR Filter Using Two Fractional Derivative Constraints (2-FDCs)

Fig. 5. Variation of for lowpass IIR filter design in case of two fractional derivatives at different (a) = 0.05; (b) = 0.10; (c) = 0.15; (d) =0.20; (e) = 0.25; (f) = 0.30.

Fig. 6. Variation of for highpass IIR filter design in case of two fractional derivatives at different (d)

In order to get more accurate passband response, number of FDCs is increased. In this experiment, an IIR filter is designed with 2-FDCs such thatandwhileandare varying from 2.01 towhereor 4. In each experiment, design specifications given by (40) and (41) are used. The design procedure using the proposed method for 2-FDCs is shown in Fig. 4 , in which fidelity parameters obtained is arranged in a matrix with dimension equal to length of fractional values ofandExploration of 2-FDCs for an IIR filter is an advanced mechanism of 1-FDC, where for each single value ofall the values ofare used for evaluation ofand APF coefficients, with computation complexity ofSimilar to 1-FDC design, the error functionin case of 2-FDCs has a multi-model surface shown in Figs. 5–8. In Fig. 5, variation of the error function obtained in case of a LPF filter for different values of FDCsandand different values of reference frequencyis illustrated, while Figs. 6–8 illustrate error surface of a HPF filter.

It is observed from these figures that the error function is symmetrical around diagonal, corresponding to equal values ofandwhich explains the phenomena of interchangeability ofandSimilar to first experiment, in this case also, a tradeoff betweenandhas been made for sorting the best value of FDCs. Therefore, to obtain the best combination of FDCsa new greedy based search technique is proposed for 2-FDCs, based on the tradeoff between values ofandsuch that both are minimum with highillustrated in Fig. 9. In this technique, firstly suitable offor all individual values ofis sorted out using the mechanism adopted in case of 1-FDC. The outcome of this operation gives the best values of fidelity parameters with suitable value ofThen, same procedure is repeated forThus, the best values of FDsare obtained for optimal design of an IIR filter.

VI. Results and Discussion

In this section, the proposed design procedure using 1 and 2-FDCs is used for designing IIR filters, taking the design specifications given in [31]. For a lowpass filter, these are= [0.0, 0.3],= [0.4, 1.0],= 0.02 dB and= 60 dB and for HPF, these are=[0.5, 1.0],= [0.0, 0.4],= 0.02 dB and= 60 dB.

Fig. 8. Variation of for highpass IIR filter design in case of two fractional derivatives at different (a) = 0.90; (b) = 0.95; (c) = 1.00.

A. Design Examples Based on 1-FDC

A lowpass IIR filter is designed with=[0.0, 0.3],= [0.4, 1.0],= 0.02 dB and= 60 dB using proposed technique based on single FDC. To determine suitable value of 1-FDCproposed greedy based mechanism shown in Fig. 3 is used based on the tradeoff betweenandsuch that the sum of these values has minimum deviation from the sum of minima ofandwhereandare the minimum individual values of passband and stopband errors, obtained for different values ofIn this case, upper value is selected as 14.99, and the total number of samples foris 4799. Similar experiment is repeated for a HPF filter using= [0.5,1.0],= [0.0, 0.4],= 0.02 dB and= 60 dB. In these design examples, reference frequencyis taken in passband region as 0.05, 0.10, 0.15, 0.20 and 0.30 for LPF,whereas in case of HPFis taken as 0.50, to 1.00 with increment of 0.05. The results obtained are summarized in Table I for LPF and Table II for HPF, respectively. The design results obtained are graphically shown in Fig. 10. It is also observed that the fidelity parameter value is not only dependent on suitable value of FDC, however selection ofis also a crucial parameter.

B. Design of LPF/HPF Based on 2-FDC

For more accurate response of a digital filter, number of FDCs is increased. In this case, two-FDCs are exploited. For this purpose, a lowpass IIR filter is designed with14,= [0, 0.3],= [0.4, 1.0],= 0.02 dB and=60 dB using the proposed method discussed in Section V-B.The optimal values of two FDCs, and the fidelity parameters obtained in case of a LPF are summarized in Table III.

TABLE I Performance of Proposed Method for Designing a LPF With and Using 1-FDC

TABLE I Performance of Proposed Method for Designing a LPF With and Using 1-FDC

No. ω0 v3 ep (dB) es (dB) As 1 0.050 6.300 −55.470 −65.242 −43.490 2 0.100 5.120 −63.855 −61.635 −39.950 3 0.150 6.240 −64.502 −67.717 −45.160 4 0.200 3.610 −63.227 −55.086 −33.250 5 0.250 4.300 −60.795 −59.653 −37.350 6 0.300 4.110 −23.675 −43.028 −20.550

Same procedure is repeated for designing a highpass filter with= [0.5, 1.0],= [0.0, 0.4],=0.02 dB and= 60 dB, and the simulations results obtained are tabulated in Table IV . For LPF design, the reference frequency is taken as 0.05, 0.10, 0.15, 0.20 and 0.30, while in case of HPF design, it is 0.50 to 1.00 with increment of 0.05.It is observed that forwithandyields the best combination ofandat the cost of slight decrease in stopband attenuation. The best design results obtained for corresponding FD value are illustrated in Fig. 10.

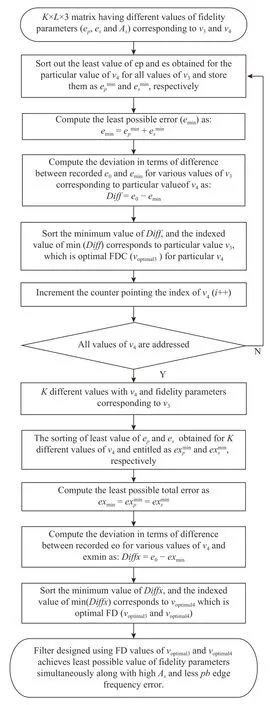
Fig. 9. A flow chart for sorting optimal value of and

C. Comparative Analysis

Based on the experiments conducted for designing of IIR filters using 1-FDC and 2-FDCs, the best performance obtained for IIR filters is summarized in Table V It is evident from this table that the errors in passband and stopband are significantly reduced with slight decrease in stopband attenuation within permissible limit. When compared with eigen filter approach [31], proposed method yield the improved performance in terms of the errors in passband andstopband. The FDCs helps in controlling the passband edge frequency response, which will be beneficial for filter bank design and other signal processing applications. Filter response, and group delay in passband for the best value of FDCs are shown in Figs. 10(a) and (b) for LPF, and Figs.10(c) and (d) for HPF.

TABLE II Performance of Proposed Method for Designing HPF With

TABLE II Performance of Proposed Method for Designing HPF With

No. ω0 v3 ep (dB) es (dB) As 1 0.500 3.840 −50.654 −42.333 −19.999 2 0.550 5.750 −60.974 −56.110 −34.432 3 0.600 4.540 −50.847 −56.897 −35.634 4 0.650 3.990 −56.145 −66.175 −43.995 5 0.700 15.150 −43.556 −69.447 −47.667 6 0.750 9.930 −49.191 −70.179 −47.899 7 0.800 20.870 −44.447 −71.854 −49.132 8 0.850 13.640 −48.813 −71.022 −48.714 9 0.900 12.510 −45.874 −70.591 −48.510 10 0.950 13.280 −44.107 −70.369 −48.476 11 1.000 42.200 −51.408 −56.995 −53.500

TABLE III Performance of Proposed Method for Designing a LPF

TABLE III Performance of Proposed Method for Designing a LPF

No. ω0 v3 v4 ep (dB) es (dB) As 1 0.050 12.310 6.920 −64.398 −60.617 −40.370 2 0.100 2.380 13.870 −63.667 −61.993 −40.520 3 0.150 6.250 12.250 −65.389 −66.634 −44.230 4 0.200 3.400 13.940 −61.036 −57.500 −35.800 5 0.250 13.940 4.300 −61.090 −59.545 −37.280 6 0.300 10.190 4.270 −56.793 −42.691 −20.290

TABLE IV Performance of Proposed Method for Designing a HPF

TABLE IV Performance of Proposed Method for Designing a HPF

No. ω0 v3 v4 ep (dB) es (dB) As 1 0.500 8.720 8.720 −52.735 −53.235 −43.961 2 0.550 3.730 14.060 −60.902 −56.182 −34.489 3 0.600 2.800 6.470 −61.049 −55.644 −35.322 4 0.650 2.010 12.120 −61.928 −63.597 −41.914 5 0.700 6.840 2.330 −61.920 −62.407 −40.992 6 0.750 5.900 3.920 −57.083 −66.873 −44.895 7 0.800 3.530 5.280 −60.246 −64.950 −43.472 8 0.850 3.220 4.710 −64.175 −61.525 −40.417 9 0.900 3.070 5.740 −64.428 −60.198 −39.299 10 0.950 6.550 4.060 −57.936 −63.758 −42.761 11 1.000 2.210 4.380 −58.575 −58.485 −50.027

The proposed method has been also tested for the design of LPF, using same design specifications, given in [51]. It is observed that higher stopband attenuation was obtained in case of iterative algorithm, given in [51], however, anovershoot or spike was obtained at theedge frequency,shown in Fig. 11(a) and this might result in erroneous filtering. While, LPF designed using proposed method has flatresponse with acceptableAnother design example of a LPF is taken from [50], where peak constraint least squares(PCLS) method was used for designing the filter with order =12,= [0.00, 0.50] and= [0.60, 1.00]. When compared with PCLS, the proposed method yields improvement in all three parameters. The proposed method has been also compared with the weighted least squares (WLS) technique[52]. For this, a HPF is designed using order = 14,=[0.525, 1.00] and= [0.00, 0.475], and an improvement inandregion along with increase inis observed. The FDCs helps in controlling the passband edge frequency response, which will be beneficial for filter bank design and other signal processing applications. Magnitude and phase response of designed filter along with the previous state-of-art techniques [50]–[52] is shown in Fig. 11.

TABLE V Filter Performance Analysis and Comparison Using Proposed Methodology

Fig. 10. Frequency response and group delay response of LPF and HPF designed using Eigenvector and proposed method. (a) Frequency response in dB and(b) Group delay in for LPF; (c) Frequency response in dB; and (d) Group delay in for HPF.

D. Computational Complexity

The computational complexity involved for designing an IIR filter using FDCs can be observed from (33). There are two terms involved in computation ofin (33). The first term is a very simplewhich is similar to least square problem solution. Additional computational cost is required for evaluation ofwhereis a null vector. The tedious task is to compute the inverse ofand the size of matrixis ofwhererepresents the total numbers of integral and fractional ordersIn the digital filter design,is usually a small integer ranging from 4 to 5. Therefore, computational complexity required for this matrix is also less, and easy to compute. Therefore, computational complexity involved in the proposed approach is comparatively less, when compared with the techniques given in [50] – [52].

Fig. 11. (a) Magnitude response of LPF obtained by iterative technique [51] and proposed techniques using 1-FDC and 2-FDC; (b) Magnitude response of LPF obtained by PCLS [50] and proposed techniques using 1-FDC and 2-FDC; (c) Magnitude response of HPF obtained by WLS [52] and proposed techniques using 1-FDC and 2-FDC. (The continuous line shows the magnitude response, while dash line represents phase response).

VII. Conclusion

In this paper, a new method has been proposed for the designing of nearly linear-phase IIR filters with improved passband response. An IIR-APF is used with a pure delay function such that both are connected in parallel, and the phase response of an IIR-APF is adjusted for obtaining overall desired magnitude response of LPF or HPF. The main aspect of this method is to find the optimal fractional derivatives with less computation, which are imposed at reference frequency to reduce the phase error between APF and pure delay. An exhaustive simulation performed evidences that FDC based method has multi-modal and symmetrical error behavior.Therefore, in order to find the best FDC values, a greedy based mechanism has been proposed. It is evident from the simulation results that passband error has been improved compared to simple Eigen vector approach with less computation. Further, this work can be extended for more number of FDCs, and also for designing multiplierless IIR filter.