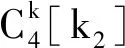正则图字典积的任意幂的无符号和正规拉普拉斯谱
魏 斌, 王维忠
(兰州交通大学 数理学院, 甘肃 兰州 730070)
通过对一些简单的图施加图的运算往往会得到一些较复杂的图。利用参与运算的因子图的参数性质,刻画运算后得到新图的相应性质,是图论中的一种重要方法。2013年,WANG Wei-zhong等[1]给出了正则图经过两种图的一元运算后所得新图的拉普拉斯特征多项式。文献[2]和[3]对广义联图分别刻画了邻接谱与拉普拉斯谱和特征多项式。2014年,WU Bao-feng等[4]刻画了H-联图的无符号拉普拉斯谱和正规拉普拉斯谱。2017年,Abreu等[5]给出了字典积的任意幂的邻接谱和拉普拉斯谱。受上述文献的启发,本文进一步考虑当G和H是正则图时,Hk[G]的无符号拉普拉斯谱和正规拉普拉斯谱。
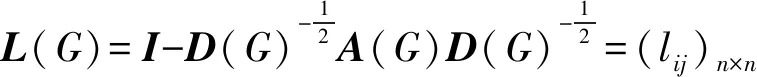
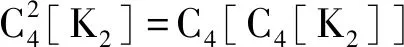
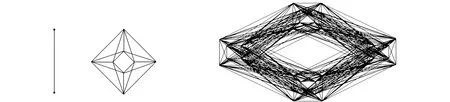
图1 K2和H1[G]=C4[K2] 图
1 预备知识
首先引入一些记号。设方阵M的无符号拉普拉斯谱和正规拉普拉斯谱分别为SpecQ(M)和SpecL(M)。符号a+SpecQ(M)(a+SpecL(M))表示对SpecQ(M)(SpecL(M))中的每个特征值加a;类似地,a·SpecQ(M)(a·SpecL(M))表示对SpecQ(M)(SpecL(M))中的每个特征值乘以a;而符号(SpecQ(M))[n]((SpecL(M)[n])表示对SpecQ(M)(SpecL(M))中的每个特征值的重数乘以n。文中的其他记号和术语参见文献[7-9]。
接下来,给出几个引理。
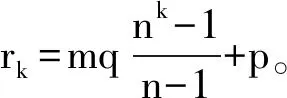
引理2[4]设H和G分别是阶数为n和m的正则连通图,正则度分别为q和p。则
SpecQ(H[G])=(mq+(SpecQ(G){2p}))[n]∪(2p+mSpecQ(H))。
引理3[4]设H和G分别是阶数为n和m的正则连通图,正则度分别为q和p。则
2 主要结果
在这一部分,将给出正则图的字典积的任意幂的无符号拉普拉斯谱和正规拉普拉斯谱。在以下叙述中采用集合并集的传统表示方法来表示多重集的并集,即集合A和集合B中的公共元素在A∪B中出现的次数等于在A和B中出现的次数之和。
2.1 无符号拉普拉斯谱
首先刻画Hk[G](k≥0)的无符号拉普拉斯谱。
定理1 设H和G分别是阶数为n和m的正则连通图,正则度分别为q和p。则
SpecQ(Hk[G])=(A∪B∪C)D,
其中
C=(2rk-1+mnk-1SpecQ(H)),
注1 当k=0时,SpecQ(H0[G])=SpecQ(G)。
证明下面按迭代次数k进行归纳证明。
(ⅰ) 当k=1时,注意到B=∅,由引理2知结论显然成立。
(ⅱ) 假定迭代次数等于k-1时命题依然成立,即
SpecQ(Hk-1[G])=(A1∪B1∪C1)D1,
其中
C1=(2rk-2+mnk-2SpecQ(H)),
则当迭代次数为k时,由Hk[G]的定义及引理2可知
SpecQ(Hk[G])=SpecQ(H[Hk-1[G]])=
(mnk-1q+(SpecQ(Hk-1[G])2rk-1))[n]∪(2rk-1+mnk-1SpecQ(H)),
将SpecQ(Hk-1[G])=(A1∪B1∪C1)D1代入上式可得
(A∪B∪C)D,
从而当迭代次数等于k时,命题依然成立。定理得证。
下面的推论1给出一个正则图与它自身的字典积的任意幂的无符号拉普拉斯谱。事实上,设H是连通的正则图,且H0=K1(孤立点),H1=H,Hk=Hk-1[H](k≥2)。则由定理1立得如下推论。
推论1 设H是n阶q-正则连通图,则Hk的无符号拉普拉斯谱为
SpecQ(Hk)=(A∪B∪C)D,
其中
C=(2rk-1+nk-1SpecQ(H)),
下面给出定理1的一个简单应用。
例1 如图1所示,m=2,n=4,p=1,q=2,则由定理1可知
其中
C=(2rk-1+2×4k-1SpecQ(H)),
特别地,当k=2(如图2所示)时,有
(10,18[4],20[16],22[8],26[2],42)。
2.2 正规拉普拉斯谱
接下来给出Hk[G]的正规拉普拉斯谱。
定理2 设H和G分别是阶数为n和m的正则连通图,正则度分别为q和p。则
其中
注2 当k=0时,SpecL(H0[G])=SpecL(G)。
证明下面仍按迭代次数k进行归纳证明。
(ⅰ) 当k=1时,由引理3知结论显然成立。
(ⅱ) 假定迭代次数等于k-1时命题成立,即
其中
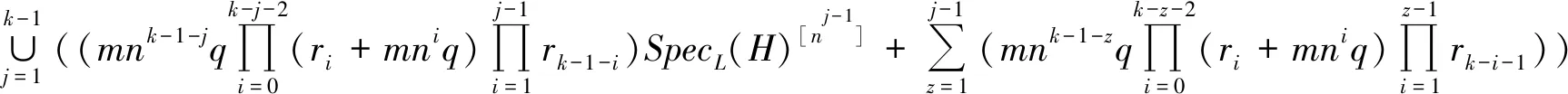
则当迭代次数为k时,由Hk[G]的定义及引理3可知
SpecL(Hk[G])=SpecL(H[Hk-1[G]])=
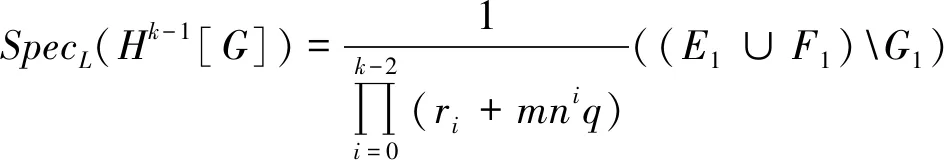
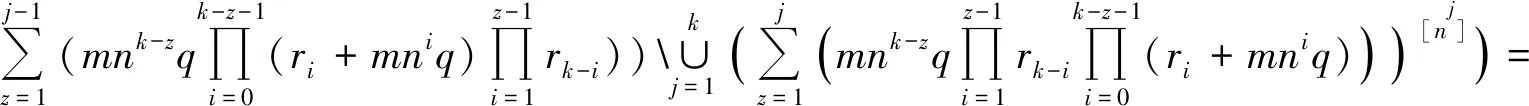
从而当迭代次数等于k时命题依然成立。定理得证。
下面给出一个正则图与它自身的字典积的任意幂的正规拉普拉斯谱。事实上,设H是一个正则图,且H0=K1(孤立点),H1=H,Hk=Hk-1[H](k≥2)。则由定理2立得如下推论。
推论2 设H是n阶q-正则连通图,则
其中
下面给出定理2的一个应用例子。
例2 如图1所示,m=2,n=4,p=1,q=2,则由定理2可知
其中
特别地,当k=2(如图2所示)时有
3 结 语