电动汽车轮毂电机—多连杆悬架系统设计与优化

王冬良，陈 南，秦洪艳

（1.三江学院机械与电气工程学院，江苏 南京 210012；2.东南大学机械工程学院，江苏 南京 211189）

1 引言

电动汽车采用轮毂电机直接驱动方式后，取消了变速器、换档机构和差速器等装置，使传动系统结构简化，提升了车辆的空间利用率、具有较好的动力学特性。若电动汽车依托传统汽车底盘系统运用轮毂电机驱动方式，其在悬架结构上存在前、后轮横向外移等形式的变化。同时，电动汽车装备轮毂电机后，车辆的非簧载质量也随之增加，影响车辆的操纵稳定性、平顺性等性能以及轮胎的磨损。可见，传统车辆的底盘悬架机构已不再适合轮毂电机直驱式电动汽车。因此，设计适用于轮毂电机直驱式电动汽车的悬架系统已是亟需解决的关键技术。

目前，关于车辆悬架系统的运动特性分析及优化，国内外的一些学者已做了大量的研究工作：文献[1]中运用回归分析法分析了麦弗逊式悬架的运动特性；文献[2]中运用轮跳、加载地面制动力和侧向力方法对传统客货两用车辆的双横臂悬架、多连杆悬架进行了运动学分析；文献[3]中运用瞬时轴线理论提出了传统车辆多连杆悬架系统的主动回正控制策略；文献[4-7]中通过ADAMS/Car的仿真模型分析传统车辆多连杆悬架的运动学特性。

通过对传统车辆不同类型悬架特性进行分析，发现传统车辆的多连杆悬架可对车轮全方位控制、以最佳角度和最小支撑力实现悬架机构与车辆定位参数的完美融合，有优越的操纵稳定性和良好的行驶平顺性。

因此，利用传统汽车的多连杆悬架系统，在轮毂内引入轮毂电机，构建一种适用于轮毂电机直驱式电动汽车的轮毂电机-多连杆悬架系统，运用NASG-Ⅱ算法对悬架跳动过程中的电动汽车前轮前束角、外倾角以及轮距变化等目标进行了优化，减小轮胎磨损，提高电动汽车的操纵稳定性。

2 多连杆悬架数学模型的建立

多连杆悬架常有上前连杆、上后连杆、下前连杆、下后连杆、转向横拉杆和减震器组成，如图1所示。

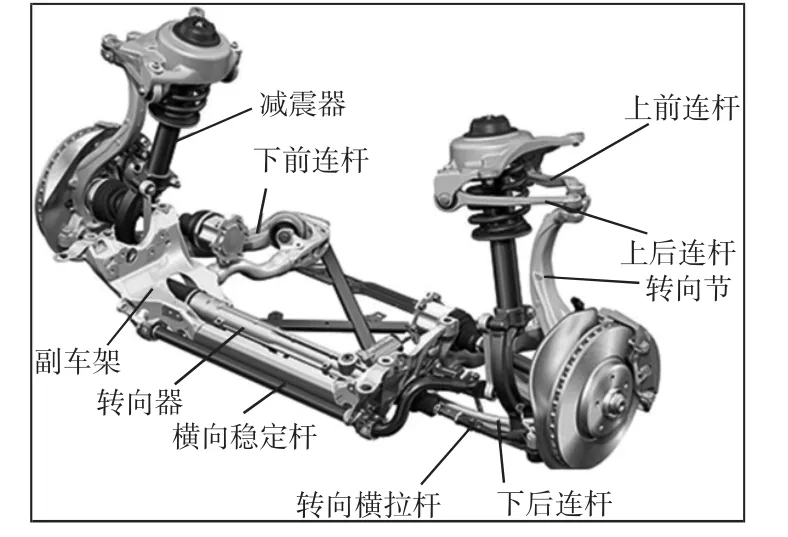
图1 传统车辆的多连杆悬架结构Fig.1 Multi-Link Suspension of the Traditional Vehicle

依据多连杆悬架的特征完成结构简化，其几何模型，如图2所示。主坐标系的原点O位于车辆质心处，x轴的正方向为车辆前进方向，y轴的正方向为指向车辆的左侧，z轴的正方向为指向车辆的上方。Ai为各连杆与副车架的连接点，Bi为各连杆与转向节的连接点，C为车辆的车轮中心。

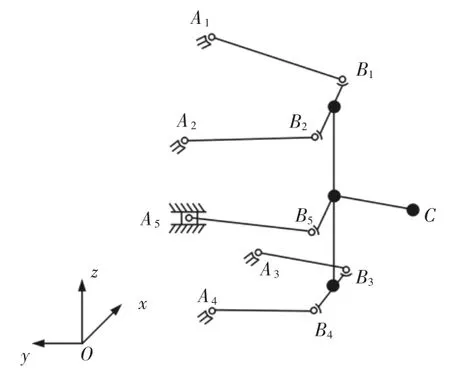
图2 多连杆悬架结构简图Fig.2 Structure Diagram of Multi-Link Suspension

在进行多连杆悬架运动特性分析时，将连杆与转向节、连杆与副车架的运动副连接形式均简化为球面副，则多连杆悬架有2个自由度（即车轮沿z轴的上下跳动、车轮随转向横拉杆的转动）。将转向横拉杆与车身假设为固定，此时，多连杆悬架有6个自由度，其中，5个为各连杆绕自身转动的自由度。因此，车辆悬架的空间姿态由唯一的参数（即车轮中心C沿z轴的上下跳动）来确定。

设车辆转向节绕x、y、z轴转动α、β、γ角，转向节与各连杆的连接点可以通过空间坐标变换矩阵K与车轮中心重合来确定。

转向节空间坐标变换矩阵K为：

其中，cα=cosα，sα=sinα；cβ＝cosβ，sβ=sinβ；cγ＝cosγ，sγ=sinγ；

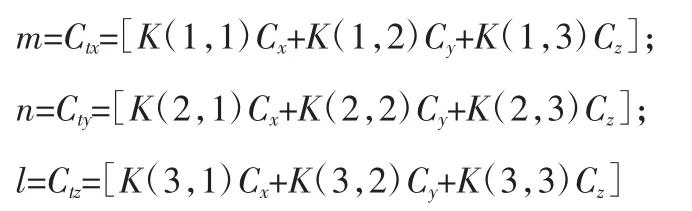
设车轮中心C的z向初始值为C0z，当车轮在上下跳动时，以轮心的z坐标改变量dz为输入，则轮心C运动后的z坐标为：

因此，转向节上的各点应满足：

考虑多连杆悬架的各连杆是刚体，悬架在运动过程中，其长度不变，故：

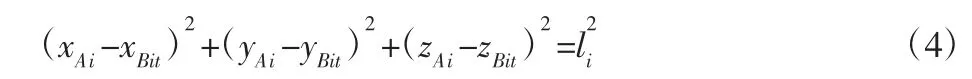
式中：li—连杆长度

xAi、yAi、zAi—Ai的坐标分量；

xBit、yBit、zBit—车轮跳动后Bi的坐标分量。

当车轮处于不同位置时，通过式（3）、式（4）可以求得车轮在跳动后转向节上的各点坐标。转向节空间位置解出后，车轮在上下跳动过程中的外倾角、前束角以及轮距变化量也随之确定。

设车辆车轮平面的法向量为n=［nx，ny，nz］，则多连杆悬架的外倾角αv=arctan（nz/ny），前束角δ=arctan（nx/ny），轮距变化量S=Cty-Cy。

3 多连杆悬架数学模型的验证

在构建轮毂电机-多连杆悬架动力学模型前，先作如下假设：

（1）电动汽车底盘及副车架均为刚体；

（2）电动汽车轮毂、悬架各连杆、转向横拉杆均为刚体；

（3）多连杆悬架中各连杆与副车架、车架及转向节的铰接均为刚性连接。

采用二次瞬时轴线法设计多连杆悬架的虚拟主销轴线，利用ADAMS/Car完成轮毂电机-多连杆悬架运动学仿真模型的构建，如图3所示。

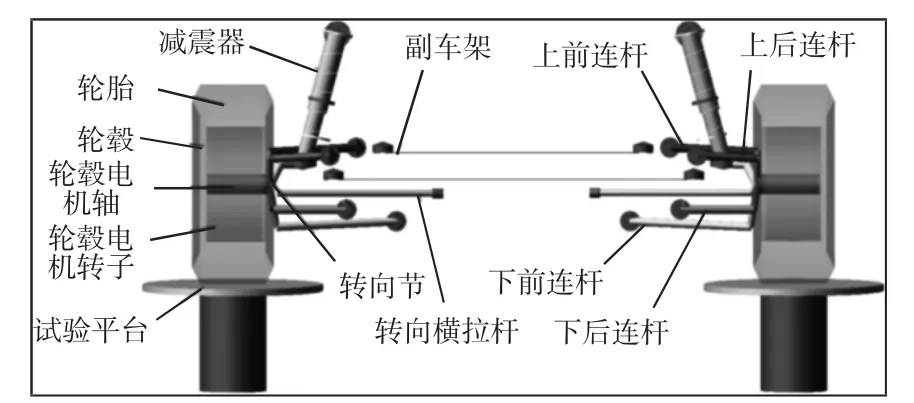
图3 电动汽车轮毂电机—多连杆悬架仿真模型Fig.3 Simulation Model In-Wheel Motor and Multi-Link Suspension for Electric Vehicle

对构建的多连杆悬架模型在ADAMS/Car中进行轮跳运动学仿真分析，采用双轮同向激振仿真，跳动行程为±100mm，将前轮外倾角、前轮前束角和轮距变化量的曲线与数学模型计算结果进行分析，如图4、图5所示。

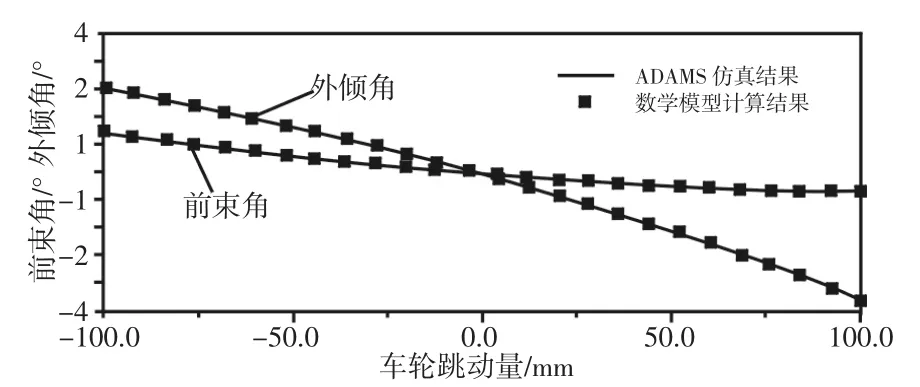
图4 前束角与外倾角的变化对比Fig.4 Comparison of Variation for Toe Angle and Camber Angle

图5 轮距变化量的变化对比Fig.5 Comparison of Variation for Wheel Travel Track

由图可知，两种方式得到的变化规律基本一致，相互得到了验证，也说明所构建的数学模型具有较好的准确性，为后续研究提供保障。

4 悬架灵敏度分析

多连杆悬架的结构硬点参数数量较多，为了节省优化时间，提高优化效率、精度。先对悬架硬点灵敏度分析，先采用单变量灵敏度分析计算出对悬架运动特性影响比较大的硬点，再运用扰动法进行多变量灵敏度分析。选取上前连杆与副车架的连接点A1的z坐标zA1、x坐标xA1，上前连杆与转向节的连接点B1的x坐标xB1，上后连杆与副车架的连接点A2的z坐标zA2、x坐标xA2，上后连杆与转向节的连接点B2的x坐标xB2，下前连杆与转向节的连接点B3的x坐标xB3，下后连杆与转向节的连接点B4的x坐标xB4共8个变量，每个变量的扰动量为（±10）mm，每个变量有5个水平，进行灵敏度分析。变量灵敏度分析结果，如表1所示。表中：“o”—没有影响；“*”—影响非常小；“**”—影响一般；“***”—影响较大。

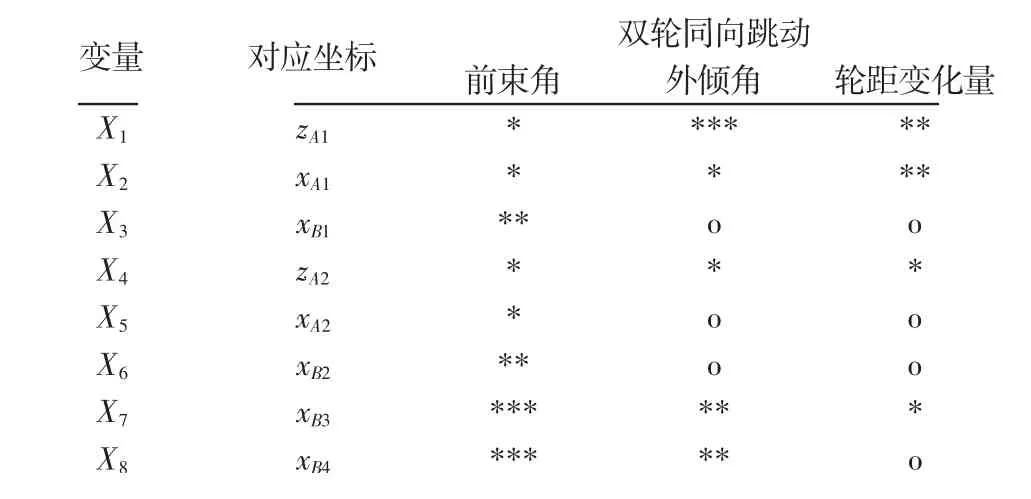
表1 灵敏度分析结果Tab.1 The Corresponding Relation of Optim ization Variables

5 悬架多目标优化

在优化过程中，采用文献[8-10]提出的改进的非支配排序遗传算法（NSGA-II，non-dominated sorting genetic algorithm II），运用精英策略最大限度地保持各优化目标间的独立性、较好的全局寻优能力，大大提高变量的处理能力和鲁棒性。

5.1 基于NSGA-Ⅱ算法的多目标优化

结合多连杆硬点参数，构建多目标优化模型：

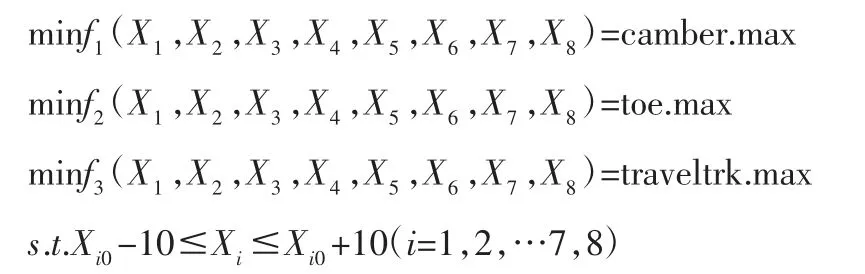
式中：camber.max—悬架在上下跳动过程中，外倾角的最大变化范围；toe.max—悬架在上下跳动过程中，前束角的最大变化范围；traveltrk.max—悬架在上下跳动过程中，轮距变化量的最大变化范围；Xi0指第i变量对应硬点坐标的初始值。

以上述8个变量的坐标值为设计变量，多连杆悬架在轮跳±100mm过程中，对前束角、外倾角和轮距变化量进行多目标优化。

采用的NSGA-Ⅱ算法参数设置：种群规模为400，迭代次数为1000，交叉因子取0.8，变异因子取0.04，得到Pareto最优解集，如图6所示。

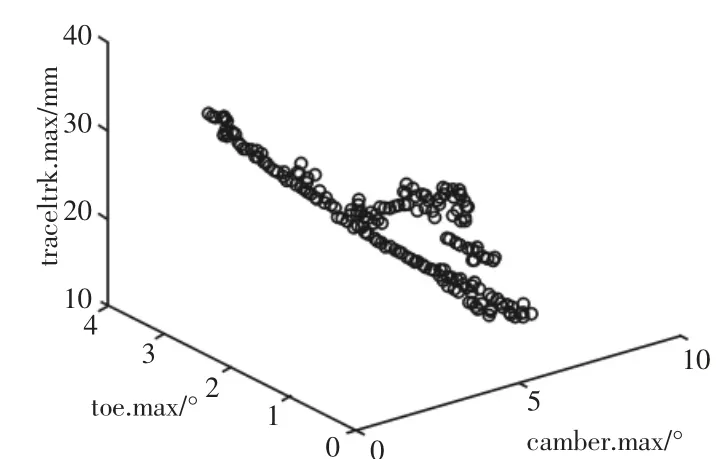
图6 Pareto解集Fig.6 Pareto Solution Set

5.2 优化结果分析

由图6可知，三个优化目标间存在冲突关系，该优化问题有多个解，可根据轮毂电机-多连杆悬架设计的具体要求，选择满足设计要求的外倾角、前束角以及轮距变化量，确定适合的定位参

数[11-14]。

为了验证NSGA-Ⅱ算法的多目标优化效果，选取多连杆悬架优化后的Pareto最优解集所对应的硬点坐标，如表2所示。

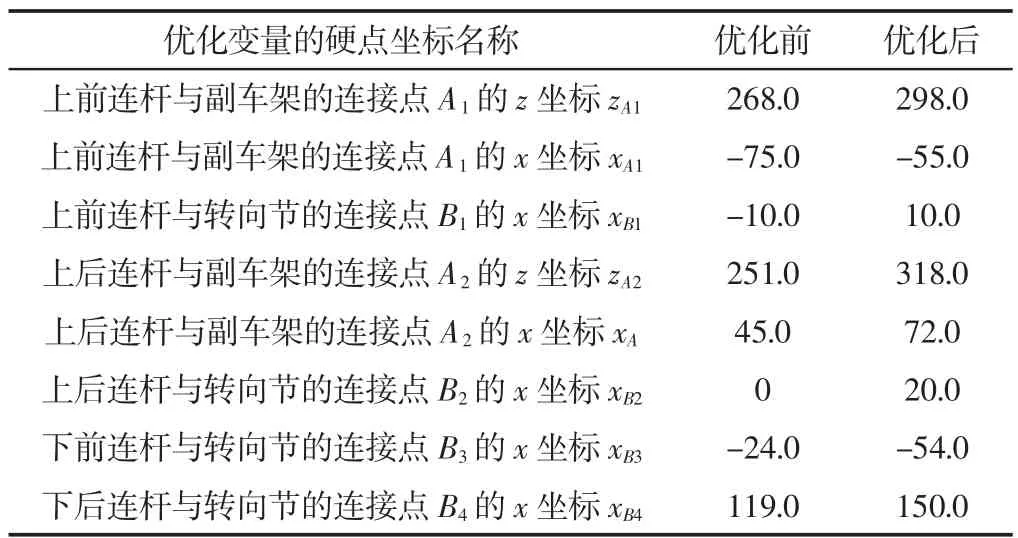
表2 多连杆悬架硬点优化的部分Pareto解集mmTab.2 Pareto Solution Set of Optim ization for Multi-Link Suspension Hard Point（mm）

依据表2中的优化数据，得到优化后的外倾角、前束角以及轮距变化量的曲线，并与优化前的曲线进行对比分析，如图7～图9所示。

图7 优化前后的外倾角曲线对比Fig.7 Camber Angle Curve Contrast Before and After Optimization

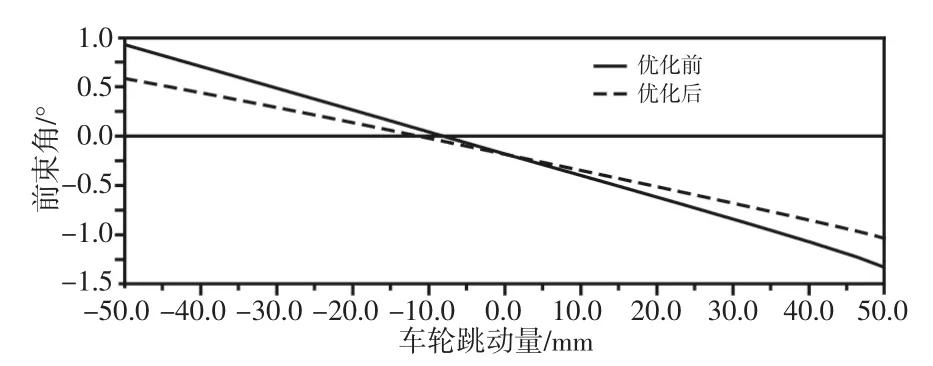
图8 优化前后的前束角曲线对比Fig.8 Toe Angle Curve Contrast Before and After Optimization

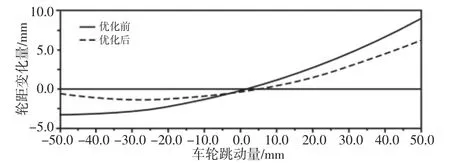
图9 优化前后的前轮距变化量曲线对比Fig.9 Wheel Travel Track Curve Contrast Before and After Optimization

由参数曲线对比可知，在车轮上下跳动过程中外倾角从（1.9°～-4.6°）减至（0.1°～-2.8°），车轮在下落过程中向正方向变化、上跳行程中向负方向变化；车轮在上跳过程中前束值从（-1.35）°变至（-0.9）°，接近弱负前束或零前束，具有转向不足特性、在凹凸路面行驶时具有良好的操纵稳定性；优化后的轮距变化量在±5mm/±50mm内，符合理想的悬架参数的设计要求，同时可以减少轮胎磨损、减少横向偏移现象、提高行驶稳定性。可见，优化后的多连杆悬架运动特性得到了显著地改善。

6 结论

（1）依据传统的多连杆悬架，结合轮毂电机的结构特征，构建了一款适用于轮毂电机驱动的多连杆悬架系统，建立了轮毂电机-多连杆悬架系统的数学模型，确定其外倾角、前束角以及轮距变化量，在ADMAS/Car构建了运动学模型，对其进行轮跳运动学仿真分析，并结果与数学模型的计算结果基本一致，相互得到了印证。

（2）基于构建的悬架模型，结合改进的非支配排序遗传算法NSGA-Ⅱ，提出了一种能解决轮毂电机-多连杆悬架系统多目标优化的有效方法。

（3）运用NSGA-Ⅱ对多连杆悬架的定位参数进行优化分析，得到了优化目标的Pareto最优解集。由优化结果可知：优化后的悬架运动特性得到了显著改善，NSGA-Ⅱ算法对直驱式电动汽车悬架系统设计具有指导意义，降低设计成本、缩短研发周期。