基于改进Apriori算法的客户需求数据分析方法

张 雷，董万富，阚欢迎，赵希坤

（合肥工业大学机械工程学院，安徽 合肥 230009）

1 引言

随着企业的竞争逐渐从“以产值为中心”过渡到“以客户需求为中心”[1]，产品的设计是否能够满足客户需求，决定着产品在市场竞争中的成功与否。企业赢得市场的关键在于对客户购买产品时会着重考虑的一些问题进行快速响应，对产品进行客户需求分析，将需求信息转化为产品功能设计点，从而有效地指导产品设计，使设计出的产品更能满足客户需求，提高客户满意度。从企业的角度，对客户需求数据进行分析，可节约产品的开发周期、成本和资源，推动产品结构和功能的改进，同时有利于发掘潜在客户，提高产品市场占有率；对产品消费者而言，可以使设计出的产品更能符合消费者的真实需求，满足用户的使用习惯和经验，有利于提高客户使用产品的舒适度和满意度。这就要求企业对客户需求信息进行分析，从而能够对不断变化的客户需求进行有效预测，将所得信息反馈到产品的设计制造端，对产品结构和功能进行改进，尽可能设计制造出满足客户需求的产品。

文献[2]提出一种改进的BASS模型，用于短生命周期产品需求预测中历史数据缺乏、需求影响因素考虑不充分导致的预测精度较低等问题；文献[3]通过构建大规模定制环境下客户需求信息的分类模型，采用框架法和非结构化对客户需求信息进行解释；文献[4]在建立客户需求与可配置产品模块实例之间的映射关系的基础上进行模块化产品优化配置设计；文献[5]提出了一种结合群体决策、多格式偏好分析以及最小二乘模型的客户需求分析方法；文献[6]基于模糊集理论和欧几里德空间距离，提出了一种客户需求权重计算方法；文献[7]提出了一种基于模糊卡诺模型的客户需求分类和权重评价方法，使客户需求类别与相关重要度计算相结合的客户需求预测方法；在以数据驱动的产品设计方面，文献[8]提出了一种基于时间依赖的产品使用数据分析的集成设计改进方法；文献[9]提出一种基于强化学习的数据驱动的浮选工业过程操作最优控制；文献[10]提出了一种动力数据驱动用于热声学稳定运行的低预混式混合动力装置的设计，这些只考虑到了产品使用过程，没有把客户需求考虑到产品的设计中去。

通过以上文献的分析，在客户需求和数据驱动的产品设计方面，国内外学者做了很多研究性工作，并且取得了较多成果和广泛的应用，但并没有考虑把客户需求信息和产品使用性能情况以及产品更新换代时结构功能改进方面综合起来应用到产品的设计制造中，因此提出了一种基于改进的Apriori算法对客户需求数据进行综合分析，并通过冰箱产品的客户需求为例，说明该方法的实施过程。

2 Apriori算法的改进

2.1 Apriori算法介绍

Apriori算法是关联规则中最具影响的挖掘频繁项集的经典算法[11]，该算法的基本思想是首先对数据库事务中的项目进行扫描，获取这些项目组成项集的支持度值，其次判断这些项集的支持度与设定的最小支持度的关系，保留大于或等于设定支持度的所有频繁项集，若项集的支持度小于设定的支持度时，使用剪枝的方法将该项集去除。该方法先找出频繁1项集所组成的集合L1，然后用L1去寻找满足设定支持度的频繁2项集的集合L2，以此类推，使用迭代的方式去逐层搜索满足条件的频繁项集，直到搜索不到满足设定支持度的更高维度的频繁K项集为止，该算法的流程，如图1所示。

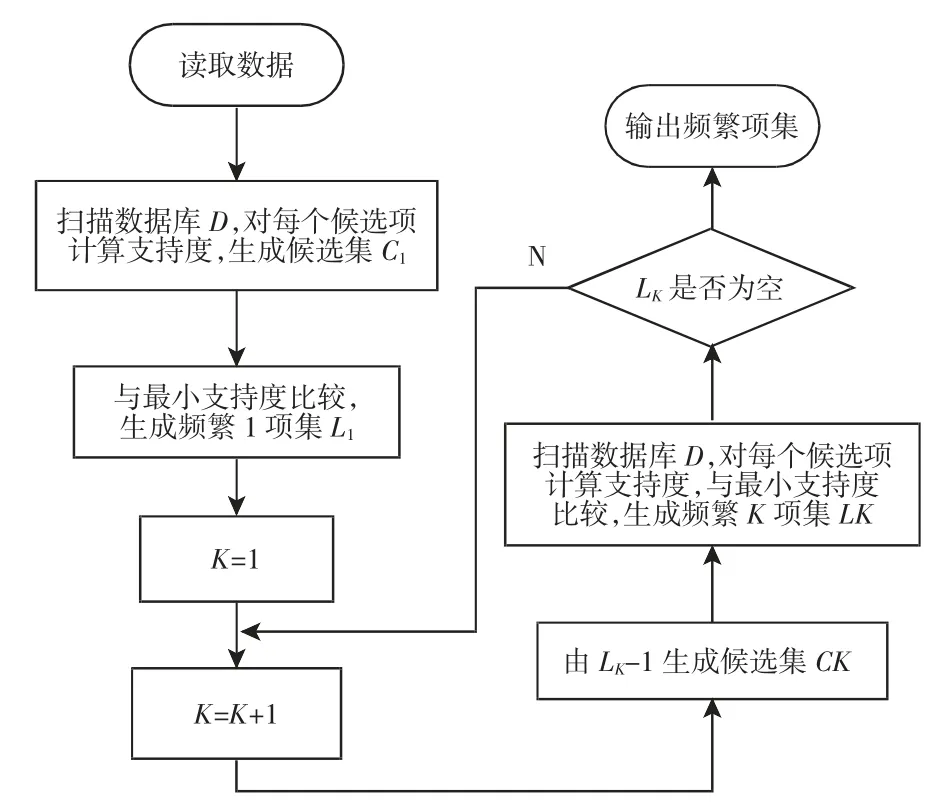
图1 Apriori算法流程图Fig.1 Apriori Algorithm Flowchart

但是该算法在每次寻找频繁K项集的集合Lk时都需要扫描整个数据库，该算法的缺陷也是很显然的：（1）当数据量很大时，由低维度的频繁项集连接生成高维度的候选频繁项集的数量非常大；（2）每次验证候选频繁项集时，都需要扫描整个数据库，非常耗时。

2.2 布尔矩阵介绍

布尔矩阵是元素只取0或1的矩阵[12]，使用布尔矩阵可以有效地替代数据中的事务数据项，并且可以使数据的存储空间得到很大程度的优化。设X=｛x1，x2，…，xm｝，Y=｛y1，y2，…，ym｝，R为从X到Y的二元关系，记rij=R（xi，yj），R=［rij］m×n，则R为布尔矩阵。

若有k个元素存在事件A中，则称A为k项集事件，A中满足设定支持度的事件称为频繁项集，算法可行性主要依据布尔矩阵下面的2条性质：（1）当布尔矩阵每列中1的个数即该项出现的次数不满足设定的支持度时，该列为非频繁项集，依据频繁项集的反单调性，该列可以被去除；（2）当布尔矩阵每行中1出现的次数小于k时，意味着数据项中的项数小于k个，不能满足频繁k项集的产生，故在求频繁k项集时可以被去除。

2.3 改进Apriori算法

针对上述Apriori算法存在的两个明显缺陷，利用布尔矩阵对其进行改进，改进后的算法在数据库扫描时只需扫描一次，通过扫描事务数据库映射成的布尔矩阵相应的列就能得到项的频度，其中布尔矩阵的行和列分别代表数据项和事务项，通过事务数据库映射成的布尔矩阵就可以进行频繁项集的查找。

由数据库D映射成的布尔矩阵的第一行是表志位，该行中的元素r1j为1时，表示第j列所代表的事务是候选频繁项集，r1j为0时，表示第j列所代表的事务不是候选频繁项集。首先我们对布尔矩阵进行初始化，令矩阵中第一行所有的元素r1j=1，表示算法在第一次执行剪枝时，所有的事务项都是候选频繁项集。其中r1j（r1j≥2）表示事务中Ti-1项事务出现的情况，若r1j=1时，表示该位置所代表的Ti-1事务项被选择，r1j=0时，表示该位置所代表的Ti-1事务项未被选择。对于一个给定的数据库D的列中出现的数字序号表示该事务数据库中记录的数据项，数据库D的行中出现的I1，I2，…，In表示数据库中每项事务的被选择情况，若布尔矩阵中的元素r1j（r1j≥2）为1时，表示序号为Ti-1的行中Ij所代表的事务项被选择，反之则表示序号为Ti-1的行中Ij所代表的事务项未被选择。对事务数据库做一次完整的扫描后，就可以把事务数据库D在f：D→R的方式下映射成布尔矩阵R。

3 客户需求数据分析

3.1 客户需求数据的获取

随着科技的进步，可以很便捷的获取客户需求数据信息。从客户信息反馈、参考相似企业产品、相关专利和科技文献等途径采集客户需求信息，社交媒体等为人们提供了在虚拟社区和网络互动，为人们分享和交流信息和意见提供方便，利用社交媒体可以通过设置在线调查问卷的方式进行客户需求数据信息的获取，也可以通过发放调查问卷的方式获取客户需求数据信息。

3.2 客户需求数据分析方法

对于事务数据库D映射成的布尔矩阵中的每一项（列）Ij的方向向量用表示，则Ij的支持度support=r2j+r3j+…+r（m+1）j，对于R中任意不同的两项（列）Ii、Ij的逻辑运算表示为：Rij=Ri∩Rj=（r2i∩r2j，r3i∩r3j，…，r（m+1）i∩r（m+1）j），其中∩表示逻辑“与”运算符，则Ii∩Ij的支持度support=r2i∩r2j+r3i∩r3j+…+r（m+1）i∩r（m+1）j，在寻找候选频繁K项集时的逻辑运算如下：Rij…k=Ri∩Rj∩…∩RK=（r2i∩r2j∩…∩r2k，r3i∩r3j∩…∩r3k，…，r（m+1）i∩r（m+1）j∩…∩r（m+1）k），所以K项集的支持度为：support=r22∩r23∩…∩r2k+r3i∩r3j∩…∩r3k+…+r（m+10）i∩r（m+1）j∩…∩r（m+1）k利用布尔矩阵改进的Aprori算法寻找频繁k项集的步骤如下：

（1）扫描事务数据库D，并把事物数据库D映射成布尔矩阵R（根据事务数据库事务数为m，项目数为n，将事务数据库映射成（m+1）行，n列的布尔矩阵。并初始化第一行都为1）；（2）设定事务数据库D的最小支持度min_support；（3）计算每个项目的支持度support=r2n+r3n+…+r（m+1）n，如果In＜min_support则r1n=0，得到了频繁1项集，构成新的布尔矩阵R1；（4）将得到的布尔矩阵R1按照逻辑运算计算支持度，将支持度大于或等于min_support的项保留，则得到频繁2项集，并将非频繁项集的标志值改为0，得到R2；（5）使用递归的方法，通过频繁K项集计算出频繁（K+1）项集，并将非频繁项集的标志位改为0，得到布尔矩阵Rk；（6）当（k+1）的频繁项集的最大支持度maxsupport＜min_support，输出频繁K项集，否则转入Step5继续寻找更高维度的频繁项集。

利用布尔矩阵改进Apriori算法的流程，如图2所示。

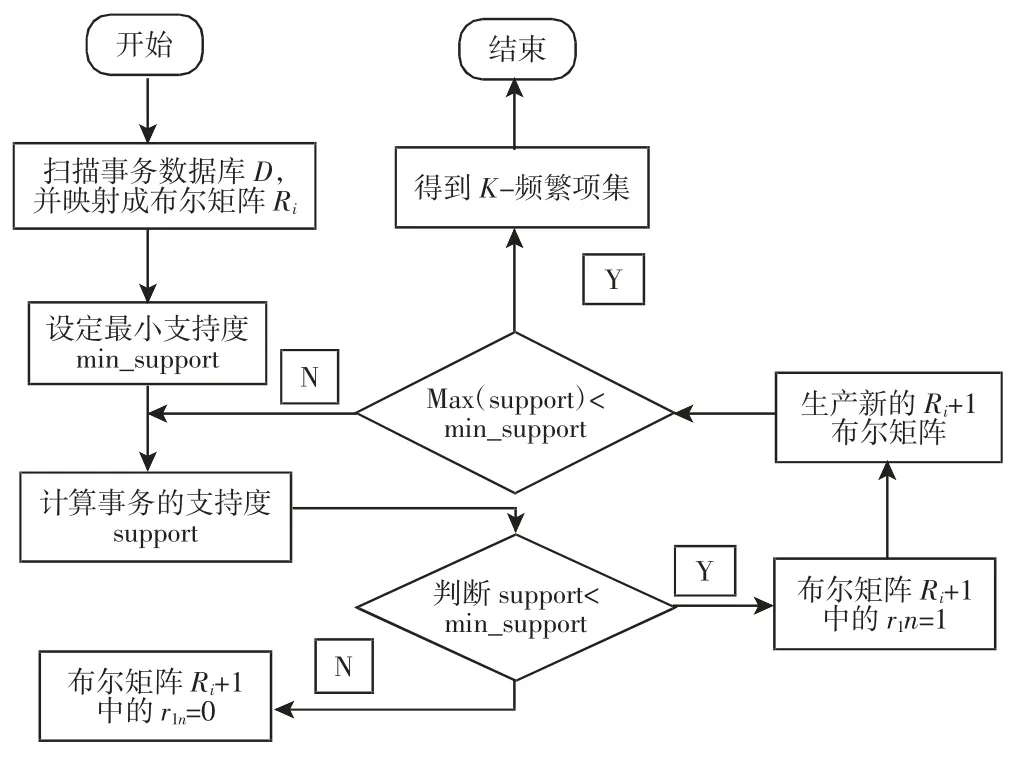
图2 利用布尔矩阵对Apriori改进算法流程图Fig.2 Using Boolean Matrix to Improve the Flow Chart of Apriori Algorithm

3.3 算法评估

采用布尔矩阵改进的Apriori算法的计算复杂度远比改进前Apriori算法的复杂度低，改进前的Apriori的复杂度为其中D为数据库事务数量，K为频繁项集的大小。改进后的算法的复杂度为O（m·nk），其中m为事物数据库事务数，n为项目数，K为频繁项集的大小，由于每次获得K频繁项集时，非频繁项集的标志位都会被修改，元素被修改成0的标志位，将不再参与寻找（K+1）频繁项集的运算，m为寻找K频繁项集时修改后的数据库事务的列数，很显然K值越大m值越小。并且引入布尔矩阵后的运算都是逻辑运算，计算速度也有提升，所以改进后的算法在时间复杂度上更优，同时也节省了很大的I/O资源，同时降低了计算的空间复杂度。与改进前用大量重复字符存储事务数据相比，改进后的算法，把事务数据库映射成布尔矩阵来存储，在每次寻找频繁项集时都不用开辟新的空间来存储非频繁项集。因此在具有很大数据量的事务数据库的存储方面节省了大量的存储空间。

4 案例分析

以某企业针对冰箱产品开展的客户需求调查为例，按性别、年龄段（18～30岁、30～40岁、40～50、50岁以上）、地区（A地区、B地区、C地区、D地区），地区的划分依据该企业冰箱产品市场占有率排名前四的地区，把客户分类，并结合正交实验的思想从调查问卷数据库中抽样出16组数据，利用改进的Apriori算法对客户需求数据进行分析，说明该方法的具体实施过程，挖掘得到客户需求数据之间深层次、不确定性的联系，为产品的设计制造提供参考依据，生产出以数据驱动、市场需求为导向的产品。从客户需求数据库D中抽样出来的客户需求信息，如表1所示。

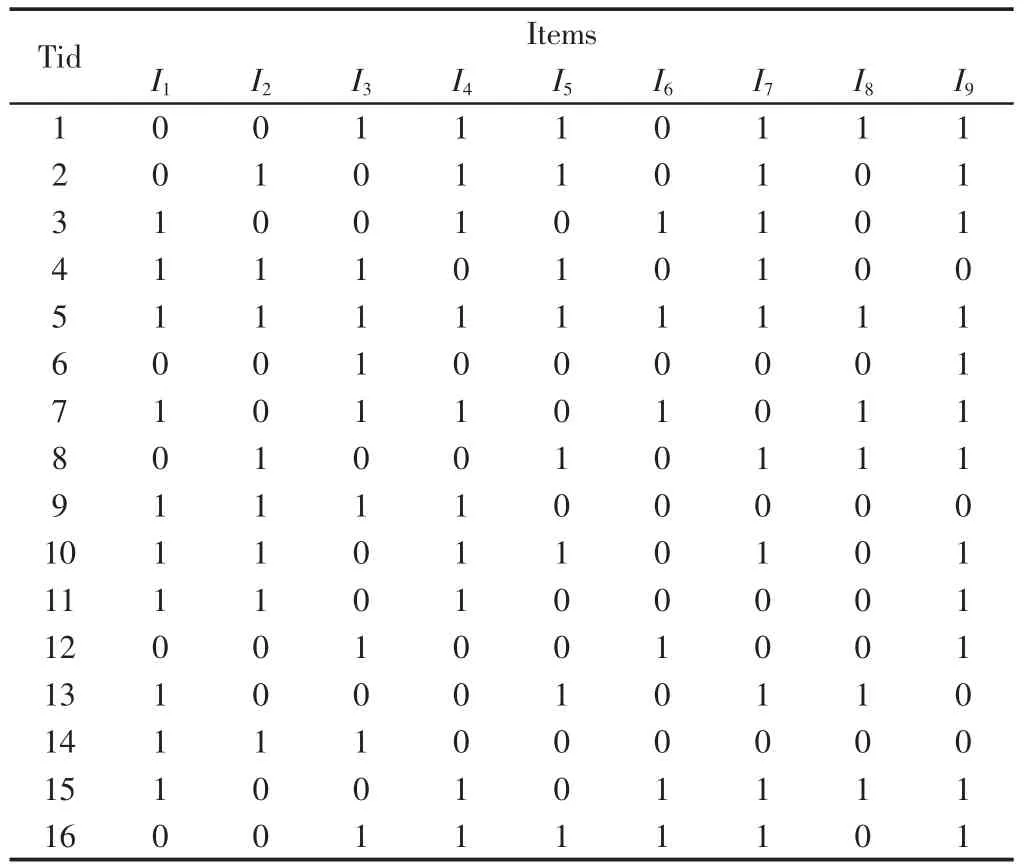
表1 客户需求信息采集Tab.1 The Tem plate of Customer Requirement Gathering

表中：I1—品牌；I2—外观及内饰；I3—价格；I4—耗电量；I5—无异味或不串味；I6—容积；I7—保鲜效果；I8—烹饪教学；I9—营养分析。

利用布尔矩阵改进的Apriori算法进行分析，步骤如下：

（1）扫描事务数据库D（客户需求信息采集表），在f：D→R的方式下映射成布尔矩阵R，如下所示：

（2）设定事务数据库D的最小支持度min_sopport=3。

（3）计算候选频繁1项集，得I1=10，I2=8，I3=9，I4=10，I5=9，I6=6，I7=10，I8=6，I9=12所以1频繁项集为｛I1，I2，I3，I4，I5，I6，I7，I8，I9｝，表示在最小支持度为3时，得到的1频繁项集。

（4）计算候选频繁2项集，得I12=6，I13=5，I14=7，I15=5，I16=4，I17=6，I18=4，I19=6，I23=4，I24=5，I25=5，I26=1，I27=5，I28=2，I29=5，I34=5，I35=4，I36=4，I37=4，I38=3，I39=6，I45=6，I46=5，I47=7，I48=4，I49=9，I56=3，I57=9，I58=4，I59=7，I67=4，I68=3，I69=6，I78=5，I79=8，I89=5其中Iij表示在满足最小支持度时，得到的2频繁项集为：｛I12，I13，I14，I16，I17，I18，I19，I23，I24，I25，I27，I29，I34，I35，I36，I37，I38，I39，I45，I46，I47，I48，I49，I57，I58，I59，I67，I68，I69，I78，I49，I89｝根据频繁项集的性质，产生非频繁项集的标志位所在列的序号为2，所以r12=0。得到新的布尔矩阵R1：

由矩阵R1可得非频繁项集的表志位所在列的序号为2，则第二列将不再参与后续频繁项集的寻找运算。鉴于篇幅限制以及计算的复杂度，采用Matlab编程进行频繁项集的寻找计算，得I4579=5，因为不存在5频繁项集，所以事务数据库的频繁项集为I4579。计算结果表明，在抽取的16组客户需求数据中，客户在购买产品时，会着重考虑冰箱产品的耗电量，使用过程中是否有异味或串味情况，冰箱的保鲜效果以及是否具有对储存在冰箱中的食材具有营养分析的功能。

5 结论

利用布尔矩阵改进的Apriori算法，很大程度上降低了计算的复杂度，使计算速度有了很大的提升，把事务数据库转化为布尔矩阵来存储，在具有大数据量的存储方面节省了大量的存储空间。对获取的调查数据进行分析，由计算结果可知，顾客在购买冰箱时，会着重考虑冰箱在使用过程中的耗电量，这也反映出客户的绿色消费观念的提高，更加注重低碳生活，在使用过程中是否会出现异味、串味情况以及冰箱在使用过程中的保鲜效果也成为顾客关心的重要问题，用户在使用冰箱的过程中着重考虑上述问题的同时也更加注重冰箱的智能性，希望冰箱具备对储存食物具有营养分析功能。通过以上分析可知，在冰箱的设计制造过程中要更加注重冰箱的能耗问题，设计出更加绿色、节能、低碳的产品，通过技术创新在冰箱结构设计和工艺方法方面尽量解决或降低冰箱在使用过程中出现的异味、串味问题以及提高冰箱在使用过程中的保鲜效果，同时在冰箱的设计制造时考虑冰箱的智能化。