永磁同步电机新型降阶磁链观测器设计

毕长飞

（辽宁地质工程职业学院机电系，辽宁 丹东 118008）

1 引言

针对目前比较常用的永磁同步电机（Permanentmagnetsynchronousmotor，PMSM）矢量控制而言，为了获得较好的PMSM驱动系统调速性能和动态品质，转子位置信息的准确获得必不可少。然而，传统的机械位置传感器的安装会导致系统安装成本的增加和尺寸的增大[1-2]。无位置传感器技术的出现和发展可以说在一定程度上解决了机械传感器所存在的缺点，伴随着现代制造工艺的不断提高和PMSM优越性能，PMSM应用场合也愈来愈多，因此设计一种高性能无传感器控制技术显得尤为重要。

虽然无传感器控制技术近年来得到了快速的发展，但目前诸多控制算法仍然是基于PMSM的基波数学模型中与转速和位置信息有关的变量，并采用不同的观测器方法在线实时估计，为矢量控制提供所需要的位置信息和转速信息。文献[3-5]采用模型参考自适应算法进行转子位置估计，该方法估计精度的核心是估计位置偏差的准确性，虽然数学模型是精确的，但估计精度仍然要受电机参数变化的影响，同时要受电流检测精度的影响。文献[6-8]采用滑模观测器方法进行转子位置在线估计，然而采用滑模观测器得到的估计变量中含有高频的切换信号，虽然可采用低通滤波进行处理，但通常会引起相位的滞后。文献[9-10]采用磁链积分法，计算简单动态响应快，但该方法存在直流偏移问题，且没有误差校正环节。文献[11]采用全阶Luenberger观测器设计无传感器控制算法，计算量大且不容易实现。为了获得较好的控制性能，提出了一种基于降阶磁链观测器算法的转子位置和转速信息估计方法，该方法采用α-β静止坐标系下的PMSM数学模型，应用Luenberger观测器设计方法，并接PI锁相环技术，通过理论分析和仿真验证证明了观测器的正确性。

2 永磁同步电机的数学模型

静止坐标系下PMSM的数学方程可以表示为[12]：

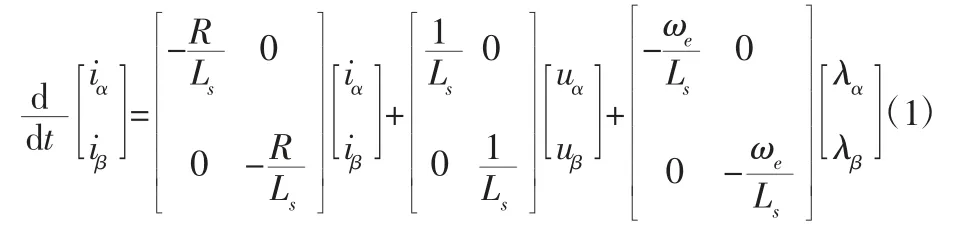
式中：d/d t—微分算子；［uαuβ］T—α-β轴系下的电压；［iαiβ］T—αβ轴系下的电流；ωe—电角速度；R、Ls分为定子电阻和电感；［λαλβ］T—永磁体磁链λ在α-β轴系下的映射，即，且满足。

为了便于观测器的设计，将［λαλβ］T作为扰动状态变量。并定义扩展状态量x为x=［x1x2x3x4］T=［iαiβλαλβ］T，将α-β静止坐标系下的电压分量作为输入量u，即u=［u1u2］T=［uαuβ］T，将电电流分量定义为输出量y，即y=［y1y2］T=［iαiβ］T。

此时，PMSM的状态方程可以表示为：

3 降阶磁链观测器设计

由于式（2）中的变量［iαiβ］T是可测量的，而变量［λαλβ］T是不可测量的。为了得到［λαλβ］T，设计降阶状态观测器为：

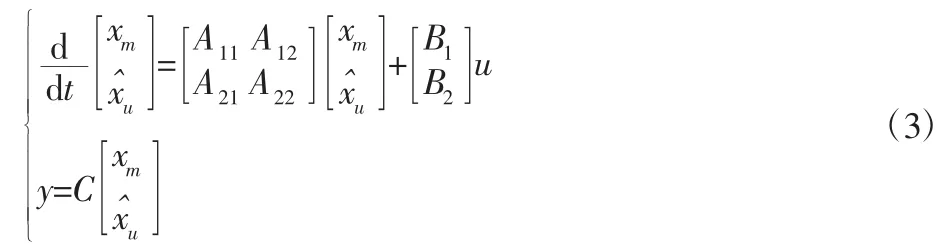
经过变换，式（3）给出了一般状态观测器的表达式，根据降阶状态观测器的控制原理和设计方法[13]，构建PMSM的降阶磁链观测器为：

然而，当电机转速ωe接近零时，D、H、F和G将不能得到有效的解。为了避免此问题，选择观测器中的参数，此时观测器（4）的矩阵变量将变为：

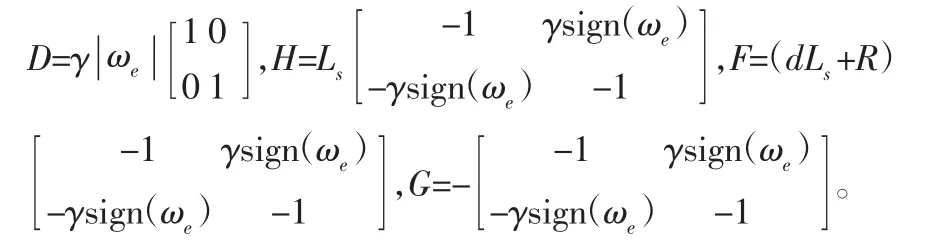
通过上述理论分析，采用降阶磁链观测器方法可以在线估计磁链的数值。为了获得电机的转子位置信息和转速信息，可以根据磁链和转子位置的关系进行获得。

4 转速及转子位置估算

为了获得转子位置信息，通常根据磁链表达式与转子位置之间的关系，利用反正切函数直接计算，即θ^e=arctan（λ^β/λ^α）。虽然该方法计算简单且利于实现，但该方法会引入不必要的噪声信号污染，从而影响转子位置信息的准确性。为了解决此问题，文中设计了一种基于PI锁相环技术的位置估计算法，具体控制框图，如图1所示。

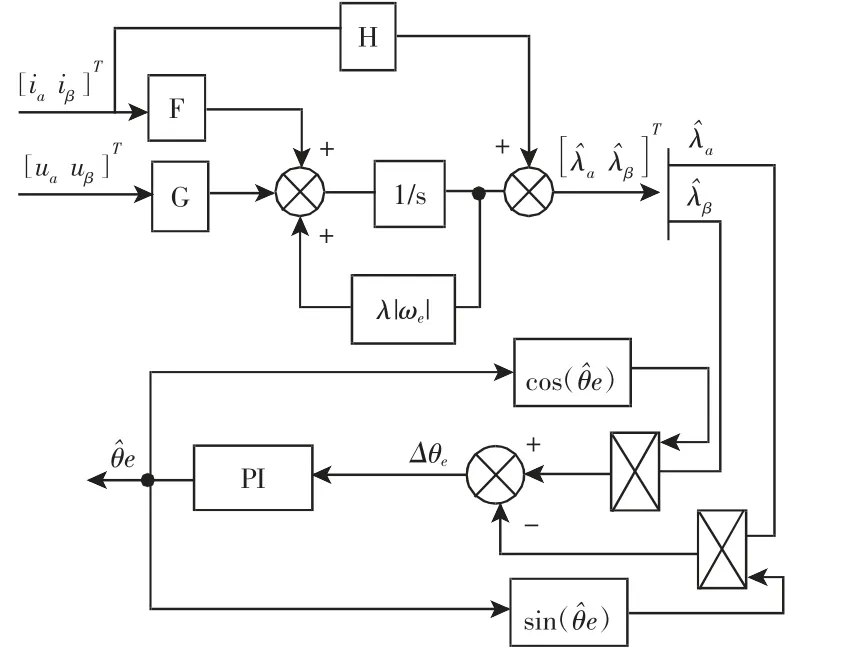
图1 基于PI锁相环技术和降阶磁链观测器的控制框图Fig.1 PI-Based Phase-Locked Loop Technology and Reduced-Order Flux Observer Control Block Diagram

对图1中的Δθe进行归一化处理，可以得到如下表达式：

根据PI锁相环技术的基本工作原理，ω^e和θ^e计算表达式可以采用式（6）表示，即：

式中：ki，kp—锁相环的设计参数。

根据式（6）可以看出，当Δθe非常小时，此时θ^e与Δθe近似相等，即θ^e≈θe，可线性化为：

由式（7）可知，θ^e与θe的传递函数为：

另外，为了设计锁相环的参数，令式（8）的特征方程s2+kps+ki=0的两个负实极点重合在-ρ，则kp=2ρ，ki=ρ2。

另外，锁相环系统的极点ρ由下式决定[12]：

式中：Δθemax—最大观测误差量，该数值可以根据实际系统进行设置。

对于式（9）而言，选择Δθemax相对较小的数值可获得较好的效果，通常选为Δθemax=10°。

5 仿真验证

基于Matlab/Simulink仿真软件可以很好的验证所提算法的可行性和有效性，并为实际系统的开发奠定理论基础。采用的控制框图搭建PMSM驱动系统的仿真模型，如图2所示。其中电机参数为：电阻R=0.96Ω，定子电感Ls=5.25mH、极对数pn=4，转动惯量J=0.0006kg·m2，永磁体磁链为0.183Wb。

5.1 稳态性能分析

为了说明所谓新型降阶磁链观测器的控制性能，首先对电机从静止到稳态运行的过程进行仿真分析，且此时不考虑负载的影响，即设置负载转矩为0。仿真结果可发现，转速估计值能够快速跟踪实际值，且转速误差较小，转速误差为0，如图3所示。另外，电机的转子位置估计值也能快速的跟踪转子位置实际值，说明所提算法从静止到稳态运行的过程具有较好的控制性能。

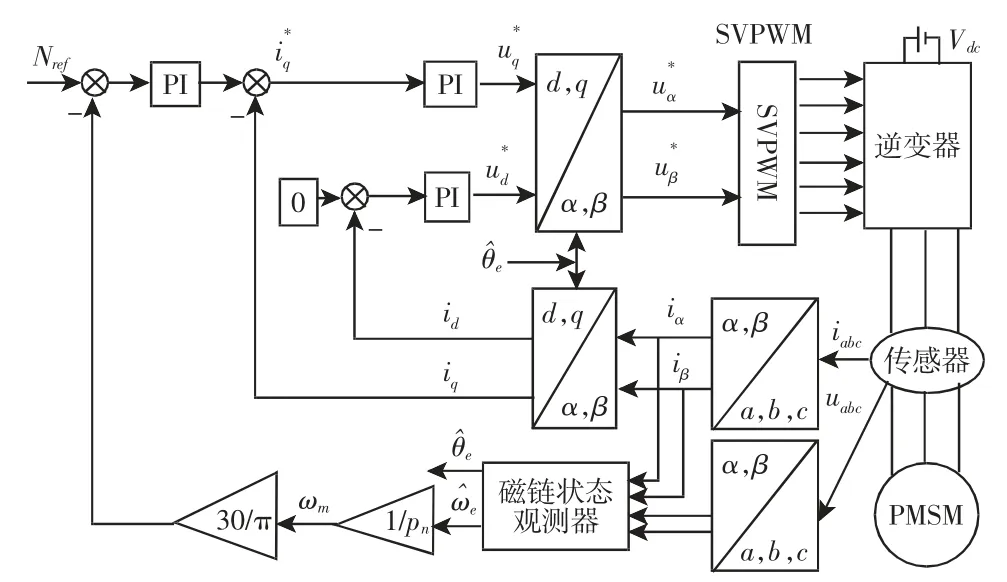
图2 PMSM降阶磁链观测器算法的控制实现框图Fig.2 PMSM Reduced Order Flux Observer Algorithm Control Block Diagram

图3 PMSM从静止到稳态的仿真结果Fig.3 PMSM from Static to Steady-State Simulation Result

5.2 动态性能分析

为了进一步验证当外界条件变化时所提控制策略的鲁棒特性，当电机转速由初始值600r/min突变为1200r/min时的仿真结果，如图4所示。从图4（a）和图4（b）中可看出，电机的转速和转子位置估计值能够快速跟踪上实际值，且估计误差非常小，基本上为0。同时从图4（c）可以看出，当电机转速突变时，转子磁链的估计值能够迅速做出响应，从而可以说明说明电机的动态性能良好。

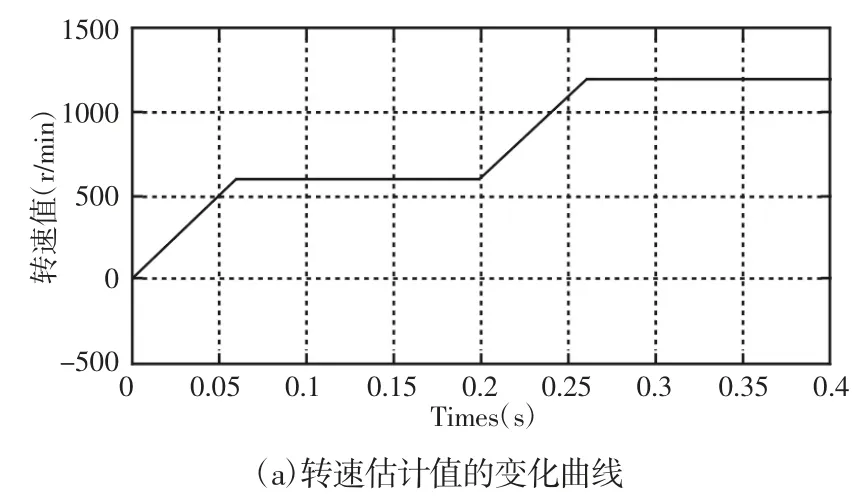
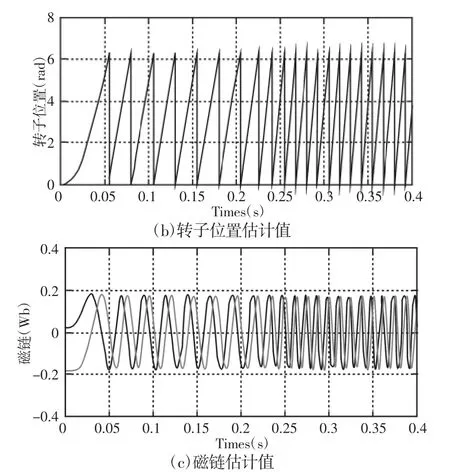
图4 PMSM转速突变时的仿真结果Fig.4 PMSM Mutation Speed Simulation Result

为了进一步验证所提控制策略的抗负载扰动能力，当电机突加负载的仿真结果，如图5所示。当电机在t=0.2s突加负载时，电机的转速和转子位置估计值能够快速跟踪上实际值，且估计误差非常小，基本上为0。从而说明电机的鲁棒性能优越，可以较好处理外界环境和负载条件的变化。

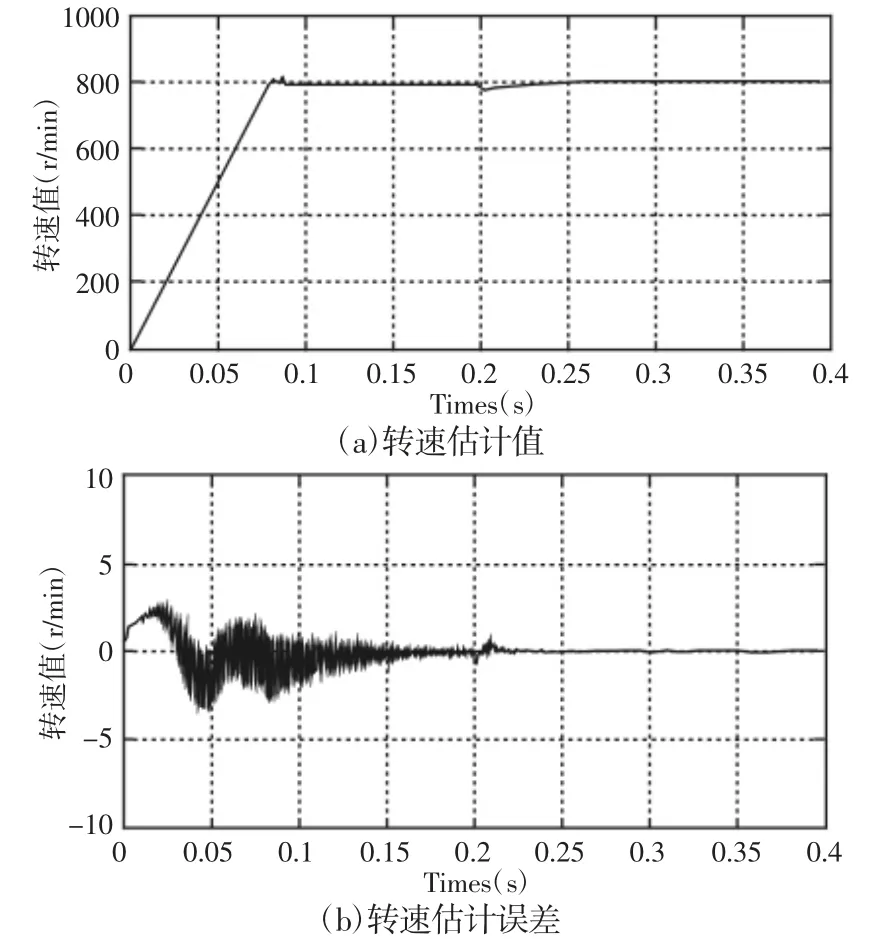
图5 PMSM突加负载时的仿真结果Fig.5 PMSM Sudden Load Simulation Result

6 结论

（1）针对永磁同步电机静止坐标系下的数学模型，基于Luenberger观测器方法的降阶磁链观测器算法，通过使用降阶状态观测器来在线估计转子磁链，该方法与电机参数无关且结构简单，便于实现。（2）为了提高转子位置和转速信息的估计精度，设计了一种基于PI锁相环的新型降阶磁链观测器算法，并给出了详细的参数计算和性能分析。理论分析和仿真结果证明了所提控制算法的优越性能。