马尔科夫聚类改进敏感信息自动监测

杜军龙，周剑涛，王 磊

（江西省信息中心，江西 南昌 330036）

1 引言

互联网技术的发展和应用普及给社会生活的各个领域带来了很大的便利。但由于互联网自组织网络各节点的运行是开放及可以随时进出通信网络，导致网线的拓扑结构会出现较大的时变，同时开放的通信网络中还需要传输与保存各种数据，因此数据安全问题就变得越来越重要，可及时发现隐藏的异常状态，辅助相关人员快速了解网络当前异常，做出正确的判断，解决网络中出现的异常问题[1-2]。网络异常节点及其行为是监测网络数据是否安全的必要条件。异常行为的出现通伴有区别于正常通信信息的敏感信息，通过对这些波动进行异常检测，可以有效的发现异常情况并定位异常节点，在无线传感器网络的实际应用中具有非常重要的意义对于提高网络安全具有十分重要的作用[3]。

国内外学者在敏感信息检测方面主要基于节点信息的时间关联性，该方法在异常检测中有着较高的准确率，但难以找到将信号与网络拓扑结构关联的数学模型，而数据流统计模型难以事先获得[4]。基于统计学的方法具有较高的异常节点和敏感信息检测效率，但需要根据网络的先验信息购建统计模型[5]。机器学习、统计分析及信号处理是用于网络异常节点信息的监测的常用三大类方法，但这些方法虽然能够一定的监测效果，但对异常节点流识别能力有待提高[6]。临近节点检测法[7]根据数相似度或距离来识别敏感信息或判断异常节点，但算法复杂度较高，且无法监测连续异常节点。

聚类方法在无需统计模型的情况下即可对当前网络数据异常信息监测处理[8]。马尔科夫聚类是基于马尔科夫过程的经典的快速图聚类方法，其图聚类，可以在不进行聚类预估的情况下实现数据聚类[8]。为此，基于美国的Ablience骨干网数据，采集通信网络的流数据构建流连接结构，基于网络流连接结构，利用敏感词距离信息对网络节点的行为分别进行聚类，根据聚类差异情况实现敏感信息的监测及相应异常节点的有效区分实验验证算法的有效性。

2 网络敏感信息分析

2.1 通信网络模型

Ablience骨干网的网络拓扑结构，如图1所示。该网络共有9个节点，每个节点布设一个专用路由器，各个节点均遵从具备网络监测功能的Netflow协议。基于该网络监测协议，每隔4min进行数据采集，数据采样速率为196。Netflow协议数据是通信网络异常信息监测的数据来源。然而实际监测过程中，系统自动采集的数据量很大，且存在很多冗余信息，因此需要对数据进行筛选，以提高数据精准度和降低网络监测的计算复杂度。经过大量测试，由Netflow协议数据中选取了能够代表通信网络信息的9个关键属性，具体为：网络数据包数量、网络层的总字节数、源IP地址、目的IP地址、TCP协议控制标志、下一跳IP地址、传输层源端口号、传输层目的端口号和协议类型。

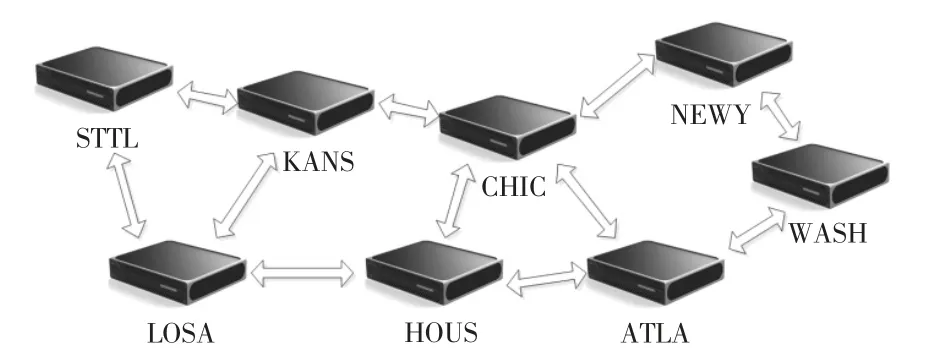
图1 Ablience骨干网结构图Fig.1AblienceBackboneNetworkStructure

2.2 敏感信息距离计算

通信网络中的攻击异常及产生的敏感信息较多，文中主要分析通信网络中最为常见的扫描异常和拒绝服务两种攻击异常信息，并通过敏感信息间距离描述其在通讯网络中的位置，敏感信息距离T（t1，t2）计算式为：

式中：pt1、pt2—敏感信息在通信网络中的双亲节点函数；l（pt1）—节点在网络中所在的层数；pt1fpt2—两节点存在祖先与后代关系；pit1=pjt1-i，j—两节点共有相同父节点；ptc—与t1或t2具有相同父节点的元素节点。

多敏感信息之间的网络距离为各敏感信息距离各，即：

通过计算各异常节点产生的敏感信息之间的距离，可以较为准确的反映敏感信息的分布情况，敏感信息中的敏感词距离越小表明敏感信息越集中，即当前信息的敏感程度越高；当敏感词距离越大，说明敏感信息节点越分散，即当前信息和敏感程度越低[6]，因此，利用敏感词间的距离信息对通信网络的节点行为分别进行聚类，根据聚类差异情况可以实现敏感信息的自动监测及其对应异常节点的有效区分。

3 马尔科夫聚类改进敏感信息监测

马尔科夫聚类（Markovclusteralgorithm，MCL）的关键主要是图扩展和膨胀两个过程[10]，都是对状态转移矩阵进行操作，通过不断的扩展和膨胀最终使得图邻接矩阵满足收敛条件。扩展是模拟转移矩阵的随机漫游，首先，在网络邻接矩阵中增加一条自环；然后，对邻接矩阵进行幂运算。取正整数，对图邻接矩阵自乘e次，得到新的进行了e步转移的状态转移矩阵。膨胀操作是矩阵进行规则化的过程，完成邻接矩阵的各列进行规则化，其处理公式为：

式中：M—图邻接矩阵；k—矩阵M行数；M*—规则化后的矩阵；

τ—矩阵膨胀操作的松弛系数；p、q—矩阵的行和列下标。

膨胀操作能够实现节点概率的自适应调整，即不断增加概率较大节点的概率，同时也不断减小概率较小节点的概率。经过马尔科夫聚类后，邻接矩阵的各个节点与其他节点均会连接成正值的边，且和为1。

马尔科夫聚类后，达成稳定状态的邻接矩阵是监测通信网络状态的关键。如果存有异常，邻接矩阵的聚类中心及其数量会出现变化。为此，基于马尔科夫聚类，构建了异常节点及其产生的敏感信息的监测算法，算法以邻接矩阵描述预处理后提取的网络流图并进行马尔科夫聚类，然后从聚类结果中判断敏感信息。

3.1 邻接矩阵及敏感度计算

网络数据流经过预处理得出网络流图后，对流图中的各个节点进行编号，形成一个索引二维矩阵。如果网络流图中有N个节点，则矩阵行列数均为N。如果网络流图中源节点和目的节点存有连接关系，则其邻接矩阵值非零，且值越大，邻接关系就越密切，反之为零值。

设J（ti）为敏感信息中敏感词的结构相关性，则基于词间距离的敏感词间结构相关度为：

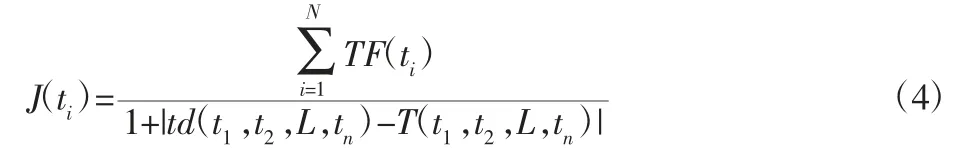
式中：J（ti）—网络中敏感信息ti的总词数：td（ti）—词间距，td（ti）与T（ti）之间的差值绝对值越小，对应的信息数据越符合最初始结构关系，对应的敏感度值越大。

基于敏感词敏感度得到敏感信息的相关度为：

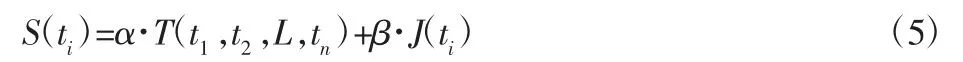
其中，α、β满足α+β=1。

3.2 马尔科夫聚类

邻接矩阵构建完成后，对邻接矩阵添加自循环边，设置扩展和膨胀的幂次参数α和e，进行马尔科夫聚类，直至满足预设置稳定条件。

传统MCL算法通过迭代得目标函数最小实现图最优分割，进行聚类和计算隶属度，但其存在样本特征未优化导致细节易丢失和空间结构关系不能很好表达导致对噪声误聚类两个主要缺点，为此，在敏感信息词间距离和敏感度计算基础上，采用核空间MCL算法，引入核函数，在高维映射空间通过模糊聚类分析扩展MCL算法；引入马尔可夫随机模型，对邻接图局部特征建模，以有效利用像素结构信息。

核空间MCL算法的目标函数为：

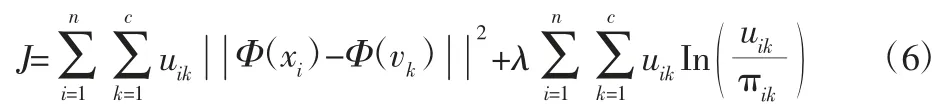
式中：πik—先验概率；Φ（·）—非线性映射；c—聚类数，xi邻接图元素值；vk—输入空间的聚类中心数；uik—隶属度，Σuik=1，λ—加权指数。采用满足Mercer条件的高斯核函数，则有K（xi，xj）=exp（-（2σ2）-1||xi-xj||2），从而得到：

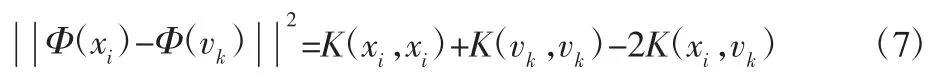
采用拉格朗日乘子可以得到隶属度的迭代式为：

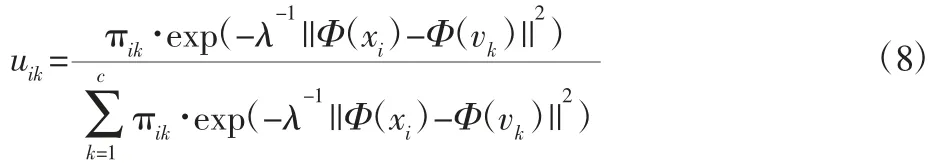
判断邻接矩阵是否达到稳定条件的方式是当再次进行扩展和膨胀操作，邻接概率矩阵不再变化。此时，提取邻接矩阵中的各行正数值，形成一个类簇。如果通信网络中存有异常，邻接矩阵中的行值和列值均相同，此时即可导出IP编号中对应的索引值。

3.3 敏感信息监测识别

网络流图能够有效表示网络流信息的连接关系，当存在异常时，流图的结构参数会随之出现异常，从而识别出敏感信息，进而实现网络攻击的监测。选取网络流图的平均度、最大连通子图比和最大度数比作为识别网络异常的特征。

平均度[7]能够有效表示网络流图的连接状态，通常情况下，网络流图连接越复杂，网络流图的平均度就越大，反之亦然。最大连通子图比[3]能够有效表示网络流图节点之间的是否存在连通，连通性越好，最大连通子图比值就越大。在通信网络敏感信息监测过程中，如果最大连通子图比值较大，则说明网络中的存有访问率较高的傀儡机，或网络中存有病毒。最大度数比[9]也是评价网络流图的重要参数，最大度数比的值越高，通信网络中存有异常信息的概率就越大，一旦最大度数比值接近1，则网络中存有异常攻击。

4 实验结果与分析

以网络采集的实测数据对文中算法监测性能进行测试，实验测试了算法的识别准确性，实验数据为LANL数据集[9]的flows数据，LANL数据集是2010年由Los实验室成员在其内部网络采集，其flows数据共有426045096条数据记录，12027个主机节点，99 433条有效通信边，对数据集中添加拒绝服务攻击，然后利用马尔科夫聚类判断流图节点的聚类变化，聚类前后的网络流图，如图2所示。对比图2（a）和图2（b）可知，聚类前后，簇数和节点数分别增加和减少了一个，并且聚类后展现出了十分明显的全连接关系，这是典型的拒绝服务攻击的特征。这是由于当攻击者向通信网络发起拒绝服务攻击时，被攻击者控制的傀儡机会像服务器发起非常具有规律性的数据，且数据的大小非常相似，因此经过马尔科夫聚类后才会出现良好的全连接关系，且聚类簇数增加一个。

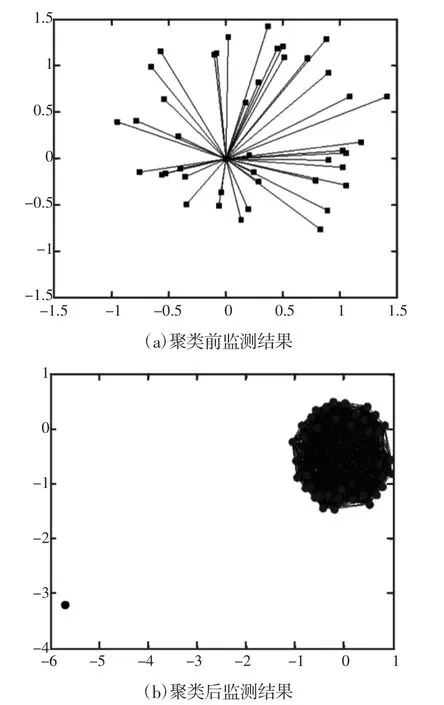
图2 拒绝服务攻击马尔科夫聚类结果Fig.2 Denial of Service Attack Markov Clustering Results

MIT实验室在IDS评测时采集的DARPA 2000数据集[10]，具有较强的权威性和代表性，在数据集中添加网络扫描攻击，提取数据集的络数据流后，利用马尔科夫聚类处理邻接矩阵，聚类前的网络流图结构，如图3（a）所示。经过马尔科夫聚类后，通信网络流图的聚类结果，如图3（b）所示。对比图3（a）和图3（b）可知，经过马尔科夫聚类后，核心聚类结构数据节点有所减少，且与图2（b）同样展现出了良好的全连接状态，这非常符合网络扫描攻击的特征。这是由于当攻击者发起扫描攻击时，会向服务器单方面传送请求数据，但不会服务回应任何信息。为此，经过图聚类算法后，攻击者的请求数据会被聚为一类，且这些数据由于具有较高的相似性而展现出良好的全连接特点。

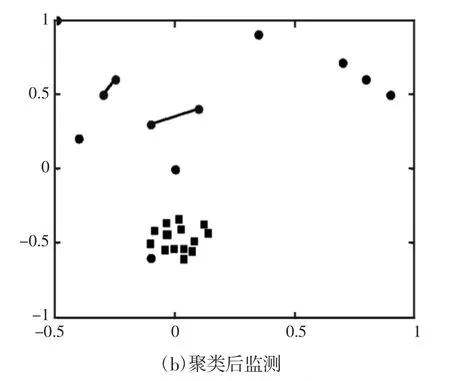
图3 扫描攻击马尔科夫聚类结果Fig.3 Scanning Attack Markov Clustering Results

5 结论

网络敏感信息监测是辅助通信网络发现网络攻击行为的有效途径，针对此问题，提出了基于马尔可夫聚类的自动监测算法，算法利用通信网络数据构建能够表征网络状态的流图，据此构建邻接概率矩阵，然后对其进行马尔科夫聚类以判断聚类前后节点变化，自动监测和识别敏感信息，测试结果验证了算法对网络敏感信息监测的有效性和准确性。