凸轮磨削的动态速度优化方法研究

隋 振，徐 峰，苏振东

（吉林大学通信工程学院，吉林 长春 130022）

1 引言

凸轮作为汽车内燃机的主要机械零件之一，数控凸轮磨削的加工精度直接影响了汽车引擎的动态性能。而传统的凸轮、曲轴等高档磨削加工设备与控制算法一直被国外少数公司所垄断，已经成为制约我国汽车工业发展的重大问题[1]。在数控领域中为了追求凸轮磨削过程中高精度与高效率，国内外学者进行了大量的研究。文献[2]提出了通过几何误差补偿技术提高磨削精度。文献[3]通过研究磨削机理来研究砂轮与进给速度对加工精度的影响。文献[4]利用切点跟踪磨削法对磨削过程行进了误差分析。

磨削速度与加速度作为影响加工精度的主要条件之一，在不改变现有结构的条件下，通过磨削速度优化以减小轮廓误差的方法较易实现。文献[5]利用遗传算法，实现了加工速度的优化。文献[6]推导证明了磨削加工速度与加速度与凸轮加工轮廓误差之间的数学关系，通过同步速度滞后的方法来提高轮廓精度。

文献[7]通过研究当量磨削厚度和切削力的变化规律，给出了数控补偿的计算公式与修正模型。由于凸轮的数控加工过程中为重复进行的磨削过程，文献[8]提出了一种基于CTC的控制理念，将每次的磨削过程看成一个周期，利用上一个周期误差指导下一个周期来达到优化的目的。

基于上述文献，得出了这里的优化方法。主要步骤为：以准恒线速度磨削为基础速度，将前一个磨削周期产生的当量磨削厚度误差利用优化模型求取补偿量，结合遗传算法重新求取优化速度，实现动态优化。

2 恒磨削当量模型

2.1 瞬心法的凸轮切削方程计算

在实际加工过程中，凸轮轮廓是由机床旋转轴和砂轮进给轴联动配合形成的。根据瞬心法来建立凸轮磨削运动模型。速度顺心法凸轮磨削示意图，如图1所示。

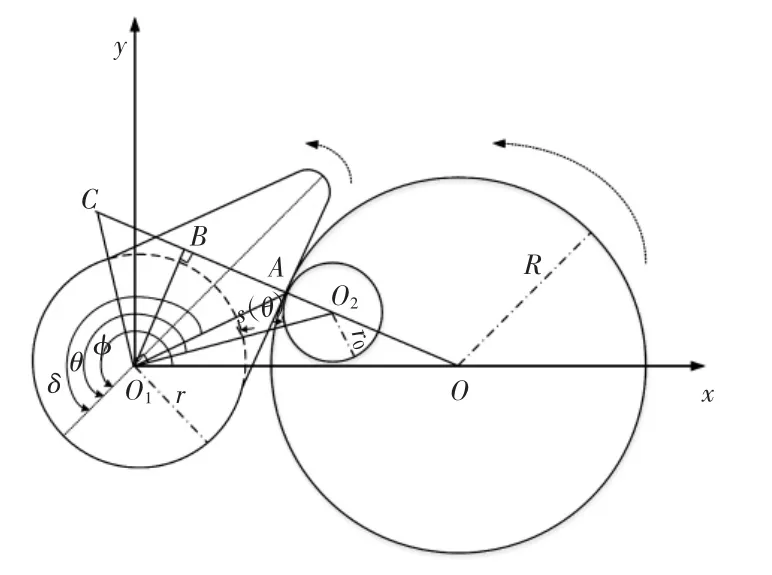
图1 速度瞬心法凸轮磨削示意图Fig.1 Grinding Sketch of Cam With Speed Instantaneous Center Method

图中：O1—凸轮基圆圆心；r—凸轮基圆半径；R—砂轮半径；O—圆心；r0—滚子半径；O2—滚子圆心。凸轮磨削起点从基圆的中心点，且凸轮转过的角度为φ；在磨削过程中砂轮中心点位移表示为X；设A点为实际切削过程中的某一点，则切削点极坐标为ρ=O1A，其对应角度为δ；凸轮滚子对应的角度为θ，且已知凸轮升程曲线可表示为H（θ）。由于A点为实际切削点，则进给砂轮与凸轮在A点应该相切，所以过凸轮圆心O1做直线O1B⊥OO2于点B，又做O1C⊥O1O2于点C。根据做相关辅助线求得凸轮片与挺杆之间的速度瞬心点为C点。通过相关推导后得到凸轮工件旋转转角度为：

进给轴水平方向位移为：

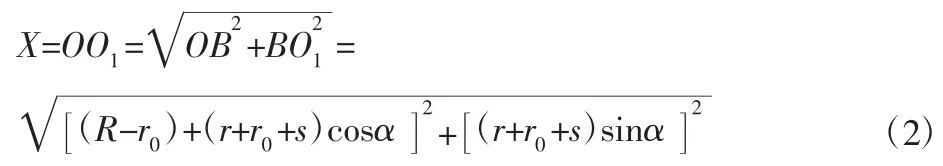
2.2 准恒线速度凸轮磨削求解

当量磨削厚度是控制磨削质量的基本参数，该参数与磨削力和表面粗糙度都有一定的相关。为了使得凸轮工件能获得较好的精度与表面质量，在磨削过程中尽量使得当量磨削厚度值恒定。

磨削当量公式为：

式中：heq—当量磨削厚度；

Q—单位磨削量；

Vs—砂轮线速度；

ap—砂轮磨削厚度；

Vq—了工件磨削线速度。

在不考虑切削深度ap变化的情况下，当量磨削厚度只与砂轮转速和凸轮工件转速相关。实际磨削过程中，砂轮转速远远大于凸轮工件转速，且旋转速度一般为定值，在这种条件下是当量磨削厚度只与凸轮工件的旋转速度相关。

如图1所示，在磨削过程中磨削点A的微动量为d s，则A点的磨削速度Vq可表示为：

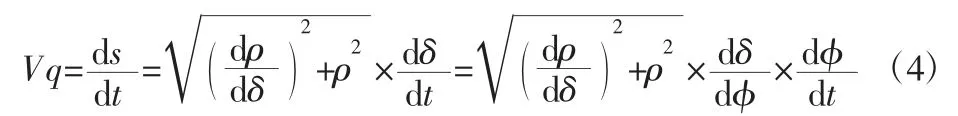
为了方便优化，假设凸轮在基圆磨削过程中角速度恒定为ωi，基圆半径为r，则可求取切削点时的砂轮旋转角速度为：

此时通过调节凸轮工件旋转速度，达到基本的速度优化。凸轮磨削数控系统在进行单轴传动过程中存在速度、加速度、保证凸轮磨削工件表面粗糙度合格的最大线速度都存在最大值约束，那么凸轮磨削转速也应该满足以上约束。

采取了文献[9]中“同步滞后”的轮廓误差模型：

式中：Cc=1，eθ—理论磨削点与实际磨削点之间的角度差；Cx—理论轮廓曲线对应理论角度的二阶偏导数；er—理论磨削点与实际磨削点极坐标绝对值之差。

3 动态磨削速度优化

为了优化转速，根据CTC原理利用前一个周期的磨削情况动态调节本周期的凸轮工件磨削速度。若直接根据实际切削深度的变化进行速度优化时，当切削厚度较小时，微小的磨削深度变化会导致转速曲线发生大幅度摆动，为了避免这种情况的发生采取在准恒线速度速度曲线下进行微调的方式来实现动态速度优化。基于动态速度优化的凸轮磨削控制策略，如图2所示。

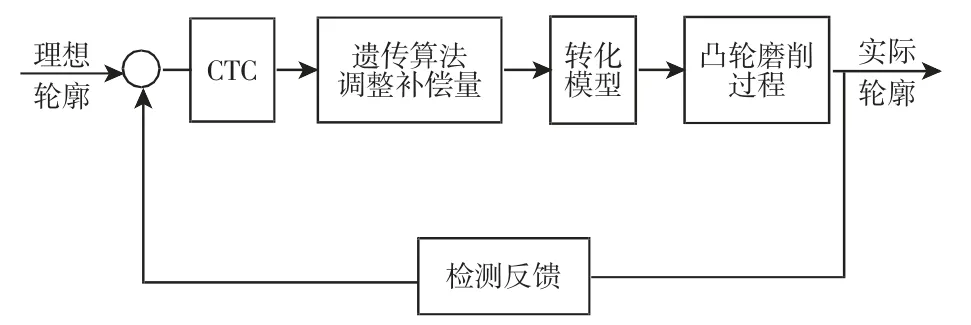
图2 基于动态速度优化的凸轮磨削控制策略Fig.2 Dynamic Speed Optimization Based Whole Control Strategy for Cam Grinding

3.1 基于CTC原理的磨削补偿量的计算

在数控磨削加工过程中，凸轮和凸轮轴属于批量生产的物品，意味着同一个加工路径将被重复进行的。

由于轴匹配度和切削点相对磨削速度和磨削进给速度不一致等因素造成，实际磨削过程中理论磨削量和实际磨削量是不相等的，但是每个加工周期都是具有相同的期望路径。为了解决这个问题提出了基于CTC的磨削补偿量计算。CTC控制是制造过程的一种控制方法，在每个加工周在每个加工周期后进行测量，通过当前周期最终输出的信息来反馈到下一个周期中，即在逐次循环的过程中利用上一个周期的磨削信息来指导本周期的磨削过程[9]。综上所述得到CTC控制的优化策略为：

式中：aepa—实际当量磨削厚度；aept—理论当量磨削厚度；aept—切点跟踪过程产生的附加当量磨削厚度；aepi—第i补偿的当量磨削厚度。

为了使实际当量磨削厚度与理论当量磨削厚度相等，令将补偿的当量磨削厚度进行水平解，得到水平方向的当量磨削厚度补偿量ΔXi+1。

3.2 补偿转换模型

若直接将产生的补偿量进行补偿，会频繁修改X轴和C轴的对应关系不利于系统稳定，并且砂轮架的惯性较大较难满足X轴的快速跟踪的性能。

由于凸轮磨削成型过程式通过进给轴X轴和旋转轴C轴联动配合下完成的，所以两轴存在着一定的对应关系，关系可表示为：XL=f（ωc），式中：XL—进给轴与凸轮圆心之间的距离；ωc—凸轮C轴转速。通过CTC原理得到修正后的X轴砂轮运动轨迹和未修正的C轴转速，通过内推可得到修正后的C轴转速和未改变的X轴进给轨迹，将X轴补偿量转换为C轴转速。

其中，XL+ΔXL=f（ωc）等价于：

在得到X轴的补偿量ΔX后可以通过转化模型将补偿量叠加到C轴转速中，但直接叠加存在很多问题，例如可能会使得C轴转速变化极大，导致磨削精度降低。

3.3 基于遗传算法的速度优化

为了得到的本磨削周期最优旋转速度，提出了基于遗传算法的速度优化方法。通过遗传算法再次调整补偿量ΔX，使得叠加于C轴后速度得到再次优化，避免出现补偿后的曲线速度与加速度波动过大。

由于在遗传算法优化过程中如果直接将所有的参数点都进行优化参数过大，并且也不利于算法收敛，所以在进行优化之前，先去除一部分对优化结果影响不大的点，例如凸轮升程曲线的基圆部分则不做优化。主要对凸轮曲率变化大的部分选取合理的参数点进行分段修正，并通过CTC原理获得凸轮补偿曲线并分段后，对分段曲线建立优化目标函数，考虑到补偿量可能会影响到凸轮磨削的线速度，C轴角加速度，所以分别考虑以上内容，建立优化目标函数为：

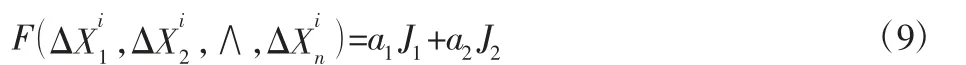
式中：ΔXi

n—第i次循环时第n点时调整后的补偿量；择为20，交叉运算方式使用单点交叉运算，变异运算使用均匀变异算，变异率为0.01。在适应度上选择基于排序的适应度分配计算方法。

J1—凸轮最大线速度与最小线速度之间的差值；

J2—C轴最大角加速速度；

a1，a2—相关权重系数。

同时该式中的补偿后的速度优化算法同样也应该满足凸轮磨床的原始约束条件。

所以这里的优化问题为：

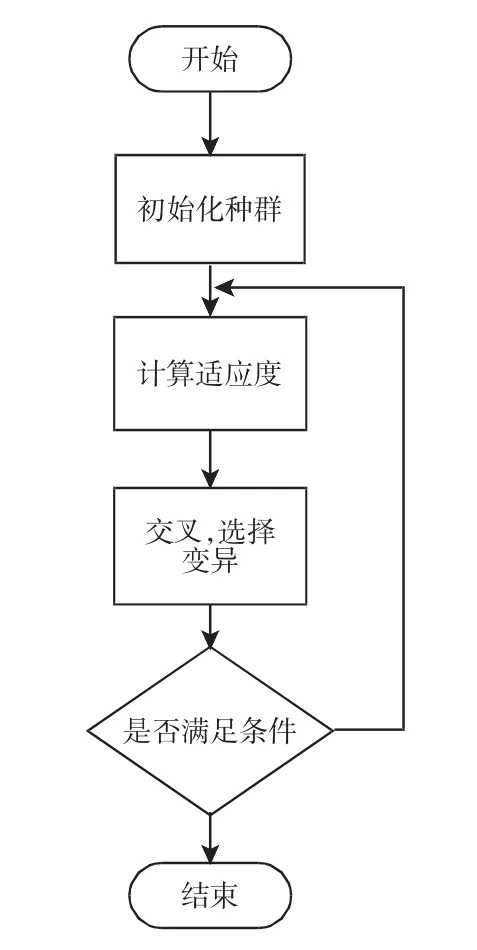
图3 遗传算法优化流程图Fig.3 Optimization Flow Chart of Genetic Algorithm

4 实验与仿真

为了验证算法的可靠性，基于文献[10]搭建Simulink仿真模模型。凸轮磨床仿真系统，如图4所示。

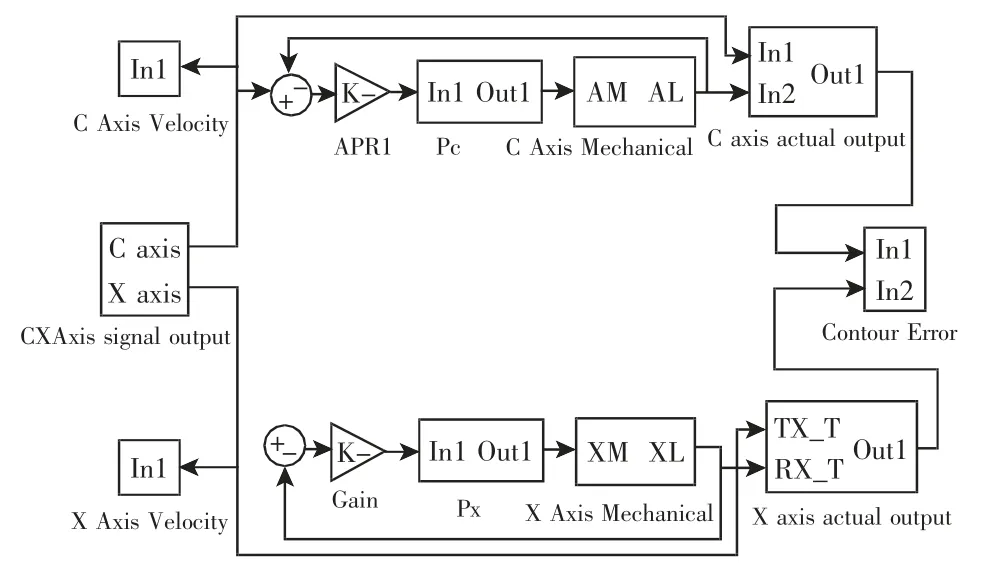
图4 凸轮磨床轴仿真模型Fig.4 Simulation Model of Cam Grinder

本次磨削中采用012W进气凸轮，凸轮基圆半径为16.8mm，砂轮直径为36mm，砂轮转速恒定为100mm/s，从动轮半径为，本次磨削厚度为1mm。优化算法如下所示：

（1）已知凸轮磨削中的相关数据利用速度顺心法，求得C轴与X轴的对应关系。

（2）利用限制最大加速度的准恒线速度方法求得C轴转速曲线。

（3）根据CTC补偿原理，通过测量凸轮磨削过程中的磨削速度与磨削后的厚度来求取补偿量，接着将磨削补偿曲线曲线进行分段。

（4）对的补偿曲线进行分段，区间中采样为3度一个点，采用遗传优化算法进行优化，优化目标函数为：

考虑到这里是基于准恒线速度模型基础上优化的速度曲线，各个磨削点之间的线速度影响较小，所以有关线速度的系数权重选择的相对较小，加速度影响权重系数选择的相对较大。优化曲线权重系数，如表1所示。

表1 优化曲线权重系数Tab.1 Optimum Curve Weight Coefficient

遗传算法分为三段优化求取补偿曲线段曲线。

（5）根据C_X转换模型，求得转化后的速度曲线。如果磨削过程中还得达不到精度要求，重复步骤3至步骤5，求取新的速度曲线。为了进一步验证算法的可靠性与实用性，分别比较几种优化方法的精度。三种磨削方法C轴速度，如5图所示。三种磨削方法的轮廓误差，如图6所示。

图5 三种磨削方法C轴速度曲线Fig.5 C Axis Speed Curve of Each Grinding Method

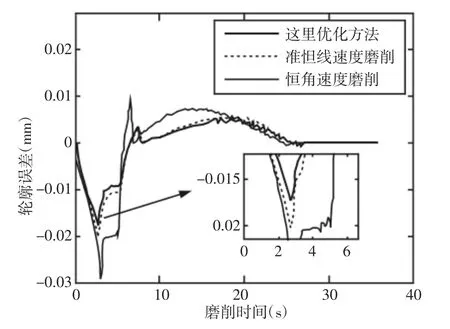
图6 三种磨削方法凸轮轮廓误差Fig.6 Cam Contour Error of Each Grinding Method

凸轮要求轮廓误差在（±20）μm内，恒速磨削在与正向负向误差较大，且磨削过程中线速度变化较快，不利于磨削质量的保证；采用近似恒线速度磨削后，负向轮廓误差与正向轮廓误差得到了减少，负向轮廓误差最大值较大；采用优化方法，正负向轮廓误差得到进一步的减小。

5 结论

提出的凸轮磨削的动态速度优化方法，是在数控磨削中的准恒线速度磨削的基础上进行的优化，并通过Matlab仿真验证了算法的有效性。相比于常用的恒角速度磨削与准恒线速度磨削，该方法磨削精度较高。