重型车床床身性能分析及多目标参数优化

杨志贤，洪后紧，顾寄南

（江苏大学制造业信息化研究中心，江苏 镇江 212013）

1 引言

机床作为工业生产的基本设备，是一个国家工业水平的标志。重型车床是现代机床的一个重要方向，各方面性能都缺乏理论依据。床身-车床核心结构，承载着加工过程中各种载荷，其动静态特性直接影响着车床加工质量。

对于床身这一复杂部件，优化方法众多，目前仍有一些不足之处。譬如，为满足较高的强度要求，通常采用较厚的尺寸获得较高的安全系数，但严重增加了制造成本，仅依靠单目标优化显然无法保证机床综合性能。在多目标优化层面，一方面，由于目标函数与约束函数的导数绝大多数都不连续，利用梯度优化求解效率低下，甚至难以找到最优解；近年来，随着人工智能的发展，更多先进的算法被用于优化领域。其中最常见的有人工神经网络、遗传算法等[1]。文献[2-3]利用遗传算法对结构进行了多目标优化，众多的研究结果表明，遗传算法对于多目标优化问题具有一定的优越性。另一方面，多目标优化结果是一组解集，各目标之间相互冲突、没有统一的度量标准，不能简单的通过加权把多个目标转化为单目标进行求解，以上文献均存在这一问题。而基于模糊综合评价法又依赖于专家的评判信息[4]，带有较大的主观性。

为解决上述问题，基于某型号重型车床床身的性能需求，采用利用客观数据的信息熵赋权的灰靶决策与遗传算法相结合的方法对床身进行多目标优化。首先借助有限元法实现床身动静态性能分析；然后以床身筋板尺寸为变量，采用正交实验法构造响应曲面，建立床身动静态性能与尺寸变量之间的隐形关系表达式；最后运用NSGA-Ⅱ进行多目标求解，在此基础之上，采用信息熵赋权的多目标灰靶决策算法选出最优方案。通过前后对比分析验证了该方法的有效性。

2 床身性能分析

2.1 机床结构介绍

某万能通用类重型卧式车床，如图1所示。该机床可加工的最大工件重量为32t，最大回转直径为1600mm，主轴转速范围为（0.86～1500）r/min。主轴箱固定于基座之上，床身与该基座不是一体的。床身采用三导轨式结构，且由两段子床身拼接而成，子床身内部包含着纵横交错的筋板，起着支撑床身导轨、保持床身刚度的作用。利用SolidWorks软件进行参数化建模，通过与ANSYS的无缝连接实现数据交换。在模型基础之上，对床身添加材料属性，床身铸造材料为HT200，其密度为7200kg/m3，泊松比为0.31，弹性模量为1.48E+11Pa，床身重23350kg。

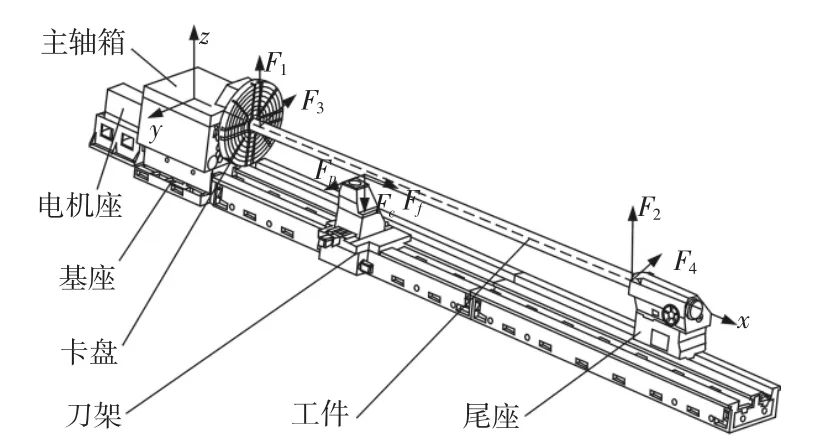
图1 某型号重型卧式车床Fig.1 A Certain Type of Heavy Horizontal Lathe

2.2 床身静力学分析

床身受力除了尾座、刀架、工件的重力以外，还包括加工过程中所受的切削力。将该力分解成沿不同坐标轴上的三个分力，如图1所示。其中进给力Ff使床身产生拉伸变形，影响很小，不予考虑。在（xz）平面内，主切削力Fc经刀架作用于床身，通过工件对卡盘和尾座将产生反作用力F1、F2，同理，F3、F4是背向力Fp的反作用力。通过分析得到：（1）床身在正常工作环境中所受最大应力为3.6606MPa，远小于材料的许用值，可忽略。（2）床身主要以水平面的弯曲为主，最大变形值为0.017641mm，发生在导轨与刀架接触面。

图2 静力学分析结果Fig.2 Results of Statics Analysis

2.3 床身动力学分析

床身振动是影响加工质量的重要因素之一，当受到外部激励F，将产生位移，如式（1）所示。

式中：X—位移（m）；K—床身刚度（N/m）；ω—激振频率（Hz）；ωn—固有频率（Hz）；ξ—阻尼比。

可见，在其他条件不变的前提下，提高系统固有频率或者增加结构刚度均能够改善床身动态性能。由于床身只有低阶固有频率才有可能同工作频率相等进而发生共振，因而只考虑低阶模态。模态分析结果，如表1所示。一阶振型图，如图3所示。

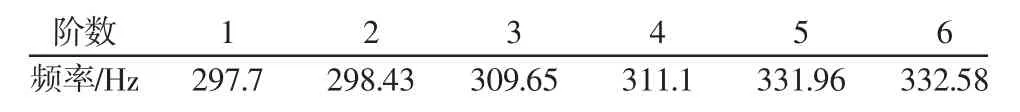
表1 床身前六阶固有频率Tab.1 The First Six Natural Frequencies of Lathe Bed

图3 一阶振型图Fig.3 First Order Mode Cloud Image

为了反映床身在动态切削载荷下的性能变化情况，通过对导轨面施加频率为（250～400）Hz的切削激振载荷，采用完全法分60步计算出床身在切削简谐力作用下的无阻尼幅频特性曲线，如图4所示。不同的激振频率对应的幅值是不同的，在横坐标为297.5Hz、310Hz、332.5Hz附近出现峰值，分别对应着模态分析的一阶、三阶、六阶固有频率。这也说明了对床身动态性能影响最大的是低阶频率。以距离外界激励频率最近的一阶固有频率大小作为指标衡量床身动态性能。

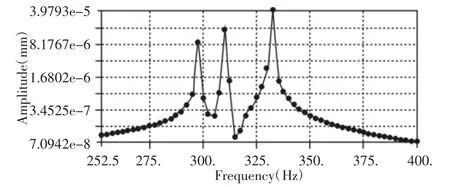
图4 幅频特性曲线Fig.4 Amplitude-Frequency Characteristic Curve

3 响应面模型的构建

3.1 设计变量确定

床身结构涉及的参数较多，若对每一个参数都进行优化，显然工作量太大。为提高优化效率只考虑对床身影响较大的参数。床身内部包括一系列由筋板均匀紧密排布的箱体结构，使床身表现出较高的刚性[5]。为此，取侧壁厚度x1，纵向筋板厚度x2，横向筋板厚度x3为设计变量。

3.2 响应面模型

响应面法以实验设计理论为指导，通过对给定样本点进行分析，利用拟合出的输入输出关系近似显性表达式分析目标与设计变量的隐性关系。其二阶响应面模型可表述为：

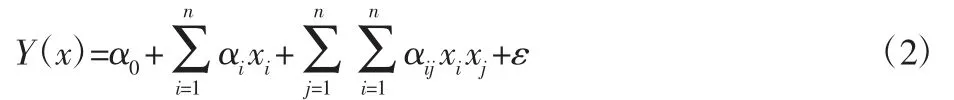
式中：α=［α0，α1，…，αn，α11，α12，…，αnn］T—待定系数矩阵，通过最小二乘法确定时，样本个数必须大于L=（n+1）（n+2）/2；n—因数个数；xi、xj—变量。

3.3 正交实验设计

样本点的选取在模型的构建中发挥着重要作用。为提高优化效率，又不影响精度，利用正交实验设计方法对床身进行分析。以床身筋板尺寸的3个参数（x1、x2、x3）作为因素，在4水平下获取的低阶固有频率、质量、静载荷下最大变形作为正交结果。结合变量许用范围，以其变动的20%作为边界，其他尺寸不变，构造因素水平，如表2所示。

表2 因素水平Tab.2 Factor Level

正交实验的样本点必然均衡分布于全面试验中，具有很强的代表性[6]，尤其适用于非线性模型。根据这一特点，构造出L16（43）正交表，如表3所示：即用16次具有代表性的部分实验代替64次全面实验分析床身筋板厚度与其动静态性能关系。

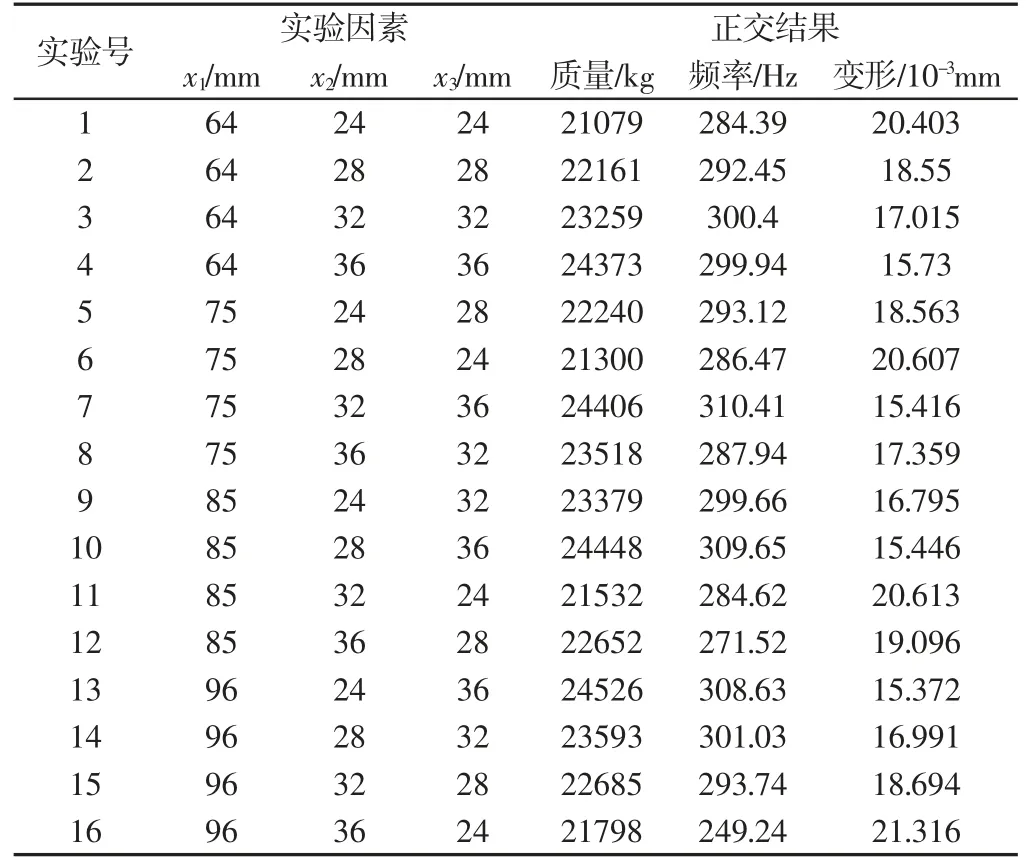
表3 L16（43）正交结果Tab.3 Orthogonal Results of L16（43）

3.4 响应面模型准确性验证

为检验模型精度，利用变相关系数评价的方法计算响应面拟合程度R2，R2越接近1表明精度越高。

式中：yi—实际响应值；y—实际响应值的均值；Yi—近似值；n—变量个数；R2—变相关系数；SSE—残差平方和；SST—总偏差平方和。

响应面与有限元分析对比情况，如图5所示。两者误差非常小。基于MATLAB编程，对应的质量、频率、最大变形系数R2分别为0.9999、0.9669、0.9984，表明拟合的响应面模型对于后续问题求解是可靠的。

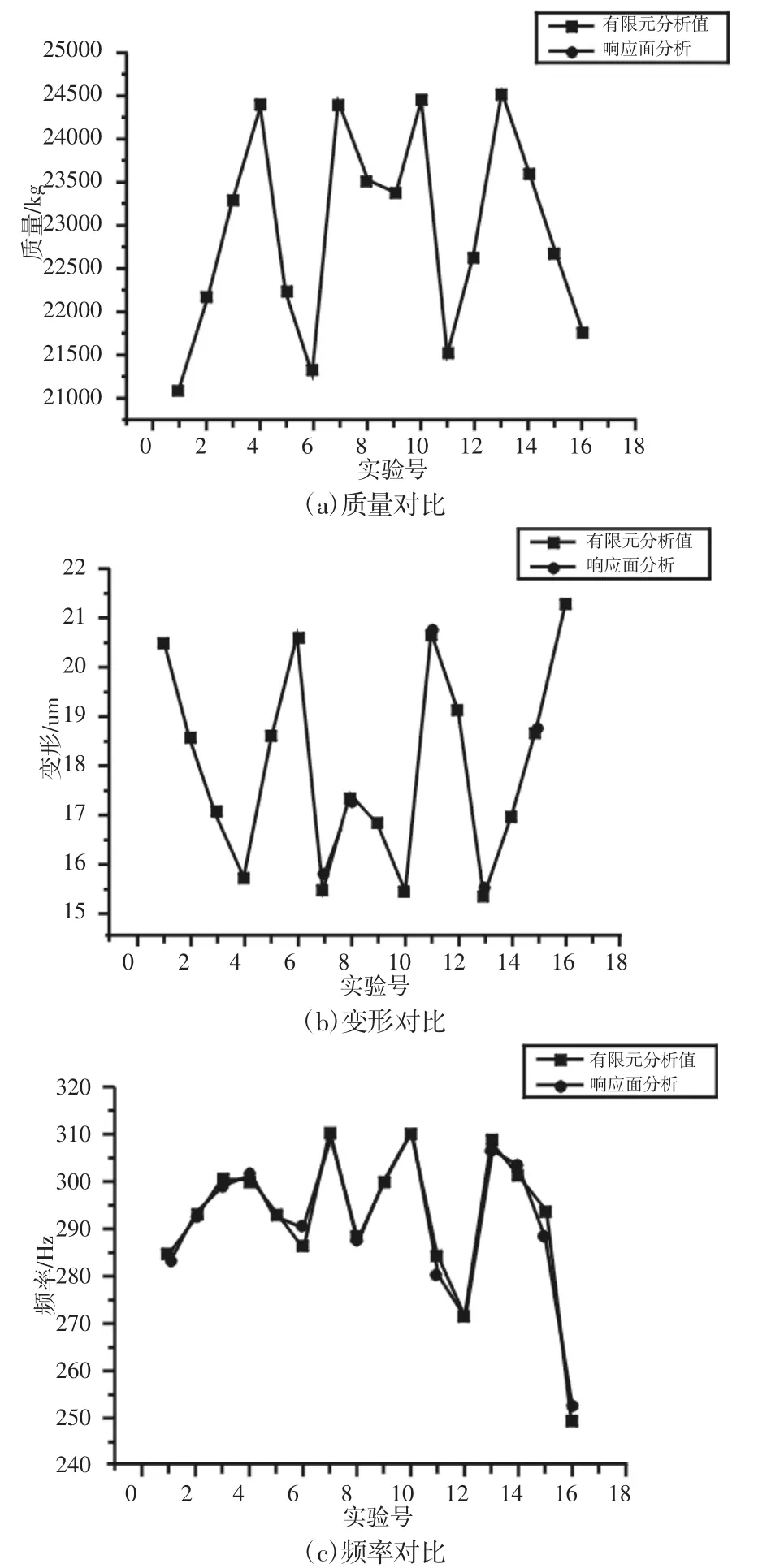
图5 有限元分析值与响应面值对比Fig.5 Comparison Between Finite Element Analysis Value and Response Surface Value

4多目标参数优化方法

4.1 优化数学模型

由于床身静态性能直接影响加工精度，因此至少要保证静态性能。建立的床身多目标数学模型为：

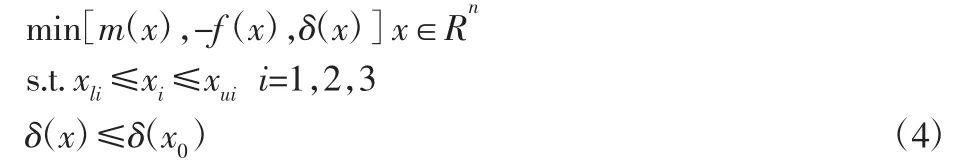
式中：δ（x）—最大变形；f（x）—一阶固有频率；m（x）—质量；xi—变量尺寸；xli、xui—变量上下限；δ（x0）—优化前床身变形值。

4.2 优化方法

遗传算法对求解多目标问题具有优越性，文献[7-8]对遗传算法进行改进，提出一种带精英策略的非支配排序遗传算法（NSGA-Ⅱ）。该算法使用了排挤算法和精英策略来代替传统遗传算法使用的共享函数算法，通过维护精英个体保持物种的多样性。MATLAB自带的gamultiobj函数是基于NSGA-Ⅱ改进的一种算法。利用该算法对床身各目标进行求解。

从Pareto解集中选择最优解是一个决策问题[9]，为避免设计人员的主观选择。采用基于信息熵赋权的多目标灰靶决策算法进行决策，过程如下：

（1）构造效果样本矩阵S=（xij）m×n，各元素均来自pareto最优解集，m表示待评估方案个数，n表示评估对象个数。

（2）通过“奖优罚劣”算子对样本矩阵S进行变换，得到决策矩阵R=（rij）m×n；

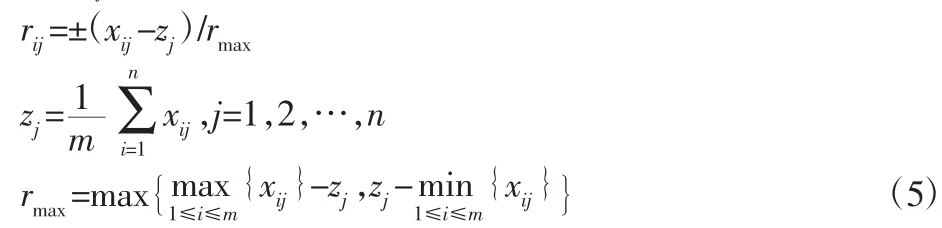
若决策目标为效益型指标，分子取正；若为成本型指标，则取负。

（3）确定最优效果向量

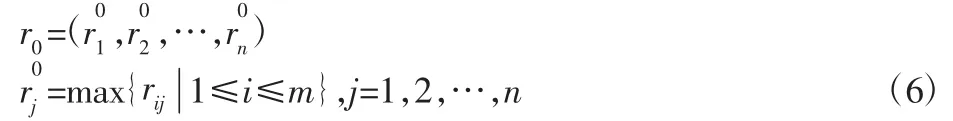
（4）计算靶心距ξi，并排序，ξi越小，则该方案越优，反之则反。

式中：uj（j=1，2，…，n）—各目标权重系数，采用熵权法确定其大小包括以下三步：

样本矩阵标准化：

计算各目标函数熵值：

4.3 优化过程及结果

通过对基于NSGA-Ⅱ的多目标优化函数gamultiobj编程，设定参数如下：种群大小为50，最大进化代数为300，最优个体系数为0.35，适应度函数偏差为1e-4。为充分保证算法的全局搜索能力，初始群体应具代表性，选择一致随机的方式得到初始群体。求得Pareto最优解集，如图6所示。从图中能够看出，这些解集符合多目标优化定义：目标之间的关系相互制约，没有一个解在三个目标上完全占优。图中每一个解均代表一种方案，Pareto解集为设计人员提供了众多选择空间。根据目标要求对各方案进行权衡之后，从中选出5组相对较优方案，如表4所示。为得到适应工程需要的最佳方案，按算法式（5）～式（10）对5组方案进行决策。计算出各方案与最优效果向量之间的距离分别为1.224、1.392、0.8223、0.8842、1.0946。即方案3最佳，对应的变量x=［76.16857，28.57627，29.64757］，考虑到实际工程中的加工要求，对尺寸圆整，并进行有限元分析。由表5可知，圆整后的一阶固有频率提高了0.15%，而最大变形降低了2.38%，其结果变化很小，可认为动静态性能基本不变，在实际工程中类似小误差是完全能够接受的。从数值上来看，床身动、静态性能略有提高。床身质量从原有的23350kg减少到22746kg，减重达604kg。

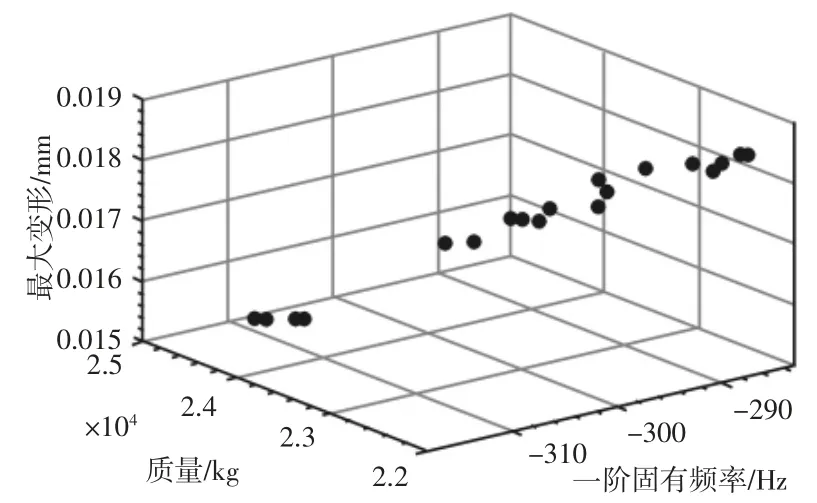
图6 Pareto最优解集Fig.6 Pareto Optimal Solution Set

表4 多目标优化解集Tab.4 Multi-Objective Optim ization Solution Set

表5 优化结果前后对比Tab.5 A Com parison of the Fore-Optim ization and Post-Optim ization Results

5 结论

以重型车床床身优化为应用实例，提出将正交实验、响应面法、遗传算法以及灰靶决策相结合的多目标优化方法，在不改变床身结构的前提下实现了尺寸动态优化。（1）基于正交实验快速建立了床身质量、变形、频率关于筋板尺寸的响应面模型，通过有限元分析值与响应面近似值对比结果表明，两者计算值误差很小，采用变相关系数评价的方法进一步验证了响应面对于后续问题求解的可靠性。（2）基于信息熵赋权的多目标灰靶决策算法能够避免主观信息对结果的影响，使得优化结果更加客观。既实现了床身轻量化，又保证了床身性能。