多场载荷作用下舵面蒙皮响应分析及寿命预估

栾孝驰，胡增辉，沙云东

（沈阳航空航天大学辽宁省航空推进系统先进测试技术重点实验室，辽宁 沈阳 110136）

1 引言

导弹舵面在真实工作环境中，气动载荷和高分贝噪声双重影响下使舵面蒙皮承受巨大的气动压力、热应力和随机声激振力。这种复杂载荷不仅改变结构刚度，也改变了材料参数和形状，使结构表现出复杂的大扰度非线性响应，严重影响打击精度，甚至导致蒙皮开裂失效，对导弹结构完整性和整体可靠性产生严重威胁[1-2]。然而模拟这种复杂的工作环境费用十分昂贵，并且获得可靠数据比较困难。因此复杂载荷下舵面蒙皮响应分析及寿命预估在导弹设计阶段起到重要辅助作用。

目前对导弹舵面研究主要集中在气动载荷响应及热模态分析。文献[3]对高超声速飞行器舵面响应分析建立了一套可行的气动热、气动力的数值研究方法。分析了舵面模态和频率随气动热和气动力的变化情况。文献[4]基于NASTRAN对一个简单翼舵模型进行了热模态分析，得出热应力影响结构刚度分布。文献[5]以导弹舵面为研究对象，针对高温环境下结构热模态激振方法进行了优化及试验验证。然而以上学者所做的工作忽略了导弹舵面在飞行中承受的高强度噪声载荷，并不能准确模拟舵面的真实工作环境。

在结构热声激振响应研究方面，文献[6]基于冯卡门大挠度理论开展了薄壁结构在热声载荷下动力学响应分析。文献[7]通过结合Monte Carlo法与Galerkin法，进一步开展了薄壁结构在热声载荷下振动响应计算与分析。文献[8]等采用有限元法研究了燃烧室热-声-结构耦合响应特性。文献[9-10]综述了热声环境下结构动态响应的研究，比较分析了热声动态响应分析方法并且总结了优缺点，先后采用了等价线性化方法、PDF/Galerkin方法对结构在热环境下的声激振响应进行求解与分析，同时该团队采用耦合的BEM/FEM法对薄壁结构在高温环境下随机声激励响应分析等方面做了大量研究[11]，并通过试验验证了该方法的有效性。

在结构疲劳寿命研究方面，文献[12]将FEM法和EL法相结合应用于热声载荷下的任意形状的层合板进行疲劳分析。文献[13]研究了不同温度对蒙皮结构的声疲劳寿命影响。分析了热屈曲对结构疲劳寿命的影响规律为先降低后增加的趋势。文献[14]建立了平均应力模型研究了各种模型下疲劳寿命，分析并总结了不同的疲劳 损 伤 模 型 优 缺 点，Goodman、Morrow、Smith-Watson-Topper（SWT）和Walker。文献[15-16]先后利用概率密度法、功率谱密度法、局部应力应变场法和改进雨流计数法等对航空航天薄壁结构在热声载荷下的疲劳寿命进行了试验研究与仿真计算。然而以上对薄壁结构所做的大量工作，没有考虑到流场对结构响应和寿命的影响。

鉴于导弹舵面真实飞行环境，在前人所做大量工作基础上，将气动载荷和噪声载荷同时考虑，加以研究不同环境下舵面蒙皮响应特性，并进行寿命预估，对导弹舵面设计阶段提供重要借鉴作用。

2 理论分析

2.1 流体动力学控制方程

导弹舵面在飞行环境中，近壁面会出现可压缩粘性流场。舵面将承受巨大的气动压力和气动热载荷。流体动力学控制方程可由可压缩Reynolds时均Navier-Stokes方程（1）、连续方程（2）、能量方程（3）和热传导方程（4）组成。

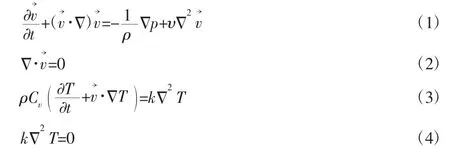
2.2 结构控制方程

导弹舵面在飞行环境中，承受高速气动力载荷，内部热应力载荷和随机噪声载荷，在多种复杂载荷作用下薄壁结构表现为大扰度随机振动。

结构控制方程可以表达为：

式中：［M］、［C］、［K］、［Fp］、［Ft］—质量矩阵，阻尼矩阵、刚度矩阵、气动压力和结构内部热应力；｛δ｝、｛σ｝—单元节点位移和应力；［D］、［B］、［H］、［N］—弹性矩阵、几何矩阵、微分算子矩阵和单元形函数。

2.3 改进的耦合BEM/FEM结构动力学控制方程

声场在结构表面形成的声压和平板结构位移之间的关系为：

式中：Hpact—声传递函数；

ua—边界声场质点的位移。

边界元法中声场控制方程如下[14]：

将式（10）和式（11）相结合，可得到声传递函数的表达式：

式中：［H］、［G］—影响矩阵；

ω—输入频率。

结构有限元控制方程为：

载荷向量｛FP｝、｛FS｝和｛FT｝分别为气动载荷、声压载荷和热应力载荷。｛d｝为位移向量，［Hs］为响应函数。

施加声载荷谱密度SIN（ω），得到结构响应谱密度（Sd（ω））n如下：

将方程（12）与方程（14）相结合，可得到输入压力功率谱密度与应力响应功率谱密度的关系为：

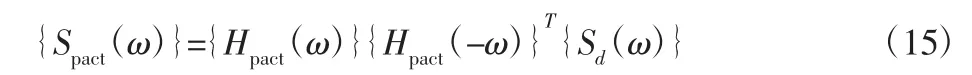
联立方程（12）、方程（14）和方程（15），可得到改进的耦合BEM/FEM平板结构动力学控制方程为：

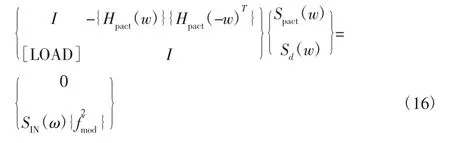
为了便于表达将方程（16）可以写为：

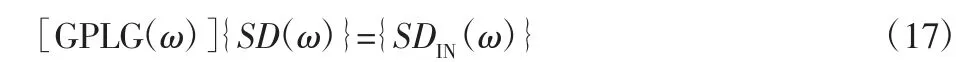
式中：｛SD（ω）｝—结构动力学响应谱密度函数；

｛SDIN（ω）｝—外界激励谱密度函数；

［GPLG（ω）］—改进的整体耦合矩阵。

2.4 疲劳寿命预估模型

平均应力模型下（Morrow）疲劳寿命：

式中：Sa—应力幅值；

Sm—应力均值。

Miner线性累积损伤表达式为：

式中：Ni—在应力水平为Si下的循环数；

Nf—该应力水平下发生疲劳失效时的循环数。

随机振动响应的损伤期望通过雨流循环矩阵和雨流损伤矩阵表示为[15]：

当E［D］=1时，结构发生破坏，以二维雨流损伤矩阵RFD（Sa，Sm）表示的结构寿命为：

3 气动载荷数值模拟与分析

主要利用自定义函数（udf）建立的热流固耦有限元计算模型，数值模真实飞行环境下C/SiC复合材料舵面蒙皮附近温度场和压力场分布，计算出蒙皮所承受的气动力载荷和气动热载荷，并分析飞行速度改变对舵面模态频率的影响。

3.1 舵面计算模型

弹道舵面及蒙皮模型，如图1所示。C/SiC复合材料属性参数，如表1所示。

图1 导弹舵面及蒙皮模型Fig.1 The Missile Rudder&Skin

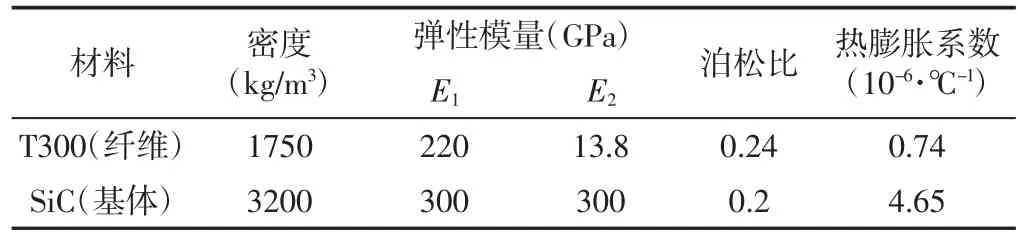
表1 C/SiC材料属性参数Tab.1 Material Property Parameters of C/SiC

复合材料蒙皮共铺设共铺设8层，每层厚度为0.25mm。铺层角度分别为0°C、-45°C、45°C、0°C、0°C、45°C、-45°C、0°C。铺层坐标系，如图2所示。

图2 导弹舵面外形与铺层坐标系Fig.2 Configuration and Ply Coordinate of Missile Rudder

3.2 流体域模型

当飞行马赫数Ma=1时蒙皮附近流体域气体温度云图、压力云图和速度矢量图，如图3所示。

图3 温度云图、压力云图及速度矢量图Fig.3 The Temperature Nephogram and Presssure Nephogram&Velocity Vectorgraph

从图3中可以看出在流体域边界层与舵面蒙皮前端交界处，速度急剧下降，压强和温度急剧升高。其主要原因是高速飞行环境下舵面前端空气强烈压缩产生停滞效应，速度降低，空气密度变大，压强变大。同时空气与舵面摩擦将气动能转化成热能，一部分直接加热在蒙皮表面，蒙皮表面再通过热传导将热能传递至整个舵面结构，蒙皮与近壁面气体又存在温度差，导致气体与蒙皮发生强制对流换热，最终达到热平衡。

3.3 蒙皮表面最高温度载荷和最大压力载荷

当飞行马赫数Ma=1增加到Ma=3.2时，舵面蒙皮表面所受的最高温度载荷和最大压力载荷，如图4所示。

图4 舵面蒙皮表面最高温度和最大压力Fig.4 The Maximum Temperature&Pressure on the Surface of C/SiC Rudder Skin

从图4左图中可以看出，飞行马赫数Ma=1增加到Ma=3.2时，蒙皮表面最高温度分别增加73.1°C、108.1°C、84.2°C、96.7°C、107.4°C、121.9°C。可知随着导弹飞行速度加快，蒙皮表面最高温度成指数式增长。超音速飞行环境下气体在蒙皮前端附近强烈压缩停滞，将空气动能转化为热能直接将舵面加热，飞行速度越快空气动能转化成热能效果越明显。从图4右图中，飞行马赫数Ma=1增加到Ma=3.2时，蒙皮表面最大压力分别为27879Pa、41196Pa、61045Pa、83721Pa、96515Pa、108992Pa、123809Pa，增 长率为47.8%、48.2%、37.3%、15.3%、12.9%、13.6%。可知随着导弹飞行速度加快，蒙皮前端最大压力成对数式增长。这是因为飞行速度增加时，蒙皮外表面边界层由于气体强烈压缩停滞形成复杂流场，密度急剧增大，速度停滞效应越显著，压力也增大。而同时温度也急剧升高，气体分子间运动加剧，改变了气体动力粘度和运动粘度，气体膨胀密度反而减小，压力也随之减小，最终压力增长趋于缓和。

3.4 不同飞行速度下前8阶固有频率

不同飞行速度环境下，导弹舵面前8阶固有频率数值解，如表2所示。因为对整个舵面进行模态分析，舵面模态频率也就是复合材料蒙皮模态频率。观察表2，模态频率随着导弹飞行速度改变而变化。在气动力和气动热双重影响下，舵面各构件变形不全相同，使舵面结构内部存在热应力，引起舵面材料的刚度、密度以及结构外形等物理因素相应改变，导致模态频率也随之改变。同时模态频率向高频偏移较小，表明飞行速度的改变对导弹舵面模态影响不大，舵面发生屈曲现象不明显。

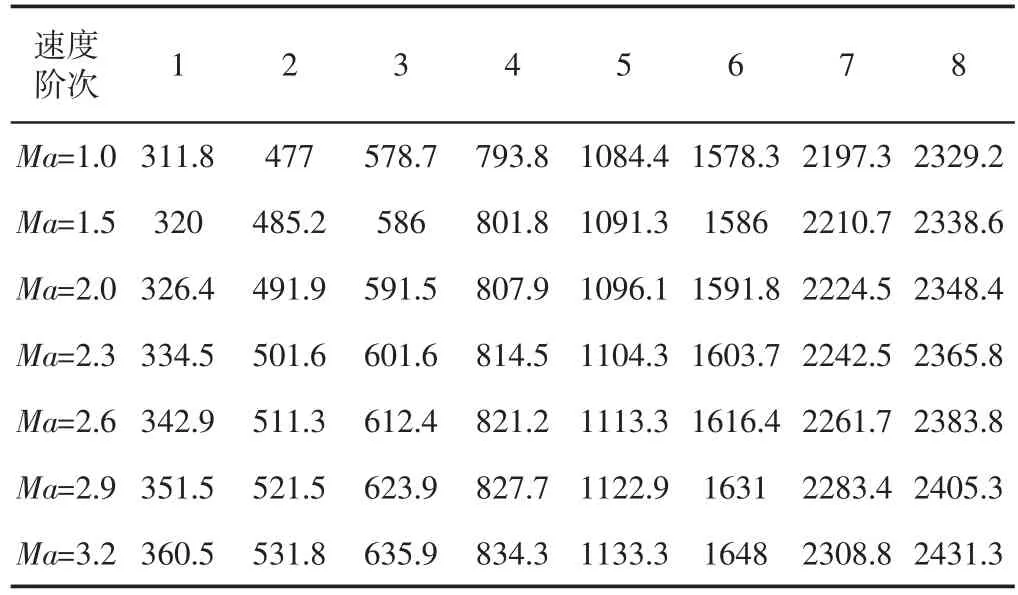
表2 不同速度下前8阶模态频率数值解/（Hz）Tab.2 The First Eight Order Modal Frequencies of the Numerical Solution in Different Flying/（Hz）

4 气动载荷与噪声载荷耦合数值模拟与分析

舵面蒙皮在真实飞行环境下不仅仅承受气动载荷，同时承受来自推进系统喷气噪声、内部运转振荡噪声和结构表面因湍流层产生的气动噪声。通过改进的耦合FEM/BEM模型将气动载荷和噪声载荷相互联系，数值模拟舵面蒙皮真实工作环境下承受的复杂载荷。由于多种噪声相互混合相互干扰，故统一采用有限带宽高斯白噪声作为声激励。声载荷频率范围（16～1600）Hz，频率间隔为4Hz，加载方式为扩散场加载。采用功率谱密度法作为输入声载荷功率谱密度，功率谱密度表达式为：

式中：Δf—频带宽度；

SPL—输入声压级。

计算带宽声压级为（140～164）dB，间隔6dB的有限带宽高斯白噪声载荷功率谱密度，数据如表3所示。

表3 有限带宽高斯白噪声载荷功率谱密度/（Pa2Hz-1）Tab.3 The Lim ited Band w idth Gaussian White Noise Power Spectral Density/（Pa2Hz-1）

4.1 舵面蒙皮响应危险点位置

由于舵面蒙皮采用C/SiC复合材料层合板，不同于普通金属结构损伤时内部变化情况，故采用Von-Mises等效应力研究疲劳。飞行马赫数Ma=1时，声压级为140dB环境下舵面C/SiC复合材料蒙皮Von-Mises应力最大点位置和位移响应最大点位置，如图5所示。可知在蒙皮外侧Von-Mises应力响应最大，在外侧底部位移响应最大。在舵面抗疲劳设计中，应该特别注意这些危险点位置。

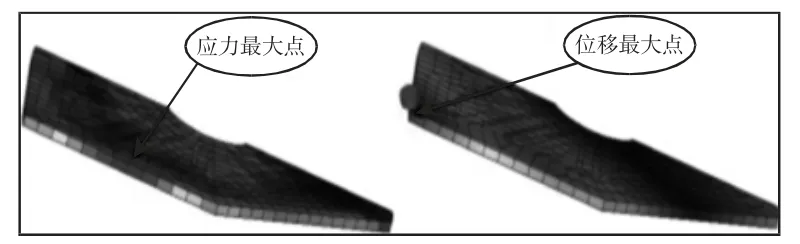
图5 C/SiC蒙皮应力和位移最大点Fig.5 The Greatest Stress Response Point and Displacement Response Point of C/SiC Rudder Skin

4.2 飞行速度对蒙皮响应的影响

舵面蒙皮危险点响应（应力最大点位置Von-Mises应力功率谱密度（PSD）和位移最大点位置位移有效值（RMS）），如图6所示。当飞行马赫数Ma=1增大到Ma=3.2时，舵面蒙皮危险点位置应力PSD（MPa2/Hz）最大值分别为7.34、8.27、8.62、9.2、9.68、11.82、13.2，位移RMS（mm）最大值分别为0.184、0.2、0.216、0.232、0.236、0.28、0.308。可见随着飞行速度增加Von-Mises应力PSD和位移RMS均升高。飞行速度增加，舵面表面温度升高，声激振响应更加强烈。不同飞行速度下结构声激振响应随频率改变呈现出大致相同的规律，因为模态频率对声激振响应起主导作用，改变飞行速度，舵面发生屈曲不明显，模态频率没发生较大变化。

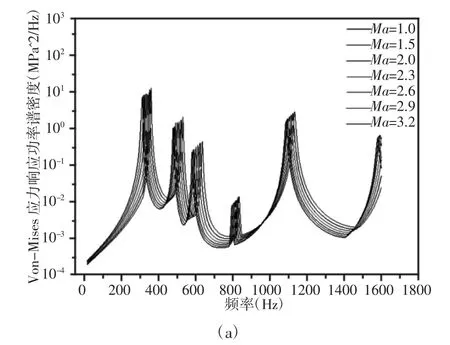
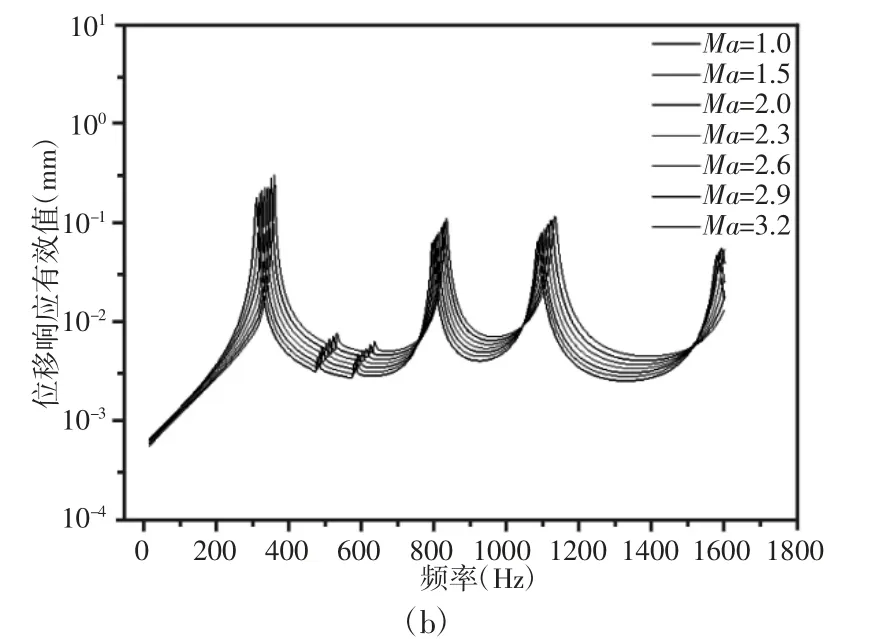
图6 不同飞行速度下C/SiC蒙皮应力响应PSD和位移响应RMSFig.6 Stress Response PSD＆Displacement Response RMS for Rudder Skin Variations of Flying Velocity

4.3 声压级对蒙皮响应的影响

导弹飞行马赫数Ma=3.2时不同声压级下C/SiC蒙皮危险点Von-Mises应力响应功率谱密度（PSD）和位移响应有效值（RMS），如图7所示。C/SiC蒙皮Von-Mises应力PSD（MPa2/Hz）最大值分别为13.2、52.5、209.1、832.2、3313，位移RMS（mm）最大值分别为0.308、0.614、1.226、2.446、4.88。在一阶固有频率附近Von-Mises应力PSD和位移RMS达到最大值，声压级每增大6dB，应力响应功率谱密度增加约三倍，位移有效值增加约一倍。不同声压级下薄壁板危险点位置Von-Mises应力PSD和位移RMS分析表明，在（16～1600）Hz频带高斯白噪声载荷作用下，固有频率附近都被激起了响应峰值，说明基频在声激振响应中具有主导作用，一阶固有频率附近峰值最大，高阶频带范围内的峰值相对较小，表明在抗声疲劳结构设计中应当考虑响应谱的频率特征。

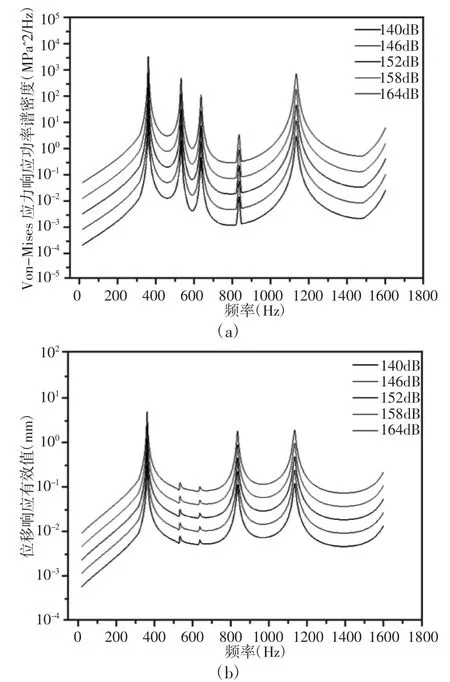
图7 不同声压级下C/SiC蒙皮应力响应PSD和位移响应RMSFig.7 Stress Response PSD＆Displacement Response RMS for Rudder Skin Variations of SPL

5 复杂载荷下舵面蒙皮寿命预估

利用改进雨流计数法对蒙皮应力响应进行数据计数，通过Morrow平均应力模型将应力全部转化成零均值应力循环，再结合Basquin疲劳寿命模型对该类型C/SiC复合材料层合板零均值循环进行曲线拟合，可得出S-N曲线表达式为[17]：

然后通过Miner线性累积损伤理论对舵面蒙皮在复杂载荷下进行疲劳寿命预估。当声压级为140dB，导弹飞行马赫数分别为Ma=1、Ma=2和Ma=3.2时，舵面蒙皮危险点雨流循环矩阵（RFM）和雨流损伤矩阵（RFD），如图8所示。

图8 RFM和RFD随飞行速度变化规律Fig.8 RFM and RFD Variations of Flying Velocity

可知Von-Mises应力响应循环幅主要集中在左上角靠近中心点附近，表明应力响应幅值偏小。随飞行速度增加，有向外扩散趋势，幅值略微偏大。随导弹飞行速度改变结构损伤程度略微加强，变化不大。

当导弹飞行马赫数Ma=3.2时，声压级为140dB、152dB、164dB时，舵面蒙皮危险点雨流循环矩阵（RFM）和雨流损伤矩阵（RFD），如图9所示。从图9可知Von-Mises应力响应循环随声压级增大在副对角线附近扩散明显，且应力响应幅值急剧变大。从图9可知随声压级增大结构损伤程度由10-11增加到10-4，这是因为疲劳循环幅值增加引起结构内部损伤增加当导弹飞行马赫数Ma=1增大到Ma=3.2，声压级为（140～164）dB，间隔为6dB时，采用改进雨流计数法结合Miner累积损伤公式得出C/SiC复合材料舵面蒙皮寿命，如图10所示。可知随着飞行速度加快，蒙皮疲劳寿命在马赫数Ma=1到Ma=2.3之间下降较明显，马赫数Ma=2.3至Ma=3.2之间下降趋势逐渐变缓。因为C/SiC复合材料层合板是在高温环境下（约1000°C）备制而成，在纤维轴向方向碳纤维热膨胀系数远低于碳化硅集体热膨胀系数，结构内部存在残余拉应力，在外部载荷力作用下界面滑动损伤更大，导致结构沿着纤维轴方向容易开裂。随着导弹飞行速度加快，蒙皮表面压力上升趋势减慢，温度急剧升高，层合板内部残余拉应力逐渐消失，寿命下降趋于平缓。由于随着飞行速度加快，寿命下降不太明显，也表面舵面附近声场与压力场和温度场都为弱耦合。当增大声压级时，疲劳寿命成对数式下降。飞行马赫数Ma=3.2，声压级为140dB、146dB、152dB、158dB、164dB时，寿命分别为2382171s、187238s、24203s、3024s、336s依次降低约92%、87%、85%、89%。随着声压级加大，对舵面疲劳寿命影响特别严重，表面噪声激振在导弹舵面可靠性设计中尤为重要。

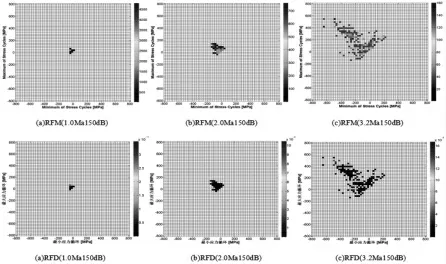
图9 RFM和RFD随声压级变化规律Fig.9 RFM and RFD Variations of SPL

图10 疲劳寿命随飞行速度和声压级变化规律Fig.10 Fatigue Life Variations of Flying Velocity and SPL

6 结论

（1）结合自定义函数（udf）建立的热流固耦合有限元控制方程和边界元声场控制方程，推出改进的耦合BEM/FEM计算模型，能够较准确地模拟舵面蒙皮在真实飞行环境下承受的复杂载荷，对导弹设计阶段起到重要辅助作用。

（2）通过数值仿真，计算出了舵面蒙皮Von-Mises应力响应和位移响应最大点位置。并且声压级每增大6dB，应力响应PSD增加约三倍，位移响应RMS增加约一倍。在舵面蒙皮抗疲劳设计中起到重要借鉴作用。

（3）从雨流循环矩阵和雨流损伤矩阵可知，改变飞行速度，应力响应循环主要集中在左上角靠近中心点附近，表明应力响应幅值偏小，结构损伤程度不大。当声压级增大，应力响应循环在副对角线附近扩散明显，且应力响应幅值急剧变大，结构损伤明显加快。

（4）随着导弹飞行速度加快，舵面蒙皮寿命下降不太明显，并且趋于缓和。随着声压级加大，疲劳寿命成指数式下降，表明在高分贝噪声环境下舵面蒙皮疲劳失效主要由声激振引起。