求解多Hoist循环调度问题的帝国主义竞争算法

毛永年，唐秋华，张利平

（1.遵义师范学院工学院，贵州 遵义 563000；2.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉 430081；3.武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉 430081）

1引言

Hoist调度问题[1]来源于以生产印刷电路板（Printed Circuit Board，PCB）为代表的电镀生产线。

印刷电路板（PCB）是计算机、手机、以及几乎所有自动化设备的重要元器件。在制造PCB的电镀工艺环节，工件（半成品）需要依次经历多个处理槽以完成必备的工艺要求。工件在这些处理槽中的加工过程具有一定的柔性，即工件的加工时间可以在给定的上下限范围内变动。工件的这种允许变动的加工时间范围被称为时间窗口。受计算机编程控制的Hoist必须在给定的时间窗口内，将工件从当前处理槽转移到其下一工序所在的处理槽；否则，工件将会因为制造缺陷而产生质量问题。为了便于管理，自动化的电镀生产线常采用循环生产模式，即Hoist在每一个生产循环内执行相同的搬运作业序列以完成大批量工件的生产。因此，规划与调度Hoist搬运作业对系统的生产效率、产品质量有重要影响。为了克服由运输设备（Hoist）造成的生产瓶颈，同一条轨道上通常安装有多台Hoist以协同完成电镀生产线上的运输作业。典型的多Hoist电镀生产线布局，如图1所示。图中，处理槽呈线性排列，且工件的入口和出口在同一个位置，在处理槽上方的轨道上，多台Hoist同时保持运行。

虽然，多台Hoist协同作业可以显著提高电镀生产线的生产效率[2-3]，但同时也增加了调度Hoist搬运作业的难度。首先，相比于基本的单Hoist调度问题[1]，多Hoist调度不仅要决策搬运作业的执行时间，同时还要决策Hoist的分配，从而使得问题规模变得更为庞大。此外，由于多台Hoist在同一条轨道上运行，必须处理它们之间潜在的碰撞冲突，从而增加了调度的复杂性。

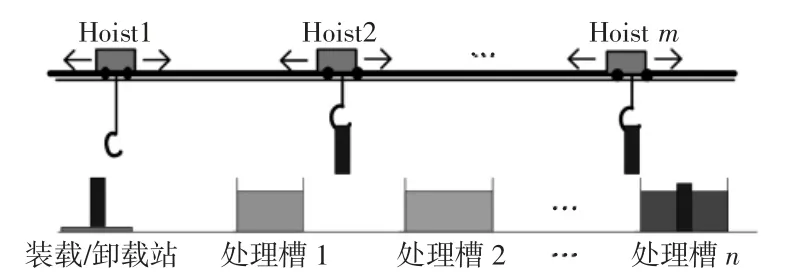
图1 多Hoist电镀生产线示例Fig.1 The Example of Electroplating Production Line with Multiple Hoists

文献[3]首次提出了多Hoist循环调度问题的混合整数线性规划（MILP）模型。针对该模型中Hoist搬运作业不能跨越周期的缺陷，文献[4]提出了一个改进的MILP模型以完善文献[3]的模型。针对具有双向工件运输流的电镀生产线，文献[2]分析了多种Hoist避碰条件，提出了该问题的MILP模型以及基于混合整数规划的分支定界算法。此外，基于启发式的求解方法[5-6]被提出以求解针对只有两台Hoist的循环调度问题。由于时间窗口约束使得该类问题的可行解空间十分有限，研制针对此类问题的元启发式算法变得极为困难。现有的相关研究[7-9]仅考虑一个运输资源（Hoist/Robot）的情形。针对多Hoist调度，文献[10]将电镀生产线划分为若干个互不重叠的区域，每台Hoist只负责一个区域内的搬运作业，并使用模拟退火算法求解最佳的区域划分方法。然而，由于区域划分的方法限制了Hoist可能的移动区域，因而该方法不具有最优性。此外，区域划分的方法不适合的具有双向工件流的电镀生产线，如图1所示。

首次提出使用基于群智能的元启发式算法（帝国主义竞争算法）求解考虑具有重叠区域的多Hoist/Robot循环调度问题。首先，基于搬运作业的最小时间间隔法建立该问题的MILP模型。考虑到此类问题的可行解空间极为有限这一特点[8]，在设计算法时，提出在给定Hoist分配条件下的启发式目标函数以引导种群向有利方向进化。同时，为了提高算法搜索效率和求解质量，针对种群进化过程中产生的大量不可行解，提出基于Hoist分配的可行解修复策略以修复搬运作业的优先关系。最后，与专业优化软件CPLEX以及遗传算法的对比测试结果验证了所提出的方法的有效性。

2 问题描述和数学模型

研究图1所示的电镀生产线，包括m台Hoist、n个处理槽。其中装载站0和卸载站（n+1）同在一个位置。Hoist的编号从左到右依次是1、2、…、m。每个工件自装载站进入系统，依次经历从处理槽1到处理槽n，最后被Hoist运输到卸载站。装载/卸载站的容量设为无限大。处理槽1至n的容量为1个工件。由于处理槽之间没有缓冲设施，工件在当前处理槽完成加工后（必须满足时间窗口约束），须立即被Hoist运输到下一个工序所在的处理槽。

文献[2]基于搬运作业的最小时间间隔法构建了具有无碰撞约束的最优化MILP模型，为了研究方便，对该模型进行了简化处理，并使用如下定义：

搬运作业i—Hoist将工件从处理槽i上取出，然后将其搬运到处理槽i+1，最后将其卸载到该处理槽内的全部过程，0≤i≤n；

Li—工件在处理槽i上的最小处理时间，0≤i≤n；

Ui—工件在处理槽i上的最大处理时间，0≤i≤n；

di—执行搬运作业i所需的时间，0≤i≤n；

αh—搬运作业i的优先级高于搬运作业j时，执行此两项搬

ij运作业的最小时间间隔。其中h=q-p，p、q分别为执行搬运作业i和j的Hoist编号。

M—足够大的正数。

该问题的决策变量为：

T—周期长度；

ti—执行搬运作业i的开始时间，0≤i≤n；

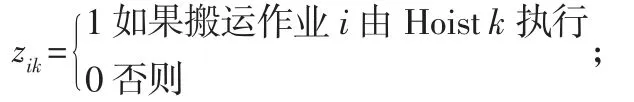
0≤i≤n，1≤k≤m；

文献[2]模型的简化版可以表示为：

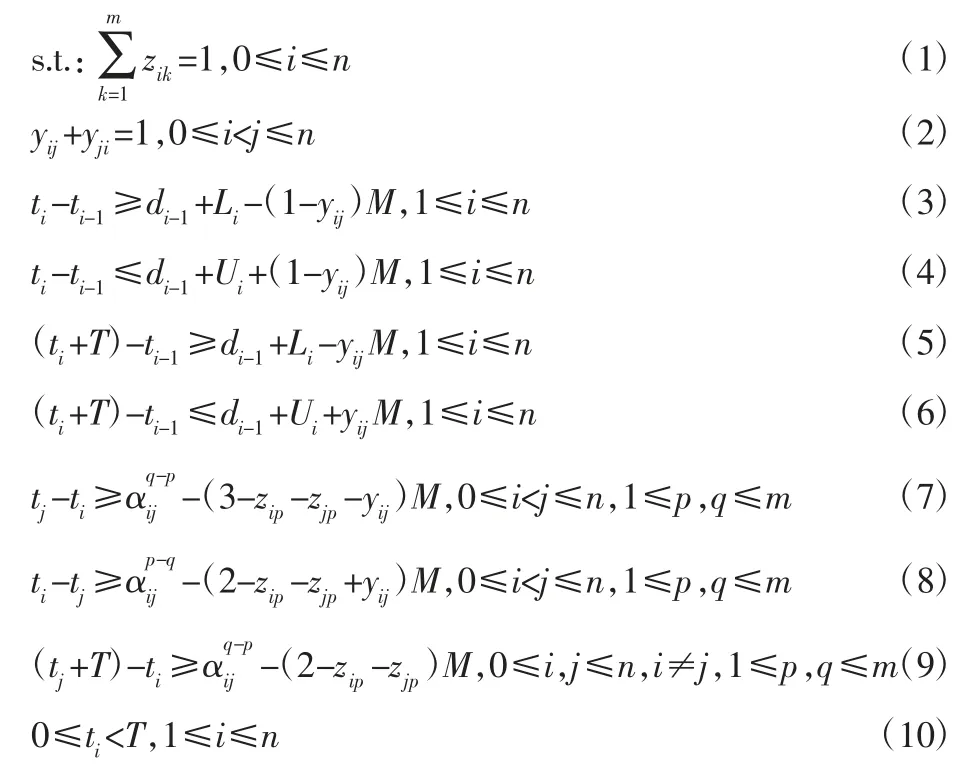
模型的目标函数是最小化周期长度T。式（1）表示任何一项搬运作业只能分配给一台Hoist。式（2）强调任意两个搬运作业之间只有唯一一种优先关系。式（3）～式（6）为时间窗口约束。当yi-1，i=1时，式（3）～式（4）强调工件的加工时长不小于允许的最小加工时间Li同时不大于允许的最大加工时间Ui。当yi-1，i=0时，工件在处理槽i上的加工跨越了两个周期，那么工件的实际加工时长为（ti+T）-（ti-1+di-1）。式（5）～式（6）表示，当yi-1，i=0时，工件的加工时长同样不小于允许的最小加工时间Li，同时不大于允许的最大加工时间Ui。式（7）～式（9）是与Hoist移动轨迹相关的约束。假设Hoist p执行搬运作业i、Hoist q执行搬运作业j（即zip=zjq=1），式（7）表示当搬运作业i的优先级高于搬运作业j时（即yij=1），搬运作业i、j的开始时间间隔tj-ti不小于参数αq-pij，从而保证执行搬运作业i、j的Hoist有足够的时间来完成相应的移动或者避免潜在的碰撞冲突。当yij=0时，式（8）与式（7）的情形相反。式（9）保证Hoist移动轨迹在两个周期之间的连续性，即：在完成上一周期内的搬运作业后，每一台Hoist都有足够的时间回到下一个周期的起始位置。不失一般性，式（10）表示任何搬运作业的开始时间必须在一个周期［0，T）的调度域内。

3 改进的帝国主义竞争算法

帝国主义竞争算法（ImperialistCompetitive Algorithm，ICA）[11]是一种受社会行为启发的群智能随机搜索算法，该算法在调度及优化等领域得到广泛应用[12]。与遗传算法[13]相比，ICA的多种群进化机制使得算法不易陷入局部最优。利用该特点，同时将遗传算法（GA）的交叉、变异操作引入到ICA的同化机制中，使得改进的帝国主义竞争算法同时具有GA的特征。

3.1 编码方式

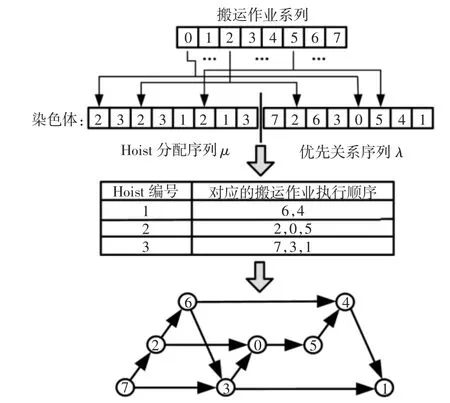
图2 编码示例Fig.2 An Example of Coding

染色体编码由两部分组成，分别用序列μ=｛h0，h1，…，hn｝与λ=｛x0，x1，…，xn｝序列表示种群中任意一条染色体。序列μ中的第i个基因hi对应执行搬运作业i的Hoist编号；序列λ中的第i个基因xi所拥有的搬运作业优先级为i。序列λ中的搬运作业越靠前，其优先级越高。用8项搬运作业为例说明了此编码方式，如图2所示。在图2中，由于基因“2”分别在序列μ中的第0、2、5个位置出现，因此，编号为0、2、5的搬运作业分配给2号Hoist执行。其次，由于此三项任务在序列λ中出现的顺序为2、0、5，因此，2号Hoist按照此顺序依次执行这三项搬运任务。同理，可获得其它Hoist的搬运作业以及排序。此外，根据搬运作业在序列λ中出现的先后顺序，也可获得由不同Hoist执行的搬运作业之间的优先关系。

3.2 启发式评价函数

所研究问题的标准目标函数为：

当搬运作业优先关系序列λ和Hoist分配序列μ为已知时。式（1）～式（10）则可转换为如下形式：

式中：a—实数，b的取值为-1、0或者1。

事实上，式（12）是一类特殊的线性规划问题，可以用赋权有向图来描述[7-8]。文献[14]提出了计算复杂度为o（n2m log n）的多项式算法以求解此问题，此处n为图中节点数量，m为图中弧的数量。为了提高算法运行效率，在使用文献[14]中的多项式算法求解染色体（u，λ）的最短周期T之前，可先对染色体（u，λ）进行可行性判断。如果该染色体不可行，则可直接设置f1=T0，其中

染色体（u，λ）的不可行主要由Hoist移动能力不能满足工件的加工时间窗口所导致。当yi-1，i=1时，若序列｛x0，…，i-1→…→i，…，xn｝中从搬运作业i-1到搬运作业i的优先关系序列不可行，则染色体（u，λ）一定不可行；当yi-1，i＝0时，若序列｛i-1→…xn|x0→…→i｝中从搬运作业i-1到搬运作业i的优先关系序列不可行，染色体（u，λ）也一定不可行。为了方便描述，定义序列Sj为序列λ中分别以搬运作业i-1开始、搬运作业i结束的一串有序优先关系子序列。由于一个循环序列λ包含n个Sj，因此，任意一个子序列不可行都会导致整条染色体不可行。交叉、变异操作会产生大量的不可行解，这些不可行解隐含了种群的进化信息，为了区分这些不可行解，记参数ω为所有不可行子序列S的个数之和，并采用式（13）计算不可行染色体的适应度值。

为了统一染色体适应度值的计算，采用公式（14）来计算任意一条染色体的适应度值。

对于序列Sj，可采用的算法来判断其可行性，如图3所示。

图3 子序列的可行性判断Fig.3 Feasibility Judgment of Subsequence

3.3 同化与竞争

同化、竞争是ICA的两个进化机制。在ICA中，帝国和其所属的殖民地可以看成一个独立的种群。种群中适应度值最好的一条染色体（解）被视为帝国，其它染色体都为其殖民地。每个帝国（种群）的进化是通过其内部的同化机制实现的。而帝国之间争夺殖民地的过程被成为竞争，该过程体现了帝国（种群）之间的信息交流。在标准的ICA中，同化是所属殖民地全部向帝国靠近的过程。引入遗传算法的进化机制实现此过程。具体的，利用锦标赛选择法进行选择操作，针对搬运作业的优先关系序列λ使用双点交叉操作，如图4所示。针对与之对应的Hoist分配序列μ使用单点交换交叉操作，如图5所示。针对序列λ的变异操作使用Swap变异，即随机选择两个基因位置并交换其基因，针对序列μ则使用随机变异。

图4 针对序列λ的双点交叉操作Fig.4 Two-Point Crossover for Sequenceλ

图5 针对序列μ的交换交叉操作Fig.5 Swap Crossover for Sequenceμ

使用标准的ICA竞争机制，即势力最大的帝国夺取势力最小的帝国中最弱的殖民地个体，因此，各帝国殖民地的规模在竞争中动态变化。考虑到所研问题可行解空间极少这一特点，设置一个参数ρ（0<ρ<1），ICA在每次迭代中以小于ρ的概率进行竞争操作，从而适当控制殖民地掠夺这一过程，以尽可能的维持种群的多样性。

3.4 给定Hosit分配时的不可行解修复策略

由于算法进化过程会产生大量的不可行解，针对不可行解的修复策略对提高算法的运行效率十分关键。在给定Hosit分配时，仅仅修复序列λ的某个特定子序列Sj往往会导致序列λ的其它子序列不可行，从而影响到修复策略的实际效果。这里提出，在修复不可行子片段Sj时，采用联动机制，即在修复Sj子片段后同时修复与其相关的上游子片段Sj-1或者下游子片段Sj+1，并根据搜索进程不断更新修复目标S，直到满足终止条件。同时，使用方向禁忌表v记录序列λ中各基因的移动方向，从而避免迂回搜索。针对序列λ的修复策略具体列出，如图6所示。

图6 不可行解修复策略Fig.6 Repair Strategy for Infeasible Solution

3.5 改进的帝国主义竞争算法步骤

综上所述，设计的帝国主义竞争算法步骤如下：

Step1：设置种群总规模Npop、帝国主义国家数量Nimp、竞争概率ρ、交叉概率Pc、变异概率Pm、最大修复循环次数η。

Step2：随机初始化种群，平均分配殖民地。

Step3：对帝国Ci（1≤i≤Nimp）进行评价，保存帝国Ci新产生的最好解。如果帝国Ci没有新的最好解产生，则应用精英保留策略，即：用帝国Ci的历史最好解随机替换Ci的一个殖民地。

Step4：更新全局最优解。如果满足终止条件则算法停止；否则，进入下一步。

Step5：对帝国Ci（1≤i≤Nimp）进行同化、竞争操作。

Step6：对种群中的不可行解进行可行性修复。跳转到Step3。

4 算法验证

为了验证算法的性能，在CPU为3.2GHz的PC机上使用C++语言对改进的ICA进行编码。同时，将遗传算法（GA）作为对照项。GA使用与ICA相同的交叉、变异操作。此外，在Microsoft Visual Studio 2010软件平台下调用专业优化软件IBM ILOG CPLEX（版本12.5）求解MILP模型以获得案例的最优解。

标杆案例P&U[1]的测试结果，如表1所示。该案例的参数设置与文献[2]相同。ICA的相关参数设置为：Npop=60，Nimp=3，ρ=0.1，Pc=0.9，Pm=0.1，η=3。针对GA，除了设置Nimp=1以外，其它参数设置与ICA相同。ICA和GA的终止条件为：全局最优解连续200代不更新则终止。

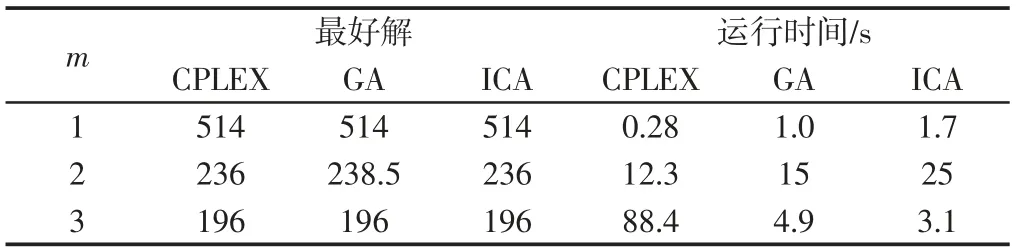
表1 标杆案例P&U的测试结果Tab.1 The Result of Benchmark Instance P&U

从表1可以看出，GA和ICA在较快的时间内给出了标杆案例在m=1和m=3时的最优解；当m=2时，ICA给出了最优解而GA给出了近优解。

为了进一步验证算法的性能，使用CPLEX、GA、ICA求解了问题规模n分别为10、12、14、16、18时的随机案例。随机案例的设计方法与文献[2]相同。ICA的相关参数设置为：Npop=100，Nimp=4，ρ=0.1，Pc=0.9，Pm=0.1，η=5。针对GA，除了设置Nimp=1以外，其它参数则与ICA相同。终止条件为：迭代次数达到200（n-5）代终止。针对每一个问题规模，30项随机案例求解结果的平均值，如图7、表2所示。

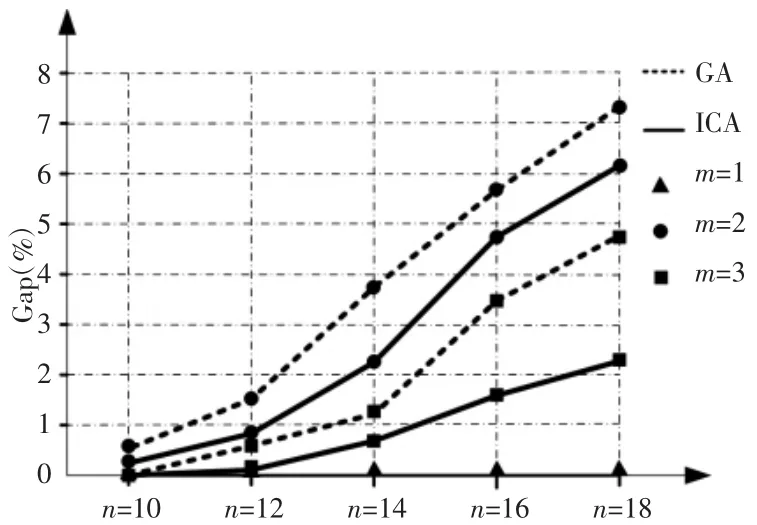
图7 GA和ICA所获得的最好解与最优解的平均百分偏差Fig.7 The Mean Gap（%）of Solusion by GA and ICA Compared with the Optimal Solution

从图7可以看出，当m=1时，GA和ICA每次都能获得最优解。这表明所提出的算法针对带时间窗口的单Hoist循环调度问题十分有效。当m=2、3时，GA和ICA所获得的结果与最优解有一定的偏差，ICA的结果要优于GA。此外，针对同样的问题规模，算法的偏差并没有因为Hoist数量的持续增加而扩大。相反，m=3时算法所获得的结果要明显比m=2时更接近最优解。

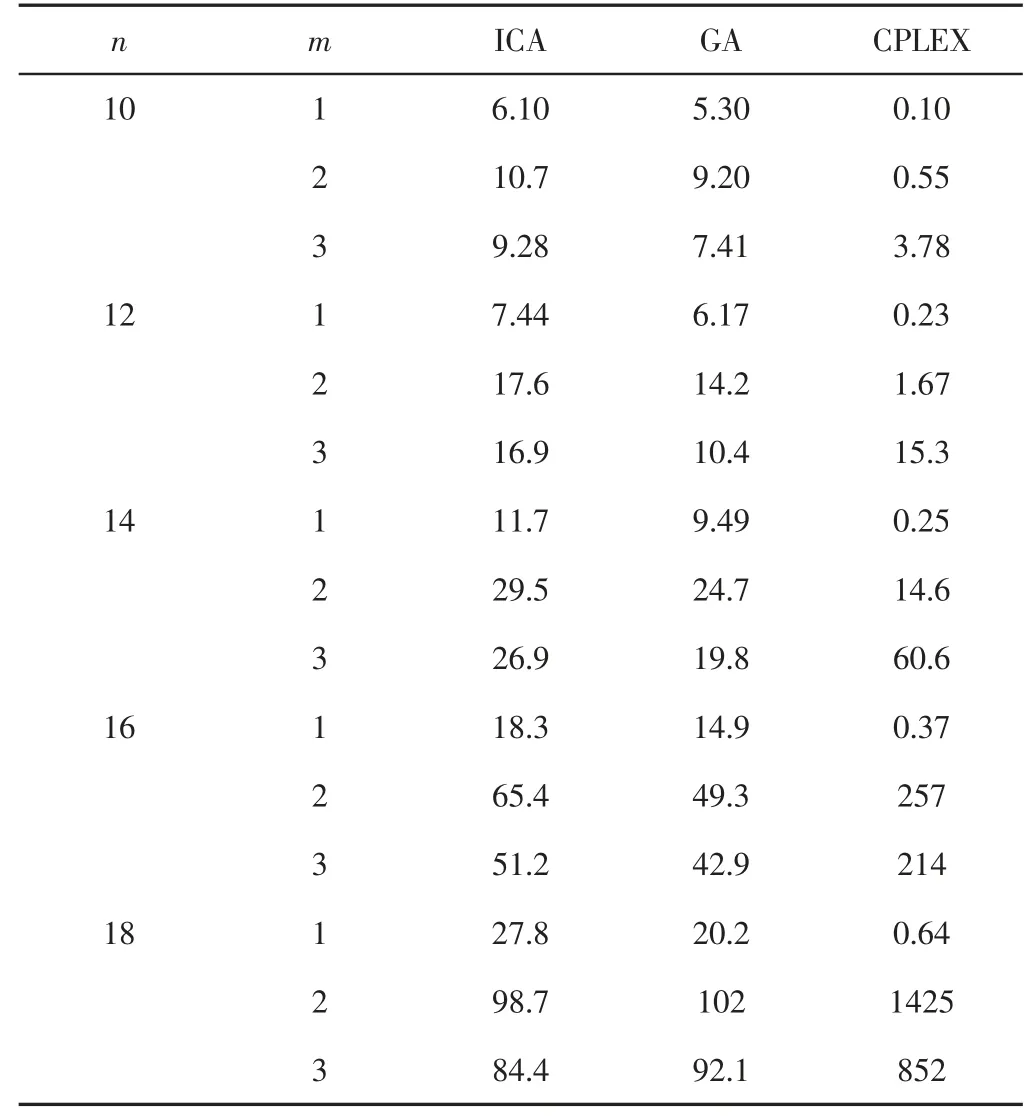
表2 随机案例的平均运行时间/sTab.2 The Mean CPU Time（s）for the Random ly Generated Instance

另一方面，从表2所给出的运行时间来看，ICA的求解时间要略大于GA的求解时间。此外，在求解小规模问题时，CPLEX表现出了较快的求解速度。但是，由于问题的解空间随着m或n的增大而快速扩大，当m与n增长到一定程度时，CPLEX的求解时间则要远远大于群智能算法（ICA/GA）所需要的运行时间。因此，ICA/GA在求解中等或者大规模问题时展现出了较强的优势。

5 结论

首次提出基于群智能的元启发式算法（ICA）求解带时间窗口的多Hoist循环调度问题。将Hoist搬运作业的优先关系以搬运作业序列的方式来表达，以方便处理Hoist无碰撞约束。提出了在给定Hoist分配条件下的启发式目标函数，同时，针对种群进化过程中产生的大量不可行解，提出了搬运作业优先关系的修复策略以提高算法的搜索效率以及求解精度。最后，基于标杆案例和随机案例，分别与专业优化软件CPLEX以及遗传算法进行对比，测试结果验证了所提出的方法的有效性。