面向核环境的侧杆式拨爪机械手分析及仿真

张明路，郭 鹏，田 颖，吕晓玲

（河北工业大学机械工程学院，天津300130）

1 引言

近年来，工业机械手在航空航天、机械制造、核环境检测等领域的应用越来越广，因而其工作的高效性、稳定性和精确性也越来越为人所关注。大量科研人员投入精力研究机械手的优化设计及运动学分析，以期获得更稳定更精确且效率更高的工业机械手。

文献[1-2]对新型机械手进行了结构设计；文献[3]对一种抓胎机械手进行了优化和分析；文献[4-5]对DH法建立连杆坐标系规则和改进方法做了研究；文献[6-9]对机械手正向运动学及奇异性做了分析及仿真；文献[10]对机械手逆向运动学做了分析。以上研究均以开环多关节机械手为主，未对此类侧杆式机械手做出结构分析。

针对特殊核电环境，圆周上均布的四个活接螺栓需要同时拨开和拨回，以实现对滤芯外盖的固定，如图1（a）所示。提出了一种侧杆式拨爪机械手，如图1（b）所示，对此类机械手进行结构分析及优化。通过分析铰接点位置确定其与末端点运动范围的关系；结合工况条件，确定拨爪尺寸选取规则；借助侧杆-拨爪-拉伸杆三者的尺寸关系研究运动学特性，得到机械手末端位姿，为分析此类侧杆式拨爪机械手运动学提供解决方法；借助仿真软件讨论机械手作业的稳定性。从而为该特殊环境下的机械手工程应用提供理论依据和仿真数据。

图1 机械手结构及工况示意图Fig.1 The Schematic Diagram of Manipulator Structure and Working Condition

2 机械手结构分析

2.1 侧杆式拨爪机械手组成及工作原理

此类侧杆式机械手由四个拨爪、四个侧杆、一个拉伸杆和一个套筒组成。所述拉伸杆前端穿过套筒与四个拨爪连接，拉伸杆后部设有齿条，电机的输出轴上固定的齿轮与拉伸杆上的齿条相啮合；所述套筒的外部通过销轴连接侧杆，每个侧杆的另一端通过销轴连接拨爪的中部。当电机转动后，通过正、反转驱动拉伸杆前后运动，由于套筒与机架固定，此时侧杆将绕点旋转。拨爪在前后运动的同时将会绕与拉伸杆连接的销轴旋转，这样末端点就有了确定的运动路线。该拨爪机械手对开环多关节机械手进行改进，拨爪和套筒通过侧杆铰接，这样在拨爪与拉伸杆的铰接处省去驱动电机，使拨爪机械手结构简单，节约设计成本；四个拨爪都通过与拉伸杆相连的电机驱动，可以使其动作一致，运动过程更加平稳。

2.2 铰接点分析

所述拨爪机械手的拨爪和套筒通过侧杆铰接，侧杆的铰接点选取要遵循以下原则：（1）侧杆铰接后可以实现机械手拨开和拨回功能；（2）侧杆与拨爪运动过程中不发生干涉现象；（3）铰接点应保证拨爪在较小的驱动条件下实现规定运动。

分析拨爪和套筒铰接位置可以发现，当铰接点位于拨爪上半部分时，其运动过程中会发生干涉，拨爪运动范围受到较大限制，因此铰接点不宜位于拨爪上半部分，如图2所示。

图2 拨爪与侧杆干涉图Fig.2 The Interference Figure of Pull Claw and Side Rod

取杆长相同的拨爪模型，分别将铰接点布置在距离拨爪末端处和处。将Solidworks中建好的模型导入到Adams中，加入同类型约束和相同作用力，如图3（a）、图3（c）所示，其中，Force1=Force2=Force3=Force4=3.9E-003，Force5=88E-003，仿真结果，如图3（b）、图3（d）所示。对比图3（b）和图3（d）可知，在仿真时间相同情况下，铰接点布置于距离拨爪末端时的运动范围大于布置于距离拨爪末端时的运动范围；在同一位置，铰接点布置于距离拨爪末端时的速度、加速度大于布置于距离拨爪末端时的速度、加速度。由此可知，铰接点的选取与末端点的运动有关。在相同运动时间内，铰接点越靠近末端点，其运动范围越大；在运动过程中的同一位置处，铰接点越靠近末端点，其速度和加速度越大。

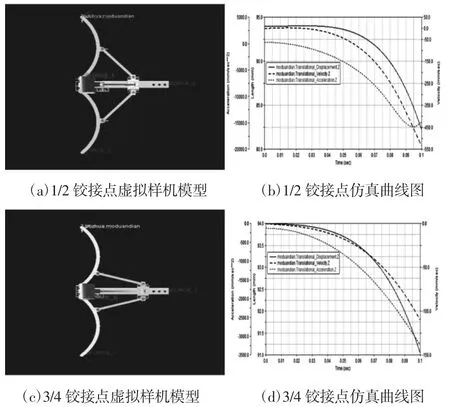
图3 不同铰接点位置虚拟样机模型及仿真曲线图Fig.3 The Virtual Prototype Model and Simulation Curve of Different Hinged Position

2.3 结构尺寸分析

取机械手的部分为例，对其做如下的分析：

图4 结构尺寸关系图Fig.4 The Diagram of Structural Dimensions

图中：A1—拨爪两铰接点与拉伸杆之间角度；A2—侧杆与拉伸杆之间角度；A3—拨爪两铰接点与侧杆之间角度；A4—拨爪两铰接点与拨爪割线之间角度；l1—侧杆长度；l2—拨爪两铰接点之间的长度；l3—拨爪铰接点与套筒铰接点之间的长度；l4—拨爪割线长度。

如图4所示，根据几何关系，可得：

根据（1）式，可得：

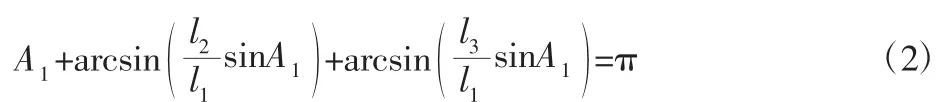
对于具体结构，l1和l2已知，则A1可用l1线性表示，即：

2.4 工况分析

在实际环境中，机械手运动分为拨开和拨回两种工况。

其实际拨回工况条件下，初始螺栓与外盖呈一定角度，机械手四个拨爪极限姿态为：拨爪末端内侧与四个螺栓端面同时接触，其尺寸关系，如图5（a）所示。电机转动后，驱动拉伸杆向后运动，由于套筒固定，因此侧杆绕点旋转。拨爪在前后运动的同时，也绕点旋转，这样末端点就有了确定的运动路线。当末端内侧与螺栓接触后，电机继续转动，直到螺栓与外盖处于垂直。

其实际拨开工况时，初始螺栓轴线与外盖处于垂直，其机械手四个拨爪极限姿态为：拨爪末端外侧与四个螺母内接，其尺寸关系，如图5（b）所示。其电机转动方向与拨回过程中方向相反。

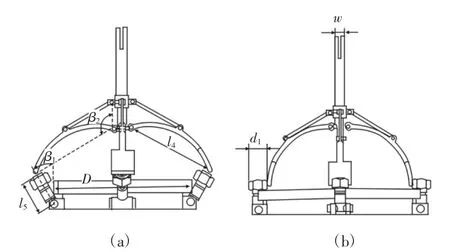
图5 拨开、拨回结构尺寸示意图Fig.5 The Diagram of Dialing and Returning

根据图5，可确定其拨开和拨回两个过程中，各杆件尺寸需满足下面方程组

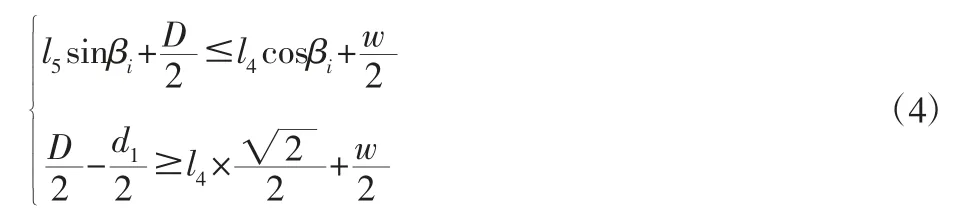
根据式（4），选择一组数据进行仿真验证，各杆件参数，如表1所示。

通过式（4）计算可知l4应满足：168.4mm≤l4≤172.6mm，取l4=171mm进行仿真。

根据表1中各参数，模拟拨回工况下角度β2及z方向位移，建立虚拟样机模型，如图6（a）所示。在模型中拉伸杆末端施加沿x正方向驱动，速度大小设置为10mm/s，其初始值l3设定为98mm。角度β2变化曲线和末端点z方向位移曲线，如图6（b）、图6（c）所示。由图6（b）和图6（c）可知，当β2=120°时，lz=156.5mm≥；当β2=135°时，可以满足方程组（4）的关系，从而验证结论的准确性。

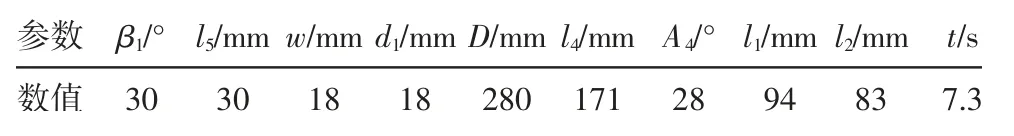
表1 仿真参数表Tab.1 The Simulation Parameter Table

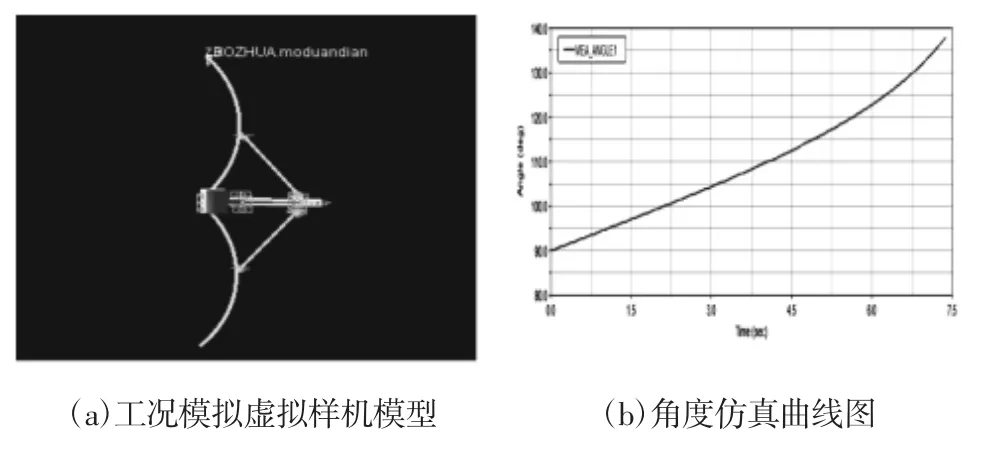
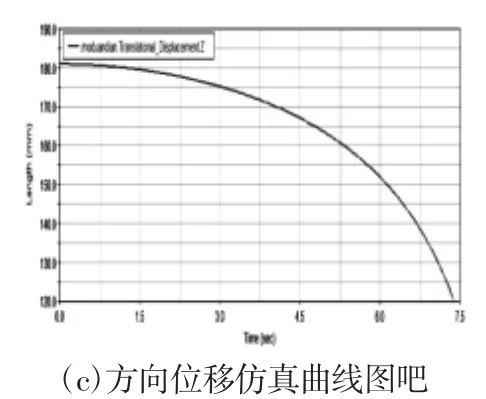
图6 具体工况仿真曲线图Fig.6 The Simulation Curve of Specific Conditions

3 机械手运动学模型分析

3.1 正向运动学分析

运动学研究通常选用DH法，根据机械手的关节类别，建立机器人各关节坐标系，如图7所示。

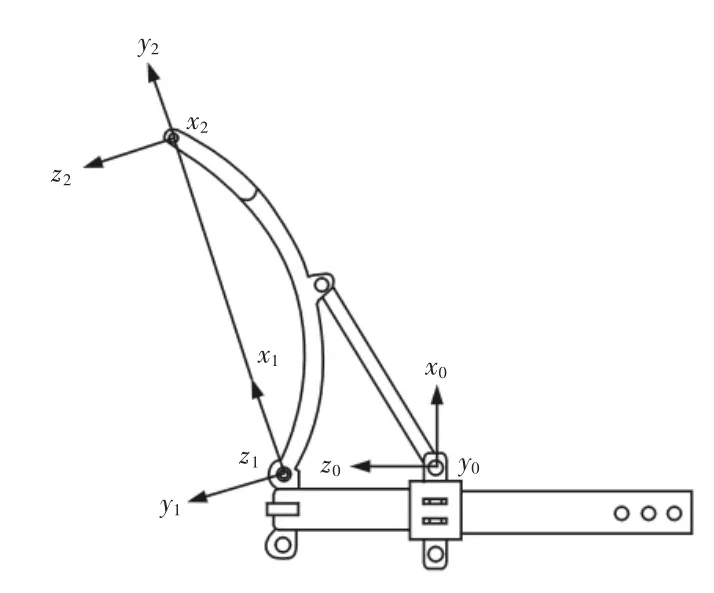
图7 机械手坐标系建立图Fig.7 The Mechanical Manual Coordinate System

图中：xiyizi—关节i的坐标系；z0y0z0—基坐标系。

用以下参数描述连杆，ai—连杆长度，αi—连杆扭角，θi—连杆转角，di—连杆距离，运用齐次坐标变换描述该机器人相邻杆件的空间关系：

z1y1z1系相对于x0y0z0基坐标系的变化为：

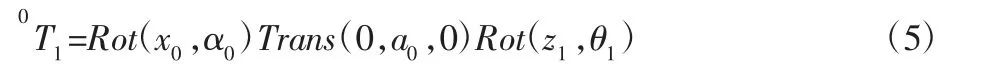
x2y2z2系相对于x1y1z1系的变化为：

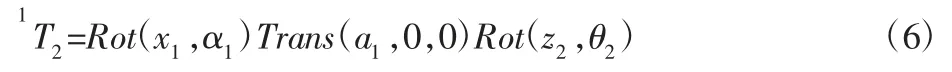
最终可建立x2y2z2系相对于x0y0z0基坐标系的齐次变换矩阵：

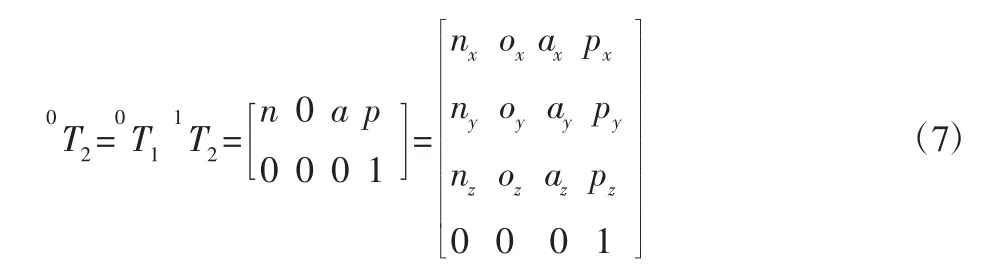
其中，

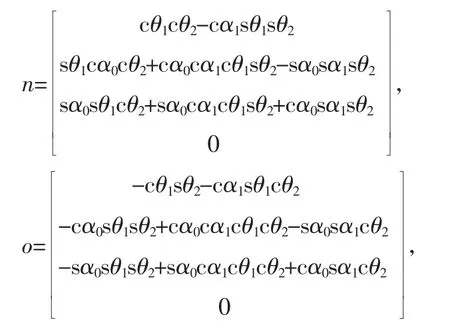
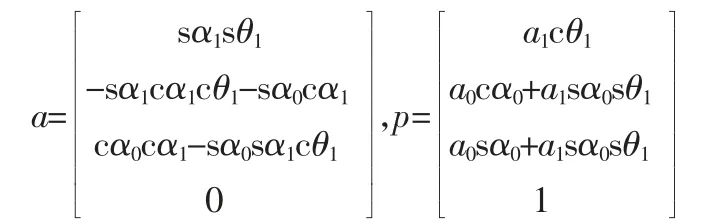
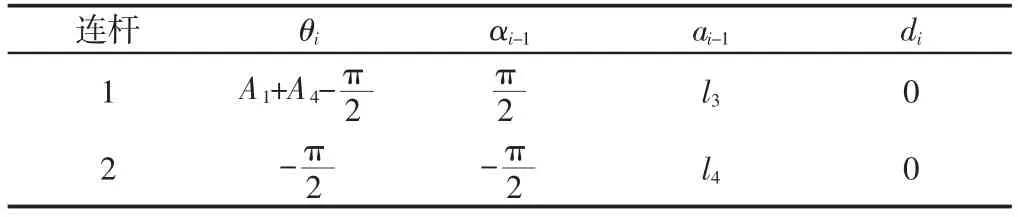
表2 连杆参数表Tab.2 The Linkage Parameter Table

将表2参数带入式（7），得：

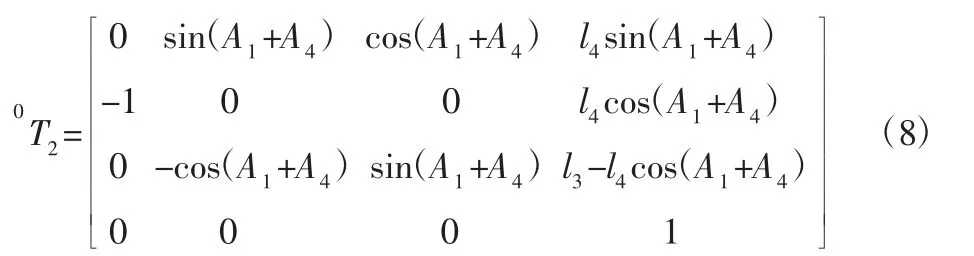
对于具体结构，l4和A4为已知，结合式（3），可得只含一个未知变量l3的机械手末端位姿方程。

3.2 逆向运动学分析

假设末端位姿为：

由式（5）可得：

将表2参数带入，得：

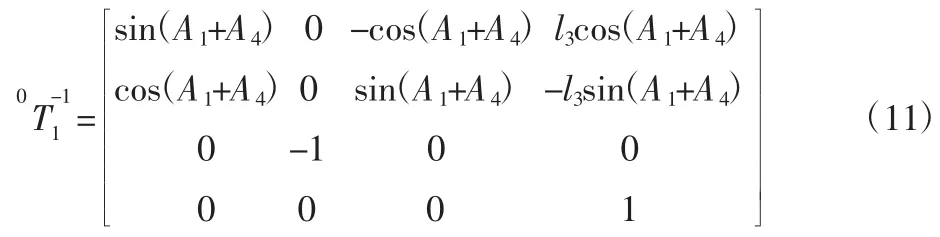
由式（6）可得：

将表2参数带入，得：

由式（7）可得：

将表2参数带入，得：

对于具体结构，式（11）、式（13）、式（15）中，l4和A4为已知，结合式（3），可得只含一个未知变量的机械手末端位姿方程。

令公式两端元素对应相等，可得任意位置的变量。

4 基于Adams的运动学仿真与分析

对拨爪机械手进行数值仿真，仍然采用1.4节建立的虚拟样机模型。由于在实际工况下，拨爪末端点直接与其他部位接触，所以为了研究其工作范围是否符合工作需要，需研究拨爪末端点的运动轨迹。取两个位置相对拨爪，对其之间的距离进行仿真，如图8（a）所示。对机械手末端速度和加速度进行仿真，如图8（b）、8（c）所示，可知其运动是否平稳，是否符合实际工况；对拨爪角速度和角加速度进行仿真，如图8（d）、图8（e）所示，观察其角度变化情况，可以验证其拨爪尺寸及角度设计的合理性。

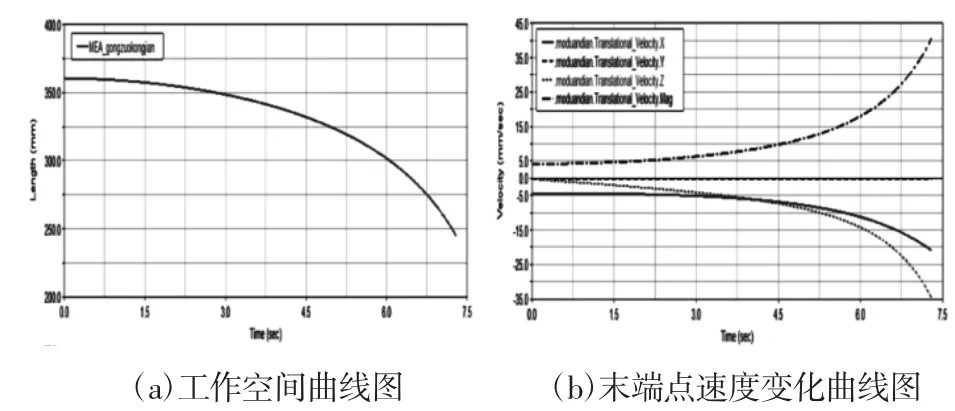
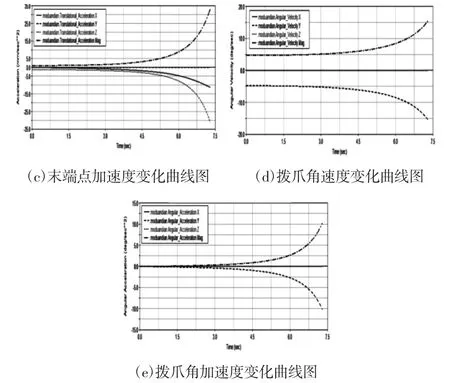
图8 运动学仿真曲线图Fig.8 The Kinematics Simulation Curve Diagram

从图8（a）可知，末端点之间的距离由变为，可大体确定其工作范围。因此在此范围内不应布置其他部件，以防发生碰撞。从图8（b）和图8（c）可以看出，整个过程中速度变化平缓，而且运动过程中没有明显的震颤现象，加速性能较好。速度处于缓慢上升的走势，与实际工况下初始接触拨爪运动较缓慢，随即速度逐渐变大的要求相符。从图8（d）和图8（e）可知，拨爪角速度和角加速度变化平稳，运动过程中无波动现象，基本呈现线性增长，避免了死点角度，说明拨爪的尺寸设计较合理。

5 结论

介绍了一类面向核环境的侧杆式拨爪机械手，对其进行结构分析，通过Adams仿真确定了侧杆铰接点位置与拨爪运动之间的关系；模拟实际工况，建立了拨爪和外盖的尺寸关系模型；提出一种借助结构尺寸关系解决此类侧杆式机械手运动学分析的方法；借助Adams建立虚拟样机模型，对机械手的运动进行仿真。仿真结果表明该机械手有较好的运动特性及较强的实用性，可代替人工实现高辐射极限条件下对滤芯的更换。末端可以进行一定的改造，以适应不同的工况。在仿真计算过程中未考虑关节摩擦力，今后可以对此方面做进一步的研究。