地下水源热泵回灌过程颗粒迁移-脱离模型及堵塞区判定
秦雪滔,蔡宜洲,崔先泽
(三峡大学水利与环境学院,湖北 宜昌 443002)
0 引 言
地下水源热泵是采用地下水作为低位热源,并利用热泵技术,通过少量的高位电能输入,实现冷热量由低位能向高位能的转移,从而达到供冷或供热目的的系统,是取代传统供暖制冷方式最现实、最有前途的技术。该系统运行中如果只取水而不进行有效回灌,可能会造成地面沉降并引发地下管线破坏,因此地下水的回灌广泛存在于地下水源热泵工程中[1-2]。然而,由于回灌水中常携带有细砂颗粒、铁锈及微生物等原生及次生颗粒,并随地下水在含水地层中进行迁移、沉积及脱离,将可能引起含水地层水文地质条件发生改变[3- 4]。该过程一方面会引发回灌堵塞,严重影响地下水源热泵系统的运行效率,另一方面也会引发地层变形,从而危及地面建筑及地下管线安全。因此,地下水源热泵工程回灌水中颗粒迁移沉积过程研究[5- 6]及回灌堵塞区的判定具有重要的研究意义。
国内外关于细小颗粒在多孔介质中的的沉积及脱离过程已有相关研究。S. E. Silliman等[7-11]通过可视化装置追踪孔隙内悬浮颗粒的运移和沉积过程,该理论阐述了悬浮颗粒的局部沉积与颗粒的物理特征、尺寸大小、流体成分和流体速度有关;Derjaguin等[12-13]提出的DLVO理论是最早描述胶体颗粒与多孔介质表面接触的理论,该理论认为偶极子层作用和范德华力是决定悬浮颗粒沉积与脱离最主要的力[14-15],多孔介质中颗粒沉积的最主要沉积原因有滤除作用和吸附作用;陈星欣等[16]利用室内土柱试验研究重力对饱和多孔介质中颗粒输运特性的影响,发现渗流速度越小,重力的作用越明显,多孔介质中沉积颗粒的脱离是由颗粒与多孔介质的接触力及水动力共同决定[17];Bedrikovetsky等[18]建立了考虑拖拽力、静电力、升力及重力的岩石孔隙表面颗粒脱离的模型,该模型可以计算岩石孔隙中颗粒的滞留浓度和过滤系数。
由此可见,国内外在多孔介质中悬浮颗粒的迁移、沉积及脱离已经进行了一些有益的研究,但主要集中于环境工程、化工及石油开采[19]中,且对于颗粒脱离的机制研究较少。本文通过提出的波浪状曲面模型,分析了多孔介质中悬浮颗粒迁移及脱离过程,该模型考虑了不同颗粒及多孔介质尺寸及水动力作用对该过程的影响。随后将该模型应用到典型工况下的地下水源热泵工程中,并对不同抽回灌压力及地层条件下的工程进行模拟分析,提出了回灌堵塞区的分布特征。本研究工作为地下水源热泵工程回灌淤堵研究提供了一种新的思路。
1 颗粒迁移-脱离模型
1.1 基本假设
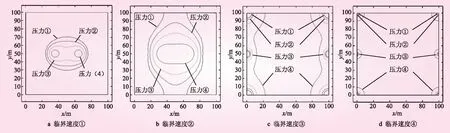
颗粒在地下水作用下起动的方式主要有滑动脱离和滚动脱离两种。影响颗粒脱离壁面的因素很多[20],例如颗粒几何形状、粒径大小、水流速度、温度以及多孔介质的粗糙程度等[21]。本文模型假设颗粒为圆形,主要对颗粒粒径,壁面的粗糙度以及水流速度等影响因素对颗粒的起动及脱离过程进行分析。基本假设为①颗粒为圆形;②多孔介质简化为连续波浪曲线形,且每一段均为半圆形;③颗粒半径r小于波浪曲线形半径R,即r 根据假设建立颗粒迁移-脱离模型,如图1所示。 图1 颗粒迁移-脱离模型示意 在外力作用下,若颗粒能从波浪曲线形多孔介质底端运动至相邻的另一个顶端,即运动中主动力(拖拽力和上升力)做功之和大于阻碍力(重力以及滚动摩阻力偶矩)做功之和,则认为颗粒能够从多孔介质表面脱离。若圆形颗粒能脱离多孔介质表面,则 W拖曳力+W上升力-W重力-W滚动摩阻力偶矩≥0 (1) (2) (3) 拖曳力为[22] FD=γfJV (4) 圆形颗粒在连续波浪形曲线多孔介质中运动时水流拖曳力为[23] (5) 式中,R为波浪形曲线多孔介质的半径;b为圆形颗粒中心到波浪形曲线多孔介质中轴线的距离;v0为波浪形曲线多孔介质内流体轴心速度;v为圆形颗粒的轴向速度。 颗粒受到重力作用的同时,由于浸没在水中又受到水的浮力作用,因此颗粒的有效重度为 Fw=(γs-γf)V (6) 式中,γ为圆形固体颗粒的重度。 上升力为[24] (7) 式中,μ为水的动力粘性系数;ρ水为水的密度;U为平行于壁面的水流速度;Vr为颗粒与水流间的相对流速,当颗粒没有起动时Vr=U。 将式(5)~(7)代入式(3)可得: 图2 临界速度分布 本文通过典型地下水源热泵工程分析不同条件下回灌堵塞区分布特征,井群分布采用常见的一抽一灌模式。计算区域选为边长100 m的正方形,井半径0.075 m。回灌井作为压力入口,圆心坐标为(35,50),抽水井作为压力出口,圆心坐标为(65,50)。模型外边界无流动状态,初始压力设定为2×105Pa。材料系数及数值模拟材料特性参数分别如表1、2所示。 表1 材料系数 表2 数值模拟材料特性参数 计算采用4组压力:①抽水井压力0 ,回灌井压力4×105Pa;②抽水井压力5×104Pa,回灌井压力3.5×105Pa;③抽水井压力1×105Pa,回灌井压力3×105Pa;④抽水井压力1.5×105Pa,回灌井压力2.5×105Pa。根据建立的颗粒迁移-脱离模型,得出4种粒径分布条件下临界速度,结果为①r=5×10-6m,R=2.5×10-4m,临界速度9.3×10-5m/s;②r=1.5×10-5m,R=2.5×10-4m,临界速度3.7×10-5m/s;③r=5×10-6m,R=1×10-3m,临界速度5.4×10-6m/s;④r=1.5×10-5m,R=1×10-3m,临界速度2.1×10-5m/s。在模拟中,若渗流速度小于该临界速度,则认为该位置颗粒将沉积而无法脱离,临界速度所包围的范围即为回灌堵塞区。 图2表示相同粒径组合(相同临界速度)下,4种不同压力分布状态曲线,每一条曲线所包围范围就是悬浮颗粒可以脱离的范围。分析认为,在同一粒径组合(临界速度相同)下,压力越大,压力曲线包围范围越大,可以脱离的悬浮颗粒数量越多。 图3表示不同组合下中轴线速度分布情况,图中不同颜色截线表示不同大小临界速度截线(4种粒径组合),每条临界速度截线与压力曲线相交上半部分范围对应x轴范围表示悬浮颗粒可以脱离的范围。分析认为,在同一粒径组合下(同一临界速度),压力越大,临界速度截线与该压力曲线相交上半部分范围对应x轴范围越大,则悬浮颗粒可以脱离的范围越大。 图3 中轴线速度分布 临界速度②与压力①~④曲线相交范围分别为(26.78,72.88)、(22.82,77.94)、(18.26,81.14)、(16.54,83.61)。压力从压力①到压力④依次增大,从压力①增加到压力②,对应范围增加9.02,从压力①增加到压力④,对应范围增加21。分析认为,相同粒径组合(临界速度)下,压力越大,该截线与压力曲线相交上半部分范围对应范围越大,当压力继续增大时,对应范围也会越大。 由图2、3可知,在相同压力下,临界速度越小,压力曲线包围的范围区域越大,可以脱离的悬浮颗粒区域范围越大。同一压力下,临界速度越小,图中所对应临界速度截线位置越低,该临界速度截线与压力曲线相交上半部分范围区域所对应x轴范围越大,则悬浮颗粒可以脱离的范围区域越大。 压力②曲线与临界速度①~④曲线相交范围分别为(28.27,71.67)、(22.82,77.94)、(6.34,93.86)、(4.56,96.32)。临界速度①到临界速度④依次增大,从临界速度①增加到临界速度②,对应x轴范围增加11.72,从临界速度①增加到临界速度④,对应x轴范围增加48.36。分析认为,压力相同时,临界速度越大,曲线与临界速度截线相交范围越大,当临界速度增大时,对应范围也越大。 图3表示模拟工程场地x轴坐标与渗流速度关系,分析认为,越靠近峰值对应的x轴坐标,曲线越陡峭,渗流速度越大,越远离峰值对应的x轴坐标,曲线越平缓,渗流速度越小。图3中4条曲线分别表示4种不同压力的曲线,分析认为,压力越大,对应渗流速度越大。这表示越靠近两个抽水井和回灌水井,压力越大,渗流速度越大,悬浮颗粒越容易脱离。 本文以地下水源热泵工程为依托,提出了描述颗粒迁移-脱离过程的波浪状曲面模型,通过Comsol模拟得出了不同粒径组合及压力分布条件下回灌堵塞区分布特征,主要结论如下: (1)在相同粒径组合(相同临界速度)下,压力越大,颗粒越容易脱离,回灌堵塞区范围越大。 (2)在相同压力下,当颗粒粒径组合不同时,临界速度不同。临界速度越大,颗粒越不易脱离,回灌堵塞区范围越小。 (3)颗粒所受压力越大,渗流速度越大,颗粒越易脱离,回灌堵塞区范围越大。 (4)距抽水井和回灌水井越近,压力越大,渗流速度越大,颗粒越易脱离,回灌堵塞区范围越大。
1.2 迁移-脱离过程分析



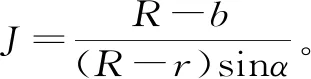
1.3 有效重度
1.4 升力
1.5 颗粒脱离条件

2 数学模型


3 模拟结果
3.1 相同粒径组合下堵塞区分布

3.2 相同压力下堵塞区分布
4 结 论

