松涛水库水温数值模拟研究

方 晴，马剑波，沈文龙，熊 丝，陆宝宏

(1.河海大学水文水资源学院，江苏 南京 210098；2.江苏省秦淮河水利工程管理处，江苏 南京 210022；3.江西省水利规划设计研究院，江西 南昌 330029)

流域内水库的建设会形成流动相对缓慢的大体积水域，使天然河道的水温分布规律发生变化，加上与太阳辐射、入流、出流、库底河床等的热量传输，形成了特有的水库温度场。调节性能强、库水交换周期长的大型水库，沿水深方向多出现分层现象。

国外对水库水温的研究工作开展较早，美国在20世纪30年代便开始了水温监测，并在60、70年代提出了数值模拟方法，使水库水温研究步入了新时代。我国在20世纪50年代起步，对部分水库进行了监测和研究，70年代提出一些经验公式，80年代后引入并改进国外数学模型，开展了大量关于水库水温的模拟研究[1]。但研究区域多集中在亚热带和温带地区，海南等热带地区的水库水温分布规律研究甚少。海南岛属典型的海洋性热带季风气候，太阳辐射强、日照时间长，气温较高且年变幅小，异于我国大多数地区的气候特征。因气候条件是影响水温分布的重要因素，故该地区的水温变化规律与其他地区存在较大差异。

本文以海南省松涛水库为例，采用垂向一维模型模拟了水库的水温分布，分析了该水库的水温结构和坝前垂向水温分布规律，对当地有关部门制定保护措施、进行流域规划的环境影响评价具有一定的科学指导意义。

1 研究区域概况

松涛水库位于海南省南渡江上游段，儋州市和白沙县境内，属南渡江流域(见图1)。控制流域面积1 496 km2，属多年调节大(1)型水库，总库容33.45亿m3，多年平均入库水量14.9亿m3，年库水替换次数为0.45，库面宽阔，平均水面宽2 460 m，最宽处达7 500 m，纵向尺度相对较小，库区流速缓慢，整体形成湖泊型水库。

图1 松涛水库位置示意

2 研究方法

垂向一维模型忽略温度、密度等特性在横向和纵向上的变化，有输入条件简单、计算稳定的特点，对于调节性能较强、水温在横纵向上变化甚微的湖泊型水库，模拟垂向水温效果较好[2]。松涛水库为湖泊型水库，水面宽阔，垂向变化明显，符合一维的假定，故采用垂向一维水温模型——DYRESM模拟水温分布，探究热带地区湖泊型水库水温演变规律。

2.1 模型原理

DYRESM运用拉格朗日分层理论，将水库简化为一个具有多水平层且各层属性一致的系统。模型可模拟、预测水库不同时间尺度的热量特征值，对环境因子和水库属性特征的长期变化进行敏感性检测，已成功应用于多个湖泊及水库的温度、盐度、密度预测[3- 6]。

模型以一维假定为前提，引入湖泊指数LN[7]和地球自转的比率参数R[8]来校核一维假定的有效性。模型运行主要遵守水量平衡、热量平衡两大定律，考虑因水体垂向移流、水气界面热交换、分子和紊动扩散、入流、出流引起的热传递及水体吸收的太阳辐射。

2.2 模型构建

模型需输入地形资料、动力变量、经验参数和状态变量。其中，地形资料包括水库水位-水面面积关系、入流河口处详细情况、取水口、大坝及溢洪道高程；动力变量包括气象条件、入流流量及水温、出流流量等；经验参数多为学者野外观测、实验室试验或率定后确定[9]；状态变量如温度、盐度、水位，用于模型初始化和验证。

2.2.1气象资料

本次模拟时间为2016年3月2日～2017年3月1日，时间步长取一日，故气象数据取日均值或日累积量。气象数据选自距水库最近的儋州气象台站同期观测资料，辐射数据选自同纬度的海口台站同期观测资料。

2.2.2地形、初始剖面资料

地形文件主要输入水库的地理位置和形态特征。

初始剖面资料需输入一组自库底至水面的高度及相对应的水温关系数组。采用松涛水库2016年3月2日实测水温(见图2)作为初始输入资料，由图2可知，水库于3月初已出现水温分层，温跃层厚8.81 m，水温递减率为0.13 ℃/m。

图2 模型输入初始水温分布

2.2.3入、出库流量资料

入库流量选取2016年3月2日至2017年3月1日的松涛水库实测入库资料(见图3a)，其中8月17日～19日和10月13日～19日期间入库流量突增。入流水温为南溪河入库断面处福才水文站多年平均水温。出流资料为松涛水库实测出流过程，见图3b。

2.2.4参数、配置文件资料

根据已有的研究成果及模型经验设置各参数，见表1和表2。

图3 模拟时段内日平均入、出库流量过程

表1 模型参数推荐值

表3 模型率定采用的参数

表4 水温垂向分布特征值统计结果

表2 配置文件参数初始值

2.3 模型率定

DYRESM是一个基于过程的参数化模型，涉及参数较多，且参数具有一定通用性，采用模型默认参数即可得到较满意的模拟结果[9]。研究表明，该模型模拟中小型水库水温结构时精度较高，对于较大、深水库，一些参数需重新率定，如垂向混合系数C、允许最大层厚、最小层厚等[10-12]。考虑到国内应用DYRESM模型模拟水温结构的研究较少，尤其是热带地区，故模型默认参数不一定完全适用，本次基于实测水温数据对参数重新率定。

率定时以模拟值与实测值的绝对误差、均方根误差最小为原则，所有参数在其适用范围内反复调试，最后采用参数值见表3。

采用该组参数对2016年4月26日和6月13日水温进行模拟，结果见图4和表4。

图4 松涛水库水温结构分布

由图4可知，模型基本能反映松涛水库的水温变化趋势和结构特点，两组模拟值与实测水温数据总体吻合，拟合度较好，确定性系数分别为1.00和0.97，均方根误差分别为0.46 ℃和1.25 ℃，最大绝对误差出现于温跃层，分别为1.15 ℃和3.25 ℃。

由表4可知，实测水温与模拟值相比，滞温层的拟合度最高，温跃层拟合度最低。滞温层的温差不超过0.05 ℃，且位置基本吻合；表温层水温模拟值偏高，厚度偏大，但根据已有研究成果[3]，该模拟差异在可接受范围内；模拟的温跃层中心位置上移，温度梯度偏大，4月26日温跃层中心上移2.25 m，温度梯度偏大0.33 ℃/m，6月13日温跃层中心上移0.81 m，温度梯度偏大0.36 ℃/m。

综上，率定后的DYRESM模型模拟效果较好，总体能揭示水库水温分布特征及变化趋势，但模拟结果与实际值仍存在一定差异，且主要存在于温跃层。经分析，产生差异的主要原因为①模拟出的温跃层偏陡是DYRESM模型研究水库水温普遍存在的一个现象[11-13]，有些学者认为可能是模型结构存在一定问题。②DYRESM模型假定消光系数为恒定值，但实际却随时间和水深变化，其取常数时对模拟水温有一定影响[10]。③温跃层深度受内部波运动及昼夜温差的影响，内部波运动会造成温跃层的暂时性偏移。④研究表明[11]，DYRESM模拟中小型水库水温结构效果更佳，因为其水平温度差异性小，易满足一维假定，风应力、热源输入的空间变化对大型水库均会造成水温在水平面上的差异。⑤本文利用的气象资料源于儋州气象站，气象监测数据尤其是风速能否代表湖面实际气象条件存在一定争议[12]。

2.4 模型验证

松涛水库仅有三日实测水温数据，已用于模型输入和率定，且该地区同类型水库水温资料稀缺，故无法移用其他水库验证模型，本文利用松涛水库模拟水位过程与实际水位过程的拟合程度验证模型，见图5。由图5可知，模拟结果的拟合度较高，均方根误差仅为0.18 m，说明模型能较准确地模拟松涛水库水量、水位变化过程，用于模拟该库水温变化是合理的。

图5 松涛水库模拟期内实测、模拟水位过程

3 水库水温结构分析

3.1 经验法判别水库水温结构

采用以下3种经验法初步判别松涛水库的水温结构。

(2)密度佛汝德数法。密度佛汝德数定义为惯性力与浮力的比值，即

(1)

式中，L为水库纵向长度；H为平均水深；V为总库容。松涛水库回水长度约53 km，总库容为33.45亿m3，平均水深51.3 m，多年平均入库流量51.4 m3/s，计算得Fr=0.005 1，可知松涛水库水温结构为稳定分层型。

(3)宽深比法。该方法的表达式为

R=B/H

(2)

式中，B为水库水面平均宽度；H为水库平均水深。松涛水库平均宽度2 460 m，平均深度51.3 m，计算得R=47.95，可知松涛水库的水温结构为过渡型。

综上，不同经验方法得出的结论不同。相比较而言，α-β指数法和密度佛汝德数法综合考虑了水文条件和水库特征，而宽深比法仅考虑了水库的水深和水面宽，故前者更优，且SL278—2002《水利水电工程水文计算规范》[14]推荐使用α-β指数法。但经验法判定水温结构时仅考虑了水库特征、入库径流量，导致判定结果可能有所偏差，而数值模型法理论严密，能较准确地模拟出水库水温的时空变化。

3.2 水温分布年内变化规律

模拟期内松涛水库的水温垂向分布变化过程见图6、7，双温跃层结构如图8所示。

图6 松涛水库模拟期内水温垂向变化过程

图7 水库各月水温垂向分布

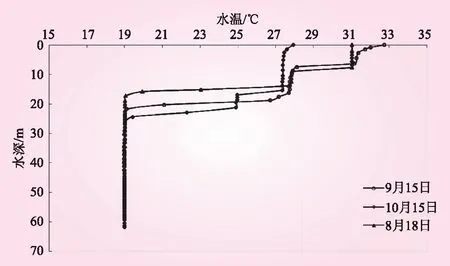
图8 水库双温跃层结构分布

由图6～8可知，松涛水库水温呈显著的稳定分层结构，垂向水温变化有明显的季节性：6、7月平均水温最高，水面最高温度达33.83 ℃；2月最低，库表与库底水体掺混均匀，平均水温19.20 ℃；3月～翌年1月为水库的分层期，2月为混合期；全年内40 m以下至库底水体水温不随时间改变，常年保持在19 ℃左右。

水库水温在年内的具体变化规律为：

(1)升温期。2月份进入升温初期，水温为全年最低，上下层水体由于掺混水温呈均匀分布，垂向温差仅0.40 ℃；3月份随着气温与太阳辐射的逐渐上升，库表开始从外界吸收热量，表层水体水温上升，出现厚度较小(约3 m)、深度较浅、温度梯度仅为0.55 ℃/m的温跃层；4、5月进入升温末期，水体摄入的热能大幅上升，且水库已吸收储存了大量热能，分层强度持续加剧，表层温度升高，同温层厚度增大，温跃层下移，温度梯度达1.7 ℃/m；6、7月气温与太阳辐射达到顶峰，此时温度结构为全年最稳定状态，表层平均水温达33 ℃，温度梯度为1.6～1.88 ℃/m。

(2)降温期。8、9月进入降温初期，水库从外界吸收的热量开始减少，但气温、太阳辐射仍处于较高水平，水温稳定分层，仅表层水温较6、7月略低；8月18日出现双温跃层，19日中部均温层厚度变大，该双温跃层稳定存在至9月20日，此后上层温跃层逐渐减弱，直至10月初完全消失，水库恢复单温跃层结构。10月14日水库再次出现双温跃层，15日中层均温层加厚，至19日达到最厚，此时水库不断向外界释放热量，表层水温逐渐下降，加之中部同温层因入流减少、湍流扩散减弱而逐渐变薄，上部温跃层结构受到扰动，11月5日上部温跃层消失，水库恢复单温跃层结构。随后气温与太阳辐射大幅下降，表层水体冷却加快、密度增加，上层冷水与下层暖水不断掺混，表温层厚度增大，逐渐破坏30 m深的温跃层结构，温度梯度减小，温跃层下移，至1月底该温跃层完全消失，水库恢复上下层水体同温状态。由于该温跃层深度大(水面以下30 m)，而水库水温与外界气温温差逐渐减小，水体向外界散热速率减慢，故该温跃层存在时间长。

图9为模拟期内水库表层水温、入流水温和气温的变化过程，可知全年内三者关系为气温<入流水温<表层水温，不符合水温滞后于气温的规律。可见热带地区的水库水体长时间处于强太阳辐射和高气温的环境下，吸热多，水温常年维持在一个较高水平，同时也反映了除气温外，其他条件如太阳辐射、风速、水汽压、入流水温等也可能会对水温产生影响。

图9 水库表层水温、入流水温与气温变化过程

3.3 双温跃层结构原因分析

松涛水库分别在8月18日和10月14日出现双温跃层，原因分析如下：两次双温跃层的出现均与前一天入库流量(见图3a)猛增有关。模拟期水库的年平均入库流量为68.62 m3/s ，8月17日入库流量1 950 m3/s，入库水温小于库表水温，入流水体沿水库向下潜入与其密度相同的水层，该部分水体紊动扩散能力大，掺混作用强，形成一定厚度的中层同温层，与顶层同温层、下层同温层形成双温跃层结构。8月18日入流流量再次加大，达2 860 m3/s，19日中层同温层厚度进一步增大；同样10月13日、14日、18日入库流量分别为1 280、1 000、4 390 m3/s，造成了10月～11月双温跃层的出现。

两次双温跃层持续的时间不同，前一次持续时间长(约40 d)，后一次持续时间短(约20 d)，其原因可能是8月～10月气温、太阳辐射还处于下降初期，水库散热速率慢，且该时期属流域的主汛期，入库流量较大，中层同温层稳定存在，只能靠表层水体缓慢冷却来破坏双温跃层结构；而10月中下旬后入库流量大幅度减少，中部同温层无法维持强烈的湍流作用，加上水库散热速率增快，故水库双温跃层结构持续时间缩短。

4 结 论

本文以海南省松涛水库为例，采用DYRESM构建垂向一维水温模型，得出以下结论：

(1)松涛水库为典型的分层型，3月～翌年1月为水库分层期，6、7月分层最明显，垂向最大温差达13.90 ℃，8月份进入降温期，水库水体出现翻滚，分层强度开始减弱，1月底分层现象完全消失，2月为混合期。

(2)滞温层水体受环境影响较小，全年保持19.0 ℃左右；库表水温与入流水温、气温的关系为库表水温>入流水温>气温，与其他地区水温滞后于气温的规律不同；模拟期内由于入库流量突然增大，导致水库出现两次双温跃层结构。