基于三元组排序局部性的SOCFS改进算法
吴昌明,赵兴涛,柳可鑫
(中国人民公安大学 信息技术与网络安全学院,北京 102623)
0 概述
在大数据时代背景下,数据维度急剧增长,大量的高维特征广泛存在于模式识别、机器学习、生物信息等领域,如何在高维数据下准确地获取对学习任务有利的信息已成为当前研究的热点。在实际应用中,多数特征是与当前学习任务无关的冗余特征或者噪声特征,这些冗余和噪声特征会给学习任务带来很多不利影响,比如过拟合、低效率。因此,降维成为处理高维数据的重要技术[1]。特征选择[2-3]是当前广泛使用的降维方法[4-5],其在高维数据中选出与当前学习任务相关的特征,去除与当前学习任务无关的冗余和噪声特征,从而降低数据空间维度,便于后续数据处理与任务分析。
在实际应用中,通常需要解决缺少数据标签信息的非监督[6-7]特征选择问题[8-9]。由于数据样本的标签信息未知,因此需要进行聚类,挖掘无标签数据的潜在规律和性质并划分簇结构,从而找到对应的类别。基于不同的特征选择判据以及不同的联合框架,研究者们提出了大量面向聚类应用的特征选择算法,比如拉普拉斯的特征得分法(LS)[10]、非负谱分解的判决性特征选择法(NDFS)[11]、同时正交基聚类特征选择法(Simultaneous Orthogonal Basis Clustering Feature Selection,SOCFS)[12]等。然而,现有的非监督特征选择方法虽然在实际应用中具有良好表现,但是在聚类性能上还有较大的提升空间。因此,本文面向聚类应用研究非监督特征选择问题,选取与当前学习任务相关且具有局部结构保持性与判别性的特征,并去除冗余和噪声特征,以提升聚类性能。
1 相关工作
近年来,非监督特征选择成为人工智能的研究趋势。早期面向聚类应用的特征选择算法基于某种特定的判据,单独评估每一个特征的重要性,从而选择在此判据下的最优特征。此类方法的代表有最大方差法[13]、LS法[14],其中LS法选择对应最大拉普拉斯得分的特征,而相应的拉普拉斯得分可以用来反映局部流形结构的保持能力。然而,单独评估每一个特征重要性的方法不能用于处理多类簇结构。也就是说,对于多类簇问题,很可能不同特征对不同类簇具有不同的判别能力,而单独评估每一个特征的方法忽略了特征之间的组合对类簇的判别作用。因此,文献[15]提出一种面向多类簇应用的非监督特征选择算法(MCFS),其运用谱回归的两步法并联合l1范数最小化进行特征选择。
受联合求解的启发,现有的非监督特征选择算法大多采用一个特定的联合框架来选择最合适的特征子集。NDFS是在一个联合框架中,同时进行非负谱分析和l2,1范数正则化回归,从而实现在整个特征集合中批量选择最具判别性的特征子集。无监督的规范化判别特征选择算法(UDFS)[16]综合了分析和最小化范数以确定特征。然而,UDFS和NDFS算法忽略了噪声和异常值的影响,鲁棒性较差。因此,文献[17]提出一种鲁棒非监督特征选择算法(RUFS),其通过局部学习正则化非负矩阵分解来学习伪标签,同时联合l2,1范数正则化回归进行特征选择,从而有效处理异常值和噪声。SOCFS[12]利用双正交半非负矩阵分解进行正交基聚类,捕捉潜在的类簇中心,从而进一步指导特征选择过程。
上述特征选择方法已经在实际应用中取得了较好的应用效果,但在聚类性能方面依然有较大的提升空间。由于已有特征选择方法忽略了排序局部性对特征选择过程的影响,即特征选择后并不能保持数据点原始的近邻排列顺序,而排序局部性却对基于距离的聚类任务影响较大,因此本文利用数据的三元组局部结构,构建数据之间的排序关系并对该关系在特征选择过程中进行局部保持,提出基于三元组排序局部性的SOCFS改进算法,从而选择排序局部性保持较好的特征,应用于后续的非监督学习任务。
2 SOCFS改进算法
2.1 SOCFS算法
SOCFS是一种非监督特征选择算法。为对无标签数据进行有效的特征选择,该算法设计了一个含有新型目标矩阵的正则化回归公式。目标矩阵通过正交基聚类来捕获映射后的数据点潜在的类簇中心,继而指导映射矩阵选择判别性的特征。SOCFS未使用数据点的局部结构信息作为目标函数的附加项,而是在提出的目标函数中通过使用具有统一项的目标矩阵指导正交基聚类,直接计算潜在的类簇信息,并且可采用一个简单的优化算法实现目标函数最小化。在多个数据集上的实验结果表明:与现有特征选择算法相比,SOCFS获得了更加有效的聚类结果。

(1)
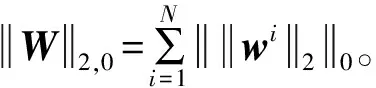

λ>0
(2)

约束的意义为:1)B的正交约束使B的每一列都是独立的;2)E的正交和非负约束使E的每一行都只有一个非零元素。由此可以看出,B作为基矩阵,有正交性,E作为编码矩阵,ET中每一列的非零元素选择B中的一列。该约束确保了SOCFS算法基于距离的正交基聚类。
T=BET使用正交基B和编码矩阵E对映射后的数据点WTX进行聚类,所以T能估计WTX的潜在类簇中心。然后,X经过W的映射后,可以成功逼近由T估计出的潜在类簇中心。由于B的正交约束使得WTX映射后的类簇更加分散(类簇中心相互独立),因此使得W能选择更有判别性的特征。对于E,已有方法通过近似正交约束的方式解决问题式(2)。然而,因为该方法是基于非负矩阵分解,在多数情况下其处理的是非负约束而不是正交约束,且也不能完全保证E是一个正交矩阵,所以E不能作为编码矩阵。因此,SOCFS算法的目标函数为:
s.t.BTB=I,ETE=I,F=E,F≥0
(3)
其中,F是一个辅助变量,并带有一个附加约束F=E,这一步转换的目的是从E中分离出非负约束并将该约束施加到新变量F上。当E保持正交性时,F可以通过约束F=E保证E的非负性。改写问题式(3),得到最终SOCFS算法的目标函数为:
s.t.BTB=I,ETE=I,F≥0
(4)
其中γ>0是一个控制F和E相等程度的参数。
2.2 排序局部性
如图1所示,假设在原始空间(见图1(a))中,数据点x0有4个近邻x1、x2、x3、x4,其中相同颜色表示同一类别,即(x0,x1,x2)属于类别1,x3属于类别2,x4属于类别3,线段长短表示距离远近,距离排序为1→2→3→4。当采用W矩阵映射进行特征选择时,可以看到图1(b)中未经过排序局部性保持的特征在投影之后,排序局部性发生了变化,距离排序变为3→4→1→2,这说明原始空间中数据的拓扑结构发生了变化,在基于距离的聚类中,后续过程将会把中间部分的y0、y4、y2聚为一类,从而导致聚类结果的不准确。本文将经过特征选择矩阵投影到新的空间后,使数据的排序得到保持,也就是保持数据的局部结构,从而得到正确的聚类结果,即y0、y1、y2聚为一类,y4为一类,y3为一类,如图1(c)所示。综上所述,在基于聚类的任务中,近邻之间的相对远近关系也称为排序局部性[18-19],对于特征选择过程极其重要。

图1 排序局部性原理
2.3 三元组排序局部性
对数据点xi,经过特征选择矩阵W的映射后得到所选择的新特征组,记作yi=WTxi,因此有Y=WTX。
基于三元组引导的排序局部性表示若存在一个数据点xi及其近邻组成一个三元组向量(xi,xp,xq),经过特征选择矩阵W的映射后,得到一个新特征组构成的三元组(yi,yp,yq)。如果当dist(xi,xp)≤dist(xi,xq)成立时,则有dist(yi,yp)≤dist(yi,yq)。因此,笔者认为排序局部性,也就是近邻的远近关系在基于聚类的任务中得到了保持。
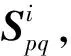
(5)
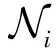

(6)
基于以上数学推导,最终得到保持排序局部性的损失函数为:
(7)

综上,本文得到基于三元组引导排序局部性的损失函数。
2.4 TOL-SOCFS算法
在原有SOCFS算法的基础上,本文加入三元组引导保持排序局部性的附加项Tr(WTXLXTW),得到最终改进算法的目标函数为:

s.t.BTB=I,ETE=I,F≥0
(8)
其中,α是一个标量常数,控制保持排序局部性的损失函数项的相对重要性。
采用交替迭代的方式对式(8)进行优化,并得到基于三元组引导排序局部性的SOCFS改进算法(TOL-SOCFS)。
1)W更新:固定B、E、F求使目标函数值最小的W,与W相关的子问题如下:
(9)
令J(W,B,E,F)对W的导数等于0,有:
α(XLXT+XLTXT)W=0⟹
W=(XXT+λD+0.5αX(L+LT)XT)-1XEBT⟹
W=(XXT+λD+αXLXT)-1XEBT
(10)
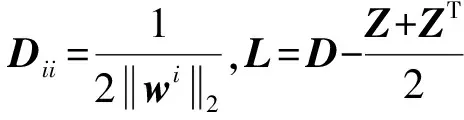
2)B更新:固定W、F求使目标函数值最小的B,与B相关的子问题如下:
(11)

(12)
解析解为:
(13)

(14)
其中,UB和VB分别为矩阵ETXTW奇异值分解后的左右特征向量。
3)E、F更新:固定B和W求使目标函数值最小的E和F,E和F通过固定一个并更新另一个的方式交替迭代。与E相关的子问题如下:
s.t.ETE=I
(15)
子问题可重写为:
XTWWTX)+γTr(ETE-2ETF+FTF)=
(16)
(17)
其中,UE和VE分别为矩阵BTWTX+γFT奇异值分解所得的左右特征向量。
与F相关的子问题可以写为:
(18)
子问题式(18)的解可以改写为:
(19)
算法1为E和F的更新算法,整体优化算法见算法2。由更新规则式(10)、式(14)、式(17)和式(19)可知,目标函数单调下降。
算法1E和F更新算法
输入矩阵Ft、Wt、Bt,参数γ
输出Et+1=E′s、Ft+1=F′s
初始化s=0、F′s=Ft
1.Repeat Step 2~Step 4;
4.s=s+1;
算法2TOL-SOCFS算法


初始化t=0、Dt=I、Bt和Et
1.Construct k-neighbor graph,obtaining Laplacian matrix L;
2.Repeat Step 3~Step 7;
3.Update Et+1and Ft+1by algorithm 1;

7.‖ΔJ(Wt,Bt,Et,Ft)‖≤ε;
2.5 TOL-SOCFS算法复杂度分析

3 实验结果与分析
3.1 实验设置
实验在6个公开数据集上进行K均值聚类[19-21]:目标图像数据集(COIL20),字母读音识别数据集(Isolet1),手写数字数据集(USPS),人脸图像数据集(YaleB、UMIST、ORL)。在每个数据集上,本文提出的TOL-SOCFS算法都与下列5种非监督特征选择算法以及原SOCFS算法进行比较,并且未经过特征选择处理的所有特征被作为对比评估标准[22-23]。
1)无监督的规范化判别特征选择算法(UDFS):基于局部判决得分进行特征选择,其中局部判决得分基于l2,1正则化矩阵反映局部结构信息。
2)面向多类簇应用的非监督特征选择算法(MCFS):基于l1正则化矩阵的谱回归两步法选择特征。
3)非负谱分解的判决性特征选择算法(NDFS):基于非负的谱分析和l2,1正则化回归的联合框架选择特征。
4)鲁棒非监督特征选择算法(RUFS):基于l2,1范数且带有局部学习的非负矩阵分解和l2,1正则化回归的联合框架选择特征。
5)拉普拉斯的特征得分法(LS):先根据算法计算拉普拉斯得分,再选择得分最高的特征,其中计算得到的拉普拉斯得分可以反映特征的局部保持能力。
本文使用聚类精确度(ACC)和归一化互信息(NMI)评估不同算法选择的特征集的聚类结果[24]。对于LS、MCFS、UDFS,NDFS和RUFS,设置近邻参数k的值为5。因为SOCFS和TOL-SOCFS将数据点的局部结构信息嵌入到三元组的损失函数构建中,所以不需要额外设置任何的近邻参数,其中将映射空间的维数m设为潜在类簇的数量c。
针对TOL-SOCFS算法,本文同样采用网格搜索策略在{10-6,10-4,…,104,106}范围内调整所有参数,不同的是相比其他非监督特征选择算法,TOL-SOCFS算法需要调整更多的参数。对于前5个数据集,设置选择的特征数目为{50,100,…,300}。对于USPS数据集,考虑其特征维数的限制,设置选择的特征数目为{50,80,…,200}。本文对所有实验都重复了20次,每次实验均随机初始化并列出ACC和NMI的平均值和标准差,同时随机初始化NDFS、RUFS、SOCFS等算法的变量。
3.2 结果分析
TOL-SOCFS算法与其他非监督特征选择算法的ACC和NMI的平均值和标准差对比结果见表1和表2,其中最优结果加粗表示,括号内的值为当前结果下对应最合适选取特征的数目。由表1和表2可以看出,TOL-SOCFS算法在6个数据库上都产生了比其他非监督特征选择算法更好的实验结果,并且在所选特征数目较少时,TOL-SOCFS算法也有较好的聚类性能。

表1 TOL-SOCFS算法与其他非监督特征选择算法的ACC对比结果

表2 TOL-SOCFS算法与其他非监督特征选择算法的NMI对比结果
如表1所示,在COIL20数据集上,本文提出的TOL-SOCFS算法具有接近3%的聚类性能提升,表明了TOL-SOCFS算法的ACC聚类精确度较高。可以看出,在COIL20数据集上,TOL-SOCFS算法可以选择更少的特征(即200维),但得到比SOCFS算法300维特征更好的结果,验证了TOL-SOCFS算法特征选择的有效性。此外,在USPS数据集上,TOL-SOCFS算法在110维特征数的情况下,可以得到比200维特征的SOCFS算法更好的聚类结果,验证了TOL-SOCFS算法的有效性。同样地,在互信息NMI的度量指标上,如表2所示,TOL-SOCFS算法取得了所有算法中最好的互信息结果,并且在COIL20数据集上,仅通过200维特征即可获得比其他算法300维特征更好的聚类性能,进一步验证了TOL-SOCFS算法的有效性。以上结果主要得益于三元组引导的排序局部性对原始数据拓扑结构的保持,即原始数据中近邻的相对远近关系与数据原始几何结构得到保持,有利于选择具有局部结构保持性及判别区分度高的特征。因此,实验证实TOL-SOCFS算法的聚类性能优于现有非监督特征选择算法。
3.3 算法收敛性分析
TOL-SOCFS算法的收敛性曲线见图2。在6个数据集上的实验结果表明,TOL-SOCFS算法可以在60次迭代内实现收敛,表明其具备快速收敛能力。

图2 TOL-SOCFS算法的收敛性曲线
4 结束语
本文提出一种基于三元组排序局部性的SOCFS改进算法(TOL-SOCFS),利用数据的三元组局部结构,构建数据之间的排序关系并对该关系在特征选择过程中进行局部性保持,从而选择排序局部性保持较好的特征,用于后续的非监督聚类任务。在6个公开数据集上的聚类实验结果表明,TOL-SOCFS算法具有比其他非监督特征选择算法更好的聚类性能,验证了其有效性。鉴于TOL-SOCFS算法利用三元组排序局部性在样本维度上保持映射前后的一致性能力,下一步将更多关注三元组排序局部性在特征维度上的映射保持关系,通过保持映射前后特征的相似性,进一步提升非监督特征选择算法的整体性能。

