二元经济的增长模型分析

陈学信

(广西壮族自治区贺州市交通运输局,广西 贺州 542899)

一、引 言

二元经济结构是一个普遍存在的经济现象,也是我国长期面对的一个重大经济问题。我国虽然在二元经济结构中取得了40多年的快速经济增长,但是二元经济结构的经济增长是如何实现的仍然是一个尚未得到全面解答的问题。

经典的二元经济结构理论(Lewis,1954,1972;Fei and Ranis,1964)[1-3]指出,在劳动力无限供给或供给过剩的条件下,一个经济体存在传统部门与现代部门之间的分割,从而呈现二元经济结构(简称二元经济)。随着劳动力从传统部门向现代部门转移,在经过两个“刘易斯拐点”之后,最终将会变成新古典经济学所说的一元经济结构(简称一元经济)。由于经济结构的差异,二元经济增长与新古典经济增长往往被视为两个不同的发展阶段(蔡昉,2015)[4]。然而,学者们广泛地运用新古典经济增长理论来解释二元经济条件下的经济增长,并取得了丰硕的成果,可见二元经济增长与新古典经济增长并不是分割的,而是有机联系在一起的。

基于此,一些学者试图吸收新古典经济增长理论,用来构建二元经济增长模型(陈宗胜、黎德福,2004;姚洪兴、王佳音,2010)[5，6],但是结果并不容乐观。这主要是因为他们没有注意到,新古典经济增长理论忽略了传统部门与现代部门的资本积累差异或储蓄率差异,从而无法全面地解释在二元经济中极其重要的资本积累。虽然有学者(樊纲、吕焱,2013)[7]注意到了两个部门的储蓄率差异,但是他们的模型所得的众多结论都有悖于现实,显然还有待改善。我们的研究发现,现代部门比传统部门多了一个超额储蓄率,而这个超额储蓄率约等于现代部门的超额技术进步率。在这样的情况下,二元经济的资本积累不仅是储蓄率的增函数,还是技术进步的增函数。因此,二元经济的资本积累方程不同于一元经济的资本积累方程,从而二元经济的增长方程也不同于一元经济的增长方程。

二、二元经济的资本积累方程分析

在二元经济中,传统部门与现代部门的储蓄率是有差异的,这将对资本积累产生重大的影响。为此,我们需要建立一个新的资本积累方程。

(一)二元经济的资本积累方程:基本形式

刘易斯(1954)认为,在二元经济中,工资仅仅能够维持生计,工人们并没有什么储蓄,因而资本积累主要依靠利润的再投资。他说：“经济发展的关键是了解资本家剩余的使用。资本主义部门由于把剩余再投资于创造新资本而扩大,并吸收更多的人从维持生计部门到资本主义部门就业。剩余越来越多,资本形成也越来越大,而且这个过程要一直继续到剩余劳动力消失为止。”[1]12他还指出：“实际上所有的储蓄都是由获得利润和地租的人们进行的。工人的储蓄非常少。中等阶级储蓄一点儿,但是,实际上每个社会里,中等阶级薪水中很少成为生产投资。……储蓄的主要来源是利润,而且,如果我们发现按国民收入的比例来说,储蓄增加了,那么,我们就可以理所当然地认为,这是因为在国民收入中利润的份额增加了。”[1]16-17

平心而论,刘易斯的观点依赖于“工资铁律”的假定,它只适用于资本主义原始积累时期。在现实的二元经济条件下,工资率随着经济发展而不断地上升(李文溥、熊英,2015,2015)[8，9],因而工人也可能进行大量的储蓄,从而资本积累不完全依靠企业的利润再投资。我国自改革开放以来一直处于二元经济结构之中,但是居民的储蓄率居高不下,就是典型的例子之一。但是刘易斯的观点并不完全错误,因为在现代经济生活中,企业的利润再投资仍然是资本积累的主要方式之一。

与刘易斯二元经济理论不同的是,新古典经济增长理论假定投资全部来源于工人即消费者的储蓄。因此,新古典经济增长理论将资本积累方程写作:

(1)

式中:Y为产出;K为资本存量;s为储蓄率;δ为折旧率。

式(1)右边的第一项表示总投资,它表示在一个封闭经济中,储蓄总是等于投资(相当于工人/消费者把自己的全部储蓄借给企业用于投资生产),而且投资全部转化为资本积累。其前提是,假定工人/消费者的总收入等于总工资与总利润之和,即Y=wL+rK;并且假定工人/消费者总是按照总收入的一定比例进行储蓄。

很显然,上述第一个假定是不现实的。首先,工人的投资通常只占总投资的小部分,因而工人只能获得总工资和小部分总利润,其余大部分总利润归企业所得;其次,根据凯恩斯的边际消费倾向递减规律,储蓄率是人均收入的增函数,因而工人的收入水平低于企业,他的储蓄率也将低于企业。为此,我们参照卡尔多(Kaldor,1956)[10]的收入分配模型,假定工人和企业分别获得总工资和总利润,并且假定企业的储蓄率比工人的储蓄率多了一个超额储蓄率,则资本积累方程应改写为:

(2)

式中:L为劳动投入;Δs为企业的超额储蓄率;w为工资率;r为资本回报率或利率。

式(2)是二元经济的资本积累方程的基本形式,它比新古典的资本积累方程多考虑了资本回报率和企业的超额储蓄率。从式(2)可以看出,在刘易斯二元经济条件下,即使工人的储蓄率s为零,但是在企业的超额储蓄率Δs即利润再投资的支持下,资本也能够源源不断地积累。

(二)二元经济的资本积累方程:技术形式

现在的问题是,在现实的二元经济条件下,企业的超额储蓄率由什么因素决定呢?为了回答这个问题,我们首先参照凯恩斯的绝对收入假说,把储蓄函数写作:

S=-C0+bY.

(3)

式中:S为总储蓄;C0为收入为零时的负储蓄或正消费;b为边际储蓄倾向。

上式两边除以收入即产出,可得储蓄率为:

(4)

式中:y为劳均产出;c0为收入为零时的劳均负储蓄或正消费。

令上式右边的第二项等于广义恩格尔系数,也就是令收入为零时的负储蓄或正消费等于食品等基本生活支出——因为收入为零时也必须进行食品等基本生活消费,从而食品等基本生活支出总额与个人收入总额的比例就是广义恩格尔系数λ。则上式可化为:

s=b-λ.

(5)

很显然,在二元经济中,现代部门与传统部门(即资本主义部门与维持生计部门)的收入水平存在差异,它们的广义恩格尔系数也存在差异,从而它们的储蓄率也存在差异。为了简化分析,我们进一步假定,在二元经济中,利润全部来源于现代部门;并且假定现代部门与传统部门的边际储蓄倾向相同(均等于1),则超额储蓄率可写作:

Δs=sm-sa=λa-λm.

(6)

其中下标a、m分别代表传统部门和现代部门(或工资和利润,抑或工人和企业)。

将式(6)代入式(2),可得:

(7)

由式(7)可知,在二元经济条件下,传统部门或工人的广义恩格尔系数几乎是100%,而现代部门或企业的广义恩格尔系数远低于100%,所以现代部门或企业的超额储蓄率很高,从而资本积累主要依靠现代部门或企业的超额储蓄即利润再投资。而在一元经济条件下,传统部门与现代部门的收入水平相同,两者的广义恩格尔系数相同,于是就会得到新古典的资本积累方程即式(1)。

毋庸置疑,现代部门的技术总是高于传统部门的技术——现代部门的“现代”主要体现在这里。为了简化分析,我们假定传统部门和现代部门的技术均以一个固定的比率增长,但是后者的比率大于前者的比率。用公式表示为:

Aa=A0ez.

(8)

Am=A0ez+g=Aaeg.

(9)

式中:Am为现代部门的技术;Aa为传统部门的技术;A0为初始的技术;z为固定的技术进步率;g为固定的超额技术进步率。

其次,为了简化研究,我们不像以往的研究那样把土地单独列出作为传统部门(主要是农业部门)的一项要素投入,而是把所有的土地都折算为资本——毕竟现代部门的资本投入也包括土地价值在内。这样一来,我们可以假定在跨过刘易斯第一拐点之后,即劳动力从无限供给变为短缺之后,传统部门与现代部门的劳均资本相同。则两个部门的劳均产出可分别用C-D生产函数写成:

ya=Aakα.

(10)

ym=Amkα=yaeg.

(11)

式中:k为劳均资本存量;α为资本所得在收入中所占的份额。

于是超额储蓄率可以重新表述为:

(12)

根据二元经济理论,传统部门的广义恩格尔系数接近100%,则上式可进一步简化为:

Δs≈g.

(13)

式(13)表明,超额储蓄率约等于现代部门的超额技术进步率。于是二元经济的资本积累方程即式(2)可进一步写作:

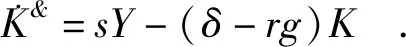
(14)

式(14)是二元经济的资本积累方程的技术形式。由式(14)可知,在二元经济条件下,相对传统部门而言,现代部门的超额技术进步率远大于零,所以资本积累主要依靠现代部门的超额技术进步及其带来的超额储蓄即利润再投资。而在一元经济条件下,相对传统部门而言,现代部门的超额技术进步率为零,结果仍然得到新古典的资本积累方程即式(1)。

三、二元经济增长的稳态分析

二元经济的资本积累方程纳入了技术进步的因素,将会产生很多有意义的结论。下面我们先用它来分析二元经济的稳态问题。

(一)二元经济的索洛图分析

在式(14)两边除以K,然后整理得:

(15)

对劳均资本即k=Y/L关于时间求导,可得各个增长率之间的关系为:

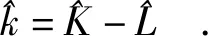
(16)

其中帽子“＾”表示增长率。令劳动增长率等于不变的人口增长率n,则将式(16)代入式(15),可得:

(17)

式(17)的变化如图1所示,它就是二元经济的索洛图。与新古典的索洛图相比,主要区别在于二元经济索洛图的技术进步率的前面是负号,而新古典索洛图的技术进步率的前面是正号。究其原因,是因为新古典经济增长理论强调劳动增强型技术进步(Lucas,1988;Romer,1990;琼斯,2000)[11-13],而本文强调资本体现式技术进步(Kaldor,1957;Solow,1960;Greenwood 等,1997)[14-16]。事实上,技术虽然内生于研发劳动,但是大多融入资本之中并成为资本体现式技术,它与资本是不可分割的。从另一个角度看,生产函数不只有Y=F(K,AL)的劳动增强型的形式,还有Y=F(AK,L)的资本体现式的形式(Barro and Sala-i-Martin,2003)[17],而后一种形式往往更为重要。特别地,在二元经济的条件下,资本相对稀缺而劳动相对充裕,因而技术偏向于资本而不是劳动。

总之,在大部分技术都是资本体现式技术的情况下,我们就能够得到图1的结果。这里应该指出,Romer(1990)[12]推导的只有劳动增强型技术进步的新古典生产函数虽然具有一定的微观基础,但是由于忽略了资本体现式技术进步,将会产生这么一个结论:技术进步将会导致劳均资本的收缩或资本产出比的下降。这个结论通常是脱离现实的。一个典型的事实是,随着计算机技术的持续进步,各国的劳均资本总是不断地扩张而不是不断地收缩。

图1 二元经济的索洛图及其变化

在图1中,从原点出发的曲线sy是劳均资本的正增量曲线,而从原点出发的直线(s+δ-rg)k是劳均资本的负增量曲线,两条曲线的交点就是资本积累的“稳态”,它表示劳均资本保持不变的状态(如G点所示)。当技术进步时,负增量曲线向右下方旋转,劳均资本将会增大(如H点所示);而当储蓄率增大时,正增量曲线向左上方旋转,劳均资本也将会增大(如G′、H′点所示)。总的看来,不仅储蓄率的增大有利于资本积累,技术的进步也有利于资本积累。

(二)二元经济的稳态条件分析

在稳态的条件下,式(17)等于0,则有:

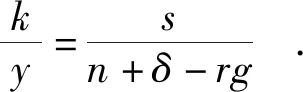
(18)

C-D形式的总量生产函数为:

y=Akα.

(19)

式中:A为中性技术或总量技术。

联合式(18)和式(19),可得稳态的劳均资本和劳均产出分别为:

(20)

(21)

注意式(20)和式(21)的技术进步率的前面是负号,这是与新古典增长理论不同的地方,但却是更符合实际的地方。由式(20)和式(21)可知,技术对劳均资本和劳均产出的影响有两项,而且两项均为正相关,总体上对劳均资本和劳均产出的影响很大。所以,在其他条件不变的情况下,为了提高劳均资本和收入水平,最大的关键是促进技术的进步特别是现代部门的技术进步!

四、二元经济的增长分析

技术进步对于经济增长是非常重要的,但是在二元经济的条件下,劳动力转移也是一个相当重要的因素,而这个因素将会体现在二元经济的增长模型当中。此外,二元经济转型将会带来资本产出比的变化,这种变化也会对经济增长产生影响。下面我们进行具体的分析。

(一)二元经济的劳动力转移和技术进步

总量技术可视为两个部门的技术的几何加权平均值,即:

(22)

式中:ρ为传统部门比重。

对上式关于时间求导,可得总量技术的增长率为:

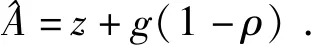
(23)

从式(23)可以看出,总量技术进步不仅依赖于传统部门和现代部门的技术进步,也依赖于传统部门比重的下降,即依赖于劳动力从传统部门向现代部门的转移。其中,传统部门特别是农业部门的技术进步是相当重要的(张培刚,1945)[18],但是在很多情况下,传统部门的技术进步接近于零,从而总量技术进步和经济增长主要依赖于现代部门的超额技术进步。在这样的情况下,在二元经济中,劳动力单纯地从传统部门向现代部门转移,也会提高总体的技术水平,从而促进总体的资本积累和产出增长。不过,劳动力转移本身依赖于现代部门的资本积累,正如刘易斯所说:“二元经济中资本主义部门的就业,总是随着资本形成的发生而扩大的。”[1]45因此,劳动力转移与资本积累通常形成“因果循环积累效应”。

对一个经济体而言,技术进步可能是外生的技术引进或技术模仿,也可能是内生的技术创新。而根据内生经济增长理论,技术进步源于研发部门的创意,以及中间产品部门购买创意后将它转化为资本品,因而它是R&D人员投入的函数(Romer,1986,1990)[12,19]。由此看来,由于R&D人员的创意都转化为资本品,所以R&D人员投入更多地代表了资本体现式技术进步——而更少地代表了劳动增强型技术进步。在这个意义上,内生经济增长理论有一定的自相矛盾之处。

这里值得一提的是,在一个制度不佳的经济体中,R&D人员可能转为生产人员以便谋生,而R&D时间可能用来巴结官僚以便谋利,于是R&D人员投入或经费支出都可能出现下降,从而导致“技术退步”和经济发展停滞。也就是说,制度会通过对技术进步的作用来影响经济增长。因为篇幅限制,具体不再赘述。

(二)二元经济的增长方程

将式(17)略加改写,可得劳均资本存量增长率为:

(24)

式中:β为资本产出比。

对式(19)关于时间求导,可得劳均产出增长率为:

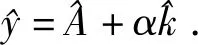
(25)

把式(23)和式(24)代入式(25),可得二元经济的增长方程为:

(26)

这里值得注意的是,资本产出比与折旧率之间有很强的负相关关系(原因是资本存量与折旧率之间有很强的负相关关系),所以折旧率虽然出现在增长方程中,但是它的变化对劳均产出增长率的影响被资本产出比的变化对劳动产出率的影响所抵消,因而折旧率的变化对劳均产出增长率的影响可以忽略不计。从另一个角度看,为了让资本产出比具有可比性,从而让经济增长分析具有可比性,不同的经济体应该使用相同的折旧率。

将式(18)所示的稳态的资本产出比代入式(26),可得稳态的劳均产出增长率为:

(27)

(三)资本产出比及其影响因素

由式(26)可知,在其他条件不变的情况下,资本产出比对产出增长率有较大的影响。当资本产出比过大时,一个经济体可能出现低增长甚至负增长的不利情形(如图2所示)。

图2 世界主要国家的资本产出比与GDP增长率(1970-2014)

注:数据来源于佩恩世界表(PWT9.0;下图同),包含1970-2014年世界68个主要国家(剔除人口少于1000万人的小国,以及5个资本产出比数据异常的国家即赞比亚、刚果民主共和国、哈萨克斯坦、乌克兰和希腊),按资本产出比以0.5为台阶分11组进行统计,然后计算各组的算术平均值。

这里应该指出,新古典经济增长理论认为,沿着稳态的平衡增长路径,资本产出比必定是一个常数。这个观点是有缺陷的。这是因为,资本产出比不变意味着资本的边际收益不变,这就与C-D生产函数的边际收益递减产生冲突。如果边际收益递减是一个必然的规律,那么资本产出比也将呈现边际递减的上升趋势。为了更好地理解这一点,我们将C-D生产函数即式(19)加以修改,就可以将资本产出比表示为:

(28)

由式(28)可知,在其他条件不变的情况下,资本产出比将会随着劳均资本的增长而上升,但是上升的速度递减(如图3所示)。究其原因,主要是因为随着资本存量的增大,资本积累的效率将会越来越低。多马(Domar,1957)[20]早就指出,假定资本产出比固定不变只是为了研究短期问题的方便,这一假定用于长期研究是错误的。

图3 世界主要国家的人均资本存量与资本产出比(1970-2014年)

在现实经济生活中,资本产出比通常随着二元经济转型而持续地上升,这将对劳均产出增长率产生重大的影响。具体而言,当一个经济体处于劳动力无限供给的二元经济时,它的劳均资本很低,所以它的资本产出比将会很小;随着二元经济的转型,一个经济体的劳均资本将会不断地增长,从而它的资本产出比也将不断地上升;当一个经济体发展到一元经济或接近一元经济的阶段,它的劳均资本达到一个很高的水平,从而导致它的资本产出比缓慢地上升并趋于稳定。由此推论,在正常情况下,二元经济的资本产出比低,它的产出增长率将会较大;而一元经济的资本产出比高,它的产出增长率将会较小。这表明处于二元经济的发展中国家可能趋同于处于一元经济的发达国家。

不过我们应该看到,资本产出比是总量技术的减函数,因而在总量技术偏低的情况下,一个发展中国家的资本产出比将会过高,从而导致它的产出增长率过低,进而导致它无法与发达国家趋同。所以,为了控制资本产出比的上升和提高产出增长的速度,从而达到与发达国家趋同的目标,发展中国家必须努力促进技术进步,着力提高资本积累效率。图3的数据表明,2014年我国的人均资本存量仅为50 855美元/人,而资本产出比已经高达4.1;比较而言,2014年美国的人均资本存量高达165 870美元/人,而资本产出比仅为3.2。究其原因,主要是我国的总量技术进步远远落后于美国的总量技术进步,而且我国长期地依赖投资拉动经济增长。在资本产出比已经严重偏高的情况下,为了保证足够高的产出增长率,避免落入中等收入陷阱,我国迫切需要提高技术进步的水平。

五、结语

严格地说,在任何一个经济体中,各个部门的技术进步和收入水平都有所差异,从而存在传统部门与现代部门之间的相对区别。在这个意义上,任何一个经济体都存在二元经济,从而适用二元经济的增长模型。二元经济的增长模型主要是将超额技术进步——即现代部门与传统部门之间的技术进步差异——纳入资本积累方程之中,强调资本积累对技术进步的依赖性,发现了很多有意义的结论。

在二元经济的增长模型看来,资本积累是二元经济转型和经济增长的核心因素,而技术进步在很大程度上是为资本积累铺路的。在这个意义上,技术进步可谓是经济增长的第一要素,即“科学技术是第一生产力”。因此,为了在相对落后的二元经济之中实现持续的、较快的经济增长,我国不能只依靠超常的居民储蓄和资本积累,更要依靠不断的科学创新和技术进步。