最大风速的估算方法与应用

孙 超，汤 超，韩俊杰

（1.黑龙江省太平国际机场气象台，黑龙江 哈尔滨 150001；2.黑龙江省气象科学研究所，黑龙江 哈尔滨150030）

1 引言

风速是指空气质点在单位时间内所移动的水平距离，以m/s 为单位，精度为一位小数。最大风速是指一段时间内出现的最大10 min 平均风速极大值。 极大风速（阵风）是指某个时间段内出现的最大瞬时风速值[1]。 依据《建筑结构荷载规范》中的《全国基本风压分布图》 的风压和运行维护经验估算不同重现期水平的线路基本风压和最大风速是目前国内建筑规划设计施工和电力设计施工单位获取最大设计风速的主要方法。 但是由于以前气象资料站点少，而且没有考虑地形影响，在地形相对复杂、受台风影响频繁的东南沿海地区， 应用这种方法则往往会出现较大偏差。

为此， 在沿海和山地地区最大风速的获取方法与技术方面国内外相关部门单位已经进行了大量研究，并取得了很多成就。 如庞文保、李怀川[2]等人应用经验频率法和P-Ⅲ型分布分析获得15 m 高度的15 a 一遇的最大风速。 庄垂锋[3]曾经利用福州气象站的1953-1982 年的最大风速观测资料分析过福州的最大风速时空分布特征，用极值Ⅰ型分布(即Gumbel 分布) 理论估算福州市不同重现期内可能的最大风速值。 庞文保、白光弼等[4]应用皮尔逊Ⅲ型和极值Ⅰ型分布曲线对陕西省乾县和扶风两个气象站1972-2004 年10 min 平均最大风速资料进行30 a 一遇和50 a 一遇自记10 min 平均最大风速进行极值推断，认为两种方法用于电力部门所需最大风速估算都是可行的。

但是以上这些分析研究都是以地面气象站的实际观测资料为基础展开的。 由于地区内不同气象站的建站早晚以及开始自记风速风向观测的时间不同，开始阶段通常是以每日4 次或3 次定时2 min 平均风速观测记录， 即使在观测气象站有自记风速风向观测记录， 有些年份也存在缺测现象或者因观测站搬迁而受到影响。 因观测高度不同和时次差异须进行相应订正。 订正模式的系统误差以及不可避免的偶然误差都会对计算结果的准确性产生影响。

广东地区处于我国华南南部沿海地区， 地形复杂且易受台风等恶劣天气影响导致大风等灾害。 刘少群，黄泽文，陈丽佳等人曾对广东省的风灾状况展开过调查， 认为导致广东地区风灾的主要原因有热带气旋以及中尺度强对流中的飑线与龙卷， 并给出了相应的风灾防范治理意见[5]。 但目前对该地区的最大风速分布特征以及其极值估算的相关研究分析还较少。 本文使用ECMWF 的REA 分层格点资料对广东及其近海地区风速分布情况进行描述， 统计获得该地区地面以及近地层不同高度上最大平均风速分布特征， 应用皮尔逊Ⅲ型和极值Ⅰ型分布得到本地10 a、20 a、50 a 一遇的最大风速极值，为以后本地的气候状况研究和当地建设规划提供参考。

本文中主要通过对数据的统计分析，总结（18°-26.5°N,108.75°-118.5°E） 地区的不同高度风场的时空分布特征。

应用极值Ⅰ型分布和皮尔逊Ⅲ型曲线两种方法对ECMWF 的多层风场REA 数据资料的不同高度层的年最大风速序列展开分析，并获得各层10 a、20 a、50 a 不同重现水平下的最大风速估计值， 并与初始资料加以比较分析， 总结了这两种方法在实际生产中的应用价值。

2 数据与方法

2.1 数据

初始风速资料是源自ECMWF 的空间分辨率为0.75°×0.75°的 REA 多层 10 min 平均风速格点资料。所取用资料空间为 18°-26.25°N，108.75°-118.5°E 区域，基本覆盖广东省全境以及附近近海地区。 资料为从 1979-2012 年共 34 a 每天 4 个时次的 10 min 平均风速, 再分析资料中距地面高度分别为10 m、30 m、60 m、100 m 四层的平均风速数据，可较好的代表东南沿海地区的最大风速特征。

2.2 研究方法

本文中主要通过对数据的统计分析，总结（18°-26.5°N,108.75°-118.5°E） 地区的不同高度风场的时空分布特征。

应用极值Ⅰ型分布和皮尔逊Ⅲ型曲线两种方法对ECMWF 的多层风场REA 数据资料的不同高度层的年最大风速序列展开分析，并获得各层10 a、20 a、50 a、不同重现水平下的最大风速估值，并与初始资料加以比较分析， 总结了这两种方法在实际生产中的应用价值。

3 不同高度最大风速分布特征分析

3.1 历史最大风速分布特征

文中所研究的区域为华南南部地区， 以及其毗邻的近海海域，空间分辨率为0.75°×0.75°，所占总面积大约8×105km2。 其中陆地主要包括广东省全部和附近的广西东北部、湖南南部、江西南部、福建省西南部以及海南岛。

在研究区域，根据现有资料分别对100 m、60 m、30 m、10 m 四个高度按格点统计获取全风速的最大值， 并绘制了不同高度层1979-2012 年年最大风速变化曲线如下（图1）。

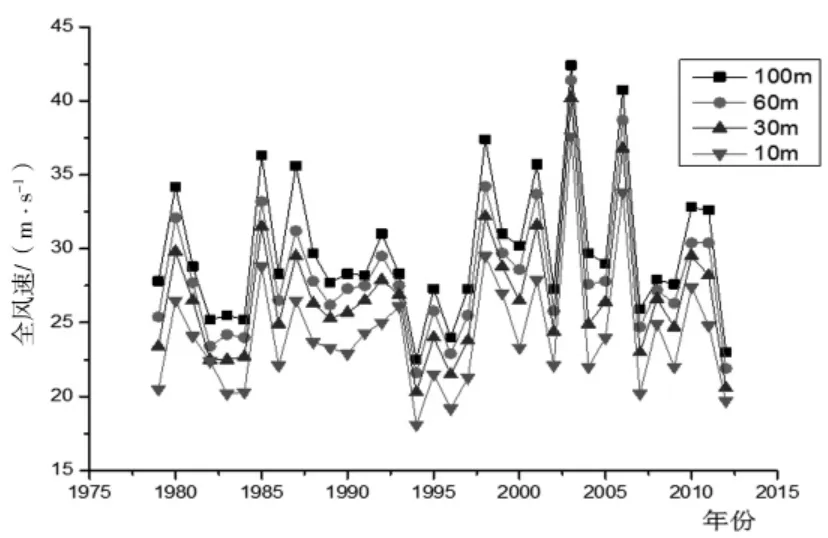
图1 各层年最大风速年纪变化曲线

在研究区域(18°-26.25°N，108.75°-118.5°E)内年最大全风速值从高到低逐渐减小。100 m 高度层的年际差异在22.5-42.5 m/s 之间， 平均年最大风速为29.8 m/s；60 m 高度层的年际差异在 21.6-41.4 m/s之间，平均年最大风速为28.0 m/s；30 m 高度层的年际差异在20.3-40.2 m/s 间， 平均年最大风速为26.6 m/s；10 m 高度层的年际差异在18.1-37.6 m/s 之间，平均年最大风速为24.2 m/s。其中年最大风速的年际极大值出现在2003 年，次大值出现在2006 年；年际极小值出现在1994 年，次小值出现在1996 年。

由图1 可见，在所研究范围内，全风速的年最大值的空间极值有着非常明显的年际变化， 不同高度层的变化趋势十分吻合。 所统计历史范围内，年最大风速的极大值出现在2003 年， 次大值出现在2006年，极小值出现在1994 年。 从曲线的波动情况来看,自2000 年以来曲线波动相对增强，即出现的极大值有所增大。 这充分说明了年最大风速的不确定的特点， 因而需要通过科学的统计以获得在一定时间范围内一遇的可能最大风速。

研究区域内各层最大全风速的极大值均出现在近海的海上， 极小值一般出现在粤北或粤东北的山地地区。 在研究区域内的各个高度层上历史最大全风速有明显的较差（最大值和最小值之差），较差值一般在10-12 m/s 之间。沿海海岸线附近由于下垫面性质的突然变化， 下垫面粗糙度增大， 摩擦作用变强。 风速的梯度最大，从海上到陆地风速迅速减小，从海岸到内陆的狭窄地带内风速能够迅速减小4-6 m/s。从海岸附近的平原和台地向内陆的山区延伸，各层风速也因下垫面性质的改变而减弱。 在近海、沿海岸线以及内陆山区，最大风速有着不同的分布特点。在100 m 高度层上最大风速的极大值与极小值的较差为12 m/s，其中极大值出现在海上，极小值出现在粤北的山区， 而且在海岸线附近风速等值线走向与海岸线相吻合。 在 60 m、30 m、10 m 三个高度层上也有类似的分布特征。

由研究区域历史的年最大风速分布状况， 可将研究区域按照近海、沿海岸线、内陆山地划分为三类区域。 在每类区域内选取两个代表点对其最大风速的分布特征加以分析，并估算该点上的最大风速值。在近海类区域中选择 A （21°N,112.5°E） 和 B (21°N,115.5°E) 为代表点， 在沿海岸线类区域中选择C（21.75°N,111.75°E）和 D（22.5°N,113.25°E）为代表点，在内陆山地类区域中选择 E（24°N，112.°5E）和 F(24°N,115.5°E)为代表点。

3.2 代表点最大风速年内分布特征

为确定年最大风速出现的季节， 须对各代表格点月最大风速的变化趋势进行统计分析。 根据气候统计学的统计规律， 一般在30 a 周期内某地的气候条件一般不会有明显的变化， 所以选择最近1 a，即2012 年各代表格点的月最大风速资料为代表考察研究区域月最大风速的变化规律。

分别对六个代表格点 A、B、C、D、E、F 处 2012 年的月最大风速变化情况统计如下图2：

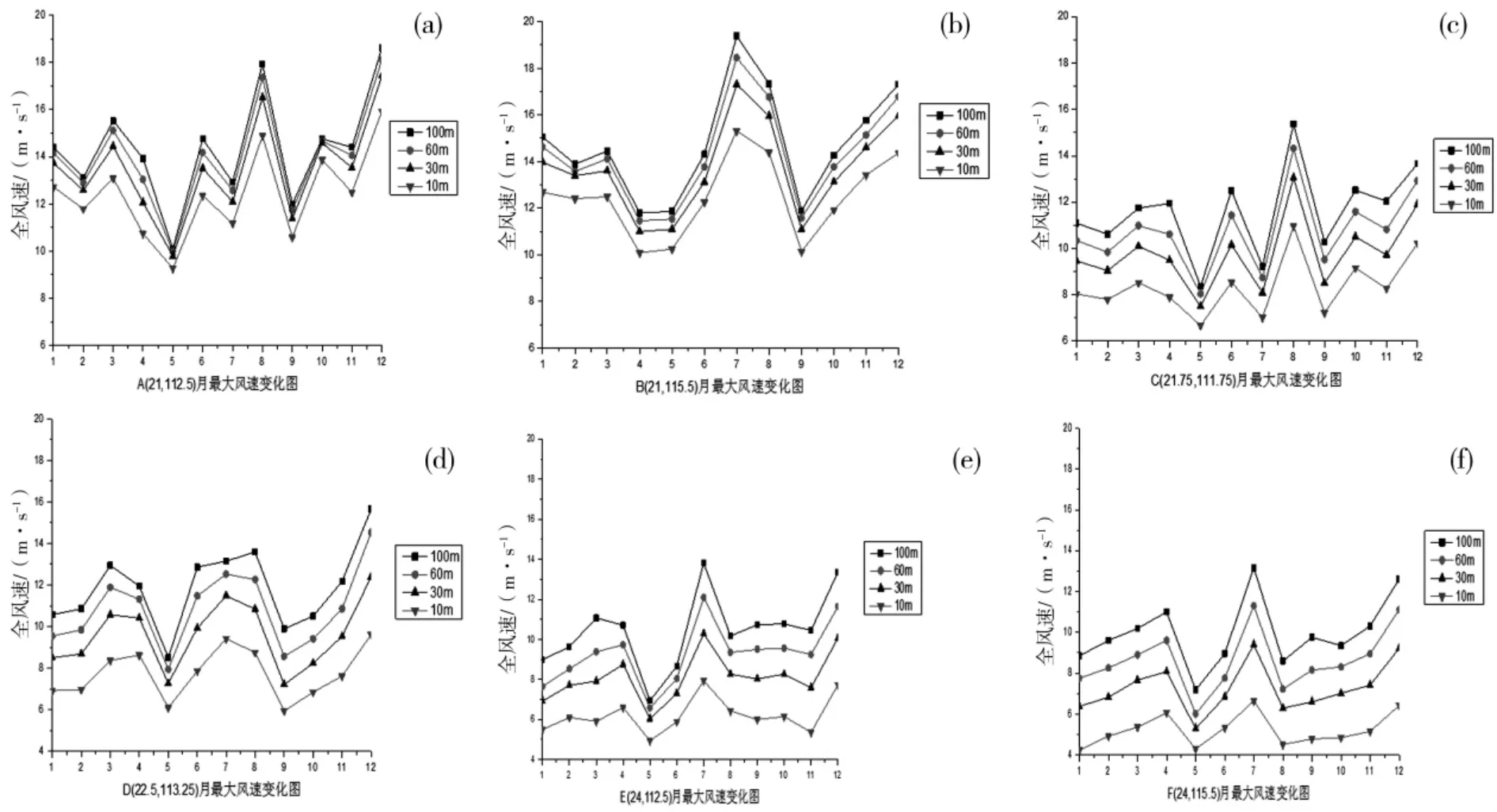
图2 (a)A、(b)B、(c)C、(d)D、(e)E、(f)F 六点 2012 年月最大风速变化

分别分析以上各点月最大风速变化情况可见，在近海类区域代表格点A、B， 其月最大风速的极大值一般出现在7 月或者8 月； 在沿海岸线类区域代表格点C， 其月最大风速极大值一般出现在6、7、8月，即气候意义上的夏季，而D 点月最大风速的极大值出现在12 月份，次大值出现8 月；在内陆山地类区域代表格点E、F，其月最大风速极大值也是出现在7、8 月份， 但相对近海类域其极大值并无明显突变。在所有格点上， 月最大风速的极小值都出现在5 月份、9 月份和10 月份，这与太阳直射点的南北移动而使西太平洋副热带高压控制本地有着必然关系。 夏季的7、8 月份， 是西太平洋副热带高压最靠北的时间，这段时间研究区域位于副热带高压后部，经常会受到来自菲律宾以东太平洋和中国南海温暖洋面上的热带气旋甚至台风的影响。

比较各图可见， 在近海类区域月最大风速的变化情况极为明显，夏季和冬季有明显的突变。 而在沿海岸线类区域次之， 并以内陆山地区域的变化最为平稳。 综合以上月最大风速的分布变化特征，可认为形成研究区域年最大风速值的主要原因是海上的热带气旋及台风， 但是冬季如果有强的冷空气翻越南岭南下也可能形成年最大风速。

4 不同重现期最大风速推算

4.1 极值Ⅰ型分布估算最大风速极值

极值Ⅰ型分布方法是近年来最大风速概率计算以及不同概率下最大风速值极值估算中最常用的方法之一。

根据不同重现水平的概率公式P＝1/R（其中R 为重现水平，以年为单位），可以通过查询极值Ⅰ型ψp值分布表[6]确定 10 a、20 a、50 a 重现水平下的 ψp 值分别为1.3、1.87、2.59。 这种方法中仅有一个参数ψp与被估计最大风速极值的概率相关， 对于某些特定的概率水平计算方法比较简单，易于实现。

4.1.1 100 m 层最大风速极值估算

用第Ⅰ型极值分布方法估算各代表研究点100 m 高度不同重现水平下的最大风速可能极值， 得如下结果。

在表1 中可见， 所选取的各代表点100 m 高度上年最大风速序列的变差系数Cv 在0.10-0.20 之间，其中变差系数最大的是代表近海类区域的A 点，值为0.1890， 变差系数最小的是代表内陆山地类区域的E 点，值为0.1072。 在三类区域中，近海类区域、沿海岸线类区域、 内陆山地类区域的变差系数依次减小， 表明从海上到内陆山地区域年最大风速序列的相对变动程度依次减小， 即年最大风速序列从近海到内陆的波动逐步减小。

根据第Ⅰ型极值分布估算得到的研究代表点10 a 重现水平下的最大风速极值介于16-28 m/s 之间，20 a 重现水平下的最大风速极值介于17-29 m/s 之间，50 a 重现水平下的最大风速极值介于18-33 m/s之间。 与1979-2012 年的34 a 年最大风速极大值相比较重现水平为50 a 时估算的最大风速极大值与之比较接近。

表2 60 m 高度各代表点极值Ⅰ型分布的最大风速极值估计表

4.1.2 60 m 层最大风速极值估算

用第Ⅰ型极值分布方法估算各代表研究点60 m高度不同重现水平下的最大风速可能极值， 得如下结果。

在表2 中可见，对所选取研究代表点A、B、C、D、E、F 各点60 m 高度年最大风速序列的变差系数与100 m 高度基本一致。10 a 重现水平下的最大风速极值介于14-27 m/s 之间，20 a 重现水平下的最大风速极值介于15-29 m/s 之间，50 a 重现水平下的最大风速极值介于16-32 m/s 之间。所计算各重现期水平下的年最大风速的估算极值相对实际资料统计的年最大风速极大值偏小。

4.1.3 30 m 层最大风速极值估算

用第Ⅰ型极值分布方法估算各代表研究点30 m高度不同重现水平下的最大风速可能极值， 得如下结果。

在表3 中可见，对所选取研究代表点A、B、C、D、E、F 各点30 m 高度10 a 重现水平下的最大风速极值介于12-25 m/s 之间，20 a 重现水平下的最大风速极值介于13-27 m/s 之间，50 a 重现水平下的最大风速极值介于14-30 m/s 之间。所计算各重现期水平下的年最大风速的估算极值相对实际资料统计的年最大风速极大值偏小。

表3 30 m 高度各代表点极值Ⅰ型分布的最大风速极值估计表

4.1.4 10 m 层最大风速极值估算

用第Ⅰ型极值分布方法估算各代表研究点10 m高度不同重现水平下的最大风速可能极值， 得如下结果。

表4 10 m 高度各代表点极值Ⅰ型分布的最大风速极值估计表

在表4 中可见，对所选取研究代表点A、B、C、D、E、F 各点10 m 高度10 a 重现水平下的最大风速极值介于9-23 m/s 之间，20 a 重现水平下的最大风速极值介于9-25 m/s 之间，50 a 重现水平下的最大风速极值介于10-28 m/s 之间。所计算各重现期水平下的年最大风速的估算极值相对实际资料统计的年最大风速极大值偏小。

4.2 皮尔逊Ⅲ型分布估算最大风速极值

最大风速极值作为气候随机变量在数学意义上是不稳定的,但它随时间变化过程在概率上却是稳定的。 最大风速这一气象要素在概率上的分布特征暂时还没有确定。 上文已经利用正态分布的极值Ⅰ型分布这一正态分布模型， 对其随时间变化的概率特征进行了一定分析。 现选用皮尔逊Ⅲ型这一偏态分布模型对其随时间变化的概率分布特征加以分析，并比较两种不同分布模型的特征分析结果， 总结不同分布模型下随时间变化的概率分布特征的异同。同时， 皮尔逊Ⅲ型分布在我国电力部门工程设计的最大风速估计和水文单位洪量分析估计中有着广泛的应用， 是极值估计中应用极为普遍的一种统计分布方法。

4.2.1 100 m 层最大风速极值估算

用皮尔逊Ⅲ型分布方法估算各代表研究点100 m 高度不同重现水平下的最大风速可能极值， 得结果如下表：

在表5 中可见， 根据皮尔逊Ⅲ分布估算得到的研究代表点100 m 高度层10 a 重现水平下的最大风速极值介于16-28 m/s 之间，20 a 重现水平下的最大风速极值介于17-31 m/s 之间，50 a 重现水平下的最大风速极值介于18-34 m/s 之间。与1979-2012 年的34 a 年最大风速序列的极大值相比较， 重现水平为50 a 时估算的最大风速极大值与之比较接近。 但是在近海类区域和沿海岸线类区域中， 估算的极大值相比实际风速序列小2 m/s 左右。

表5 100 m 高度各代表点P-Ⅲ型分布的最大风速极值估计表

4.2.2 60 m 层最大风速极值估算

用皮尔逊Ⅲ型分布方法估算各代表研究点60 m高度不同重现水平下的最大风速可能极值， 得结果如表6：

在表6 中可见，对所选取研究代表点A、B、C、D、E、F 各点60 m 高度年最大风速序列的变差系数与100 m 高度基本一致。10 a 重现水平下的最大风速极值介于14-27 m/s 之间，20 a 重现水平下的最大风速极值介于15-29 m/s 之间，50 a 重现水平下的最大风速极值介于16-33 m/s 之间。所计算各重现期水平下的年最大风速的估算极值相对实际资料统计的年最大风速极大值偏小。

表6 60 m 高度各代表点P-Ⅲ型分布的最大风速极值估计表

4.2.3 30 m 层最大风速极值估算

用皮尔逊Ⅲ型分布方法估算各代表研究点30 m高度不同重现水平下的最大风速可能极值， 得结果如下表：

在表7 中可见，对所选取研究代表点A、B、C、D、E、F 各点30 m 高度年最大风速序列的变差系数与100 m 高度也基本一致。10 a 重现水平下的最大风速极值介于12-25 m/s 之间，20 a 重现水平下的最大风速极值介于14-28 m/s 之间，50 a 重现水平下的最大风速极值介于15-32 m/s 之间。所计算各重现期水平下的年最大风速的估算极值相对实际资料统计的年最大风速极大值偏小。

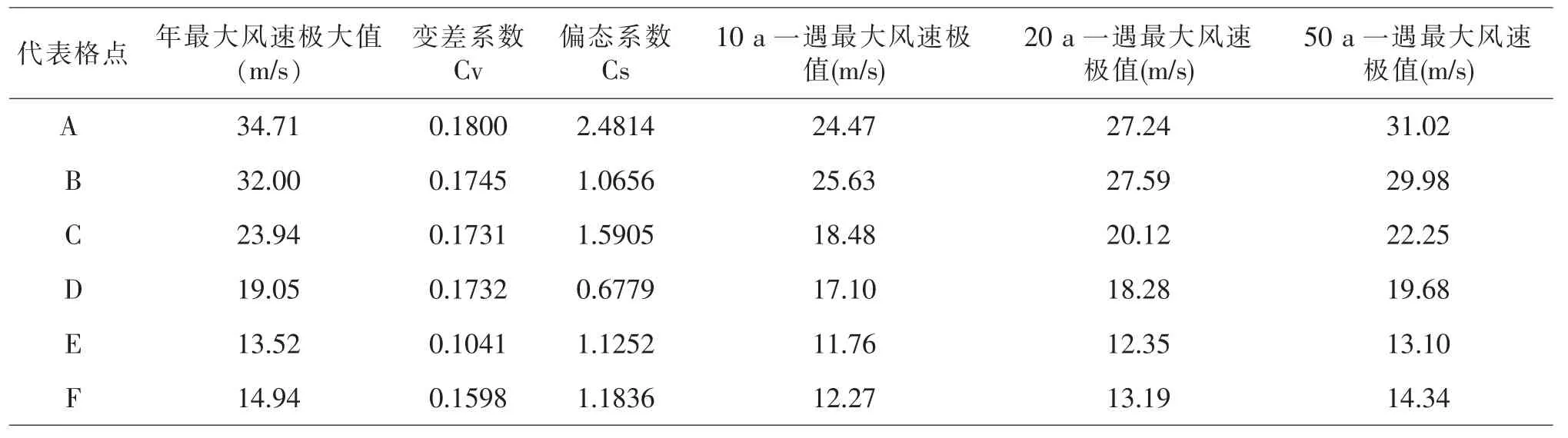
表7 30 m 高度各代表点P-Ⅲ型分布的最大风速极值估计表

4.2.4 10 m 层最大风速极值估算

用皮尔逊Ⅲ型分布方法估算各代表研究点10 m高度不同重现水平下的最大风速可能极值， 得结果如表8：

在表8 中可见，对所选取研究代表点A、B、C、D、E、F 各点10 m 高度年最大风速序列的变差系数与100 m 高度也基本一致。10 a 重现水平下的最大风速极值介于9-23 m/s 之间，20 a 重现水平下的最大风速极值介于9-26 m/s 之间，50 a 重现水平下的最大风速极值介于12-30 m/s 之间。所计算各重现期水平下的年最大风速的估算极值相对实际资料统计的年最大风速极大值偏小。

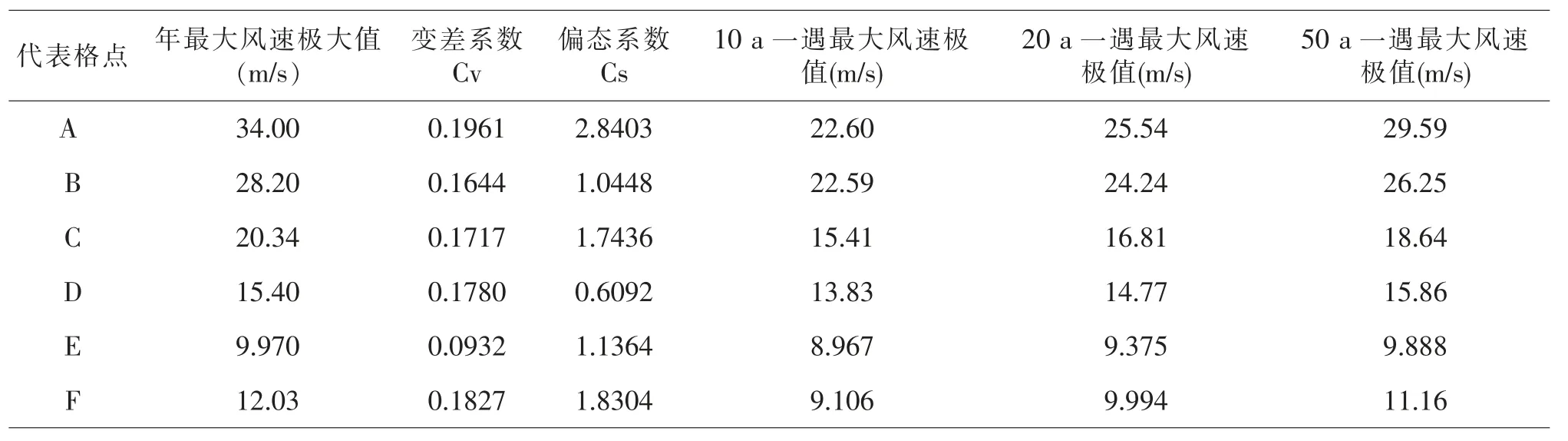
表8 10 m 高度各代表点P-Ⅲ型分布的最大风速极值估计表

4.3 最大风速估算结果的比较

第Ⅰ型极值分布是一种正态分布模型， 皮尔逊Ⅲ型分布是一种偏态分布模型， 两种模型都常用于不同概率水平下某些气象要素极值以及其他要素极值的估算。 两种分布模型因其分布函数与图线不同，故其分布结果也会有差异。

上文中分别利用两种方法对研究区域内六个代表点不同高度层上不同重现期水平， 即不同概率水平下的极大值予以估算。 现就其不同估算结果加以对比分析。

4.3.1 100 m 层最大风速极值估算比较

在100 m 高度层上其最大风速估算结果对比，如下：

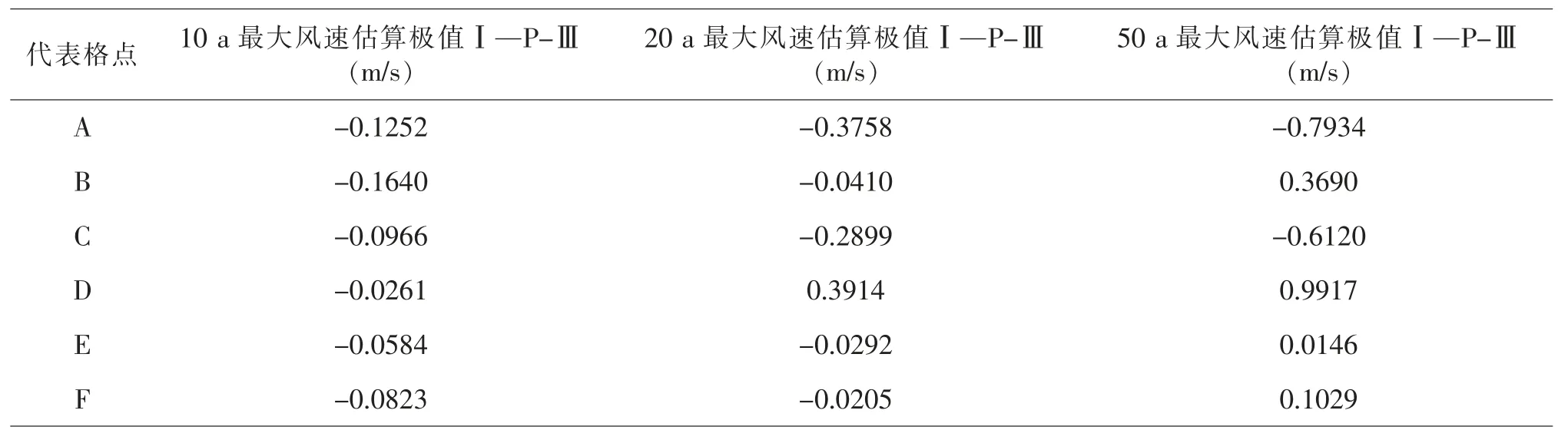
表9 100 m 层极值Ⅰ型与P-Ⅲ型最大估算风速差值

根据表9 中统计数据可见， 两种方法在100 m高度层的最大风速估算应用中， 它们的估算结果有些差异。在重现水平为10 a 条件下，对同一样本的估算中皮尔逊Ⅲ型分布的估算结果要略大于用第Ⅰ型极值分布估算的结果；重现水平为20 a 条件下，大部分统计代表点的估算结果仍是皮尔逊Ⅲ型分布的估算结果要略大于用第Ⅰ型极值分布估算的结果，但在沿海岸线类区域的代表点D 极值Ⅰ型分布的估算结果大于皮尔逊Ⅲ型分布的估算结果； 重现水平为50 a 条件下的估算结果与重现期水平较短的10 a、20 a 结果则相反， 大部分研究代表点的估算结果为第Ⅰ型极值分布的估算值大于皮尔逊Ⅲ型分布的估算结果， 仅有代表近海类区域的A 点和代表沿海岸线类区域的C 点估算结果为第Ⅰ型极值分布的估算值小于皮尔逊Ⅲ型分布的估算结果。

分别对两种方法在近海类区域、 沿海岸线类区域、 内陆山地类区域10 a 重现期水平的估算结果对比， 可见在近海类区域中两种方法的估算结果差值的绝对值最大，沿海岸线类区域与近海类区域类似，内陆山地类区域最小，而重现期水平较长的20 a、50 a 估算结果的差值没有明显的变化规律。比较各类区域不同重现期水平的差值结果， 具有重现期越长差值的绝对值越大的特点， 其中以近海类区域代表点A、B 处最为明显。

4.3.2 60 m 层最大风速极值估算比较

在表10 中可见， 两种方法应用在60 m 高度层的最大风速估算结果有如下差异， 在重现水平为10 a 条件下，对同一样本的估算中皮尔逊Ⅲ型分布的估算结果要略大于用第Ⅰ型极值分布估算的结果；重现水平为20 a 条件下大部分统计代表点的估算结果仍是皮尔逊Ⅲ型分布的估算结果要略大于用第Ⅰ型极值分布估算的结果， 但在沿海岸线类区域的代表点D、F 极值Ⅰ型分布的估算结果大于皮尔逊Ⅲ型分布的估算结果； 重现水平为50 a 条件下两种方法的估算结果各有大小， 其差值在近海类区域的代表点处最大，沿海岸线类区域代表点处次之，以内陆山地类区域代表点处为最小。

表10 60 m 层极值Ⅰ型与P-Ⅲ型最大估算风速差值

但在此高度层上， 同类区域不同重现期水平条件下的差异并无明显规律。在A 点随重现期变长，皮尔逊Ⅲ型分布的估算结果比第Ⅰ型极值分布估算的结果大的差值不断增大，而在B 点则有相反的规律，随重现期变长极值Ⅰ型估算结果相对变大， 而且在重现期为50 a 时超过皮尔逊Ⅲ型分布的估算结果。在相同的重现期水平下， 以内陆山地类区域两种方法的估算结果差值最小。

表11 极值Ⅰ型与P-Ⅲ型最大估算风速差值

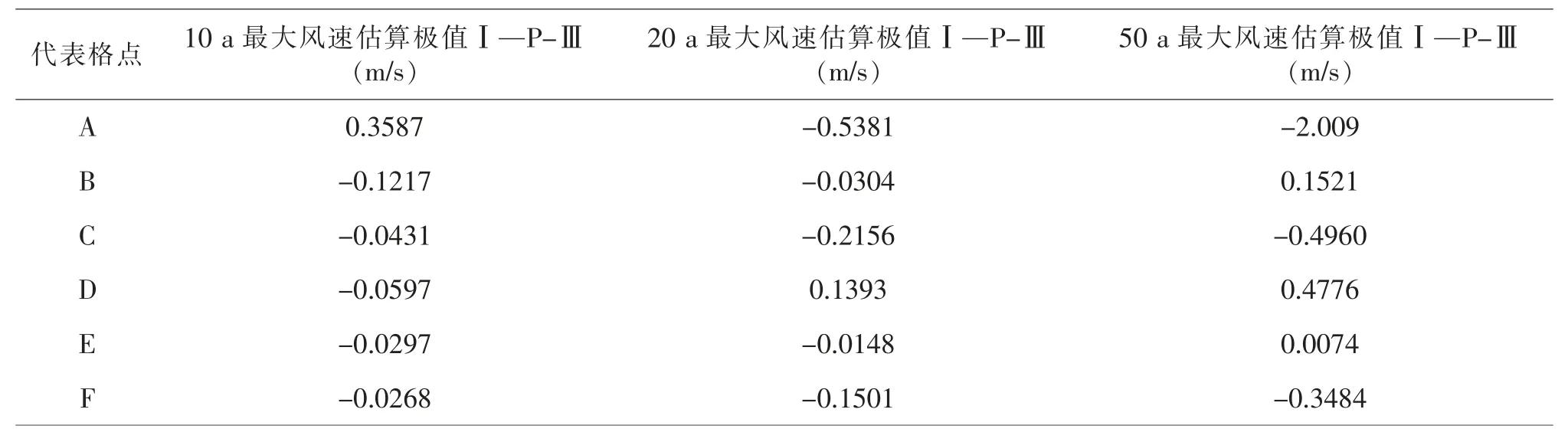
表12 10 m 层极值Ⅰ型与P-Ⅲ型最大估算风速差值

4.3.3 30 m 层最大风速极值估算比较

在表11 中可见， 两种方法应用在30 m 高度层的最大风速估算结果有如下差异： 在10 a 重现期水平条件下， 极值Ⅰ型分布估算的最大风速结果与皮尔逊Ⅲ型分布估算的最大风速结果相比较偏小，仅在A 点极值Ⅰ型分布的估算结果大于皮尔逊Ⅲ型的估算结果；在20 a 重现期水平条件下，极值Ⅰ型分布估算的最大风速结果与皮尔逊Ⅲ型分布估算的最大风速结果相比较偏小， 仅在D 点极值Ⅰ型分布的估算结果大于皮尔逊Ⅲ型的估算结果； 在50 a 重现期水平条件下， 在A、C、F 三点极值Ⅰ型分布的估算结果小于皮尔逊Ⅲ型分布的估算结果， 在B、D、E 三点极值Ⅰ型分布的估算结果大于皮尔逊Ⅲ型分布的估算结果。

4.3.4 10 m 层最大风速极值估算比较

在表12 中可见， 两种方法应用在10 m 高度层的最大风速估算结果有如下差异： 在10 a 重现期水平条件下极值Ⅰ型分布估算的最大风速结果与皮尔逊Ⅲ型分布估算的最大风速结果相比较偏小， 仅在A 点极值Ⅰ型分布的估算结果大于皮尔逊Ⅲ型的估算结果； 在20 a 重现期水平条件下极值Ⅰ型分布估算的最大风速结果与皮尔逊Ⅲ型分布估算的最大风速结果相比较偏小， 仅在D 点极值Ⅰ型分布的估算结果大于皮尔逊Ⅲ型的估算结果； 在50 a 重现期水平条件下， 在A、C、F 三点极值Ⅰ型分布的估算结果小于皮尔逊Ⅲ型分布的估算结果， 在B、D、E 三点极值Ⅰ型分布的估算结果大于皮尔逊Ⅲ型分布的估算结果。

4.3.5 比较结果分析

综合以上对第Ⅰ型极值分布和皮尔逊Ⅲ型分布在各个高度层上差值分布特征的分析可见， 当所取重现期水平较短时极值Ⅰ型分布的估算结果往往大于皮尔逊Ⅲ型分布的估算结果， 所取重现期水平较长时其估算结果差异无明显规律，须具体比较。

在100 m 高度层上两种分布方法所得估算结果的最大差值的绝对值为D 点50 a 重现期水平的差值0.99 m/s，其对极值Ⅰ型分布估算结果的相对差值为4.3%， 对皮尔逊Ⅲ型分布估算结果的相对差值为4.5%；在60 m 高度层上两种分布方法所得估算结果的最大差值的绝对值为A 点50 a 重现期水平的差值1.14 m/s，其对极值Ⅰ型分布估算结果的相对差值为3.6%， 对皮尔逊Ⅲ型分布估算结果的相对差值为3.5%；在30 m 高度层上两种分布方法所得估算结果的最大差值的绝对值为A 点50 a 重现期水平的差值1.69 m/s，其对极值Ⅰ型分布估算结果的相对差值为5.7%， 对皮尔逊Ⅲ型分布估算结果的相对差值为5.4%；在10 m 高度层上两种分布方法所得估算结果的最大差值的绝对值为A 点50 a 重现期水平的差值2.0 m/s， 其对极值Ⅰ型分布估算结果的相对差值为7.2%， 对皮尔逊Ⅲ型分布估算结果的相对差值为6.7%。 所以，两种方法估算结果的差值对于其估算结果而言偏差较小， 特别是内陆山地类区域其相对差值更小，几乎可予以忽略。 所以，两种方法都可应用于最大风速估算。

5 结论

本文通过分析ECMWF 的1979-2012 年的空间分辨率为 0.75°×0.75°的REA 每日四个时次的多层10 min 平均风速格点资料， 提取了研究区域 (18°-26.25°N，108.75°-118.5°E) 空间内的年最大风速序列， 并对其年际变化特征和空间分布特征进行了分析。 在对其空间分布特征进行分析总结的基础上，把研究区域划分为不同类别的次研究区域， 分区选择代表格点统计其年最大风速序列。 分别利用第Ⅰ型极值分布和皮尔逊Ⅲ型分布方法估算了各个代表性格点在不同重现期水平下的最大风速极值， 并比较两种方法估算结果的异同， 分别绘制了最大风速极值分布图。 得主要结论如下：

在研究区域内各个不同高度层上其年最大风速序列的年际变化趋势极为吻合， 最近10 a 以来出现极大风速的频率增加。 100 m、60 m、30 m、10 m 各层年最大风速平均值之差值一般在1-2 m/s 之间。从空间分布来看，因下垫面性质差异，从近海区域、沿海岸线区域到内陆山地区域，最大风速极值依次减小。

以2012 年为代表统计分析了各代表点月最大风速的变化特征与气候成因， 认为年最大风速一般是受热带气旋或台风影响而在夏季形成， 但若是冬季有强的冷空气能够翻越南岭， 在下坡地形作用下也可能出现年最大风速。

第Ⅰ型极值分布是一种正态分布的理论分布。应用第Ⅰ型极值分布估算各个代表格点不同重现水平下年最大风速的极大值随重现期变长而增大，但重现期水平为10 a、20 a、50 a 所估算极大值较年最大风速统计序列中的极大值偏小。

皮尔逊Ⅲ型分布是一种偏态分布的理论分布。应用皮尔逊Ⅲ型分布估算各个代表格点不同重现水平下年最大风速的极大值与应用第Ⅰ型极值分布估算的结果类似。

对比两种不同的分布方法估算最大风速极值的原理与结果。 第Ⅰ型极值分布估算中仅可调整一个参数，即变差系数Cv，在皮尔逊Ⅲ型分布估算中则可以同时调整变差系数Cv 与偏态系数Cs，以更加准确的描述最大风的分布情况， 求得更为准确的最大风速估计值。 两种分布方式在应用原统计样本所得参数进行最大风速极值估算结果比较表明， 在重现期较短时第Ⅰ型极值分布估算所得结果相对皮尔逊Ⅲ型分布估算结果较小，在重现期较长时须具体讨论。但两种方法所估算结果差值较估算值可予以忽略，两种方法均可用于最大风速极值估算， 若能够对计算过程中的参数进行调整得到拟合程度较高的分布曲线， 则可以直接利用分布曲线获得任意重现水平下的极值，而不受参数表限制，将能够更加广泛的应用于计算机估计极值。

本文是在分析ECMWF 的REA 数据的基础上进行的， 仅对最大风速序列的年际变化和月际变化特征进行了分析， 通过简单的分布模式估算了不同重现水平的最大风速极值。 但在分析中没有考虑风向这一重要因素以及地形等因素对最大风速的影响，也没有对分布模式的参数进行调整以更准确的拟合最大风速分布。 未来通过对实测资料分析，调整分布模型的参数，可求得更准确的最大风速估算极值。 综合分析地形等因子对最大风速的影响， 结合风向特征分析可得到更具实用意义的成果。