基于EEMD 与多分辨SVD 的电能质量信号自适应去噪方法

夏 杰

（国网山东省电力公司潍坊供电公司，山东 潍坊 261000）

0 引言

随着电网结构的不断优化和智能化水平的不断提高，新能源、非线性负荷以及其他含电力电子器件的设备大量接入电网，使得多种类型的电能质量问题频繁发生。在工程实际的电能监测与相关处理过程中，所采集到的电力信号通常混有不同程度的高斯噪声，若不对信号进行降噪处理则会导致相关检测精度下降并造成辨识失效，甚至还会导致保护装置的误动作，造成不必要的损失。因此在电能的相关计量之前，对信号进行有效降噪并且充分保留信号的特征信息，对电能质量问题的监测、控制和治理具有重要意义［1-2］。

目前信号去噪中使用较广的方法有经验模态分解（Empirical Mode Decomposition，EMD）、奇异值分解（Singular Value Decomposition，SVD）、小波变换、形态滤波等［3-5］。其中，EMD 分解过程存在的模态混叠问题，使得不同尺度的固有模态函数（Intrinsic Mode Function，IMF）成分相似，对处理的效果影响很大；传统SVD 存在信号重构之后含噪量偏高的问题，且评价指标欠佳；小波变换中的问题则主要表现在小波基的选取，其不具普适性且不同基会在不同程度上影响处理结果；而对形态滤波器去噪而言，变换类型与结构元素的形状尺寸等都是其最终处理效果的影响因素，因此同样存在选取问题。除此之外，由改进的EMD，如集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）、自适应白噪声的完整经验模态分解（Complete Ensemble Empirical Mode Decomposition of Adaptive Noise，CEEMDAN）及其衍生出的通过划分高、低频分量处理噪声的诸多方法中，绝大多数直接舍弃相应高频分量或仅是对高频分量进行处理，而忽略低频分量存在的少量噪声，不进行处理而直接用于重构，同样会在一定程度上影响最终去噪效果，使波形与各评价指标不能最优化。

针对上述存在不足，提出一种集合经验模态分解（EEMD）与多分辨奇异值分解（MRSVD）相结合的改进去噪方法，有效保留原始信号特征、达到良好去噪效果的同时实现了自适应。

1 基本原理

1.1 EEMD 原理

EMD 方法时频分析能力良好，处理过程具备自适应性和正交性，然而其存在模态混叠的问题限制了进一步应用。针对此问题，Flandrin 与Huang 各自的研究小组通过研究寻求了改进，通过对EMD 分解所得结果的数据统计特性进行大量分析研究，提出了通过人为添加噪声进行辅助分析的方法。通过将白噪声加入信号中，以补充一些缺失的尺度，在信号分解过程中具有良好的表现，这便形成了EEMD。其算法具体步骤为［6-7］：

1）在原始信号x（t）中加入一组白噪声信号w1（t），得到总体信号X1（t）为

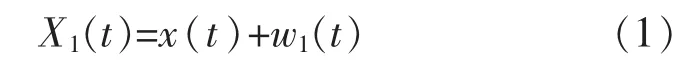
2）对X1（t）信号进行n 次EMD 分解处理，得到各项模态分量c1j（t）及残余分量r1n（t）为

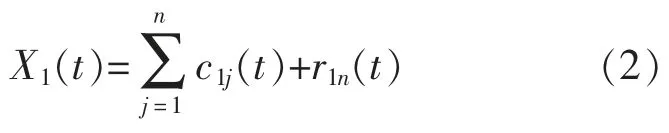
3）在x（t）中加入不同白噪声信号wi（t），i=2，3…并重复以上步骤，得到

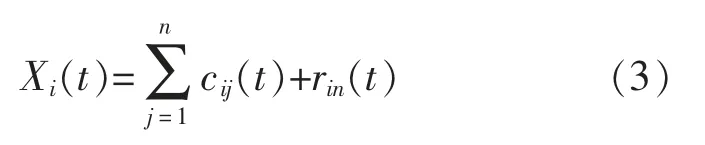
4）将每次处理获得的cij（t）的集成平均值作为最后的处理，结果为

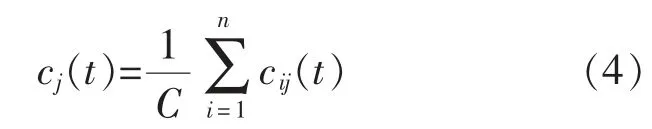
式中：C 为白噪声集成次数，一般取值为100。相比于EMD，EEMD 可以获得更为准确的模态分量。

1.2 多分辨SVD

近年来，奇异值分解（SVD）在数据压缩、信号消噪、特征量提取等方面均得到了广泛应用，但在使用过程中，SVD 方法处理信号所得到的结果在本质上都是处于同一分辨率上的结果，属于同层次的矢量空间。为改进这一缺点，文献［8］将小波分解多分辨的思想应用于SVD，即在SVD 中提出了一种二分递推矩阵构造的方法，称为多分辨SVD 分解（MRSVD）。分解过程如图1 所示，其中Aj、Dj分别代表信号分解j 次所得的近似分量与细节分量。

图1 MRSVD 分解过程

任意一个含噪声信号的采样序列x（l）可表示为

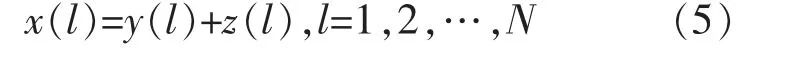
式中：y（l）为有效电能质量信号；z（l）为噪声信号；N 为信号的采样长度。利用此含噪信号x（l）构造的Hankel 矩阵H 为

式中：H1为y（l）对应的矩阵；H2为z（l）对应的矩阵。

在信号的MRSVD 处理过程中，Hankel 矩阵行数取为2，矢量的第2 行数据比第1 行数据仅滞后1个点。对于正常信号，Hankel 矩阵的2 行数据将高度相关，矩阵的秩为1。其奇异值可表示为

式中：ε 为一足够小的正数，而σ1则远远大于ε。从式中可以看出，正常信号的能量被分为了2 部分，其中首个奇异值中占了绝大多数，而仅仅有很微小的一部分信号能量被分配到了另一个奇异值之中。

而对于噪声信号的Hankel 矩阵而言，两行数据不相关，矩阵的秩为2，奇异值彼此大小均匀，可表示为

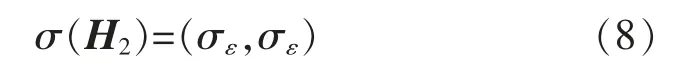
根据矩阵理论，矩阵之和的奇异值有下式成立，即

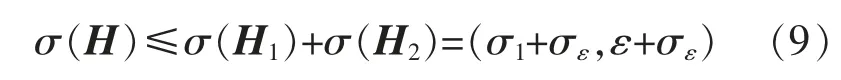
实际上当矩阵行数很小时，式（9）有近似关系成立，即

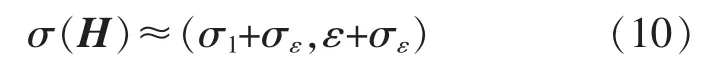
信号能量是与对应奇异值平方的大小成正比的，因此由图1 与式（6）—式（10）可以看出，MRSVD每分解一次，所获得的近似信号Aj中噪声的能量就比上一层Aj-1中有了大程度减少，这种减少的噪声被分离到了细节分量Dj之中；正常信号主体基本被保留在了近似信号之中，而仅有极微小的一部分被分至Dj。当分解达到一定层数时，噪声能量将会被充分分离，从而达到了信号去噪的目的。

MRSVD 分解层数设置的不同会对最终去噪效果产生较大影响，若分解层数设置过少，会使处理不充分，进而影响重构效果与相应评价指标；而层数设置过多，则会增加无谓的计算量。为实现分解层数的自适应性，文献［9］提出一种利用相邻奇异值差值作为停止标准的改进处理方法。

将染噪序列x（l）经过J 次MRSVD 分解后得到的近似分量与细节分量对应奇异值的差值定义为

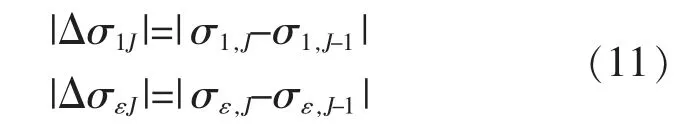
式中：σy，J－1、σε，J－1分别为经过J-1 次分解后得到的近似分量和细节分量奇异值。而随着分解层数的不断增加，差值量｜Δσj｜与｜Δσε｜将会分别形成近似奇异值差值序列B1＝［｜Δσ11｜，｜Δσ12｜，…，｜Δσ1J｜］与细节奇异差值序列B2＝［｜Δσε1｜，｜Δσε2｜，…，｜ΔσεJ｜］。当分解满足以下约束条件式（12）时，则认为近似和细节成分在分解过程中均下降至不再变化，噪声已经得到了充分消除，分解过程终止，最佳分解尺度为J。

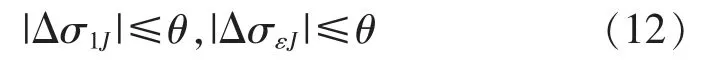
式中：θ 为一很小的随机正整数。

2 基于EEMD 与自适应MRSVD 的去噪方法

文献［10］提出基于EMD 的电能质量信号去噪，将分解后的c1（t）直接舍弃，这样会造成有用信号的丢失，使波形失真，无法体现原有的特征信息；此外IMF 低频分量中同样也含有少量噪声信息，若不进行处理而直接采用，则同样会影响到重构之后的信号波形，使相应评价指标无法达到最佳。若对含噪声信号直接采用传统MRSVD 去噪，不仅计算量较大，随着分解层数的增加，有用信号的损失也较为严重，而且层数选择不具自适应性。因此采用EEMD 和自适应MRSVD 相结合方法进行去噪，选择出含噪量高的高频IMF 进行MRSVD 分解，以充分保留低频IMF 成分中的有用信息，减少运算量的同时降低了有用信息的损失；利用波形相似度指标作为度量选择对重构波形影响程度较高的低频IMF 进行MRSVD 分解，去除其中含有的少量噪声，使重构后波形与各项指标达到最优化。

含噪信号设为

式中：f（t）为原始信号；e（t）为噪声信号。

总体去噪实现步骤为：

1）对原含噪声信号进行EEMD 分解，得到频率由高到低的模态分量cj（t），j＝1，2…。

2）对模态分量高、低频成分进行划分、选择与处理。为实现该去噪方法的自适应性，设定2 个处理原则。

①模态分量高、低频成分界定原则为

式中：M为EEMD分解得到的IMF分量个数；m 为高频分量的个数。

②模态分量的选择与分解原则：设置阈值δ，对高频分量以及波形相似度大于δ 的低频分量进行自适应MRSVD 分解，以充分去除高频成分中含有的主要噪声成分以及保留低频成分中的有效信息。

3）利用分解所得近似分量与未选择处理的低频模态分量进行信号重构，得到最后的去噪信号。

3 仿真分析

电压暂降是电能质量问题中发生频繁和影响范围广的问题之一，因此为了验证本文提出新方法的可行性，通过MATLAB 函数与Simulink 系统分别仿真生成电压暂降信号，进行信号去噪验证。

3.1 MATLAB 仿真

函数相应参数设置如表1 所示。

表1 电压暂降信号模型相关参数

在对原含噪声信号EEMD 分解前的相关参数设置方面，采用的白噪声幅值标准差为0.1，集成次数设为100 次。其信号波形与幅值变化分别如图2、图3 所示。

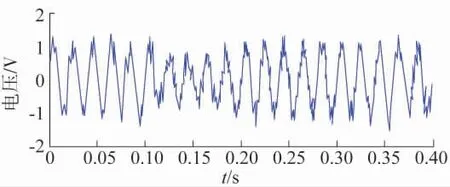
图2 染噪暂降信号（信噪比12 dB）

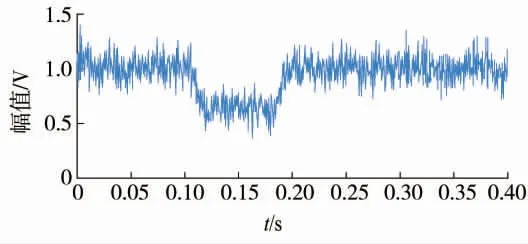
图3 染噪信号幅值

含噪信号的EEMD 分解所得模态分量如图4 所示，其中横坐标表示时间，纵坐标表示各模态分量幅值。从图中可以看出各频率成分被较好的分离，不存在模态混叠现象。

表2 列出了各模态分量与理想信号的相似度，按照前述筛选规则选择可用IMF 分量。划分前3 个分量为高频分量，后6 个分量为低频分量；设定阈值δ=0.025，选择高频分量与低频分量中的c4（t）、c5（t）、c7（t）、c8（t）分量为待处理成分，用于后续分解。

对待处理模态分量进行自适应MRSVD 分解。设置高频分量停止判别阈值θ1=0.03，低频分量判别阈值θ2=0.05 得到分解层数所对应的近似分量Ai，结果如表3 所示。去噪处理后的效果如图5、图6 所示。

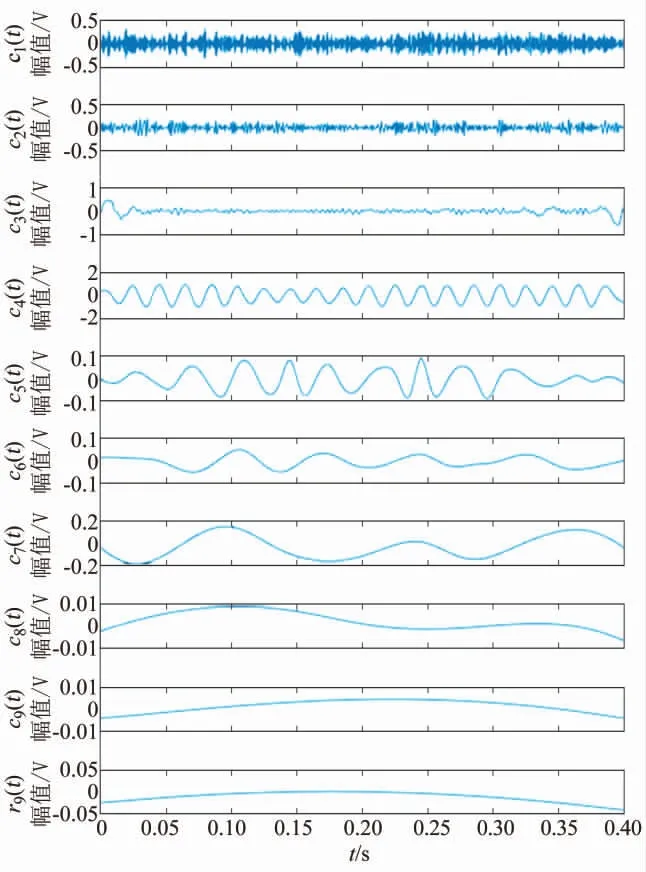
图4 EEMD 分解

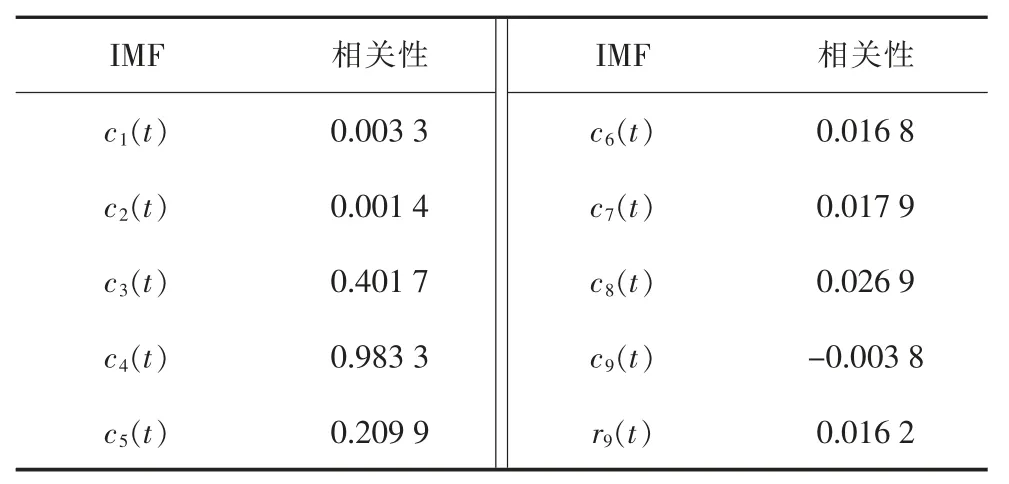
表2 模态分量相关性值

表3 信号去噪结果

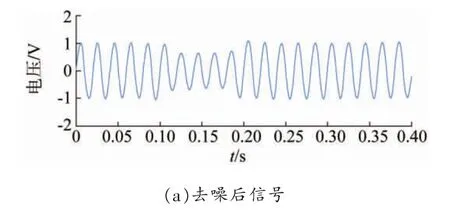
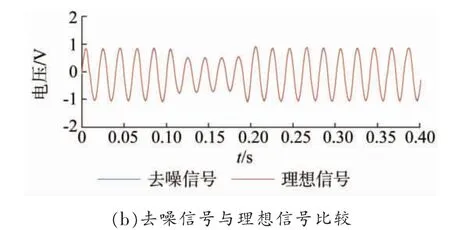
图5 去噪效果（信噪比12 db）

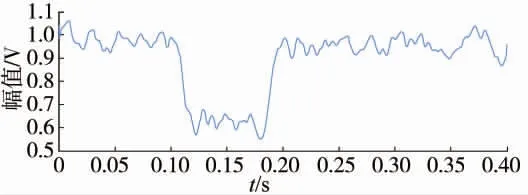
图6 去噪后信号幅值

由图5 可知，去噪后波形平滑，无波形畸变；由图6 可知，去噪后有效保留了暂降特征，效果良好。

为进一步验证所提去噪方法的有效性，对不同噪声程度下的电压暂降信号去噪，利用均方误差XMSE、信噪比XSNR以及波形相似系数XNCC等评价指标来衡量去噪效果好坏。XSNR指去噪信号功率与噪声信号功率的比值，其值越大则去噪效果越佳。XMSE指去噪信号与真实信号差值的平方与采样点数的比值，越低去噪效果越好。XMSE和XSNR从宏观上衡量去噪效果，而XNCC则从微观上体现去噪前后波形变化程度，其值越接近1 说明去噪后波形越接近原始信号。上述3 项指标计算公式为：

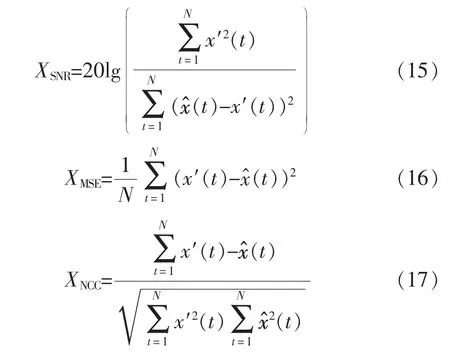
MATLAB 信号去噪过程中不同环境下的分解层数以及去噪指标如表4、表5 所示。

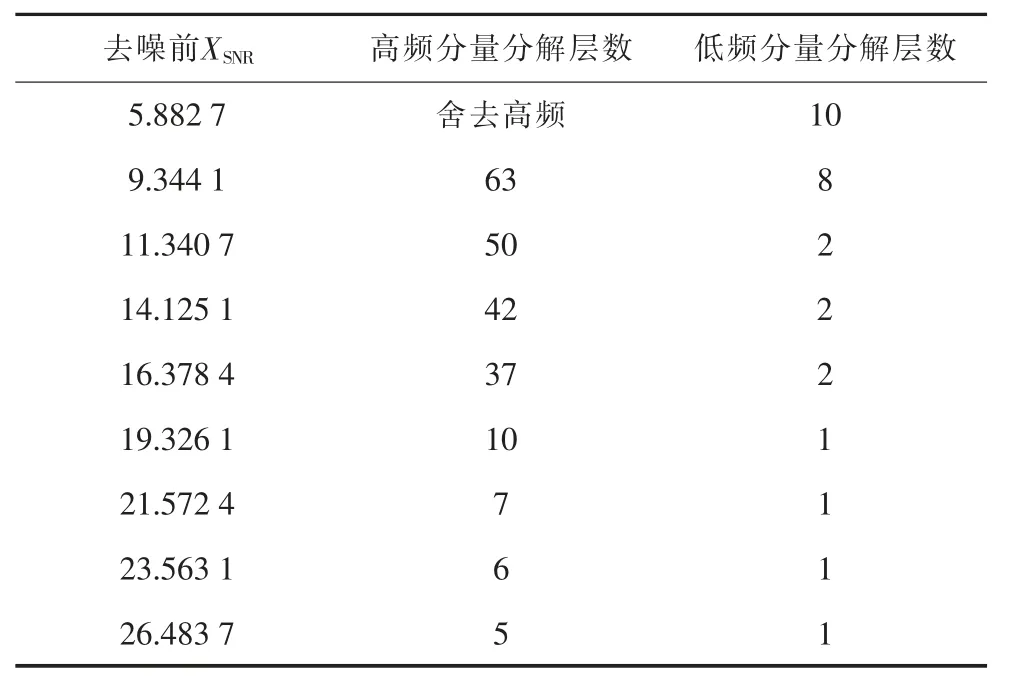
表4 不同噪声环境分解层数

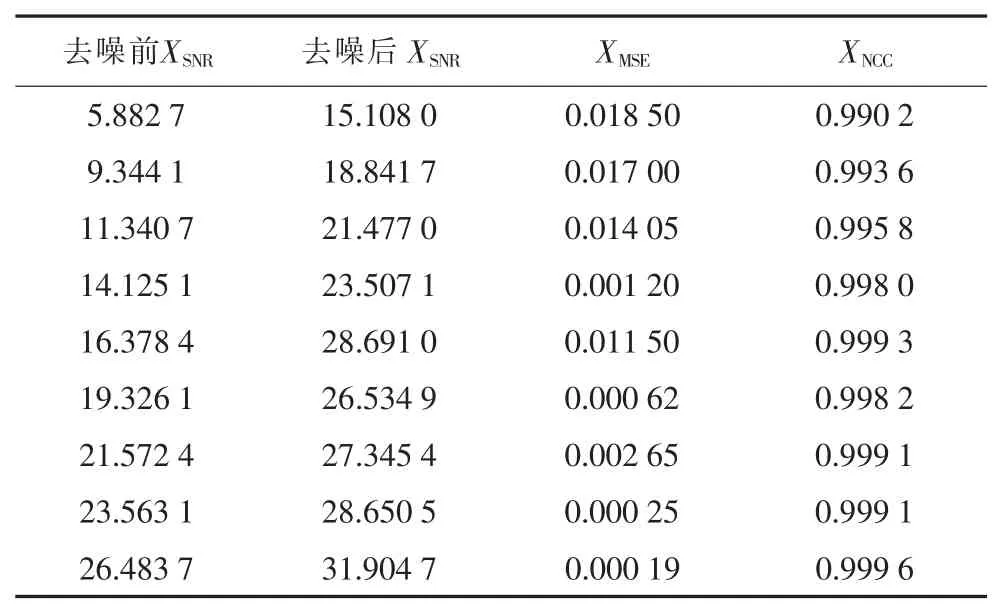
表5 不同噪声环境的去噪指标

3.2 Simulink 仿真

系统仿真结构如图7 所示。

通过分别模拟单相接地短路故障以及电动机投入，得到低压侧M 处的电压暂降波形，并在其中加入35 dB 噪声，然后利用本文方法进行去噪，结果分别如图8、图9 所示。

图7 系统仿真结构

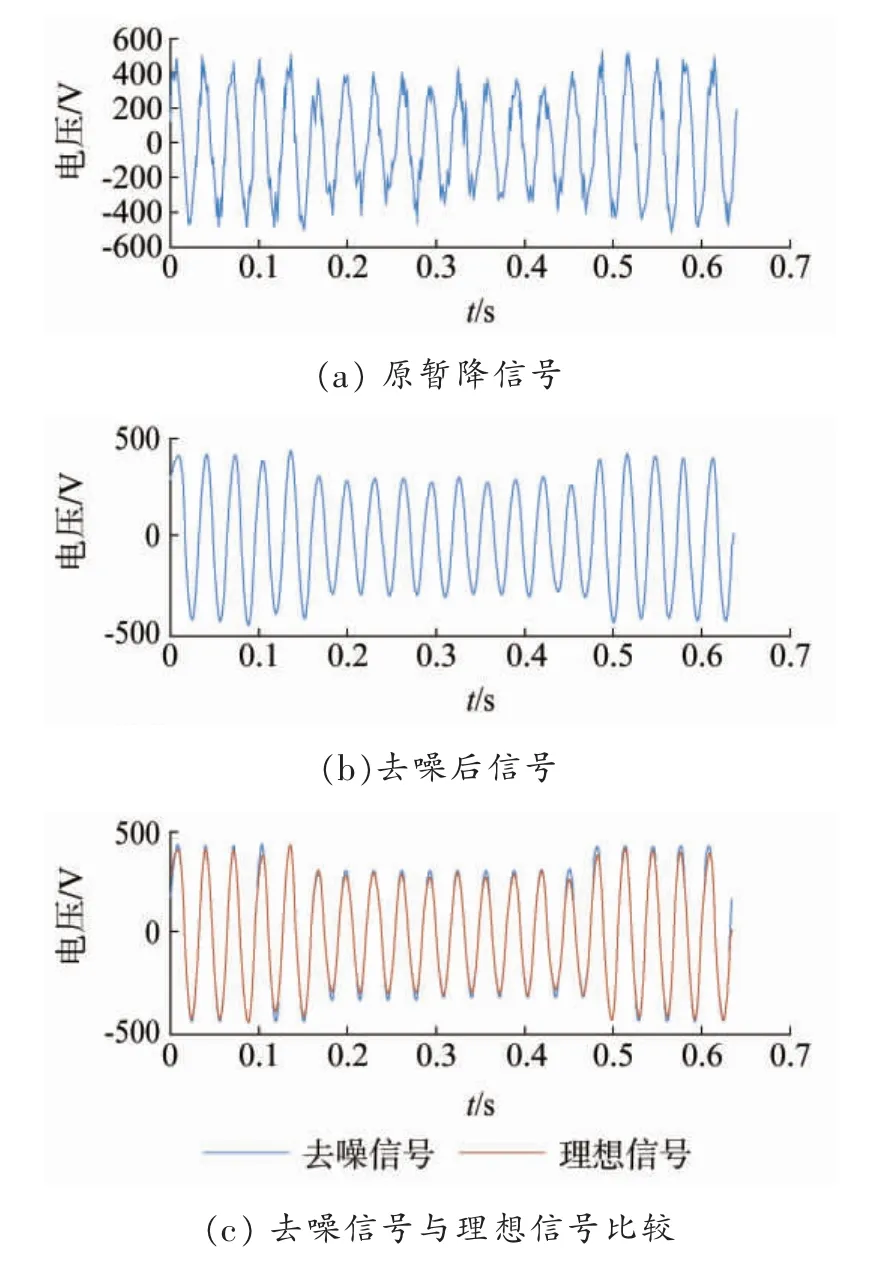
图8 单相接地短路电压暂降

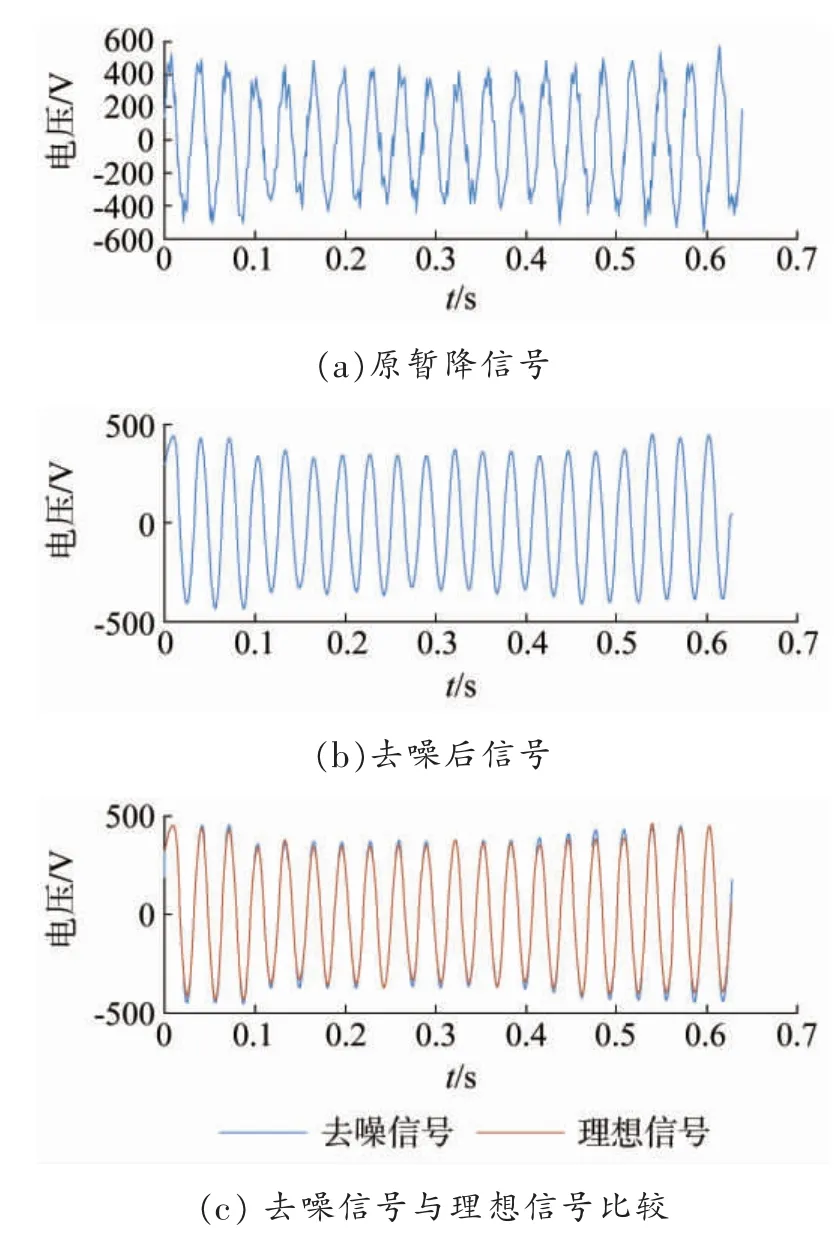
图9 电动机投入电压暂降

通过MATLAB 结果分析，本文去噪方法在不同信噪比条件下能显著提升XSNR，且重构后XMSE较小，XNCC均在0.99 以上。对于Simulink 电压暂降仿真信号，本文所述方法同样取得了较好的效果，去噪后无波形畸变，有效保留了暂降特征，再次证明了方法的可行性。

4 结语

提出一种EEMD 与自适应MRSVD 相结合的去噪新方法，并以含噪电压暂降信号为例进行仿真分析。一方面，显著提高的信噪比和极小的均方误差可定量地表明该方法去噪效果优良；另一方面，从波形相似系数和去噪后信号直观波形，定量与定性地验证该方法能很好地保留原始信号的特征信息。这对电能质量信号不失真去噪提供了新思路，也为电能质量信号检测及识别提供了有力保障。