分数阶忆阻带通滤波混沌电路动力学特性分析

马 晨 光， 于 晓 强， 杨 飞 飞， 牟 俊

( 大连工业大学 信息科学与工程学院, 辽宁 大连 116034 )

0 引 言

忆阻器是除电阻、电容、电感以外的第4种基本电气元件。由忆阻器构建的混沌电路可被广泛地应用于物理、生物医学、保密通信及信息安全领域[1]，因此构建性能良好的忆阻混沌电路引起了学者广泛关注[2]。忆阻器是描述电荷与磁通量之间关系的器件，一般分为荷控忆阻器和磁控忆阻器，其主要区别在于主导量的不同，荷控忆阻器的主导量是电荷，而磁控忆阻器的主导量是磁通量[3]。迄今为止，有许多基于忆阻器的混沌电路被提出。其中，牟俊等[4]利用常用的电子元件等效了有源忆阻电路，通过电路仿真证明了等效电路的有效性；阮静雅等[5]基于洛伦兹系统设计出了一个超混沌忆阻电路，并分析了其动力学特性；叶晓林等[6]基于文氏桥自激振荡电路设计出超混沌系统，利用SE和C0复杂度算法分析了系统的动力学特性。这些分析都是基于整数阶忆阻混沌电路，相比于整数阶忆阻混沌系统，分数阶忆阻混沌系统往往具有更为复杂的动力学特性。

分数阶微积分定义主要有Riemann-Liouville 分数阶微积分定义和Caputo分数阶微分定义。分数阶混沌系统求解方法主要有3种，分别是频域分析法[7]、预估校正法[8](ABM)和Adomian算法(ADM)[9]。其中ADM算法精度较高，收敛快，不需要离散化处理，并且占用的计算机内存较小，被广泛地应用于分数阶混沌系统的分析。孙克辉等[10]采用直接观测相图、计算功率谱等方法对分数阶统一混沌系统的动力学特性做了详细的分析；贺少波等[11]利用ADM算法对分数阶离散洛伦兹系统进行数值分析；Xu等[12]利用ADM算法对简化统一分数阶混沌系统进行动力学特性分析。这些研究表明分数阶混沌系统通常比整数阶混沌系统具有更复杂的动力学特性。Bao等[13]设计出一个简单的三阶忆阻混沌电路，并对其混沌特性进行了详细的分析，但是没有对分数阶系统进行分析。

因此，本文在三阶忆阻混沌电路基础上，设计了一个新的分数阶忆阻带通滤波混沌电路系统，利用SE和C0复杂度算法[14]评价系统的随机性，对其进行了详细动力学特性分析。

1 BPF忆阻混沌电路系统

一个改进的荷控忆阻等效电路如图1所示。该电路由1个电容、2个乘法器、3个电阻和2个运算放大器组成，其中v和i分别代表输入端的电压和电流，V0代表积分电容C0两端的电压，g是乘法器之间的比例系数。该忆阻器可表述为

(1)

图2(a)是带通滤波电路，与典型的文氏振荡电路类似，但拓扑结构并不相同。将图2(a)中的电阻R替换为图1所示的改进型荷控忆阻器，得到忆阻带通滤波混沌电路(图2(b))。

根据忆阻器模型和忆阻电路，基于基尔霍夫定律和欧姆定律，可得系统电路方程：

(2)

式中：k=1+R2/R3，V0，V1，V2为电路中3个结点的电位，令x=V0，y=V1，z=V2，u=du/dτ(u≡x，y，z)，C1=C2=C，τ=t/R1C，a=R1C/RbC0，b=R1C/RaC0，c=R1/Rc。代入式(2)对电路参数做无量纲处理，可得系统方程为

(3)

令a=8，b=80，c=500/3，g=0.1，k=21。

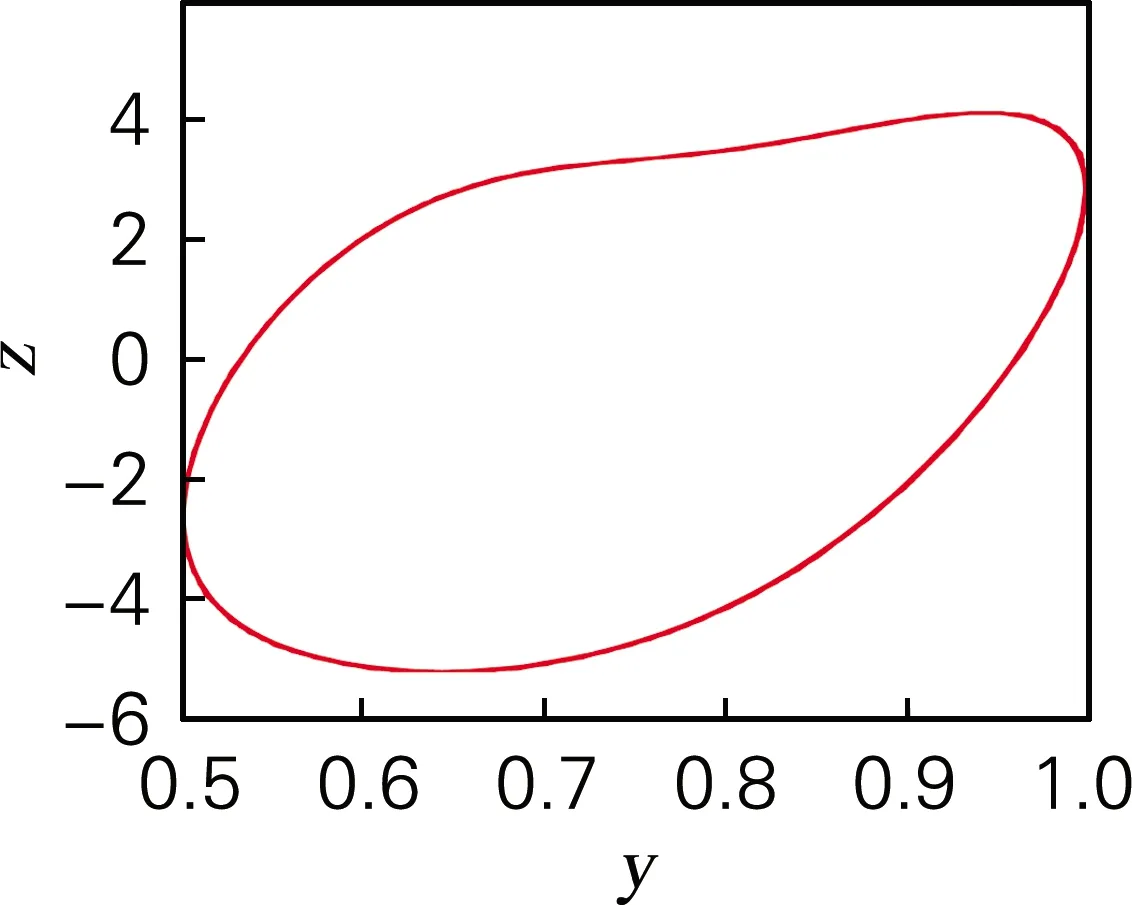
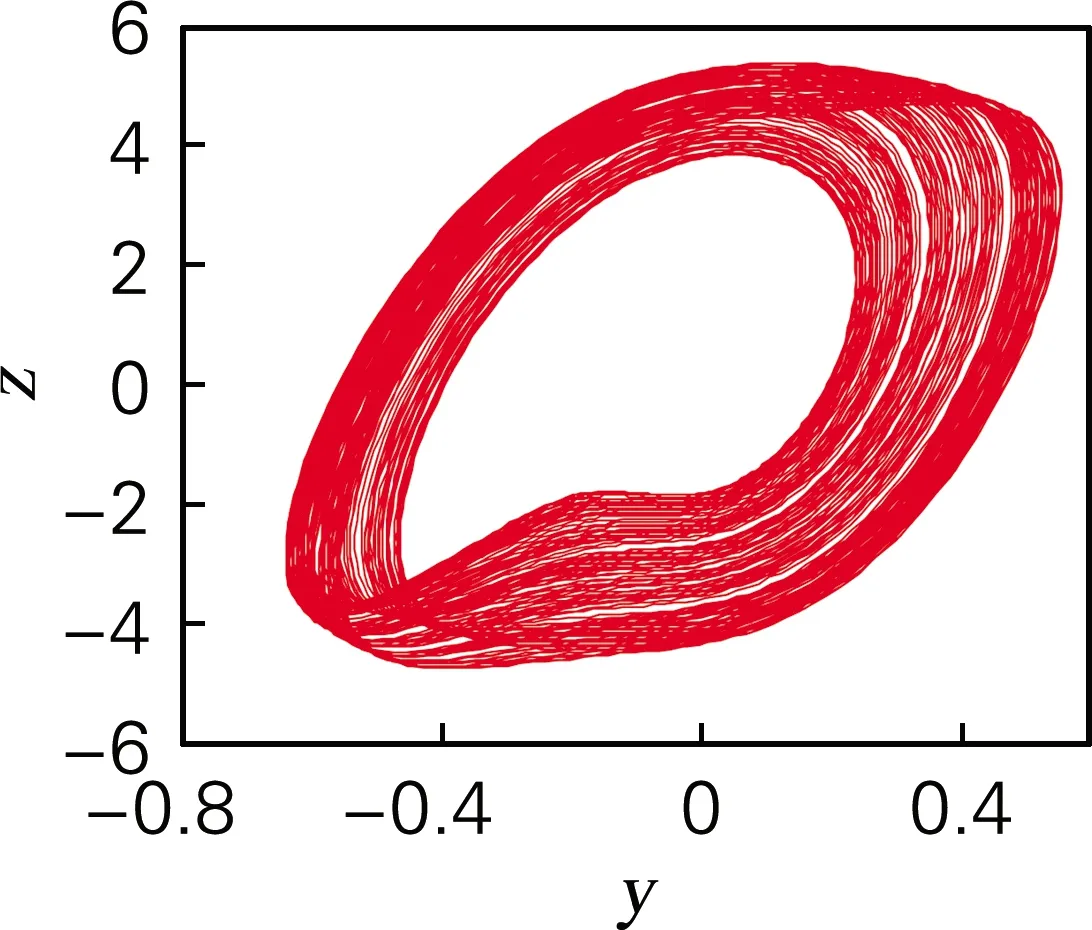
由于系统动力学方程不含常数项，显然(0，0，0)是系统(3)的平衡点。在平衡点附近任选取一点为初始值，观测该系统吸引子的范围，若初始值选取在吸引子范围之外，则系统发散。选取x0=[0，0.000 001，0]为初始值，此时吸引子相图如图3所示，系统的李雅谱诺夫指数为(1.089 3，0，-6.224 0)，李雅普诺夫分数维度DL=2.175。此时系统处于混沌状态。

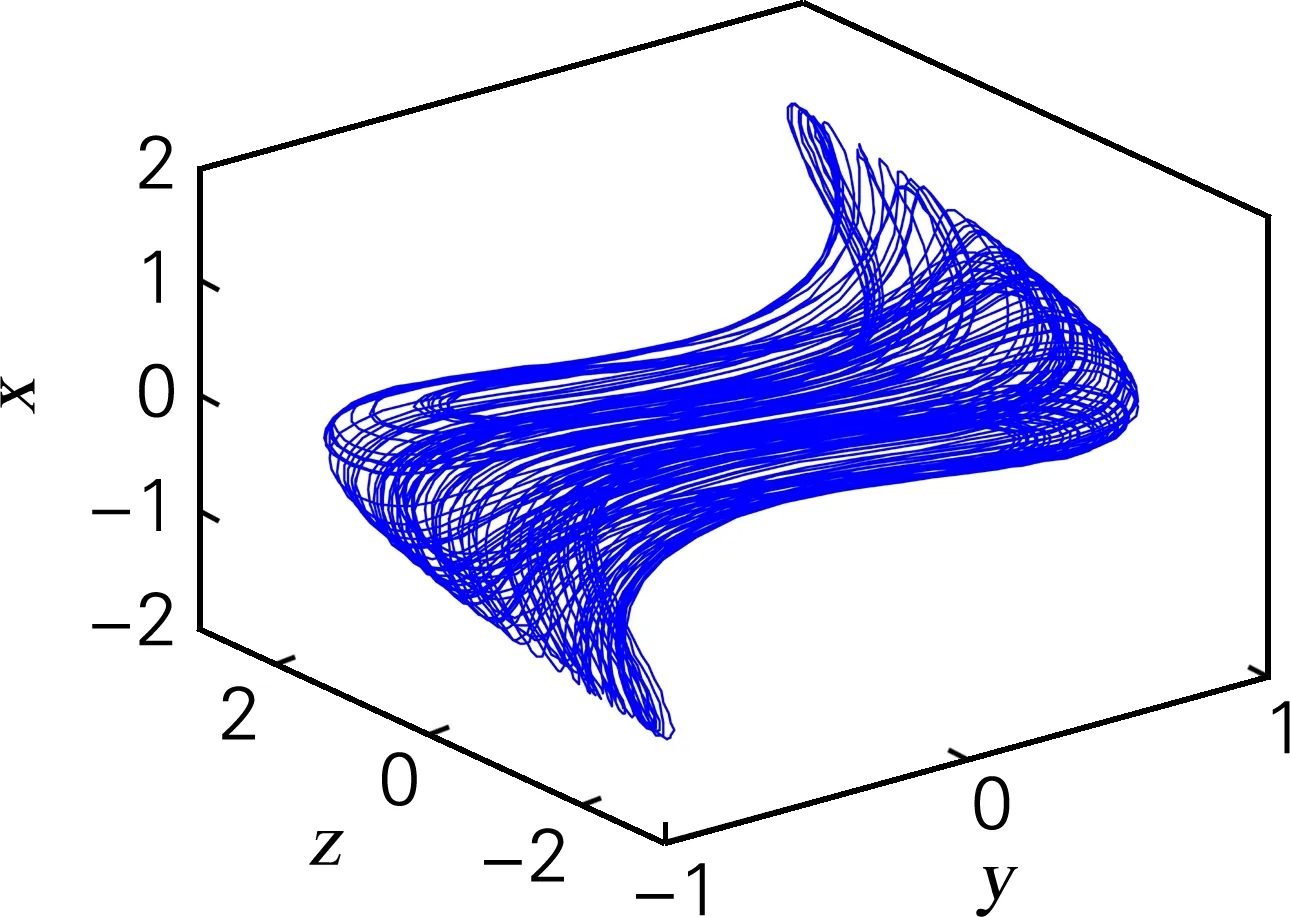
图3 三维吸引子相图Fig.3 Diagram of 3D attractor phase

2 分数阶忆阻混沌电路的数值分析

2.1 Adomian分解算法

(4)

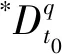
(5)

根据Adomian分解法原理，非线性部分可分解为

(6)

式中：i=0，1，…；j=0，1，…，n。由此非线性项可表示为

(7)

因此方程(4)的解为

(8)

其运算关系为

(9)

2.2 系统方程的数值解

由系统方程(3)，可得分数阶忆阻混沌电路的系统方程：

(10)

根据Adomian算法，系统线性、非线性和常数部分为

(11)

(12)

(13)

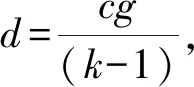
(14)

根据式(6)对非线性项x12x2进行分解，在保证计算精度的前提下截取前5项，可表示为

(15)

(16)

由初始条件可得

(17)

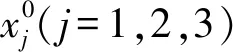
(18)

令

(19)

(20)

(21)

(22)

(23)

则系统方程的解为

(24)

在求解过程中将积分区间分成区段(tk，tk+1)，所得结果为区段(tk+1，tk+2)的初始值。令h=(tk-tk-1)，共需要(tk+1-tk)/(h-1)次迭代。

3 分数阶忆阻混沌电路动力学分析

3.1 参数a变化对系统动力学特性的影响

令q=0.9，初始值x0=[0，0.000 001，0]，h=0.001。此时系统相图(见图4)，系统的李雅谱诺夫指数为(1.825 5，0，-12.925 1)，李雅普谱夫分数维度DL=2.141 2。其中，只有一个正的李雅普诺夫指数，因此系统此时处于混沌状态，且此时最大李雅谱诺夫指数比整数阶最大李雅谱诺夫指数大，系统具有更为复杂的混沌特性。

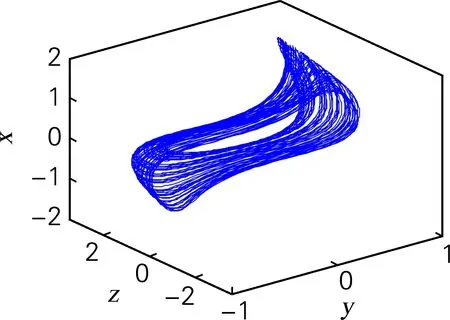
图4 a=8时的系统三维相图Fig.4 3D phase diagram of system with a=8

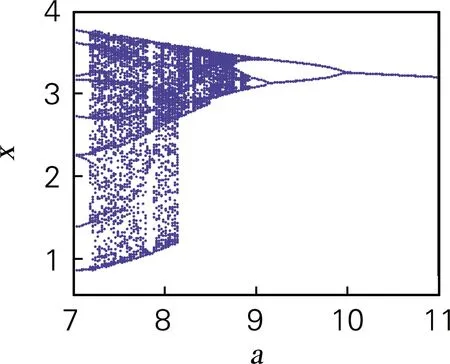
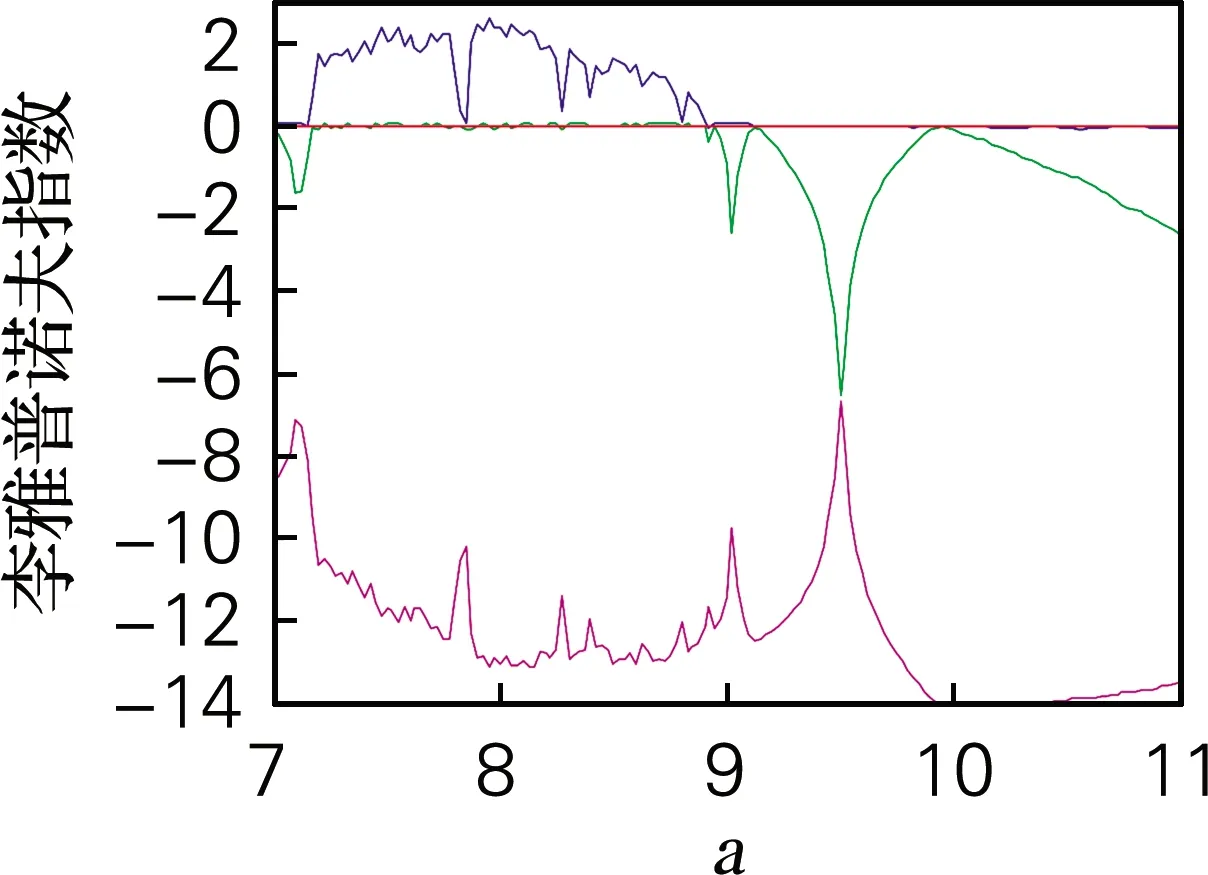
令q=0.9，当a从7变化到11时的系统的分岔图如图5(a)所示。当参数a∈(7，7.172)和a∈(8.925，11)时，系统处于周期态。而当a∈(7.172，8.925)时，系统处于混沌态。

(a) 分岔图

(b) 李雅谱诺夫指数谱

(c) SE复杂度

(d) C0复杂度

图5 系统复杂度随参数a变化

Fig.5 The influence of parameter a on the system

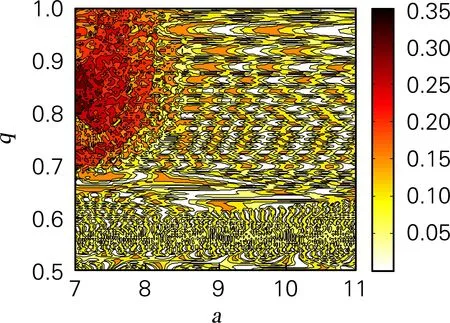
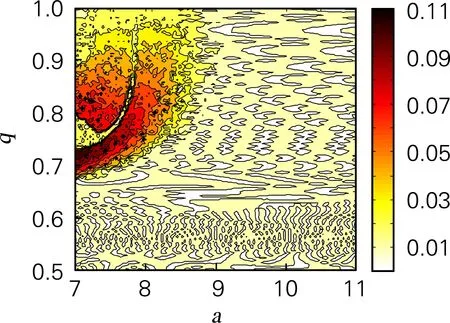
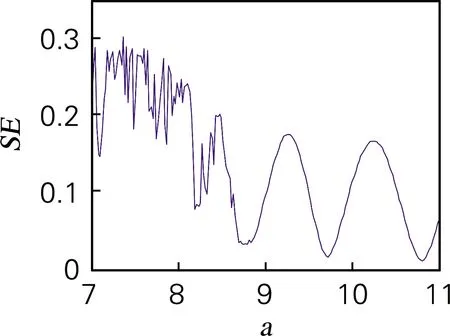
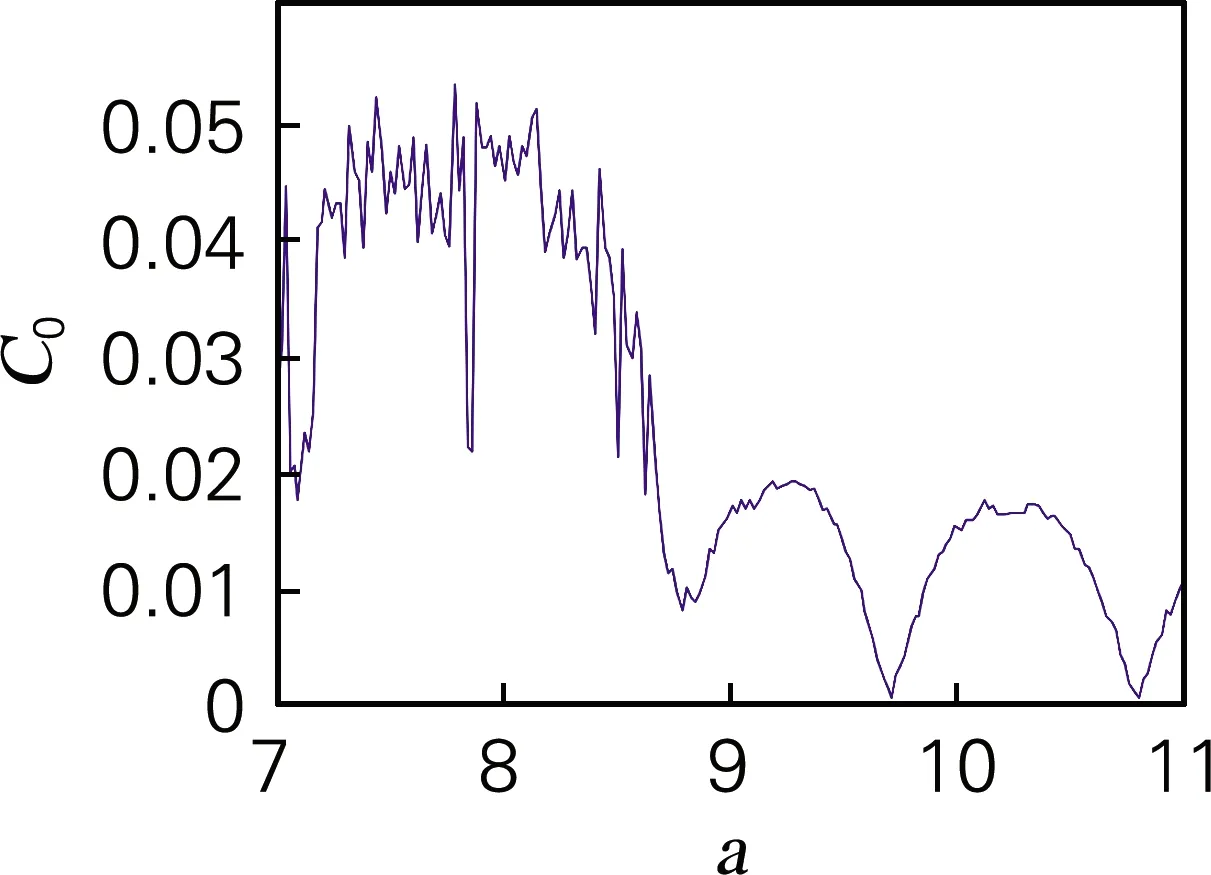
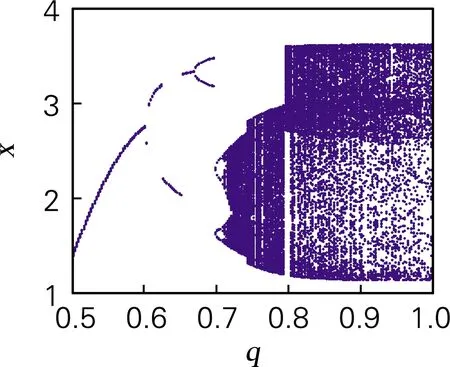
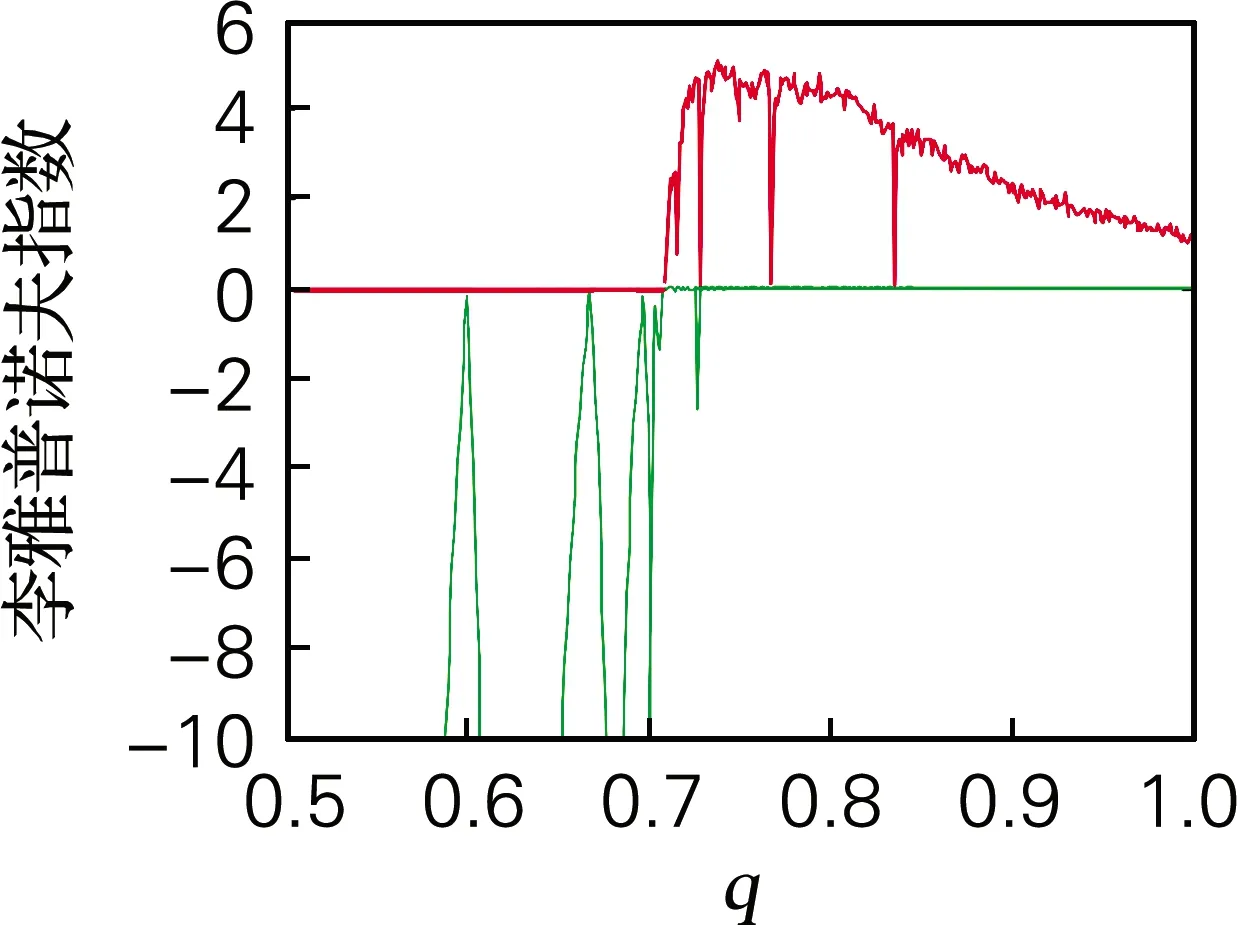
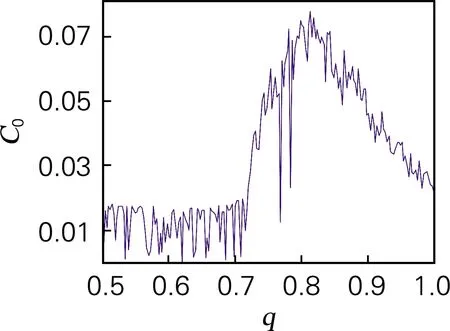
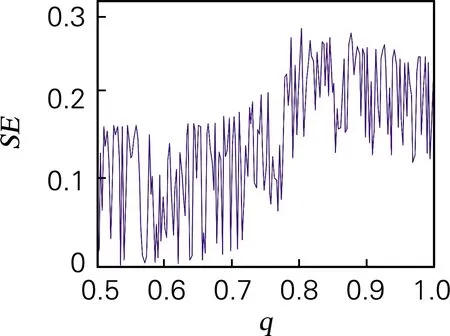
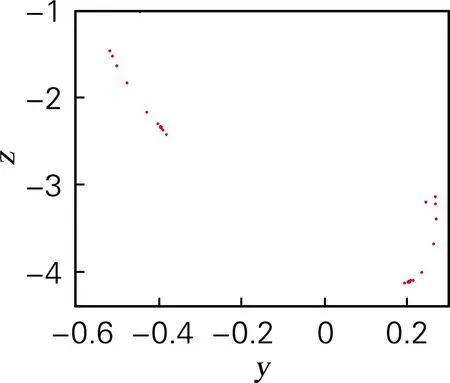
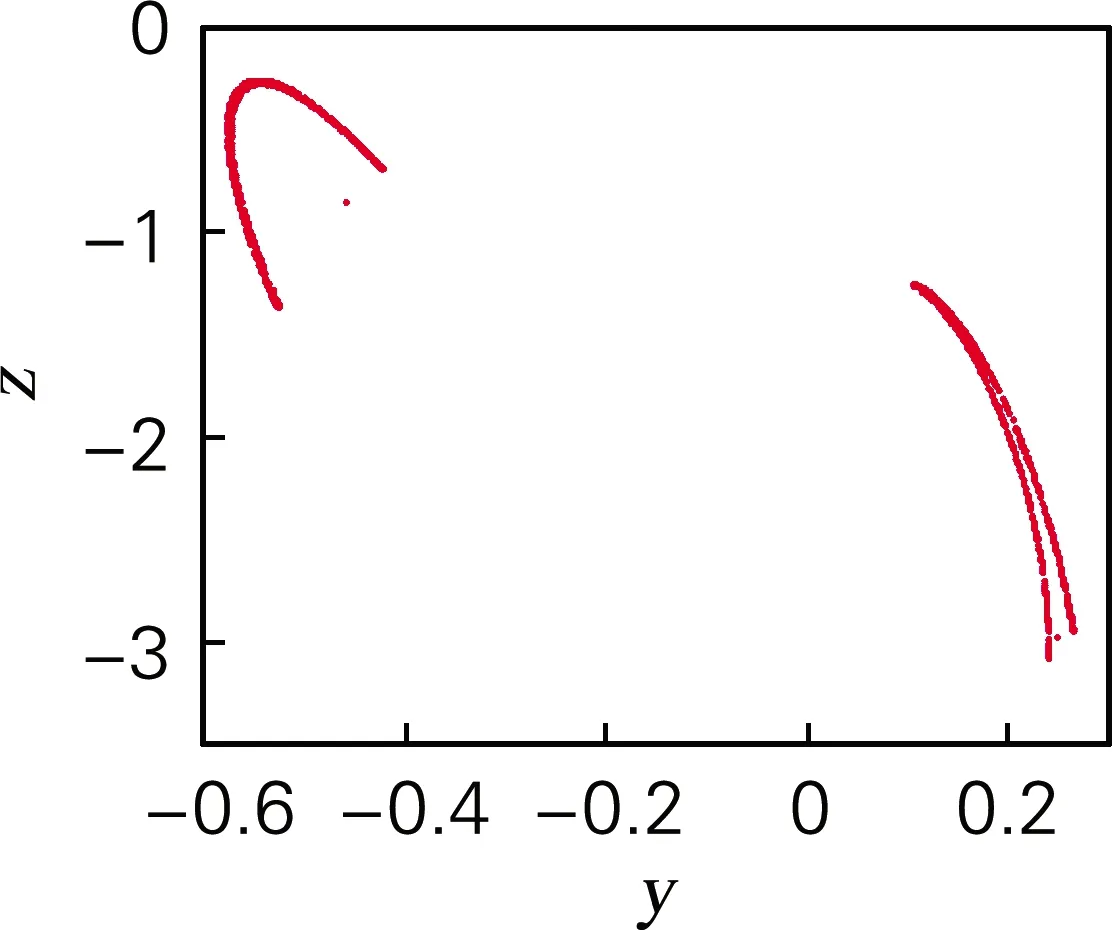
基于ADM算法，利用QR分解法求出系统随参数a变化的李雅谱诺夫指数谱如图5(b)所示。当a∈(7.172，8.925)时，系统的李雅谱诺夫指数为正值，系统处于混沌状态，这一结论与分岔图相对应。特别地，当7.809

3.2 系统随阶数q变化的动力学特性

令a=8，仿真结果表明，当q<0.4时，系统处于发散状态，q∈(0.4，0.709)时，系统是周期态。取q∈(0.5，1)，并保持其他参数和初始值不变时，系统的分岔图如图6(a)所示。当q>0.709时，系统通过倍周期分岔进入混沌状态。系统随阶数q变化的李雅谱诺夫指数谱如图6(b)所示，系统混沌特性主要被最大李雅普诺夫指数影响，因此为了显示清楚，图6(b)中省略最小李雅谱诺夫指数曲线。从李雅谱诺夫指数谱中同样可以看出李雅谱诺夫指数随阶数q的增加而增加，产生混沌的最小阶数为0.709，与分岔图完全对应。

为进一步分析系统的动力学特性，分析随阶数q变化时系统的C0和SE复杂度如图6(c)、图6(d)所示。当0.50.709时，系统进入混沌态系统的复杂度增大，其动力学特性更加复杂。

令a=8，q分别取0.65和0.8，初始值x0=[0，0.000 001，0]。作出系统在y-z平面的相图和在x=1平面，y-z轴的Poincaré截面如图7所示，当a=8，q=0.65时，系统相图为一个极限环，Poincaré为离散点；a=8，q=0.8时，系统出现混沌吸引子，Poincaré为分形结构的密集点，均与分岔图、李雅谱诺夫指数谱相对应。

3.3 系统随参数a和阶数q同时变化时的动力学特性

令初始值为x0=[0 0.000 001 0]，h=0.001，并保持其他参数值不变。基于谱熵SE和C0算法，得到二维SE和C0复杂度等高线如图8(a)、(b)所示。该图表示系统随参数a和阶数q同时变化时的复杂度，为选取合适的系统参数和阶数，以便对其进行更好的应用提供了参考。在图8中，不同的颜色代表了复杂度的不同，颜色越深代表复杂度越高，混沌序列随机性越高。SE复杂度的最大值为0.371 2，对应的a=7，q=0.824 3，最大李雅谱诺夫指数为3.419；C0复杂度的最大值为0.111 3，a=7，q=0.720 7，最大李雅谱诺夫指数为6.324 3。需要指出的是在当a=7，0.720 7

(a) 分岔图

(b) 李雅谱诺夫指数谱

(c) C0复杂度

(d) SE复杂度

图6 系统复杂度随阶数q变化

Fig.6 The influence of orderqon the system

(a) y-z平面(q=0.65)吸引子相图

(b) Poincaré截面(q=0.65)

(c) y-z平面(q=0.8)吸引子相图

(d) Poincaré截面(q=0.8)

图7 系统相图和Poincaré截面

Fig.7 Phase diagram and Poincaré section of the system

4 结 论

在构建的忆阻带通混沌滤波电路基础上基于Adomian算法计算了分数阶忆阻混沌电路的数值解。分析结果表明，分数阶忆阻混沌系统相比于对应的整数阶混沌系统，系统的李雅普诺夫指数更大。SE和C0分析表明系统的结构和序列更加复杂，更适合应用于保密通信领域。参数a=7，阶数q∈(0.8，0.9)时，系统混沌序列的随机性最好，安全性最高。研究结果为将忆阻带通滤波混沌电路应用于保密通信等领域提供了理论基础，具有较高的理论和应用价值。

(a) 二维-SE复杂度

(b) 二维-C0复杂度

图8 系统随参数a和q变化的复杂度

Fig.8 Complexity of the system varying with parametersaand orderq