关于函数压轴题的解题策略探讨与建议
周华


[摘 要] 函数压轴题的解题过程是知识调用、问题转化的过程,该过程中需要使用相应的解题技巧,其中数形结合是直观呈现问题、构建模型、严密推理的常用策略. 文章通过分析函数压轴题,思考数形解题策略,结合实例探讨函数压轴题的突破过程,提出相應的教学建议.
[关键词] 函数;策略;思想;数形结合
函数是初中数学的重点内容,也是知识综合性最强的内容之一. 纵观近几年的中考题,函数作为压轴题出现的频次很高,常联合平面几何、代数方程、不等式等内容来命制考题. 命题特征鲜明,常采用连续设问方式,难度逐问递增,各问之间具有一定的关联性和铺垫作用,能够引导学生思考,全面考查学生的知识水平和逻辑推理能力.
实际上函数是数形结合最为紧密的内容,函数解析式与图像之间存在着对应关系,从思想层面来看,是对数形结合思想的体现. 函数问题考查的知识内容十分丰富,在实际研究时需要全面考量函数图像,分析变量关系,总结结论. 基于数形结合思想建议采用如下解题策略:
1. 画图解信息,由图析关系(由形析数)
对于函数压轴题可利用图像来解析题干条件,提取隐含信息. 首先绘制图像,充分解读题干条件,利用图像的直观性来挖掘其中的几何特性.
2. 列式得未知,代数分析解(用数解形)
把握隐含信息,利用图像中的点来求解所涉函数关系式,通过解方程、不等式或函数分析的方式来获取关键量,逐步剖解问题.
考题探究
函数压轴题的综合性很强,其解法也不唯一,从不同的角度分析可以获得不同的信息条件,但均可以按照上述所推荐的数形策略来构建思路,下面以一道函数压轴题为例加以探讨.
问题:(函数与几何的综合)已知抛物线的解析式为y=ax- 2-2,其顶点为A,点B- ,2和C ,2是抛物线上的两个点,试回答下列问题.
(1)求该抛物线的解析式;
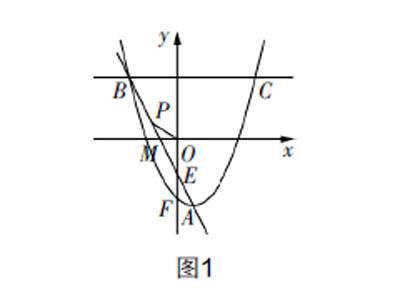
(2)如图1所示,过点A和B的直线与x轴和y轴的交点分别为点M和E,抛物线与y轴的交点为F,点P位于直线AB上,若有∠OPM=∠MAF,试求△POE的面积;
(3)如图2所示,点Q位于折线A-B-C上,过点Q作y轴平行线,再过点E作x轴的平行线,设两线交点为N,将△QNE沿着直线QE翻折,可得△QEN1,若点N1刚好落在x轴上,试求点Q的坐标.
思路突破:
第(1)问求抛物线的解析式,只需要将抛物线上已知坐标的一点代入解析式即可,将- ,2代入y=ax- 2-2中,可解得a=1,则该抛物线的解析式为y=x- 2-2.
第(2)问求所构三角形的面积,核心条件是等角关系“∠OPM=∠MAF”. 基于数形结合策略进行问题分析,根据条件信息理解图像,显然△POE由直线AB、OP和y轴合围所成. 点A坐标已知,点B、E、F、M的坐标均可以联立方程获得. 连接AF后,由“∠OPM=∠MAF”可知OP∥AF,后续需要分两步进行:第一步构建面积模型,第二步利用条件列方程求相关未知量. 有以下两种方法.
若将△POE视为以OE为底、点P为顶点的三角形,则其面积可以表示为S△POE= ·OE·h,其中h表示点P到y轴的距离,数值上与点P横坐标的绝对值相等. 将直线AB的解析式设为y=kx+b,分别代入点A和B的坐标,则可求得解析式为y=-2x-1,从而可得点E(0,-1),F0,- ,M- ,0. 由∠OPM=∠MAF可知OP∥AF,从而可证△OPE∽△FAE,由相似性质可得 = . 其中利用两点之间的距离公式可得OE=1,EF= ,AF= ,代入可解得OP= . 点P位于直线AB上,可将其坐标设为(t,-2t-1),从而可解得t1= - ,t2=- ,分析可知点P的两个位置均满足等角条件,将其分别代入面积模型可求得△POE的面积,当t1=- 时,可得S△POE= ;当t2=- 时,S△POE= ,所以△POE的面积为 或 .
第(3)问涉及几何折叠,同时点Q在折线A-B-C上运动,需要利用折叠特性进行分类讨论. 结合图像分析可知需要分为三种情形:①点Q在AB上运动,②点Q在BC上运动,且位于y轴的左侧;③点Q在BC上运动,且位于y轴的右侧. 具体分析时需要提取其中的基本图形,结合图形性质来构建方程求坐标.
①当点Q在AB上运动时,如图3所示,设点Q(a,-2a-1),则NE=-a,QN= -2a,根据翻折特性可得QN′=QN=-2a,N′E=NE=-a. 分析可知△QRN′~△N′SE,根据相似性质可得 = = ,代入可解得QR=2,结合NE+ES=NS=QR,可得-a+ =2,则a=- ,所以点Q的坐标为- , .
②当点Q在BC上运动,且位于y轴的左侧时,如图3所示. 设NE=-a,则N′E=-a,易得RN′=2,SN′=1,QN′=QN=3,则QR= ,SE= +a. 在Rt△SEN′中使用勾股定理可得SE2+SN′2=EN′2,解得a=- ,所以点Q的坐标为- ,2.
③当点Q在BC上运动,且位于y轴的右侧时,如图4所示,按照情形2的思路进行方程构建,设NE=a,则N′E=a,易得RN′=2,SN′=1,QN′=QN=3,则QR= ,SE= -a. 在Rt△SEN′中使用勾股定理可得SE2+SN′2=EN′2,解得a= ,所以点Q的坐标为 ,2.
综上可知,满足条件点Q的坐标有三个,分别为- , 、- ,2和 ,2.
上述是抛物线与平面几何相综合的压轴题,其中涉及几何角相等、求解三角形模型、图形翻折等几何内容,这也是函数综合题常见的命题方向. 上述采用了数形结合构建思路的策略,过程中体现了该策略解题的三个关键点:一是利用图像来理解题意,这是解题的前提;二是利用图像来转化条件,主要体现在后两问上,以第(2)问为例,结合图像将等角关系转化为三角形相似关系,以及直线斜率相等关系;三是利用图像模型来构建方程,无论是求直线解析式,还是求点坐标参数,均体现得淋漓尽致.
解后反思
函数与几何压轴题的突破需要完成图像分析与代数转化两个过程,上述呈现了数形结合解题的具体步骤,下面提出两点教学建议.
1. 重视观察,探析特性
函数与几何压轴题的特点是信息含量大,图像较为复杂,基于数形结合开展解题教学时需要使学生明晰信息理解的重要性,包括文字、符号和图像信息,在该阶段要完成题干条件与问题图像的对照转化. 因此需要引导学生重视观察图像,掌握读图技巧,例如提取曲线与坐标的交点、曲线之间的交点,关注其中的特殊图形,提取图形特性,以此为切入点来挖掘隐含条件,构建相应的思路. 考虑到图像较为复杂,具体教学时可以采用简图分析的方式,引导学生对复合图形进行拆解,构建模型,如上述第(3)问分类讨论时分别提取了动点图模型.
2. 直观猜想,严谨论证
函数压轴题所涉线条较多,结合了几何运动内容的问题更为复杂,部分几何元素的内容不完全确定,此时就需要引导学生发挥想象来做出猜想. 猜想时需要整合题干中的基本条件,综合考虑、合理猜想,例如上述结合条件可以想到点P的位置有两个,后续只需要加以论证即可. 在论证过程中需要充分运用函数与几何性质,构建相应的方程、不等式,通过求解获得准确的点坐标、取值范围等内容,从而剔除其中的错误猜想,得出正确的结论. 教学中教师要充分贯彻“先假设,后验证”的思路,培养学生的直观想象、严谨推理能力.

