基于“问题链”的数学课堂教学研究
张婷

[摘 要] 基于“问题链”的数学课堂教学是一种教与学相互统一的过程,以“问题链”为主线,启发思路,对建构知识体系、培养良好思维习惯和提升数学能力有着极其重要的作用. 文章结合案例,论述从自主探究、精析例题、拓展延伸三個方面精心设计“问题链”,培养学生的数学能力,为创设高效课堂谋求最大利益.
[关键词] 课堂教学;自主探究;问题链;数学思维;能力
教育家陶行知曾说,“发明千千万,起点是一问”. 由此可见提问在教学中的重要意义. 对于教学而言,问题导学有着广泛的应用性,问题是教学的主要方式之一,对课堂教学的好坏有着直接的影响. 相较于其他学科,数学与问题有着浑然天成的适配性,恰到好处的问题可以激起学生的学习兴趣,培养学生的思维能力,启迪学生的创新灵感[1] . “问题链”是教师基于教学目标和具体学情,有针对地设计的层层递进、层次分明、相互关联的一系列数学问题,它是教师穷追不舍的连续提问,是帮助学生真正破解问题本质的载体,也是课堂有效提问的一种重要形式.
问题的提出
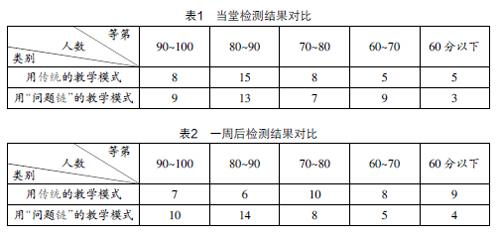
笔者选取了本人执教的两个初三平行班为实践对象,其中一个班采用传统教学模式,另一个班则接受“问题链”的教学模式. 本研究的因变量是学习者的“接受程度检测结果比对”. 在授课过程中,笔者明显感觉到了后者的课堂气氛活跃度远远胜于前者. 同时,笔者在授课完成后及时进行了一次当堂检测,检测结果对比如表1.
观察结果不难看出,传统教学模式的效果似乎优于“问题链”教学模式. 于是,在一个星期过后笔者又一次进行了一次关于这一节课的检测,检测结果比对如表2.
这一结果显示,“问题链”教学模式让70~80,80~90,90~100这三个阶段的学生人数奇迹般增加了,这一反差的出现让笔者甚感欣慰. 采用传统教学模式进行教学后,学生机械识记、模仿练习,事实上还并未完全理解,只能通过反复训练这种“高能耗,低效率”的方法进行巩固;而接受“问题链”教学模式的学生,理解和识记都较为牢固,教学效果也是显而易见的. 下面,笔者选取一个例题,设计基于“问题链”的数学探究教学基本流程.
设计方法与案例分析
1. 自主探究
问题1:一大型商场大量促销一批品牌T恤,平均每日可以售出T恤20件,且每件T恤售价60元,试求出一日的销售额.
分析:销售额=每件售价×销售量. 这一问题易于解决,每个学生都可以准确而快速地得出结论,课堂气氛异常活跃.
问题2:一大型商场大量促销一批品牌T恤,平均每日可以售出T恤20件,每件T恤售价60元,且每件T恤成本20元,试求出一日的销售利润.
分析:利润=(每件售价-每件成本)×销售量. 这一问题难度不算大,大部分学生都能较快解决,学生自然信心十足.
设计意图 教师从学生出发,将本节课的问题进行剖析,以“问题串”为载体进行呈现,激发学生的探究意识和发散思维. 在以上问题的解决中,一方面充分激趣和建立信心,启发学生高效精准地入课;另一方面揭示了销售利润和销售额这两个概念本质,促进了学生的深度理解.
2. 精析例题
问题3:一大型商场大量促销一批品牌T恤,平均每日可以售出T恤20件,每件T恤售价60元,每件T恤成本20元,为了增强盈利力度,商场进一步采取降价措施来扩大销售. 经过多番调查发现,T恤的单价每降低1元,该商场每日可多销售2件. 那么T恤的单价应降多少元,才能实现每日盈利1200元?
分析:这一问题由于涉及多个数量关系,学生理解起来有些困难. 笔者引领学生进行分析:若设T恤单价降x元,那么该商场平均每日可多出售T恤2x件,进一步利用等量关系“出售件数×每件盈利=1200元”可列方程求解. 同时,笔者再以列表的形式帮助学生明晰其中的多个数量关系(如表3).
问题4:如若在问题3的基础上再增设一条件“商场为了减轻库存积压”,那么答案又是什么呢?
分析:这一问题的抛出,引发了学生火热的讨论. 教师在巡视过程中,发现大部分学生认为问题4与问题3的答案并无不同,也有一小部分学生认为两个问题之间肯定存在着差异,看来思维困惑已然形成,此时加以干预可以为学生提供正确的思维方向. 笔者提示:“商家如何才能减少库存积压呢?”学生自然而然地给出答案:“卖得越多库存积压越少. ”笔者拾级而上,道:“如何才能卖得多呢?”此时学生顺势而下,自然得出需选择价格降得多的,从而使问题迎刃而解. 这里,教师以精准问题干预驱动了学生的准确思维.
问题5:如若在问题3的基础上再增设一条件“商场每日需支付水电等各种费用50元”,那么又该如何完成呢?
分析:这一问题的提出在这里应该是较易解决的,不过不少学生在实际解题中容易忽略,如若加以提醒自然毫无问题,具体公式为“出售件数×每件盈利-各项费用=1200元”.
问题6:如若将问题3中的“T恤单价每降低1元”变为“T恤单价每降低0.5元”,那么又该如何解决呢?
分析:这一问题的解决有一些难度,学生极易形成思维卡壳,不过只需牢牢把握“出售件数×每件盈利=1200元”这一等量关系,并找寻到出售T恤的件数,解决起来还是较为容易的. 这里可以设T恤单价降x元,那么这里降了 个0.5元,降一个0.5元即可多卖2件,则可以多卖 ×2件,从而得出每日可卖出20+ ×2件,再代入等量关系即可成功解决.
设计意图 在问题的解决过程中,针对学生思维困惑的现象,笔者及时施与援手并加以干预,巧妙抓住学生的“犹豫”和“争辩”,适时进行追问,有效且精准地将学生的思维引入问题的难点,极好地定位了自身的角色,同时将学生的思维引向纵深.
3. 拓展延伸
问题7:若商场想要每日获取最大利润,那么T恤的单价应降多少元?
分析:这一问题涉及求二次三项式的最值问题,自然是本节课的难点. 当然,这一问题在运用配方法解一元二次方程时已作要求,为了解决学生的思维困境,笔者提出问题:“如何求商场一天的利润?”学生很快给出了答案,从而使问题的解决水到渠成.
设计意图 通过“问题链”将学生的思维引向更高的层次,关注到思维过程的生成性,同时将知识的获取与能力的培养有机结合. 一个又一个问题的提出、探究和解决,让教学过程不是停留在知识传授的层面上,而是通过“问题链”的指引,让学生获取知识技能,培养学生的问题意识和思维能力.
结束语
本节课以“问题链”为教学的重要载体,通过7个题目进行推进,以一个简单问题导入,展开了探究式课堂的第一问,为学生的探究性学习供给了有效的抓手. 一个又一个问题的抛出有着较高的立意,既是上一个问题的深化,又向着高层次进行过渡,环环相扣,承上启下. 同时,随着提问的不断深入,学生自主探究的欲望越发强烈,问题意识逐步形成,有效提高了学生学习数学的积极性,更好地培养了学生的探究能力和创新意识[2] .
总之,“问题链”的设计关系到教学的目标和方法,决定着学生思维的深度和广度,影响着课堂教学的效果. 因此,我们有理由相信,基于“问题链”的数学课堂教学模式的广泛使用必将使课堂教学效果更上一个台阶,为创设高效数学课堂谋求最大利益 [3].
参考文献:
[1]张奠宙,张荫南. 新概念:用问题驱动的数学教学[J]. 高等数学研究,2004(05).
[2]赵玉玲. “问题链”教学法的探索与实践[J]. 现代教育,2012(Z1).
[3]管明贵. 精心设计问题串,提高课堂教学效益[J]. 数学大世界(中旬),2017(04).

