考虑冻融和应力影响的混凝土构件碳化试验研究

孙晓红，胡大琳，张雷雷，陈 峰，查 斌

(1.长安大学公路学院，西安 710064；2.苏交科集团股份有限公司，苏州 215000；3.在役长大桥梁安全与健康国家重点实验室，南京 211112)

0 引 言

混凝土的材料性能与环境作用息息相关，桥梁结构常年处于自然环境之中，混凝土易受到侵蚀，耐久性不足，而近年来的超重荷载，使得混凝土桥梁病害逐渐显现出来[1]。研究混凝土材料耐久性，对提高混凝土桥梁寿命，改善混凝土桥梁服务水平具有重要意义。

寒冷地区的混凝土结构经受不断的冻融与离子的侵蚀导致损伤，其并不只是简单的叠加问题，而是各因素互相影响的结果。据调查，冻融循环和碳化是影响我国北方地区混凝土结构耐久性的重要因素[2]。目前，单因素作用下混凝土结构侵蚀理论基本成熟，越来越多的学者已开始研究多因素耦合下的混凝土结构侵蚀规律[3]。在国内，Sun等[4]研究混凝土在荷载和冻融循环共同作用下的损伤及不同强度等级混凝土的反应。肖前慧[5]通过模拟冻融和碳化耦合的环境，对混凝土耐久性、动弹性模量变化及其碳化深度进行了试验研究。于琦[6]采用数值分析方法模拟混凝土冻融-碳化过程，并建立碳化深度预测模型。邓会江等[7]交替将混凝土试件置于冻融-碳化各2 h的环境中，与只进行冻融循环的混凝土进行对比，得知碳化可一定程度上提高混凝土的抗冻性。张鹏等[8]测定加入粉煤灰的混凝土在冻融碳化交替作用下的碳化深度。

本文设计不同应力条件下混凝土梁的纯碳化试验和冻融-碳化交替试验，为了进一步验证试验结果，用COMSOL Multiphysics(简称COMSOL)软件建立考虑冻融和弯压应力的钢筋混凝土试件碳化深度模型。

1 实 验

1.1 材料与试件

以桥梁工程中常用的C40混凝土为研究对象。为满足试验要求，制作边长为15 cm的混凝土立方体试块、尺寸10 cm×15 cm×75 cm的钢筋混凝土短梁试件以及尺寸10 cm×15 cm×150 cm的长梁试件，混凝土配合比如表1所示。长梁与短梁中，均在上缘与下缘布置牌号为HPB235的钢筋，试件钢筋布置如如图1所示。混凝土浇筑入模具成型后，在(20±5) ℃ 的环境中静置24 h后，拆模放置在温度(20±2) ℃，湿度95%以上的环境下养护至28 d龄期。对养生28 d龄期的混凝土立方体试块进行抗压强度测试。

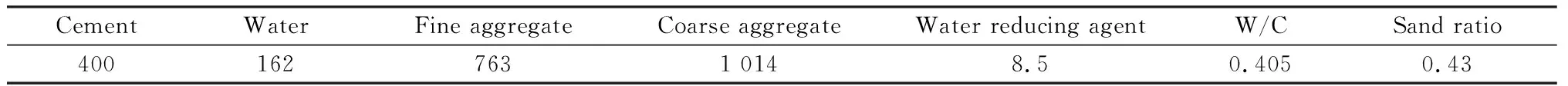
表1 混凝土配合比Table 1 Mixture proportion of concrete /(kg·m-3)

1.2 试验过程

试验分为纯碳化试验与冻融-碳化耦合试验两种，试验采用DQH-ZY-100D多功能气候模拟实验室进行。对纯碳化试验，将养生龄期28 d的两种钢筋混凝土梁放置在气候模拟试验室进行试验，试验条件为：温度(20±2) ℃，CO2浓度为(20±3)%。每个钢筋混凝土试件之间保持一定的间距，试件各表面同时处于碳化，分别在碳化7 d、14 d、21 d及28 d的时间节点取出相应的混凝土试件测量其碳化深度。

冻融-碳化耦合试验中，钢筋混凝土试件的碳化与冻融试验交替进行。试验分为四个阶段，当试件碳化7 d、14 d、21 d及28 d之后分别对应进行13次、12次、13次和12次的冻融循环试验。冻融试验采用气冻的方式，同样也使得试件处于多个面同时受冻的状态。在冻融前将试件在水中浸泡充分，使其达到完全水饱和的状态。冻融试验设置最低温度为-20 ℃，一次冻融循环约12 h，共分为3个阶段：(1)降温阶段：水饱和的试件在4 h内从室温降至最低温；(2)保温阶段：试件在-20 ℃ 的环境中保持4 h；(3)升温阶段：试件在20 ℃左右的水中解冻约4 h恢复至室温。冻融-碳化耦合试验中，作为对照，在与纯碳化试验相同的时间节点(7 d、14 d、21 d、28 d)对混凝土试件进行碳化深度的测量。

1.3 试件施加应力状态

为了研究钢筋混凝土构件应力状态对其碳化深度的影响，对钢筋混凝土短梁施加轴压与弯压的初始应力状态,对长梁施加纯弯的初始应力状态，维持应力状态进行冻融-碳化耦合试验；同时，作为对照组，对施加轴压应力的短梁试件进行纯碳化试验。试件试验方式如表2所示，其中编号“C”代表“碳化(Carbonation)”，其后的数字代表天数；编号“FT”代表“冻融循环(Freeze-Thaw Cycles)”，其后的数字代表循环次数;fck为C40混凝土抗压强度标准值;ftk为C40混凝土抗拉强度标准值，下文同。

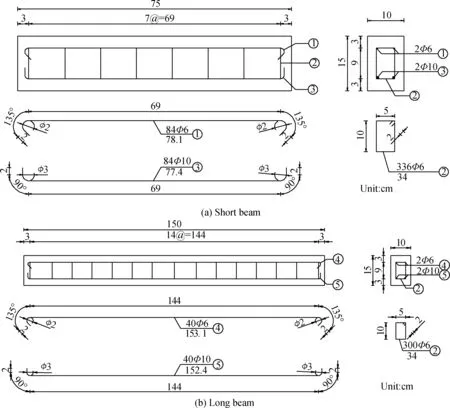
图1 钢筋混凝土试件钢筋布置图Fig.1 Layout of the reinforcement of beams

表2 试件初始应力状态及冻融-碳化试验Table 2 Initial stress state of specimens in the coupling tests of freeze-thaw-carbonation

应力加载使用混凝土构件耐久性试验持荷装置[9]完成，该装置主要由纵向轴力拉杆、横向弯矩拉杆、刚垫板、螺帽等配合千斤顶和压力传感器施加预定压力，具体操作按照装置说明的方法进行。短梁轴压、短梁弯压及长梁纯弯的三种应力状态的加载示意图及实际加载图分别如图2～图4所示。

1.4 碳化深度测量

在每个碳化深度测试节点7 d、14 d、21 d、28 d时，利用反力支架与千斤顶对梁试件的预加应力进行卸载。凿去试件中部上表面的表层混凝土，使用吹风机清除表面粉末，并喷洒浓度为1%的酚酞溶液。取试件破损处等间距的五个点的碳化深度的平均值作为该点的碳化深度值。测试图如图5所示。

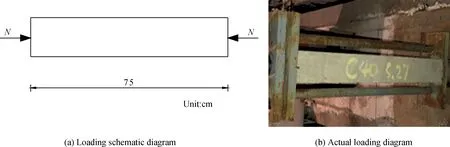
图2 短梁轴压应力状态Fig.2 Stress state of short beams under axial compression

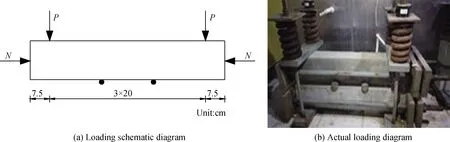
图3 短梁弯压应力状态Fig.3 Stress state of short beams under bending stress and axial compression

图4 长梁纯弯应力状态Fig.4 Stress state of long beams under bending stress

图5 试件碳化深度测量Fig.5 Measurement of carbonation depth of specimen

2 结果与讨论

2.1 混凝土碳化规律

2.1.1 冻融及轴压应力共同作用下对混凝土碳化的影响

根据轴压试件碳化深度测试结果，如图6所示，绘制纯碳化试验和冻融-碳化耦合试验下，不同轴压应力水平下试件碳化深度与时间的关系曲线。可以看出，无论在纯碳化或冻融-碳化耦合条件下，混凝土的碳化深度随时间均呈对数增长，随着时间的推移碳化深度增长速率逐渐减小。此外，在相同的碳化时间内，当轴向压力越大时，混凝土的碳化深度越小。这是因为压应力会减小混凝土内部孔隙率，导致CO2在其中的渗透速率减小，进而降低了碳化速率。说明压应力在一定程度上可以抑制混凝土碳化的发展。

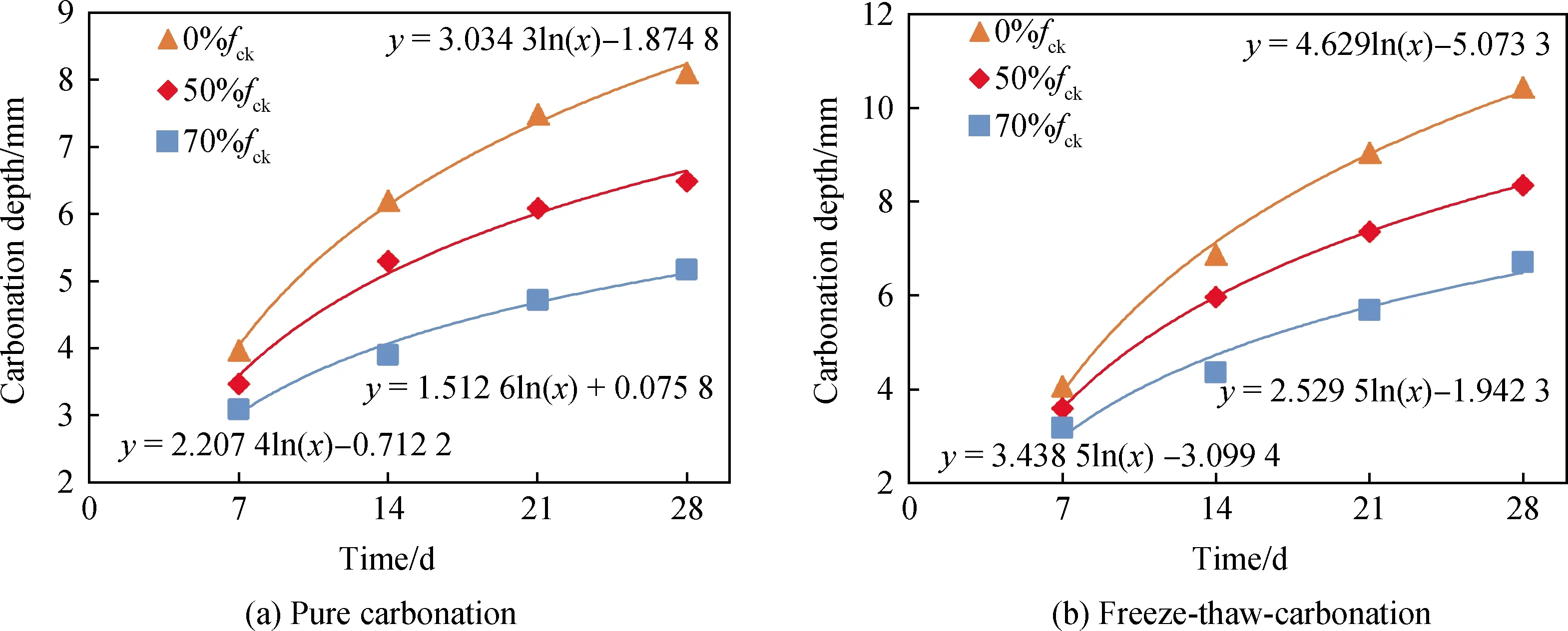
图6 轴压短梁试件的碳化深度曲线Fig.6 Curves of carbonation depth of axially compressed short beam specimens

为分析冻融循环对混凝土中性化的影响，引入碳化深度增长率ηi，由式(1)计算。

ηi=(Xi,C+FT-Xi,C)/Xi,C

(1)

其中，Xi,C+FT为冻融-碳化共同作用id时的混凝土碳化深度，Xi,C为纯碳化id时的混凝土碳化深度。ηi随时间变化的曲线如图7所示，由试验结果发现，混凝土的碳化深度增长率随着冻融-碳化的时间发展几乎呈线性增长，由此可见，在同一段时间内，冻融对碳化的促进作用是均匀增加的。此外，冻融循环对碳化的促进作用受混凝土试件的轴压应力水平的影响较小。

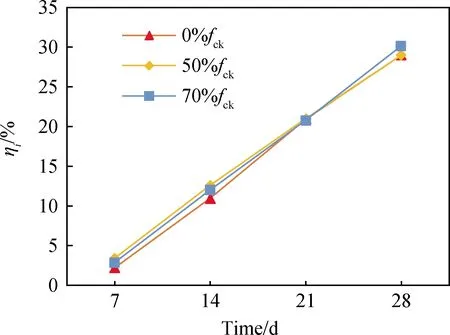
图7 冻融对不同轴压应力水平下ηi的影响Fig.7 Effect of freeze-thaw on the ηi under different axialcompression stress

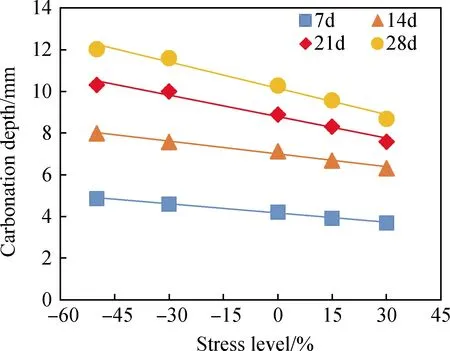
图8 不同弯曲应力水平下冻融-碳化对碳化深度的影响Fig.8 Effect of freeze-thaw-carbonation on the carbonationdepth under different bending stress

2.1.2 弯曲应力对冻融-碳化条件下碳化深度的影响

分析混凝土弯压和纯弯的冻融-碳化试验测得的碳化深度数值，如图8所示，绘制混凝土碳化深度与应力水平的关系曲线。其中以混凝土内部的压应力为正。结果发现，与无应力状态下的碳化深度相比，当混凝土内部存在拉应力时，混凝土碳化更加迅速，且碳化速率随着拉应力的增大而增大。这是因为拉应力会增大混凝土内部孔隙率，使得CO2在其中的渗透速率增大，导致碳化深度的增加。此外，从图中可以看出，在相同的碳化龄期内，碳化深度随应力的增加呈正比减小。由此推断，可以通过控制应力水平的方式来影响CO2在混凝土内部的渗透速率，进而控制混凝土的碳化速率以达到对混凝土结构的碳化防护。

2.2 碳化影响因素分析

为分析冻融循环、初始应力状态及其组合效应对混凝土碳化的影响，引入混凝土碳化程度系数λm，可利用式(2)计算。

λm=Xm+n/Xn

(2)

其中，m代表试验组混凝土碳化的影响因素，n代表对照组试验，Xm+n代表试验组混凝土碳化深度，Xn代表对照组混凝土碳化深度。若λm<1，则说明该影响因素对碳化起到抑制作用，值越小抑制作用越强；若λm>1，则说明该影响因素对碳化起到促进作用，值越大则促进作用越强。

2.2.1 冻融循环对碳化的影响

为分析冻融循环对混凝土碳化的影响，计算短梁试件在轴压应力为0%fck条件下分别经过纯碳化与冻融-碳化试验的碳化值。

引入冻融作用下碳化程度系数λFT，可按照式(3)计算。

λFT=XC+FT/XC

(3)

其中,XC+FT为冻融-碳化耦合试验中混凝土试件的碳化深度，XC为纯碳化试验中试件的碳化深度。计算结果如表3所示。λFT始终大于1，且随碳化的时间持续增长，说明冻融循环促进了混凝土的碳化，且促进效果逐渐增强。

表3 冻融循环对碳化程度系数λFT的影响Table 3 Effect of freeze-thaw cycles on the coefficient of combination degree λFT

2.2.2 轴压应力对碳化的影响

为分析轴压应力对混凝土碳化的影响，计算短梁试件在纯碳化作用下所受压应力分别为0%fck、50%fck与70%fck的碳化值。

引入不同压应力状态下碳化程度系数λP，可由式(4)计算。

λP=XP/X0

(4)

其中，XP为在纯碳化试验中50%fck与70%fck轴压应力状态下混凝土的碳化深度，X0为纯碳化试验中无轴压状态混凝土的碳化深度。计算结果如表4所示。结果发现，当混凝土试件施加压应力后，混凝土碳化程度系数λP<1，说明混凝土内部的压应力抑制了碳化的发展。此外，随着混凝土内部的压应力从50%fck升至70%fck时，λP的值减小，说明压应力的增加有助于减缓碳化的发展。

表4 轴压应力对碳化程度系数λP的影响Table 4 Effect of axial compressive stress on the coefficient of combination degree λP

2.2.3 冻融-应力共同作用对碳化的影响

为分析冻融-应力共同作用对混凝土碳化的影响，计算试件处于应力状态分别为轴压50%fck及70%fck、弯压30%fck及15%fck与纯弯30%ftk及50%ftk下，经过冻融-碳化后的碳化值。

引入冻融-应力共同作用下碳化程度系数λFT+P，可由式(5)计算。

λFT+P=XFT+P/X0

(5)

其中，XFT+P为在冻融-应力耦合作用下混凝土的碳化深度，X0为纯碳化试验中无轴压状态混凝土的碳化深度。计算结果如表5所示。本试验设置的4组不同压应力水平，在与冻融循环耦合后对混凝土的碳化仍为抑制作用；当混凝土内部应力由压变为拉时，应力-冻融耦合对混凝土的碳化转换为促进作用。因此我们推测，当混凝土内部的压应力等于某个值时，此时可以使得λFT+P=1，可以称之为冻融临界应力。确定不同冻融条件及混凝土类型下的冻融临界应力，有助于对冻融环境下受碳化混凝土进行有效防护。

白桦林36°坡面径流5.7%，截留94.3%的降雨量；落叶松林17°坡面径流4.8%，截留95.2%的降雨量；2种林分雨水截留相差接近1%[13]。本研究没有36°坡面落叶松林地的径流，但是参考杜阿朋[14]的研究：在同等降雨条件下，华北落叶松产流量陡坡(25°≤a≤36°)16.5 mm、缓坡(10°≤a≤16°)1.5 mm，可以推测落叶松林在36°坡上产流量要远高于白桦林，所以在水源涵养功能上，白桦林高于落叶松林。

表5 冻融-应力耦合作用对碳化程度系数λFT+P的影响Table 5 Effect of freeze-thaw-stress on the coefficient of combination degree λFT+P

3 基于COMSOL的有限元模型分析

3.1 COMSOL在多物理场研究中的应用

COMSOL软件在混凝土耐久性模拟方面分析能力强大，因此在混凝土耐久性研究中得到了广泛的应用[10]。潘晨[11]用COMSOL建立有限元模型，模拟水泥路面板内部结冰情况。Zha等[12]通过建立数学模型，预测混凝土材料的碳化程度并验证模型可用于预测混凝土在超临界条件下的碳化过程。程旭东等[13]采用数值模拟方法，在COMSOL的基础之上，对由于环境不同所造成的温度、湿度和氯离子运输之间的差异进行多场耦合。Rahman等[14]利用COMSOL模拟氯离子快速迁移，对氯离子在损伤混凝土试件中的迁移进行了评价。

多位学者的研究分析证明，使用COMSOL进行的多物理场耦合分析计算准确，与试验结果吻合性较好。因此，选择该软件分析试验梁在碳化、冻融循环、应力共同作用下的反应，具有较高的借鉴意义。

3.2 考虑应力和冻融循环的混凝土碳化数值模型

混凝土碳化过程中，可碳化物质Ca(OH)2(简写CH)、CaCO3(简写CC)、CSH、C3S及C2S各物质质量达到平衡。为建立应力和冻融循环耦合状态下的混凝土碳化数值模型，首先基于Papadakis的经典碳化理论模型[15]，在化学动力学分析方法的支持下，列出微分方程，建立单一碳化数值模型。然后考虑孔隙率与体应变、体应变与荷载的关系，求得冻融循环和应力共同作用下的混凝土孔隙率φs，可由式(6)计算得到。

(6)

其中,φF为n次冻融循环后的混凝土孔隙率，混凝土立方体试块经过冻融水饱和后，在温度为100 ℃的恒温箱里脱水处理直至质量恒定，计算得到失水率，间接测得孔隙率，最终分析回归试验数据得φF=0.030 3e0.002n；θv为混凝土体应变，通过软件定义混凝土材料的本构关系后得出。

再用φs值替换Papadakis模型CO2扩散系数式中的孔隙率φ值，得到考虑冻融循环和应力共同作用下的CO2扩散系数DCO2表达式，见式(7)。

(7)

其中，RH为环境相对湿度。

最终列出偏微分方程，如式(8)所示。其以CO2、CH、CC、CSH、C3S及C2S的质量平衡为条件，建立考虑冻融和应力影响的修正后的混凝土碳化数值模型。

(8)

其中,εα和εw分别为空气、水的体积占混凝土空隙的比例,εα=εw=0.5;Ci为混凝土表面周围i物质的浓度，i为CO2、CH、CC、CSH、C3S和C2S；rC,i为水化物质i的碳化速率，其值为i的浓度、CO2浓度和i的反应常数之积，i为CH、CSH、C3S和C2S;DCH为Ca(OH)2(aq)扩散系数,取DCH=1×10-12m2/s；ϖ为CH的溶解度；rH,i为水化物质i的生成速率，i为CH、C3S和C2S;t为碳化时间。

(9)

边界条件如式(10)所示。

(10)

其中,κ′为冻融循环和应力对Ca(OH)2(aq)扩散系数的影响系数。

3.3 试验结果与模型验证

3.3.1 有限元模型建立

按照以下步骤，建立有限元模型以模拟弯压应力状态下混凝土短梁试件进行冻融-碳化交替试验。

(1)根据短梁试件尺寸在COMSOL中创建几何模型。

(2)根据材料本构关系确定材料属性，施加相应的荷载。

C40混凝土轴心抗压强度fc取26.8 MPa，轴心抗拉强度ft取2.4 MPa，弹性模量Ec取3.25×104MPa，泊松比vc取0.2。混凝土的本构关系(即应力-应变曲线)采用上升阶段结合下降阶段的组合本构关系，混凝土的本构关系公式如式(11)所示。

(11)

其中,σc为混凝土应力；εc为混凝土应变；fc为混凝土轴心抗压强度；ε0为混凝土峰值应变，一般取ε0=0.002；εcu为混凝土极限压应变值，一般取εcu=0.003 3；n为碳化深度。

取n=2，混凝土的本构关系(即应力-应变曲线)如图9所示。

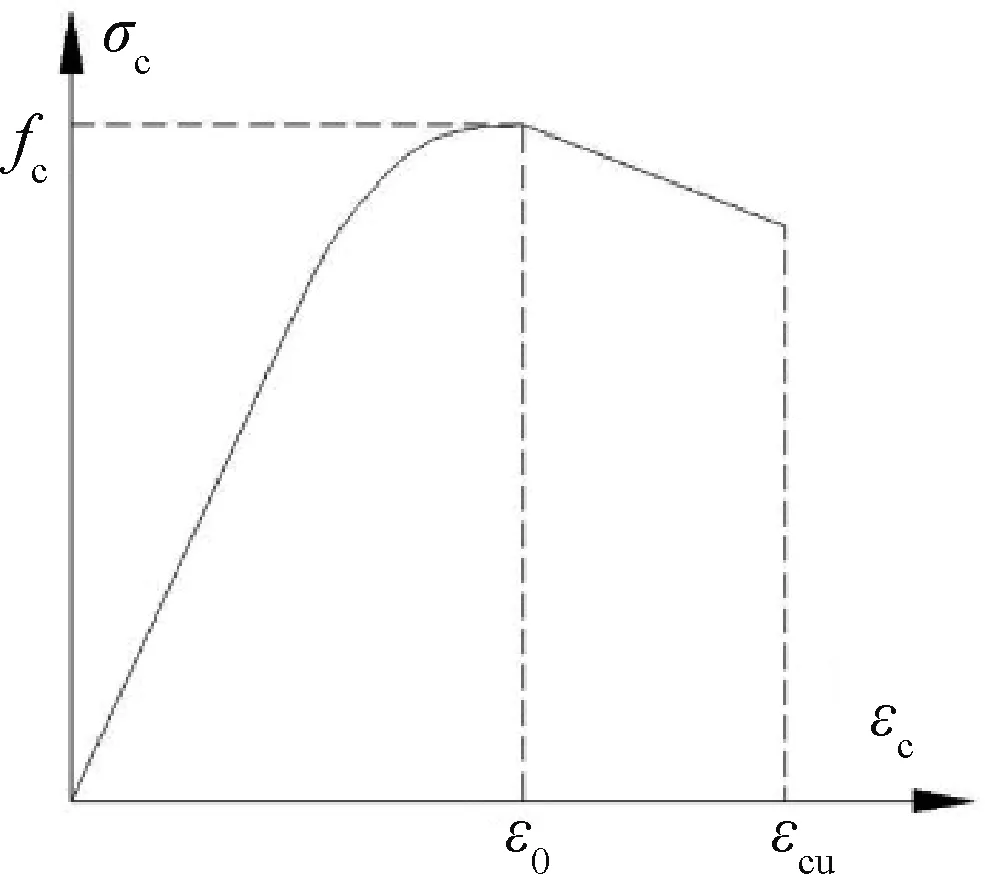
图9 混凝土本构关系
Fig.9 Concrete constitutive relation

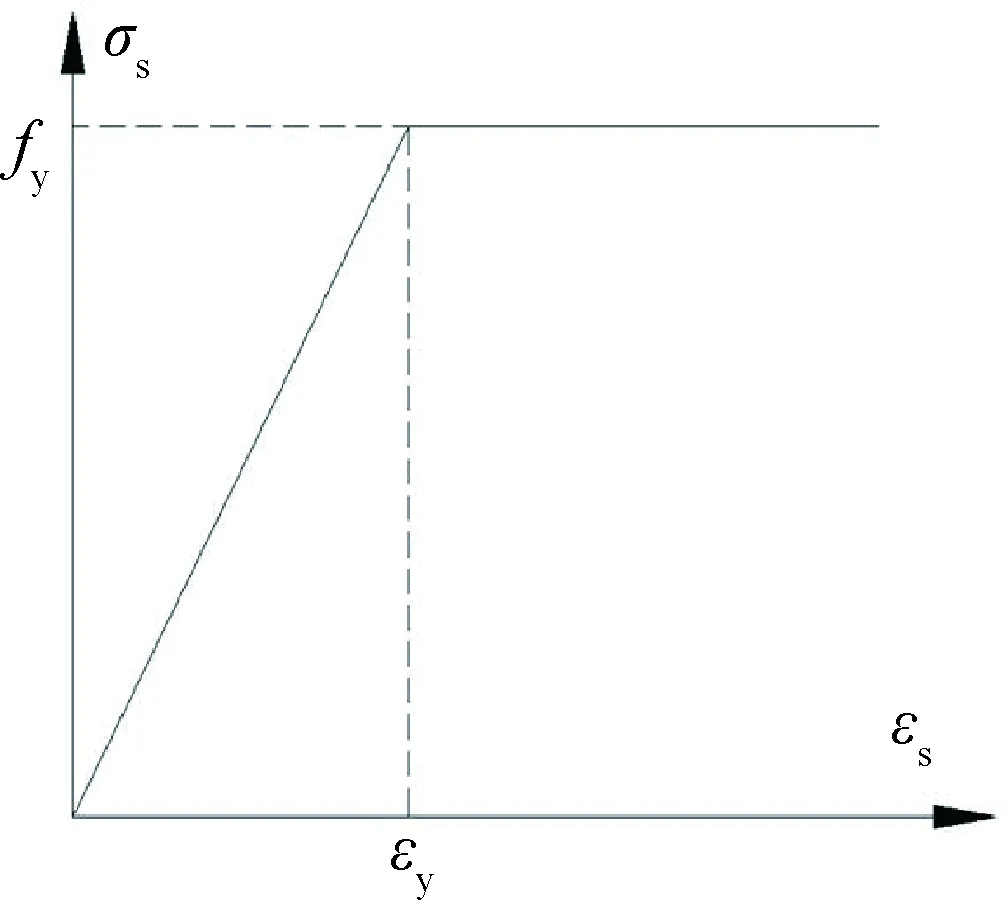
图10 钢筋本构关系
Fig.10 Steel constitutive relation

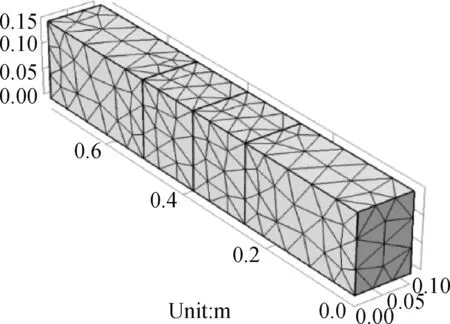
图11 模型网格离散图
Fig.11 Model grid discrete graph

上下缘钢筋型号均为HPB235，屈服强度fy取235 MPa，弹性模量Es取2.1×105MPa，泊松比vs取0.3。钢筋的本构关系(即应力-应变曲线)采用弹塑性简化模型，如图10所示。

(3)模拟冻融-碳化环境，输入冻融循环与应力共同作用下的混凝土碳化数值模型，即公式(8)，并输入CO2扩散系数，即公式(7)。

(4)设立初始条件与边界条件，即公式(9)与公式(10)。

(5)划分网格，运行模型，并对结果进行处理。网格划分情况如图11所示。

3.3.2 有限元分析结果

为描述方便，将弯压应力状态模型视为承受弯压作用的短梁试件，试件配置1号和2号钢筋的一侧分别称为上缘和下缘，长轴方向为纵向，上缘至下缘的方向为竖向。对模型下缘0%fck、15%fck、30%fck三个应力水平的压应力，图12给出应力水平为0%fck的模型空间应力和体应变分布情况；图13以立体和切片的形式给出了应力水平为0%fck的模型碳化深度空间分布情况。

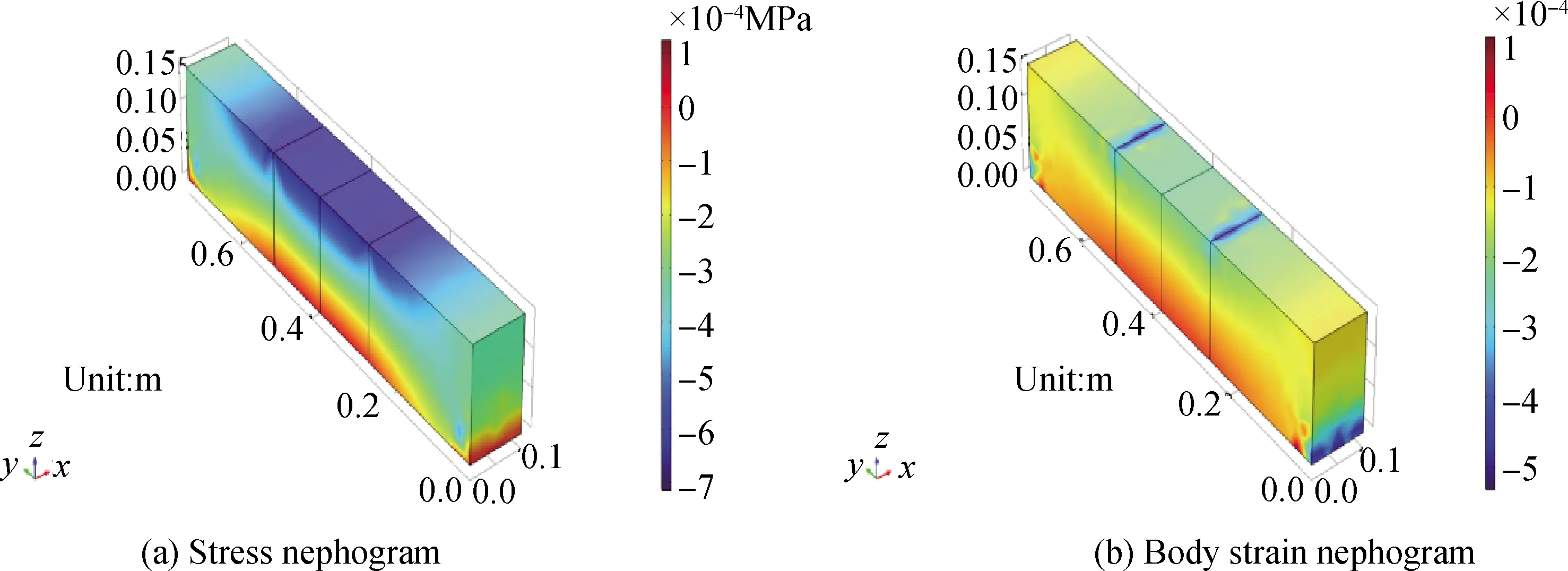
图12 应力和应变分布图Fig.12 Distribution diagram of stress and strain

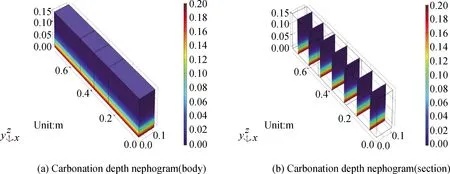
图13 碳化深度图Fig.13 Diagram of carbonation depth

图14分别展示了不同应力水平下试件下缘与梁长及跨中体应变与梁高的关系曲线。从图中可以看出，试件下缘体应变在压应力作用下均为压应变，当应力水平从0%fck增加到30%fck，压应变也随之增加；试件跨中体应变随梁高增加而线性减小，三种压应力水平作用下，跨中体应变在竖向中点处相同，且当应力水平增加，体应变变化速度减小。图15和图16分别展示了不同应力水平下试件孔隙率和CO2扩散系数的变化情况。对比图14～图16发现，孔隙率和CO2扩散系数随试件位置变化趋势与体应变随试件位置变化趋势基本一致，表明三个变量存在着较强的线性物理关系。可以得出结论：相同位置处，CO2扩散系数随着压应力的增大而减小。

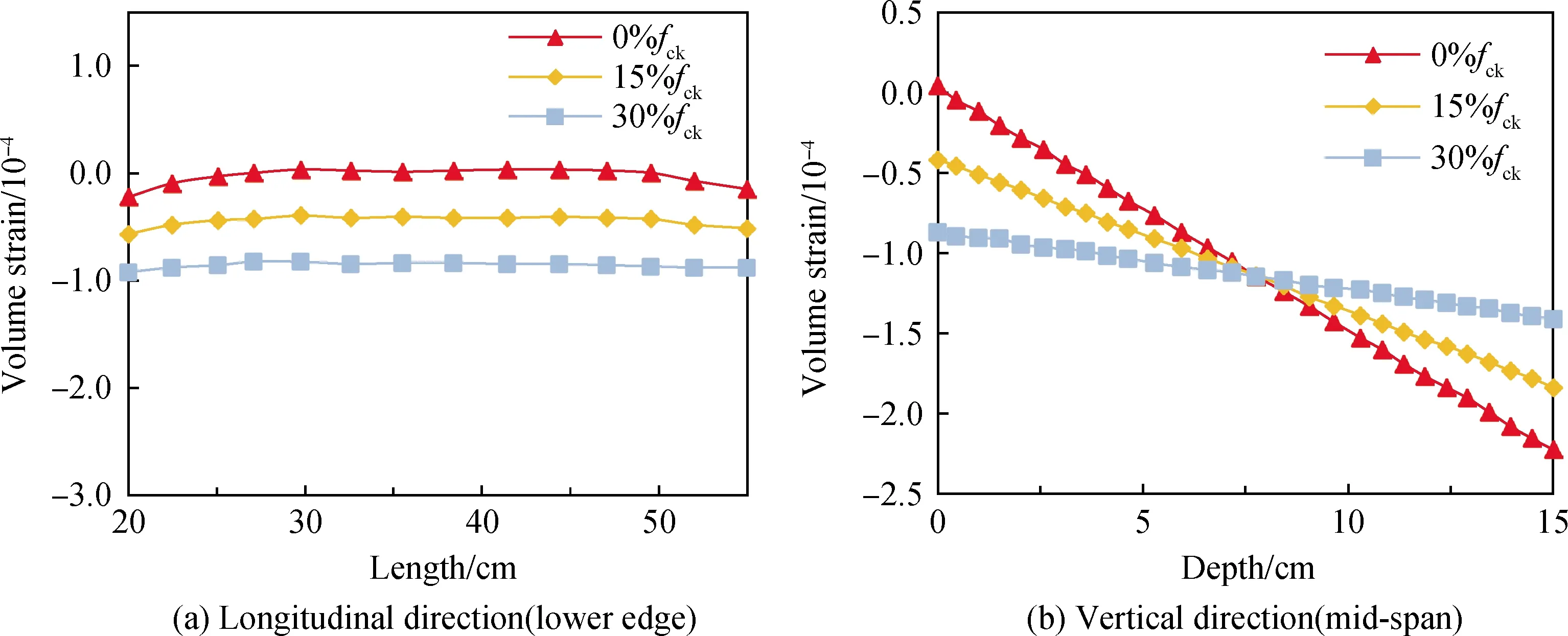
图14 不同应力水平梁体应变变化Fig.14 Volume strain variations of beams at different stress levels

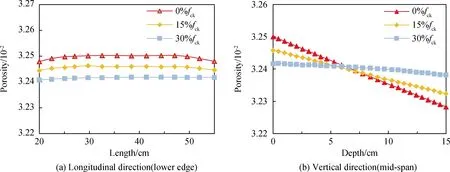
图15 不同应力水平梁孔隙率变化Fig.15 Porosity variations of beams at different stress levels

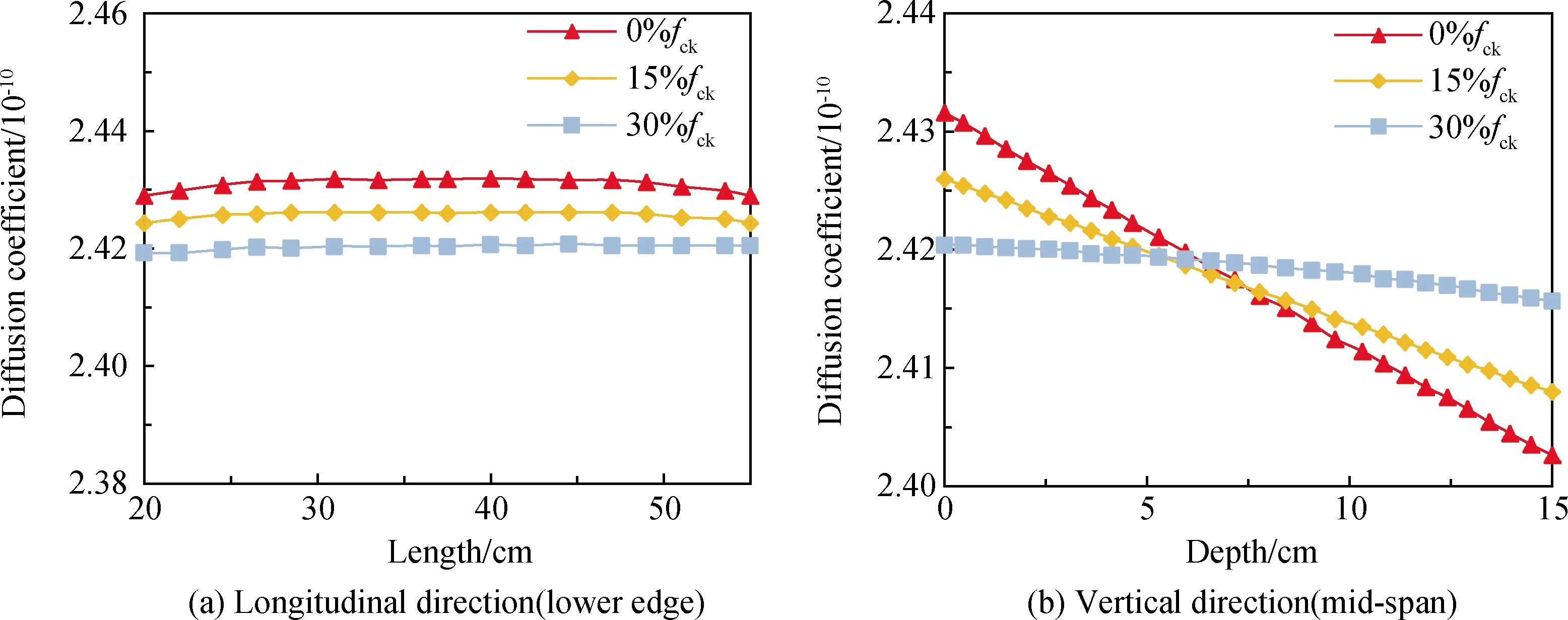
图16 不同应力水平梁CO2扩散系数变化Fig.16 CO2 diffusion coefficient variations of beams at different stress levels

3.3.3 试验与有限元结果对比

图17给出了碳化深度模型计算值与试验实测值的对比结果。由该图可知，两者数据吻合性较好，证明该模型可靠性较高。由此，我们有更充分的证据给出压应力增强混凝土抗碳化能力的机理解释：试验梁被施加压应力时，同一位置处混凝土体应变减小，孔隙率减小，CO2进入混凝土内部的难度增大，CO2扩散系数减小，因而短梁的混凝土抗碳化能力增强，且压应力越大，增强作用越明显。

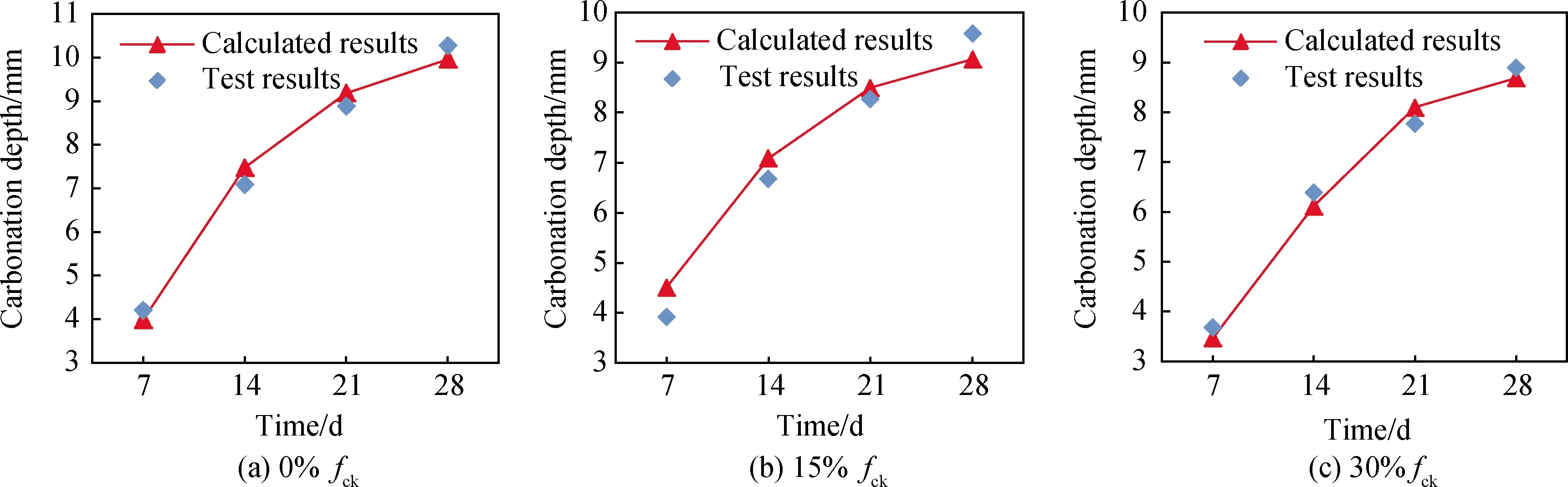
图17 碳化深度计算值与实测值对比Fig.17 Comparison between calculated value and tested value of carbonation depth

4 结 论

(1)混凝土试件受压时，压应力增强混凝土抗碳化能力，且承受压力越大，增强作用越明显；混凝土处于冻融循环环境中，抗碳化能力降低，且冻融对混凝土碳化的促进作用均匀增加。

(2)当混凝土内部应力由压应力变为拉应力时，应力-冻融耦合作用对混凝土的碳化影响由抑制转换为促进作用。当混凝土内部压应力等于某个值时，应力与冻融对混凝土的碳化作用产生中和。因此，可以通过控制应力水平来控制混凝土的碳化速率以达到对混凝土结构的碳化防护。

(3)弯压应力状态下，钢筋混凝土梁冻融-碳化试验有限元分析结果说明，随着压应力增大，钢筋混凝土梁体应变减小，孔隙率降低，导致CO2扩散系数减小。

(4)梁“弯压加载+碳化-冻融交替试验”实测结果与有限元分析结果吻合性较好，说明建立的弯压应力状态梁冻融-碳化数值模型可靠性较高，可为冻融环境下持荷状态混凝土构件碳化深度预测分析提供依据。