FSC赛车车架的结构分析与轻量化设计

戴波棋 李长江

温州大学机电工程学院，中国·浙江 温州 325000

FSC 赛车车架；有限元分析；灵敏度；轻量化设计

1 引言

车架作为赛车的装配基体，连接车架与各总成和零件并承受传递给车架的力和力矩。车架质量约占赛车整备质量的15%[1]，对车架进行轻量化设计可提高赛车的动力性和燃油经济性。通过有限元模型的分析和优化，改进车架的强度、刚度并减轻它的质量。

景陶敬[2]等人对模型进行强度和刚度分析，可得到不同工况下车架的受力和变形情况。基于足够的强度和刚度条件下，固有频率是研究结构动态性能的重要参数。郭潇然[3]等人研究了车架的固有频率和振型，以避免车架的共振特性和保证良好的动态性能。在为赛车的安全性提供理论依据后，刘越辉[4]通过灵敏度分析计算车架刚度、固有频率对设计参数的敏感度。论文通过灵敏度分析改变钢管壁厚，以达到轻量化的设计要求。刘文杰[5]等人通过拓扑优化和尺寸优化等方法实现车架的轻量化。

论文通过Hypermesh 有限元分析建模，计算分析车架强度、扭转刚度及固有频率，基于车架的可靠性，减轻车架质量来提升赛车的性能。

2 车架三维模型设计

车架设计使用CATIA 建立三维模型，采用不同尺寸的4130 钢管完成车架设计，车架结构设计需满足人机工程，以及各总成和零件的安装空间需求和后期拆装的便捷性，保证车手驾驶时视野的开阔性，提高驾驶的舒适性和安全性。基于赛事规则要求，完成车架CATIA 模型设计。

3 车架有限元模型建立

将CATIA 模型导入Hypermesh，创建片体模型。为提高车架的精准度，对车架进行高质量的网格划分，使用混合网格，设置车架网格尺寸为4mm。为简化模型结构，使用刚性约束的方式模拟焊接。使用壳体命令赋予片体厚度，完成车架有限元模型的创建。

以轮胎中心创建硬点用于施加约束条件，为了方便添加驾驶员、动力总成和传动系统的载荷，创建3 个硬点用于施加均布载荷，最终得到的车架有限元模型如图2所示。

4 车架强度分析

根据比赛规则，赛车在比赛中需要完成直线加速、8 字绕环和高速避障等不同赛道比赛[6]，为保证赛车的安全性，需对车架进行弯曲强度、扭转刚度的校核。论文通过满载弯曲、紧急制动、起步加速和高速转弯4 种工况，对车架的位移、应力和扭转刚度进行分析。

4.1 满载弯曲工况

满载弯曲工况分析的是赛车在满载状态下，在良好路面上静止或匀速直线行驶时车架的弯曲变形及应力分布情况。对车架约束受力点，并施加载荷，约束左前轮Z 方向移动，右前轮Y、Z 方向移动，左后轮Z 方向移动，右后轮Y、Z 方向移动。

图1为满载弯曲工况应力云图，最大应力为224.6MPa，最大应力所在的位置是发动机上吊耳固定杆左侧支撑杆与主环斜撑等杆件焊接的交汇处。

图1 满载弯曲工况应力云图

4.2 紧急制动

赛车在行驶过程中遇到紧急情况需要进行紧急制动时，车架会产生一个向后的制动减速度as，即水平向前的惯性力。假定减速度大小为恒定值，则减速度as的计算公式为：

上式中：as——制动减速度，m/s2；V1——制动初速度，m/s；S——制动距离，m。

以FSC 赛车为例计算制动减速度。取制动初速度为V1为80m/s，制动距离S 为30m，带入公式（1）计算得制动减速度为8m/s2，即0.8g。

论文模拟紧急制动过程中，前轮完全抱死，约束前轮X、Y、Z 移动，后轮Y、Z 移动。除了添加车架自重，使用重力加速度施加一个沿运动相反方向的制动减速度as=0.8g。

计算所得的车架应力云图如图2所示。

图2 紧急制动工况应力云图

4.3 起步加速工况

起步加速工况是对加速状态下的车架进行强度校核，主要模拟赛车在条件良好的路面条件下，启动并快速加速时，车架的变形情况和应力分布。在赛车加速的过程中，还会在加速路径上受到一个惯性力的作用，得到一个启动加速度af。假定加速度大小为恒定值，则加速度af 的计算公式为：

上式中：af——加速度，m/s2；t——加速时间，s；S——加速距离，m。

以FSC 车做75m 直线加速项目为例计算加速度。近似认为赛车做匀加速直线运动，加速距离S 为75m，加速时间t 为6s，带入公式（2）求得加速度af为4.2m/s2，即0.42g。

论文模拟起步加速过程中，后轮完全抱死，约束前轮Z移动，后轮X、Y、Z 移动。使用重力加速度施加一个沿运动相同方向的加速度af=0.8g。图3为计算所得的起步加速工况应力云图。

图3 起步加速工况应力云图

4.4 高速转弯工况

赛车在高速转弯过程中，载荷在离心力的作用下发生横向转移，论文以向左转向为例，产生一个侧向加速度ac。侧向加速度ac的计算公式为：

上式中：ac——侧向加速度，m/s2；r——赛道半径，m；t——单圈时间，s。

以FSC 赛车做8 字环绕项目为例计算侧向加速度。实际获得最快单圈时间为6s，赛道半径r=9.125m,带入公式（3）求得ac为10.0m/s2，即1g。

模拟左转向过程中，约束左前轮X、Y、Z 移动，右前轮Y、Z 移动，后轮Z 移动。通过重力加速度添加水平向左的侧向加速度ac=1.0g。图4为计算所得的高速转弯工况应力云图。

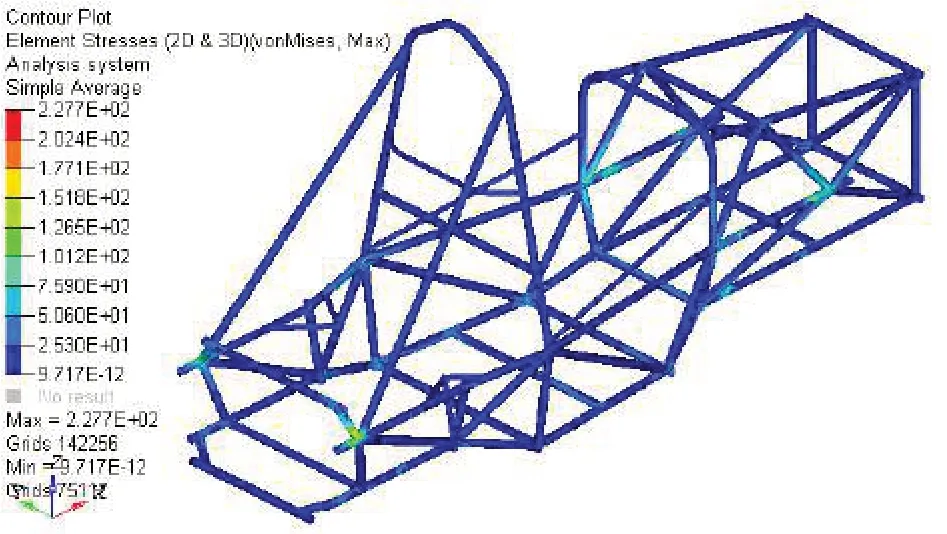
图4 高速转弯工况应力云图

5 车架刚度分析

扭转刚度是车架的一个十分重要的力学性能评估指标，是衡量车架性能的一个重要参数，对车架的优化设计具有重要的指导意义。约束右前悬与车架连接的4 个吊耳的X、Y、Z 移动，约束后悬与车架连接的8 个吊耳的X、Y、Z 移动，释放左前悬自由度，同时在车架左前悬上A 臂安装杆上施加沿Z 轴负向，大小为1000N 的力。查看该工况下的位移，如图5所示。

在该扭转工况下，右侧悬架上A 臂连接杆为约束端，其变形量为0，左侧悬架上A 臂连接杆为加载端，其最大变形量h 为1.241mm，两平行杆件的中心距L 为460mm，载荷F为1000N，根据扭转刚度计算公式：

带入上述数据后得到车架的扭转刚度CT为2975.92Nm/deg，该车架满足扭转刚度要求。

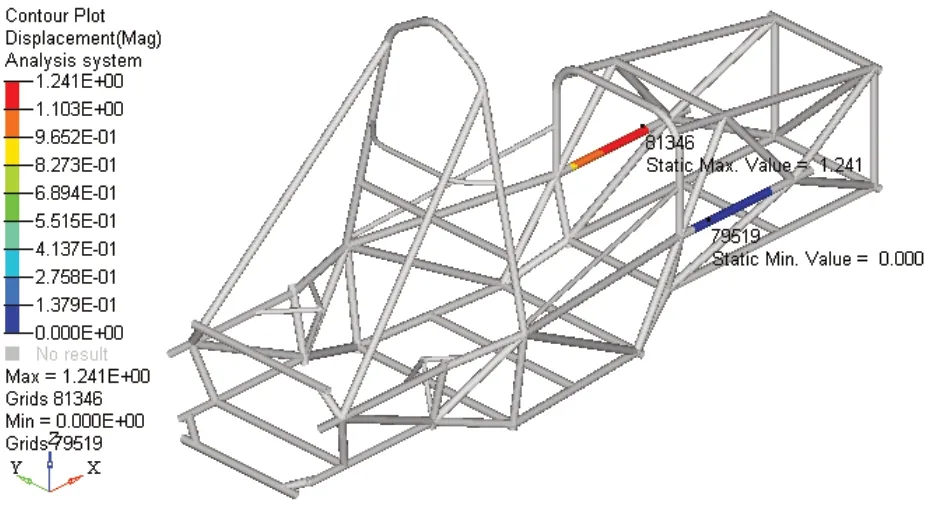
图5 扭转工况下两杆件的位移云图

6 车架模态分析

当赛车在赛道上行驶的时候，可能引起车架共振的主要有路面和发动机两种振源。路面不平度产生的随机振动频率一般为20Hz，论文选用HONDA 的CBR600 F4i 发动机，其怠速频率为30Hz 左右，驾驶频率在160 ～240Hz 之间[7]。为避免出现共振现象，需要对车架的固有频率和振型进行分析。车架前六阶固有频率的分析结果如表1所示。其固有频率范围在39.82Hz～100.05Hz，很好的避开了路面和发动机的振动频率，该车架设计较为合理。

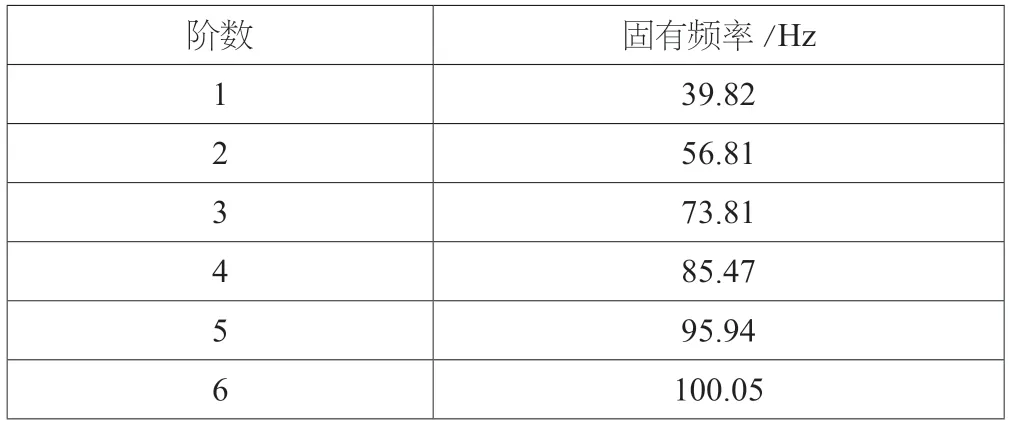
表1 车架前六阶固有频率

7 灵敏度分析

论文选取车架全部管件的壁厚作为待选变量，然后通过分析各管件壁厚对1 阶模态频率、扭转刚度和质量的灵敏度系数，进行变量筛选[8]。计算1 阶模态频率和质量的灵敏度系数，计算结果见表2。

表2 计算结果输出表

优化后的车架应以力学性能条件和低阶固有频率不明显低于基准模型为要求。选取1 阶模态频率和扭转工况下加载点的综合变形量作为约束条件，得到约束函数为：

上式中：D1——扭转工况下加载点的位移，mm；f1——1 阶模态频率，Hz。

车架质量从最初的32.4kg 下降到27.8kg，减重4.6kg，降幅达到14.2%

8 结论

论文对FSC 赛车车架展开对象，重点借助有限元软件对所设计车架进行了多工况下的强度和刚度校核以及使用灵敏度分析法实现了车架的轻量化设计。研究内容如下：

（1）通过分析可见，该车架在各工况的最大变形最大应力远小于材料的屈服极限，充分满足 FSC 各赛道的安全要求。

（2）校核计算车架刚度由2975.92Nm/deg 降为2129.83Nm/deg，仍处于FSC 赛车车架扭转刚度的中上水平

（3）整个设计从最初的32.4kg 下降到27.8kg，降幅达到14.2%