季节冻土区公路隧道三维温度场时空分布规律

张玉伟，宋战平，赖金星，李又云

(1.西安建筑科技大学 土木工程学院，陕西 西安 710055；2. 西安建筑科技大学 陕西省岩土与地下空间工程重点实验室，陕西 西安 710055；3.长安大学 公路学院, 陕西 西安 710064)

0 引言

我国高纬度和高海拔地区均属于典型的季节性冻土区，这些地区温度周期性变化常常对建筑物造成冻融损害[1-5]。对于隧道工程而言，衬砌容易发生冻胀破坏，出现衬砌漏水、路面结冰等冻害[6-10]。探明隧道温度场规律是解决冻害的前提。丁浩[11]等通过现场测试分析了隧道围岩和衬砌温度变化规律；张学富[12]等自编程序分析了风火山隧道环境-围岩热传导变化规律；谭贤君[13]等考虑通风影响，推导了围岩温度场模型；Li[14]等分析了隧道开挖后围岩温度场的分布、初期支护以及二次衬砌的温度变化规律；Zhou[15]等基于季节冻土隧道，建立了保温层优化计算模型；Zhang[16]等研究了热棒在浅埋寒区隧道工程中应用，并分析其温度变化特性；Zeng[17]等分析了对流传导耦合效应下的隧道温度场变化规律；Jun[18]等采用现场测试手段分析了隧道内部冬季温度变化规律。寒区隧道冻害是冻胀力周期性作用于衬砌，导致衬砌疲劳劣化而出现病害，冻胀力又由于温度变化而产生。因此建立隧道三维温度场模型、明确温度演化规律是解决寒区隧道冻害问题的基础。

关于寒区隧道温度场研究多以数值模拟手段为主，基于现场测试的温度场研究则相对较少，且测试数据完整性尚显不足，在现场测试基础上进行三维温度场的研究更是很少涉及。为建立寒区隧道三维温度场模型，本研究采用温度传感器开展了现场监测，获得隧道环境温度和围岩温度变化规律，并推导了围岩冻结深度随隧道进深和时间的变化规律。通过测试结果分析，建立了三维温度场数学模型，模型可以预测温度场的时空变化特征，研究结果可为寒区隧道保温设计提供依据，也为进一步研究冻胀力提供了基础。

1 现场测试分析

1.1 工程概况

某寒区公路隧道位于川西高原，海拔高程4 200 m 左右，隧道长度2 745 m，为单洞双车道的二级公路隧道，隧道断面净空尺寸(宽×高)为 9 m×5 m。隧址区属于青藏高原气候，夏季温和，冬季寒冷，极端高温超过30 ℃，极端低温低于-20 ℃。5月至10月多为东南风，最大风速大于5.7 m/s，频率27%；11月至次年4月多偏北风，最大风速20 m/s，平均风速4 m/s，频率23%，隧道内风速多为3～5 m/s。隧址区域内水系发育，受围岩温度场变化，发生冻害的可能性较大。

1.2 测试方案

隧道温度场主要指洞内环境温度场和围岩温度场，因此测试主要针对洞内温度和围岩温度展开，隧道洞口段气温变化明显，而越往隧道内部，温度变化越小，因此主要布置在洞口段，第1个断面位于洞口处，依次向内分别间隔20，30，50 m和100 m。断面布置见图1和图2，其中5个测试断面均进行环境温度测试，选取断面1和断面4进行围岩温度测试，围岩温度传感器采用湖南某公司生产的YH5101型温度传感器。主要技术参数为：理论可工作温度区间为-50～50 ℃，灵敏度为0.1 ℃。布设方法为在围岩打4 m深的孔，将温度传感器间隔1 m 固定在1根钢筋上，然后插入到孔中，用砂浆回填(见图2)。采用某公司配套的自动化采集系统，围岩内温度值监测频率为每天4次，测定时间为每天2：00，8：00，14：00，20：00。

图1 测试断面Fig.1 Test section

图2 围岩温度测点布设Fig.2 Layout of temperature measuring points on surrounding rock

1.3 测试结果分析

隧道环境温度通过温度计直接测得，取每月中日平均温度的均值作为隧道环境温度的月平均值。图3和图4分别给出了不同断面环境温度随时间和进深的变化规律。图3可以看出5个断面的环境温度均呈正弦函数规律变化，但5个断面的最高温度和最低温度不同，即正弦函数的振幅不同，图4表明隧道洞口段温度随时间变化更加明显，越往隧道内部，温度变化越小，即温度振幅随着隧道进深增加而逐渐趋于稳定，说明隧道具有一定自保温效果，洞口段应着重保温。

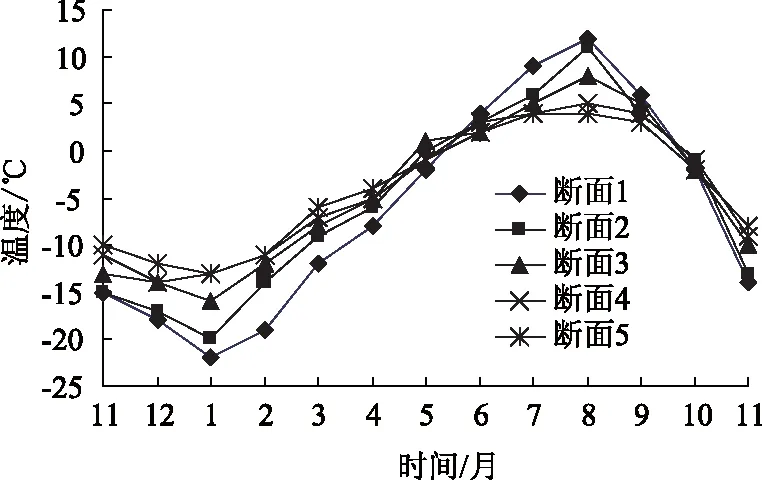
图3 环境温度随时间变化Fig.3 Ambient temperature varying with time

图4 环境温度随进深变化Fig.4 Ambient temperature varying with length

取每月日均温度的平均值作为月平均温度，图5给出了断面1不同径向深度围岩温度随时间变化规律，图6给出了围岩温度随径向深度的变化规律。图5表明某一断面处围岩径向温度受环境温度的影响也呈正弦函数变化，且隧道围岩径向深度的增加影响效果逐渐减小，越靠近衬砌表面正弦规律变化越明显，测点4,5温度基本不变说明径向深度达到3 m时基本不受影响，温度影响范围主要集中在距衬砌2 m范围内。图6表明围岩温度随径向深度的变化关系，在围岩受影响的2 m范围内负温月份的温度与径向深度近似呈线性关系，随着深度增加温度逐渐趋于原始围岩温度。

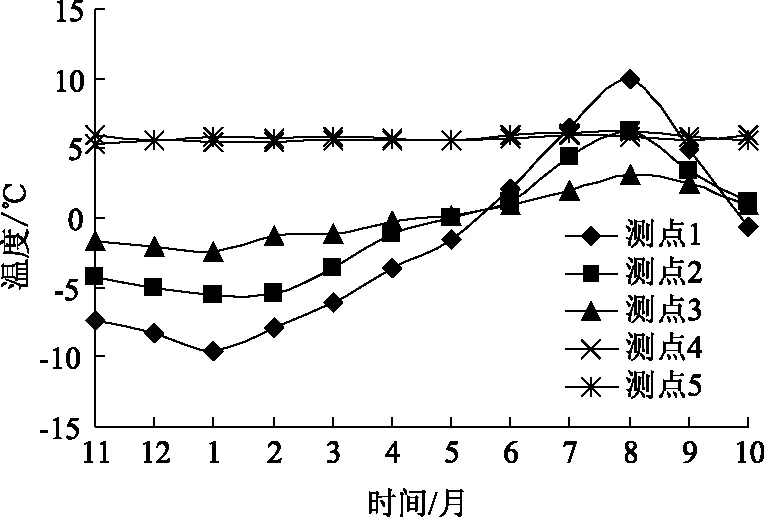
图5 围岩温度随时间变化Fig.5 Temperature of surrounding rock varying with time

图6 围岩温度随径向深度变化Fig.6 Temperature of surrounding rock varying with radial depth

2 温度场时空分布模型

2.1 环境温度场

通过分析结果可看出环境温度随时间呈正弦规律变化，环境温度可表达为[7]：

(1)

式中，Tm为某一断面的温度；T0为平均温度；A0为振幅；t为月份；t0为相位。式(1)即描述了环境温度随时间的正弦函数演化特征，式(1)中未涉及隧道进深，由测试结果我们知道T0和A0均随隧道进深变化而改变，如果得到T0和A0随隧道进深的函数关系，并代入式(1)即可得到环境温度的时空变化规律。下面根据现场测试数据分析T0和A0与隧道进深的变化关系。

表1给出振幅A0与平均温度T0随隧道进深变化规律，为了得到近似函数关系，采用非线性拟合回归分析得到两者随隧道进深的函数表达式，通过拟合图7为近似拟合效果，通过图7可看出，平均温度随隧道进深呈近似线性关系，振幅随隧道进深呈近似对数关系，可采用线性函数和对数函数近似描述评价温度和振幅，见式(2)，式(3)。

表1 振幅与平均温度随进深的变化Tab.1 Amplitude and average temperature varying with length

图7 环境平均温度和振幅Fig.7 Average ambient temperature and amplitude

Ay=alnx+b，

(2)

Ty=cx+d，

(3)

式中，a,b,c,d分别为拟合值，本研究中a取-3.96，b取 29.14，c取0.007 3，d取-5.14；x为距洞口距离。将式(2)，式(3)代入式(1)得：

(4)

式(4)即为隧道环境温度时空分布规律(图8)。

图8 环境温度场时空分布图Fig.8 Spatial-temporal distribution of ambient temperature field

2.2 围岩径向温度场

围岩温度场受环境温度的影响，变化规律较为复杂。围岩温度场可通过传热学原理推导得出严格的解析解[13-14]，但需要做诸多假设，且推导过程繁琐，结果表达也相当复杂，实际应用不是很方便，本研究从实用的角度出发，依据现场测试结果，旨在给出围岩温度场的拟合经验公式，文献[7]做过类似的工作，但是只给出了某一断面处围岩温度沿径向的变化规律，没有建立围岩温度场与轴向深度时间的三维关系。本研究通过围岩温度测试成果，建立围岩温度场表达式。围岩温度与隧道进深、时间和围岩径向深度3个变量有关，属四维问题，而围岩温度与环境温度密切相关，因此首先建立围岩温度与环境温度的关系，即暂不考虑隧道进深的影响，减少一个变量。

由图5可看出径向一定深度范围内围岩温度也呈正弦函数规律变化，即围岩温度场也可以用式(1)描述，考虑某一断面处围岩温度场，围岩平均温度和振幅与径向深度的关系见表2，并将两者关系绘制于图9。

图9中可看出围岩平均温度和振幅均随径向深度有一定关系，文献[9]也指出年温度振幅随围岩径向深度呈指数规律降低，一定深度后振幅为0，围岩平均温度呈对数规律变化，因此文中假定以上规律进行拟合：

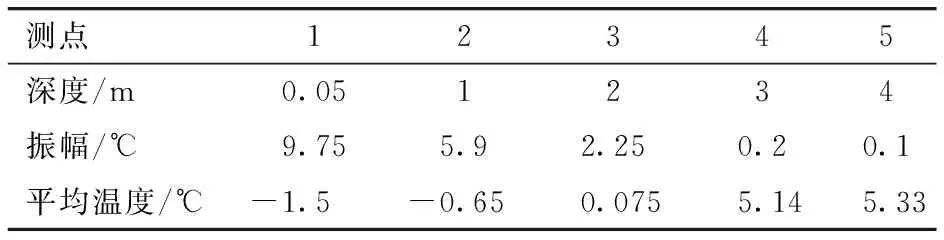
表2 振幅与平均温度随径向深度的变化Tab.2 Amplitude and average temperature varying with radial depth

图9 围岩振幅与平均温度Fig.9 Amplitude and average temperature of surrounding rock

Aw=a′exp(b′r)，

(5)

Tw=c′lnr+d′，

(6)

式中，a′,b′,c′,d′分别为拟合值，文中a′取13.42，b′取-1.13，c′取1.48，d′取2.26，r为围岩径向深度Aw为围岩的平均温度。将式(5)～(6)代入式(1)得：

(7)

式中,Tw为某一断面处围岩温度随径向深度和时间的变化规律;t′0为围岩温度月相位。

可以看出，式(7)给出了某一断面处围岩温度与时间和围岩径向深度的关系，并未建立与隧道轴向深度的关系，我们知道围岩温度与环境温度密切相关，而环境温度沿隧道进深关系为对数关系，因此假设围岩温度与轴向深度关系也呈近似对数关系：

Tw(x)=αlnx+β，

(8)

式中α,β为拟合参数。式(7)和式(8)共同建立了围岩温度与时间、径向深度、隧道轴向深度的关系。

事实上我们主要关心围岩冻结月份(11月至次年3月)的温度变化，分析图6可以看出，围岩冻结月份温度随径向深度增加逐渐增大，在2 m范围内可近似认为是线性的，随着径向深度进一步增大，温度逐步趋于原始围岩温度。因此可假设围岩在受影响的范围内温度也是近似线性变化的，可直接建立围岩温度与环境温度的关系。

Tw=k1Tm+k2r，

(9)

式中，k1为热量散失及滞后效应引起的温度损失系数；k2为拟合系数；r为围岩径向深度。其中k1可通过数值分析或室内试验进行确定。

2.3 冻结深度的确定

在温度场基础上可进一步确定围岩冻结深度，从而为冻胀力研究和防冻保温设计提供理论依据，在季冻区围岩的冻结深度可由Stephen公式确定：

(10)

Qw=qρd(ω-ωc)，

(11)

式中，hw为冻深；λw为导热系数；∑Tw为冻结指数；Qw为单位体积相变潜热；q为水结冰相变潜热；ρd为干密度；ω为总含水率；ωc为含冰量。

式(10)表明围岩冻结深度与围岩冻结指数相关，而围岩冻结指数与隧道环境温度有关，隧道环境温度具有时空变化特征，可由式(4)来表示，温度变化见图10。式中，x1=(12/2π)arcsin[-(cx+d)/(alnx+b)]，围岩冻结指数可由积分求得：

图10 温度变化示意图Fig.10 Schematic diagram of temperature change

(12)

联立式(11)～式(13)可得围岩最大冻结深度随隧道深度的变化：

(13)

式(13)即为围岩冻结深度随隧道进深的变化关系，但无法描述冻结深度随时间的变化关系，实际中围岩冻结深度与环境温度密切相关，前述分析表明隧道环境温度随时间呈正弦规律变化，因此，可近似认为围岩冻结深度也随时间呈正弦规律变化，即：

(14)

式(13)和式(14)即描述了围岩冻结深度随隧道进深和时间的变化规律。

3 结果对比分析

3.1 环境温度

图11和图12分别给出环境温度随时间变化规律和空间变化规律的模型计算值与实测值对比，可以看出计算值与实测值总体吻合较好，随轴向深度温度变化幅度逐渐减小，不同深度的平均温度与振幅拟合函数能够很好地描述环境温度变化，随进深增加有自保温效果，保温设计时应予以考虑。

图11 环境温度随时间变化对比Fig.11 Comparison of Ambient temperatures varying with time

图12 环境温度随进深变化对比Fig.12 Comparison of Ambient temperatures varying with length

3.2 围岩温度

图13和图14为围岩温度随时间和围岩径向深度的对比，可看出受环境温度的影响围岩径向一定范围内温度也呈正弦规律变化，随径向深度增加变化逐渐减小，距离衬砌表面越近变化越明显，模型预测值与现场测试值吻合较好，说明本研究模型能够准确预测围岩温度随时间和围岩径向深度的变化规律，通过模型可初步预测某一断面处围岩径向温度。

图13 围岩温度随时间变化对比Fig.13 Comparison of surrounding rock temperatures varying with time

图14 围岩温度随径向深度变化对比Fig.14 Comparison of surrounding rock temperatures varying with radial depth

3.3 冻结深度

由设计资料，λw取1.12，平均气温T0为1.1 ℃，温度振幅A为年温度差一半取18 ℃，水结冰相变潜热q为333.56 kJ/kg，围岩干密度ρd为2.35 kg/m3，围岩总含水率ω为46.2%，冻结围岩中含冰量ωf为41.7%，由式(13)求得围岩冻结深度。图15为围岩冻结深度随隧道轴向深度的变化规律，冻结深度随轴向距离的增加而逐渐减小，断面1为1.83 m，断面5为1.45 m，由前文环境温度结果可以看出越往隧道内部环境温度越高，隧道有一定的自保温效果，因此围岩冻结深度逐渐减小，与模型计算结果相吻合；通过断面1和断面4的围岩温度测试结果也可以看出，因为断面4位于隧道内部，断面1围岩冻结深度要大于断面4，这也与模型计算结果相一致。

图15 冻结深度随轴向距离变化Fig.15 Frozen depth varying with axial distance

现场测试和模型计算结果说明，寒区隧道洞口段环境温度受环境温度影响周期性变化明显，随着轴向深度的增加，温度振幅减小，隧道有自保温效果，围岩温度在径向一定范围内受环境温度的影响也呈正弦函数周期性变化，这种影响随着围岩深度增加逐渐减弱，影响范围主要集中在2 m范围内，基于温度场进一步求解围岩冻结深度，其规律在空间上表现为随着轴向深度增加逐渐减小，隧道洞口段应加强保温措施。温度场分布规律一方面为寒区隧道保温设计提供理论依据，另一方面也为下一步研究冻胀力提供了理论基础。

4 结论

(1)依托某寒区隧道工程现场布设若干测试断面，分别测试了隧道洞内温度、围岩径向温度，结果表明，隧道洞内温度与时间和轴向距离呈三维变化关系，同一断面温度与时间呈正弦函数变化，同一时间时平均温度与轴向距离呈线性变化，温度振幅与轴向距离呈对数变化，隧道洞内温度在洞口段200 m范围内变化剧烈，围岩温度在2 m范围内变化明显。

(2)以现场测试成果为基础建立寒区隧道洞内温度场时空分布模型和围岩径向温度场模型，在此基础上分析围岩冻结深度变化规律，洞口处断面1最大为1.83 m，随着隧道进深增加，围岩冻结深度逐渐减小,断面5仅为1.45 m，与现场测试结果基本吻合。

(3)建立了三维温度场模型，当类似寒区隧道缺乏温度实测资料时,可根据本研究的方法对温度场进行初步预测。文中计算模型中的参数是根据本隧道测试结果得出的，对于气候条件相似的寒区隧道具有一定的适用性，但是对于气候温度相差较大的隧道具有局限性，建议以后有条件增加温度场测试工作，对模型中参数进一步修正，并建立气候温度条件与模型参数的对应关系，使其具有更广泛的适应性。