基于2S2P1D模型的沥青混合料老化前后黏弹性参数演变
马昊天,范立嘉,李思童,张业兴,郭昱涛
(1.北京建筑大学 土木与交通工程学院,北京 100044;2.北京市南水北调干线管理处,北京 100195;3.北京市政路桥建材集团有限公司房山沥青厂,北京 102488;4.北京大学第一医院,北京 100034;5.北京建筑大学 未来城市设计高精尖创新中心,北京 100044;6.北京建筑大学 北京市交通基础设施建设工程中心,北京 100044)
0 引言
沥青路面在使用过程中,由于受到热、氧、紫外光照射、雨水冲刷等环境因素以及重复荷载的作用,沥青混合料会发生一系列不可逆的物理化学变化,导致其性能劣化即老化,老化现象使得路面尚未达到设计使用年限就产生各种病害[1]。目前实验室模拟沥青混合料老化主要采用热氧老化的方法,美国(AASHTO)和我国规范中均采用烘箱老化法,包括短期和长期烘箱老化法。短期烘箱老化法(Short-Term Oven Aging, STOA)是对松散状态混合料进行135 ℃烘箱加热4 h后压实成型,以模拟沥青混合料在施工现场拌和和铺筑过程中的老化,而长期烘箱老化法(Long-Term Oven Aging, LTOA)则是对短期老化并成型后的沥青混合料试件进行85 ℃烘箱加热5 d,以模拟沥青路面使用5~7 a的老化过程[2-3]。尽管SHRP中提出的老化方法没有考虑光照、降雨等外界因素的影响,无法完全模拟实际路面的老化状态[4],但仍能在室内模拟老化和实际老化之间建立合理的联系[5-6],且大量研究表明采用室内老化的混合料进行各项试验探究实际老化混合料的老化性能是十分有效的[7-8]。
与此同时,大量基于上述老化方法对沥青混合料性能的变化研究中发现沥青混合料老化后的高温稳定性有所提高,但水稳定性、低温抗裂性能和疲劳性能显著降低[9-12]。然而,研究多基于静载试验,考虑到沥青混合料是一种由沥青及集料组合的混合物,由于沥青的黏弹性特征,故沥青混合料力学性能与温度及频率关联密切。Arefin、马莉骍[13-14]等利用动态模量试验探究了不同沥青混合料老化后的动态力学性能,并考虑了温度和荷载频率对动态模量和相位角的影响,结果表明老化后沥青混合料的动态模量增大,相位角减小,另外,考虑到实际试验过程中加载的频率及试验温度不可能无限扩展,研究者利用Sigmodal函数建立了动态模量主曲线,并对老化后动态模量在整个温度和频率范围内的变化情况进行了研究,虽然发现老化使得沥青混合料的温度敏感性减小,但该研究未从本构关系的角度考虑沥青混合料在老化前后的黏弹性能演变特征。
基于沥青混合料动态模量对沥青混合料力学本构关系表征现阶段主要分为数学模型及物理模型,数学模型以CA及CAM模型为代表,但已有研究发现该模型无法对低频率的数据进行良好的拟合。物理模型则以Maxwell、Kelvin-Vogit及Burgers模型为代表[15]。以Maxwell为例,其以一个弹簧和一个黏壶串联得到,可以很好地表征沥青混合料的蠕变过程,但是模型因为过于简单,无法准确地描述沥青及其混合料的黏弹性变化规律。于是,研究者们在此基础上建立了衍生的Maxwell和Kelvin模型(多个Maxwell原件并联或多个Kelvin原件串联),其可较好地表征沥青这种黏弹性材料在动态荷载的响应规律,但该模型参数较多,实际运用时计算量过大[16-17]。为此,研究者们采用类比的思想,建立了类似于衍生Maxwell及Kelvin模型的“先进”模型(适用于沥青的Huet 模型及适用于沥青混合料的Huet-Sayegh模型),仅需要6个模型参数即可达到8个Kelvin原件串联的拟合精度,但两个模型不能同时适用于沥青及沥青混合料[18-19]。Olard在Huet-Sayeah模型基础上进行了一定的改良,通过分析多种沥青及其沥青混合料在动态荷载下的力学响应关系,建立了同时适用于沥青及其混合料的先进“2S2P1D”模型[20]。
基于以上所述,本研究对沥青混合料进行短期和长期老化试验,并用单轴动态压缩模量试验测试了不同温度及频率作用下的动态模量,根据时温等效原理建立缩减频率与动态模量及相位角的关系,以2S2P1D模型为基础建立了动态模量主曲线,分析老化对沥青混合料的黏弹性能的影响,以期更好地了解老化过程中沥青路面的响应特征。
1 2S2P1D模型
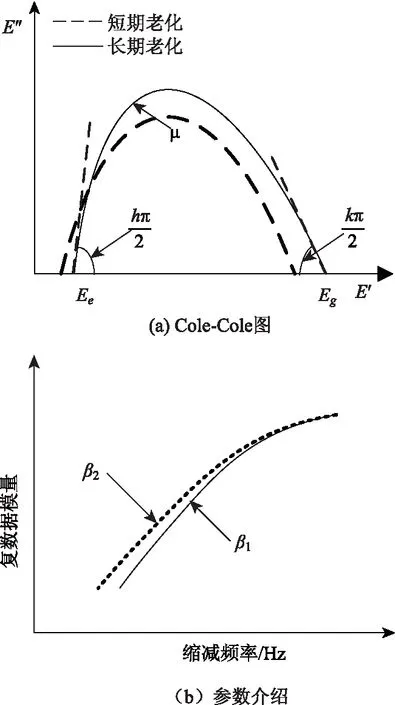
2S2P1D模型是一个由Huet-Sayegh模型衍生而来的一般化模型,由两个弹簧,两个抛物线蠕变元件和一个黏壶组合而成,能准确描述胶粘剂和沥青混合物的流变性质,如图2所示。根据Olard和Di Benedetto[20-22]的观点,抛物线单元是一个具有抛物线蠕变函数的类比模型,蠕变函数J(t)如式(1)所示:
(1)
复数模量方程如下所示:
(2)

图1 2S2P1D模型组成Fig.1 Composition of 2S2P1D model

(3)
2S2P1D模型由7个参数组成,而|E*|的表达式如式(4)所示:
(4)
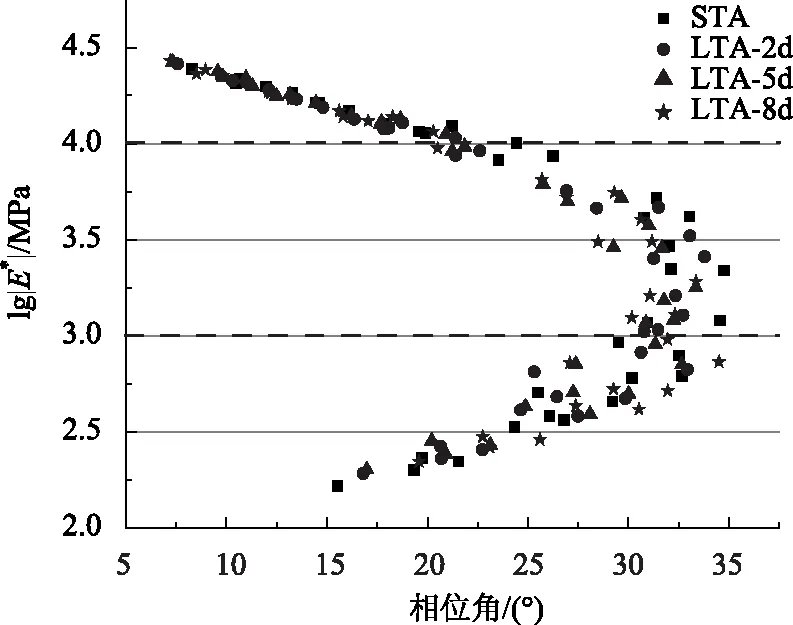
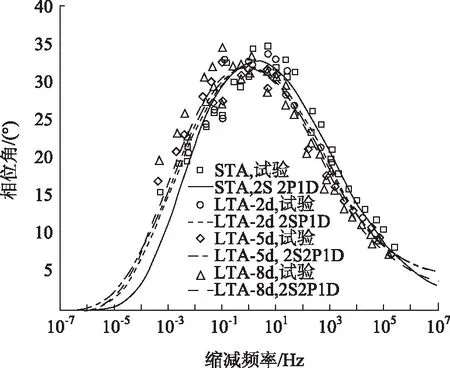
式中,k和h为一个与材料属性相关的指数,0 η=(Eg-E0)βτ, (5) 式中,η为牛顿黏度;τ为特征时间。该式与温度有关,在实验室测试的温度范围内可以通过诸如William, Landel and Ferry (WLF) 和 Arrhenius方程之类的移位因子法来近似演化: τ=aT(T)×τ0。 (6) 2S2P1D方程可以拆分成若干部分,重新写成如下形式[9]: (7) 式中, B(ω)=-(ωβτ)-1-μ(ωτ)-k× |E*|的虚部和实部可以分离如下: (8) 式中,E′=Eg-E0,DEN=(1+A(ω)2+B2(ω)。 必须强调的是,该模型只需要7个参数即可确定材料的流变性质。E0,Eg,k,h,μ和β分别在图2(a)和(b)中图解说明,表1详细地解释了k,h,μ和β等参数。 同时,相位角δ为: (9) 式中E′和E″是存储和损耗模量。 Di Benedetto等对9种粘合剂和4种沥青混合物进行的动态试验(采用一种混合物设计)发现该模型可以很好地拟合试验数据,即使在50°和70°之间的相位角仍然可以看到异常[20-21]。此外,该模型还被用于描述沥青胶浆的流变性质,并且k,h,α等参数对所有测试样品产生相同的值[22-23]。 表1 2S2P1D模型参数的意义Tab.1 Meanings of parameters of 2S2P1D model 图2 2S2P1D模型介绍Fig.2 Introduction of 2S2P1D model 目前我国高等级沥青路面的上面层几乎都采用改性沥青,因此本研究选择的沥青胶结料为SBS改性沥青(I-D),其基本性质如表2所示。集料选用玄武岩集料,基本性质如表3所示。 表2 SBS改性沥青基本性质Tab.2 Basic properties of SBS modified asphalt 表3 集料性质Tab.3 Properties of aggregate 混合料的级配采用密级配AC-13型,级配合成曲线如图3所示。 图3 沥青混合料级配曲线Fig.3 Aggregate gradation curves of asphalt pavement 沥青混合料采用旋转压实仪成型Φ150 mm×H170 mm,成型过程中采用控制箱压实次数制备4组平行试件,每组3个平行试件,共进行4种老化状态: (1)短期老化(STA):拌和后的松散混合料在强制通风的135 ℃烘箱中保温4 h,随后压实成型; (2)长期老化2 d(LTA-2 d):短期老化后压实成型的沥青混合料在强制通风的85 ℃烘箱中保温2 d; (3)长期老化5 d(LTA-5 d):短期老化后压实成型的沥青混合料在强制通风的85 ℃烘箱中保温5 d; (4)长期老化8 d(LTA-8 d):短期老化后压实成型的沥青混合料在强制通风的85 ℃烘箱中保温8 d。 在短期老化沥青混合料压实成型后,为模拟实际路面的长期老化状态,仅从上表面接触老化条件(空气、温度、阳光等),长期老化沥青混合料试件侧表面采用锡纸严密裹附,隔绝空气的进入,如图4所示。所有沥青混合料试件均在同一烘箱中完成老化。 图4 老化前的沥青混合料试件Fig.4 Samples of asphalt mixture before aging 对老化沥青混合料试件钻芯获取直径100 mm,高度150 mm的试件,利用单轴压缩动态模量试验测试试件的动态模量,为保证沥青混合料处于线性黏弹性范围内应控制试验过程中的应变小于100 με。试验温度选为0,4,15,30,45,60 ℃,试验频率为25,10,5,1,0.5,0.1 Hz。动态模量结果获得后,采用WTF公式进行时-温等效变换,运用MATLAB中的最小二乘法原理获取模型参数,从而建立良好的复数模量和相位角主曲线,参考温度选为30 ℃。缩减频率可通过时温移位因子计算获得,移位因子由式(10)~(11)计算获得: lgωr=lgω+lgα(T), (10) (11) 式中,ωr为缩减频率;T是试验温度;Tr是参考温度;C1和C2是模型参数,通过在MATLAB中编写程序拟合得到。 图5 不同老化状态下沥青混合料动态模量-相位角图Fig.5 Dynamic modulus vs. phase angle of asphalt mixture under different aging conditions Black diagrams of asphalt mixtures under different aging conditions SBS改性沥青混合料在不同老化状态下的动态模量Black diagrams如图5所示,结果表明随着SBS改性沥青混合料老化前后动态模量的减小,其相位角并不是越来越大,更无法趋近于90°,而是在某一动态模量时达到最大值。这意味着老化前后的SBS改性沥青混合料均表现出复杂的热流变行为,无法完全满足时温等效原理。然而,根据图6所示的基于WLF公式的时温等效变化,发现老化前后的沥青混合料动态模量主曲线是可以建立的,并对部分时温等效原理拟合度较高。同时从图5可以发现老化对动态模量及相位角的影响可以分为3部分,第1部分为动态模量大于10 000 MPa时(对应于试验温度小于15 ℃),不同老化状态下的模量基本贴近,但LTA-8 d的沥青混合料试件相位角最小而动态模量最大,STA动态模量最小而相位角最大,这是因为老化使得沥青混合料模量及弹性增强。第2部分为动态模量在1 000~10 000 MPa内,各不同老化状态下沥青混合料相位角及动态模量数据差异更为明显,但基本符合随着老化程度的增加,相位角不断减小而动态模量不断增大的关系。第3部分为模量小于1 000 MPa部分(对应于试验温度大于45 ℃),该部分动态模量仍然随着老化程度的增加而不断增大,但是相位角不再随着老化的增加而减小,出现这一现象的原因可能是温度较低时,混合料中沥青的弹性较强,对石料的摩阻力明显,荷载频率降低导致高分子链段的运动更为活跃,相位角增加;当试验温度升高时,混合料中沥青黏性增强,在高荷载频率下,高分子链段的运动勉强跟上外力的变化,因此相位角表现出波动,而随着频率的降低,滞后现象不明显,相位角减小;温度介于两者之间时,相位角随着频率的增加表现出先增加而后较小,而由于试验中使用的不同老化沥青混合料试件是同时老化,改变老化时间获得,并不是由一批老化沥青混合料先老化两天,待动态模量试验结束后再老化进行试验,因此,在不同的沥青混合料试件中,由于集料及沥青的不同空间分布特征,导致了高温试验中上述效应的不确定性,从而使得沥青混合料试件不再遵循老化时间越长,相位角越小的关系。 图6 STA沥青混合料时温等效变换示意(WLF公式)Fig.6 Illustration of time-temperature equivalent transformation of STA asphalt mixture (WLF formula) 各种老化状态下的沥青混合料模型拟合参数如表4所示。结果表明随着老化程度的增加,E0,k,h和τ0会不断较小,而Eg,μ及β会不断增大。Ee的略微减小是因为该参数对应于ω→0之时,沥青混合料中沥青对于动态模量的影响十分微小,而主要由石料骨架提供,故而在不同试件的情况下,E0变化与老化状态关联性较小。而Eg随着老化程度的增加而显著增加与沥青的贡献度有关,ω→∞之时,沥青硬化,老化会使得沥青黏度增大,因此老化后的沥青结合料对沥青混合料中集料的限制作用增强,造成模量显著增大。参数β亦验证了这一点,其在老化过程中也不断增大。k,h随着老化的减小而不断减小,体现在Cole-Cole图中为两端处的斜率不断减小,表明在老化后沥青的硬度增加导致沥青混合料的弹性增强。 表4 不同老化状态下沥青混合料模型拟合参数Tab.4 Fitting parameters of asphalt mixture model under different aging conditions 图7和图8为不同老化状态下沥青混合料动态模量及相位角主曲线,动态模量试验结果与2S2P1D模型拟合结果较好(相关系数大于0.98),但相位角主曲线则拟合结果较差(相关系数在0.9~0.95之间),根据线性相关系数的判别法则,2S2P1D能够完美地拟合动态模量,而仅能较好地拟合相位角主曲线[24],考虑到沥青混合料中沥青及集料对于相位角的贡献度的复杂性,这一结果是可以接受的。通过动态模量主曲线的放大图可以发现,在一定的频率范围内,老化会使得沥青混合料的模量增加,在频率非常小时,动态模量主曲线的差异将减小甚至可能出现不同老化状态的交叉,其与低频时沥青混合料中模量的贡献度有关,低频时沥青混合料中骨架结构对沥青混合料模量影响远远大于沥青胶结料的作用。而在相位角主曲线中,高频部分LTA2 d、LTA5 d及LTA-8 d的主曲线低于STA,但是到了低频部分,曲线出现了相反的情况,造成这种现象可能是因为低频时,沥青黏性对沥青混合料的黏弹特性作用不明显,因此老化对沥青黏性的增加作用不再模型,而沥青混合料骨架作用,需要后续通过试验对同一批试件进行不同老化状态的动态模量相位角主曲线进行验证。进一步地,本研究对STA及LTA-5 d的沥青混合料试件的储存模量(弹性部分)及损失模量(黏性部分)进行分析,结果如图9所示。该结果表明老化对沥青混合料模量的增加对储存模量及损失模量作用具有不同的规律,老化会增加中频范围内的储存模量,但频率极低时,老化基本没有影响。然而,在整个频率范围内,老化均会增加沥青混合料的损失模量,但随着频率趋近于0时,损失模量趋近于0。该结果与沥青混合料中胶结料及集料对沥青混合料的共享度有关,频率极低时(等价于高温),沥青的黏性对沥青混合料的黏弹性作用减弱;而当频率增加时,胶结料逐渐变硬,对集料限制作用增强,从而使得胶结料性质对混合料的影响增强。同时老化会增加沥青胶结料的黏度,增加其对集料的摩擦力,因此使得沥青混合料在老化过程中的动态模量增大。 图7 不同老化状态下沥青混合料动态模量主曲线Fig.7 Master curves of dynamic modulus of asphalt mixture under different aging conditions 图8 不同老化状态下沥青混合料相位角主曲线Fig.8 Master curves of phase angle of asphalt mixture under different aging conditions 图9 STA和LTA-5d的沥青混合料试件主曲线(30 ℃)Fig.9 Master curves of asphalt mixture specimens under STA and LTA-5d at 30 ℃ 通过对不同老化状态下的SBS改性沥青混合料进行多个频率及温度下的单轴动态模量试验,并基于2S2P1D模型分析老化对动态模量及相位角的影响,主要得到以下结论: (1)随着老化程度的增加,在低温及中温域的SBS改性沥青混合料动态模量不断增大而相位角不断减小,但是在高温域,由于沥青混合料的多相组成特点,相位角出现在同一温度下先随着频率增加后减小的规律。 (2)SBS改性沥青混合料不完全满足时温等效原理,但是可以在试验温度下采用部分时温等效原理对数据进行处理,从而建立基于2S2P1D模型的主曲线; (3)老化对于沥青混合料的2S2P1D模型中的Eg和β参数具有显著性的影响,老化程度的增加使其显著增大,这与沥青胶结料黏度增加具有一定的关联,黏度的增加进一步限制了石料间的相对运动,从而增加了沥青混合料的硬度及模量; (4)基于2S2P1D模型建立的动态模量及相位角主曲线与试验数据具有良好的拟合度,线性相关系数均大于0.9,而从动态模量及相位角主曲线可以看出,老化对于沥青混合料在不同频率域下具有不同的影响,频率趋近于0时,不同老化状态下的动态模量区别较小,主曲线存在一定的交叉,相位角甚至出现了短期老化最小,长期老化后增大; (5)基于2S2P1D模型建立的储存模量及损失模量主曲线表明,在低频时老化对于沥青混合料的黏弹性影响具有不同的规律,在频率趋近于0时,老化对储存模量的增强作用基本不存在,但是损失模量却随着老化程度的增加而显著增大。
2 试验原材料与方法
2.1 试验材料基本性质


2.2 级配设计

2.3 试件制备2.3.1 沥青混合料试件成型及老化

2.3.2 动态模量试验方法
3 试验结果与分析
3.1 基于2S2P1D沥青混合料动态模量主曲线建立

3.2 老化对沥青混合料主曲线影响分析



4 结论

