超临界CO2作用下煤体膨胀变形理论模型
孙可明,李天舒
(1.青岛理工大学 理学院,山东 青岛 266520; 2.辽宁工程技术大学 力学与工程学院,辽宁 阜新 123000)
超临界CO2的应用作为新兴绿色技术,在地下封存、混相驱油、钻井开采等方面受到广泛关注[1]。近年来,利用超临界CO2改善低渗透煤层渗透性从而提高煤层气采收率的方法已通过实验验证具有良好效果[2-4],但超临界CO2的注入将引起煤体膨胀变形,对储层渗透性的提高存在不利的影响[5-7]。针对注入CO2后煤体膨胀变形这一特殊的力学现象,国内外学者开展了大量的理论实验研究。张倍宁等[8]通过实验对CO2注入储层过程中煤体膨胀变形情况进行测量。WALKER等[9]利用实验研究发现CO2引起的煤体膨胀变形不是完全可逆的。对于吸附膨胀变形理论,PAN等[10]从热力学角度出发建立煤体吸附膨胀应变理论模型。周军平等[11]基于吸附过程中能量守恒原理和热动力学理论,建立煤岩吸附膨胀应变的理论模型。然而,目前对CO2作用下煤体膨胀变形规律的研究主要集中于非超临界状态。煤体吸附超临界CO2产生的吸附膨胀,在超临界温度下产生的热膨胀,在超临界孔隙压力作用下产生的基质变形都不同于非超临界状态,且超临界CO2具有似液非液、似气非气、对温压变化极敏感等特性。因此,超临界CO2对煤体膨胀变形的影响比非超临界状态复杂,研究超临界CO2作用下煤体膨胀变形理论模型至关重要。
传统的吸附理论通常认为吸附过程中最高平衡压力是吸附质的饱和蒸汽压,当平衡压力达到饱和蒸汽压时,气体将发生凝聚直至气体全部液化,然而超临界状态吸附质不能发生液化,不存在饱和蒸汽压的概念,超临界吸附是否和非超临界一样存在最高吸附平衡压力还存在争议。经典吸附理论多以绝对吸附量为基础建立,在非超临界状态下不对过剩吸附量和绝对吸附量进行区分,研究表明[12-13]超临界状态下的吸附等温线存在最大值,随着压力的增加等温线出现下降趋势,过剩吸附量与绝对吸附量的差值越来越大,因此不能套用经典吸附理论采用绝对吸附量对超临界状态进行研究。
综上所述,为解决采用绝对吸附量建立的传统吸附理论在超临界状态下不再适用的问题,运用过剩吸附量对超临界CO2作用下煤体吸附进行分析,且模型建立过程中,考虑孔隙压力和温度对煤体变形量的影响。
根据Elliott-Suresh-Donohue状态方程(ESD)及简化局部密度模型[14](SLD)确定超临界CO2作用下煤体吸附的过剩吸附量,基于热力学理论和吸附体系的内能关系得出煤体吸附超临界CO2产生的膨胀应变,且考虑超临界压力产生的压缩应变及超临界温度产生的热膨胀应变对煤体总体变形量的影响,最终得出超临界CO2作用下煤体膨胀变形模型。通过编程求解不同超临界温压条件下的煤体膨胀变形量并与试验结果对比分析验证,证明其合理性和适用性。
1 超临界CO2作用下煤体膨胀变形理论模型
1.1 主体相密度与逸度的确定
ESD方程是由不同加权形式的排斥力与吸引力组成的P-R状态方程[15],运用ESD状态方程对主体相密度进行求解:
Z=1+Zrep+Zattr
(1)
式中,Z为压缩因子;Zrep=4cη/(1-1.9η)为引力项压缩因子,c为排斥项形状因子η=bρ为无因次密度,b为方程参数,ρ为密度,kg/m3;Zattr=9.5qηY/(1+1.774 5ηY)为斥力项压缩因子,q为吸引项形状因子Y=exp(ε/kT)-1.061 7为引力项能量参数;ε为势能参数,kJ/mol;k为Boltzmann参数;T为温度,K。
对式(1)进行化简整理得

(2)
式中,P为压力,Pa;R=8.314为理想气体常数。
将温度与压力值代入式(2)整理化简,即可得出对应的主体相密度ρbulk。
ESD状态方程可以表示为逸度f对数形式表达式:

(3)
将求得的主体相密度ρbulk及对应温度T代入方程(3)可解出主体相逸度fbulk。
1.2 吸附相密度与逸度的确定
煤体作为非极性吸附剂,气固作用势φ(z)仅与CO2分子与煤体表面的距离有关。CO2分子与煤体表面的气固作用势可用Steele’s 10-4-3模型[16]计算:

(4)
式中,ρs为碳原子密度,nm-3;εsf为气固势能参数,kJ/mol;σsf为CO2分子与碳原子的碰撞半径,nm;Δ为相邻煤体分子层间距离,nm;z为CO2分子到煤体表面的距离,nm。
煤体微孔内相邻壁面的吸附势能会相互叠加,设煤体微孔平均宽度为H,气固作用势能φ(z)可以表示为
φ(z)=φ′(z)+φ′(H-z)
(5)
将式(4)代入式(5)即可求出CO2与煤体表面的气固作用势能φ(z)。
当吸附达到平衡时,主体相的化学势与吸附相的化学势相等,吸附相的化学势可以看作气体分子之间相互作用势与气固之间相互作用势的和:
μbulk=μff(z)+μfs(z)
(6)
式中,μbulk为主体相化学势,J/mol,μbulk(T)=μ0(T)+RTln(fbulk/f0);μff为气体分子之间相互作用势,J/mol,μff(z)=μ0(T)+RTln(fff(z)/f0);μfs为气固相互作用势,J/mol,μfs(z)=NAφ(z);μ0(T)为参考态的化学势,J/mol;NA=6.02×1023为Avogadro常数;f0为参考态逸度,Pa;fbulk为主体相逸度,Pa;fff(z)为z点处吸附相逸度,Pa。
对式(6)进行化简整理,得出吸附相中任意点z处的逸度:

(7)
将求得的主体相逸度fbulk、气固作用势φ(z)及对应的参数代入式(7)即可求得z点处吸附相的逸度fff(z)。
CO2在整体上可视为非均相流体吸附质,在距离煤体表面z点处可近似为密度ρ(z)的局部均相流体,将ESD状态方程运用到吸附相时必须对方程中表示分子之间相互吸引作用的参数进行修正。被吸附的CO2分子靠近煤体孔壁的内表面,因此分子间的引力势能与微孔的几何形状以及分子在孔内的位置有关[17],通过位形积分可以得到修正后的吸附相引力项能量参数Y(z):
0.186≤z<0.558

(8)
H-0.898≤z 将修正后的引力项能量参数Y(z)代入ESD状态方程的逸度对数形式表达式(3),可得出吸附相的密度ρ(z)。 SLD模型是将吸附剂简化成狭缝模型,由于相互作用势能的存在,使狭缝内吸附的分子排列不均匀,通过确定狭缝内的密度分布,并根据简化的Simpson规则对狭缝吸附相与主体相密度差值积分来确定过剩吸附量。因此采用SLD模型对煤体吸附超临界CO2进行分析。 将求得的主体相密度ρbulk及吸附相密度ρ(z)代入SLD模型,得出过剩吸附量n: (9) 其中,S为吸附剂的比表面积,m2/g;H为微孔的平均宽度,nm。如:S=70 m2,ε/k=104 K,P=1.0 MPa,当H=1.35 nm,n=5.47 mmol/g;H=1.50 nm,n=5.62 mmol/g,因此理论上微孔平均宽度H越大,过剩吸附量n越大。 基于热力学理论[18],多微孔吸附剂与吸附质所组成的吸附体系的内能为 (10) 式中,U为比内能,J/kg;T为温度,K;S′为系统熵,J/(kg·K);V为比容,m3/kg;μ为化学势,J/kg;m为吸附剂的质量,kg。 当吸附达到平衡后,根据吸附体系中吸附质与吸附剂的内能关系可以得出 Ua=U-Us (11) Sa=S′-S′a (12) Va=V-Vs (13) (14) Us=TSs-PVs+μsm (15) (16) 式中,Φ=μ-μs为单位质量吸附剂发生吸附引起的表面能改变量,J/kg;上角标a表示吸附相状态;上角标s表示主体相状态。 基于Gibbs界面假设及吸附体系的内能关系[10,19]可以得出吸附相的表面自由能: (17) dGa=dUa+PdVa+VadP-TdSa-SadT= (18) (19) 整理得 (20) (21) 等温吸附过程中,假设煤体为各向同性弹性体,不考虑压力对煤体造成压缩变形影响,由于弹性能改变量等于表面能改变量,吸附膨胀应变可表示为 (22) f(x,νs)= (23) 式中,εs为煤体吸附膨胀产生的体积应变;γ=Φ/A为比表面能,J/(kg·m2);A为比表面积,m2/kg;Es为固体相弹性模量,Pa;f(x,νs)为与主体相泊松比相关的逸度,Pa;νs为主体相泊松比;c=1.2;x为煤体微孔半径与长度的比。 煤体作为主体相时其泊松比无法直接测量,基于Bentz[20]建立的由任意不重叠放置球形孔所组成的多孔固体中ν与νs的关系式可以得出 (24) 其中,ν为煤体泊松比;νs为煤体作为主体相时其泊松比;φ为煤体作为主体相时孔隙渗透率。将式(22)~(24)联立即可求出煤体吸附超临界CO2产生的膨胀应变εs。 超临界CO2作用下煤体膨胀应变不仅由吸附CO2产生,煤体在超临界温度下将产生热膨胀,在超临界孔隙压力作用下将产生基质变形,因此超临界CO2作用下煤体膨胀应变是煤体吸附超临界CO2产生的吸附膨胀应变、超临界压力产生的压应变及超临界温度产生的热膨胀应变共同组成的。 利用煤体对氦气难以吸附,不能产生吸附膨胀变形的特性,确定孔隙压力引起煤体的变形。根据体积应变Hooke定律可得出超临界孔隙压力产生的体积应变: (25) 式中,εp为体积应变;K=Es/[3(1-2ν)]为体积膨胀模量。 在煤体处于无应力状态及各向同性的假设下,煤体的温度由T0上升到T将会产生热膨胀应变: (26) 式中,εT为热膨胀应变;β为热膨胀系数。 超临界CO2作用下煤体膨胀应变ε表示为 ε=εs+εP+εT (27) 为分析超临界CO2作用下煤体膨胀变形规律,采用自主研发的膨胀变形测试装置,利用ISCO高压无脉冲计量双泵的恒压模式对煤体膨胀变形量进行测量。试验装置有效地弥补了传统膨胀变形试验用应变片采集变形数据时只能进行点测量、测量范围小、试验结果离散性大、超临界CO2作用下应变片与煤体试件易脱离破损等不足。 对超临界CO2作用下煤体体积应变进行测量,在施加恒定孔隙压和轴压的情况下,煤体膨胀变形将引起围压改变,为保持围压稳定,计量泵内流量值将随之发生改变,因此计量泵内流量的改变即可真实准确地反映煤体的体积变形量。体积应变测量原理,如图1所示。 图1 煤体膨胀体积应变测量原理Fig.1 Measuring principle diagram of coal swelling volumetric strain 当温度高于临界温度(31.1 ℃)、压力超过临界压力(7.38 MPa)时,CO2进入超临界状态。试验采用恒温水浴系统可以安全有效地确保试验温度的恒定,并采用孔压控制系统为试验提供恒定的孔隙压力,保证试验过程中煤体试件始终精准恒定的处于同一温压条件的超临界CO2作用环境。通过加载系统对试验测量时的煤体试件施加载荷,可以更好地反映实际储层地应力条件对膨胀变形规律的影响。煤体膨胀变形测量装置包括[21]:由压力泵、空气压缩泵、高压CO2气瓶、压力釜等组成的注气注水加载系统;三轴压力室;水浴恒温系统;由电磁阀、增压泵、数据记录仪等组成的孔压控制系统;由ISCO 高压无脉冲计量双泵、数据记录仪组成的数据测量采集系统等试验仪器,试验装置示意,如图2所示。 图2 试验装置示意Fig.2 Sketch of experimental equipment 由于原生结构煤的非均质和各向异性,导致多个试件实验时其结果难以区分是煤结构差异还是由温度及压力变化产生的膨胀效应。为便于实验结果对比分析,将原煤粉碎筛分,制作粒径相近的型煤可近似为各向同性体型煤作为试验试件。吸附平衡时间为24 h。试验步骤如下: (1)密封试件,按照图2所示连接试验仪器并检查各接口密闭性,确保试验装置正常工作; (2)向三轴压力室施加荷载,通过压力控制阀使轴压和围压匀速地达到预定压力值; (3)对试件进行抽真空并打开排气阀排气,排除型煤试件孔隙内残留空气,保证煤体孔隙内都充满超临界CO2; (4)将ISCO高压无脉冲计量双泵设为恒压模式,通过伺服加载系统和孔压控制系统对型煤试件施加预定的孔隙压力,并确保孔隙压力值稳定; (5)将三轴压力室静置于预定温度的恒温水浴内,使煤体充分完成因受热产生的膨胀变形; (6)记录ISCO高压无脉冲计量双泵流量值随时间变化情况,流量值不再改变后停止试验。 改变试验温压条件,重复试验步骤(2)~(6),测定不同温压情况下煤体的膨胀体积应变,各组试验温压值见表1。 表1 温压参数 试件温度/K围压/MPa轴压/MPa孔隙压力/MPa1308.158.58.08.02313.158.58.08.03318.158.58.08.04323.158.58.08.05313.158.07.57.56313.159.08.58.57313.159.59.09.0 按照表1的温压状态,对超临界CO2作用下煤体体积应变进行测量,试验结果见表2。 表2 不同温压条件下煤体膨胀体积应变量试验值 试件编号温度/K孔隙压力/MPa试验体积应变1308.158.00.017 752313.158.00.069 123318.158.00.143 884323.158.00.157 645313.157.50.039 586313.158.50.180 377313.159.00.188 47 为了验证膨胀变形理论模型的适用性和准确性,利用Matlab软件对超临界CO2作用下煤体膨胀变形理论模型进行编程计算,并将理论模型计算值与试验数据进行对比分析。 CO2的ESD状态方程参数见表3,CO2分子与煤体表面的气固作用势参数见表4。 表3 CO2的ESD状态方程参数 排斥项形状因子c吸引项形状因子q方程参数(ε/k)/K方程参数b/(m3·mol-1)1.832 12.585178.2691.053 4×10-5 表4 CO2分子与煤体表面气固作用势参数 碳原子密度ρs/nm-3气固势能参数εfs/(kJ·mol-1)碰撞半径σsf/nm相邻煤分子层间距Δ/nm11414.20.3560.335 为便于理论模型数据与试验数据的对比分析,理论模型中煤样参数选取试验采用的自制型煤的相关参数,见表5。 表5 固体相煤体的相关参数 微孔平均宽度H/nm比表面积S/(m2·g-1)弹性模量Es/MPa泊松比ν热膨胀系数β/(m·℃-1)1.5702 3000.326.435×10-6 不同温压条件的超临界CO2作用下煤体膨胀体积应变的理论模型计算值,见表6。 将通过理论模型计算得出的膨胀体积应变与试验测量的膨胀体积应变进行对比分析。 图3(a)为超临界孔隙压力P=8.0 MPa时,不同超临界温度作用下,试验测量得出体积应变数据与理论模型计算得出体积应变数据的对比图。图3(b)为超临界温度T=313.15 K时,不同超临界孔隙压力作用下,试验测量得出体积应变数据与理论模型计算得出体积应变数据的对比图。 由图表分析得出,建立的超临界CO2作用下煤体膨胀理论模型计算数据与试验数据基本吻合,理论模型能较好地体现超临界CO2作用下煤体膨胀变形情况。可以有效地反映不同温压条件的超临界CO2作用下煤体膨胀变形规律。超临界CO2作用过程中,煤体体积应变随超临界温度和超临界孔隙压力均呈“S型”Logistic函数规律变化。 表6 不同温压条件下煤体膨胀体积应变理论值 温度/K孔隙压力/MPa吸附膨胀应变孔压压缩应变热膨胀应变理论体积应变303.158.000.029 941-0.001 2520.000 0210.028 71308.158.000.054 860-0.001 2520.000 0320.053 64310.658.000.075 585-0.001 2520.000 0370.074 37313.158.000.106 039-0.001 2520.000 0430.104 83315.658.000.133 654-0.001 2520.000 0480.132 45318.158.000.138 439-0.001 2520.000 0530.137 24320.658.000.142 873-0.001 2520.000 0590.141 68323.158.000.144 038-0.001 2520.000 0640.142 85325.658.000.154 472-0.001 2520.000 0700.153 29330.658.000.158 592-0.001 2520.000 0800.157 42313.157.500.053 841-0.001 1740.000 0430.052 71313.157.750.065 540-0.001 2130.000 0430.064 37313.158.250.138 928-0.001 2910.000 0430.137 68313.158.500.199 638-0.001 3300.000 0430.198 35313.158.750.214 937-0.001 3700.000 0430.213 61313.159.000.223 396-0.001 4090.000 0430.222 03313.159.250.220 295-0.001 4480.000 0430.218 89313.159.500.224 294-0.001 4870.000 0430.222 85 图3 体积应变随超临界温度和超临界孔隙压力变化曲线Fig.3 Curves of volumetric strain changes with the supercritical temperature and the supercritical pore pressure conditions 目前各种测量吸附的方法都是对过剩吸附量的测量,绝对吸附量无法通过实验方法进行测定,而传统吸附理论都是建立在绝对吸附量的基础上,且超临界状态下绝对吸附量与过剩吸附量的差值增大。运用简化局部密度模型直接确定过剩吸附量并求解吸附膨胀变形,可以更好地反映超临界状态下吸附情况。建立的理论模型能较好地体现超临界CO2作用下煤体膨胀变形情况,可以有效地反映不同温压条件的超临界CO2作用下煤体膨胀变形规律。 模型建立的过程中,对部分情况进行了假设和简化。理论模型在确定过剩吸附量的过程中,型煤试件吸附过程的渗透率变化并未考虑,渗透率变化引起的煤体孔隙平均宽度的变化也未考虑。此外,影响微孔平均宽度的因素较多,在超临界CO2作用下煤体膨胀变形理论模型中,温度和压力变量作为考虑的主要影响因素,微孔平均宽度采用一个固定值进行计算,并未考虑微孔宽度变化对膨胀的影响,考虑不同微孔宽度的型煤吸附实验需要进一步研究。采用SLD理论将吸附剂简化成狭缝模型,并根据简化Simpson规则对狭缝吸附相与主体相密度差值积分确定过剩吸附量,同时为便于实验结果对比分析,将原煤粉碎筛分,制作粒径相近的型煤可近似为各向同性体,然而实际的煤体孔隙结构比较复杂,如何更好地反映吸附剂孔隙结构仍需进一步研究。分析超临界CO2作用下温度对煤体膨胀变形的影响,实验测获得了温度应力引起的热膨胀应变,但吸附膨胀应变是通过吸附量及表面自由能得出的,非等温吸附其同时受温度和压力影响,实验数据采集没有单独分离温度和压力分别对吸附膨胀的信息,仍需进行后续的研究。 (1)为分析超临界CO2作用下煤体膨胀变形规律,解决采用绝对吸附量建立的经典吸附理论在超临界状态下不再适用、超临界CO2作用下煤体变形除吸附外还需考虑孔隙压力及温度对变形的影响等问题,建立超临界CO2作用下煤体膨胀变形理论模型。 (2)根据ESD状态方程及SLD模型求出超临界CO2作用下煤体的过剩吸附量,基于热力学理论和吸附体系内能关系确定煤体吸附超临界CO2产生的膨胀应变,并考虑超临界压力产生的压应变及超临界温度产生的热膨胀应变,最终建立超临界CO2作用下煤体膨胀变形理论模型。 (3)通过编程计算对建立的理论模型进行编程计算数值解,并与通过自主研发的具有施加热流力载荷功能的膨胀体积应变测量装置的测量结果进行了对比分析。理论模型计算数据与试验测量数据吻合度较高,可以有效地反映不同温压条件的超临界状态CO2作用下煤体膨胀变形情况。 (4)超临界CO2作用过程中,煤体体积应变随超临界温度和超临界孔隙压力均呈“S型”Logistic函数规律变化。在利用超临界二氧化碳提高煤层渗透性时,根据曲线选择合适的超临界温压条件,避免煤体膨胀对渗透性的不利影响。1.3 过剩吸附量的确定

1.4 吸附应变的确定

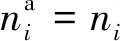



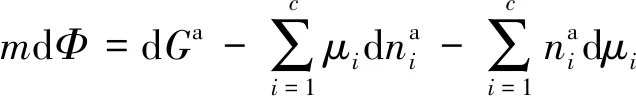
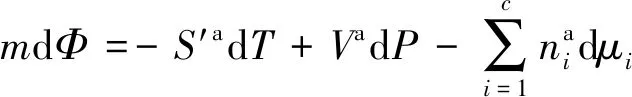




1.5 超临界CO2作用下煤体膨胀应变的确定
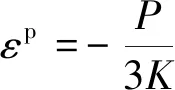
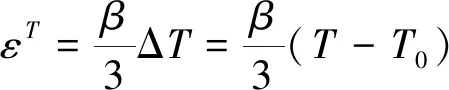
2 模型验证
2.1 煤体膨胀应变试验
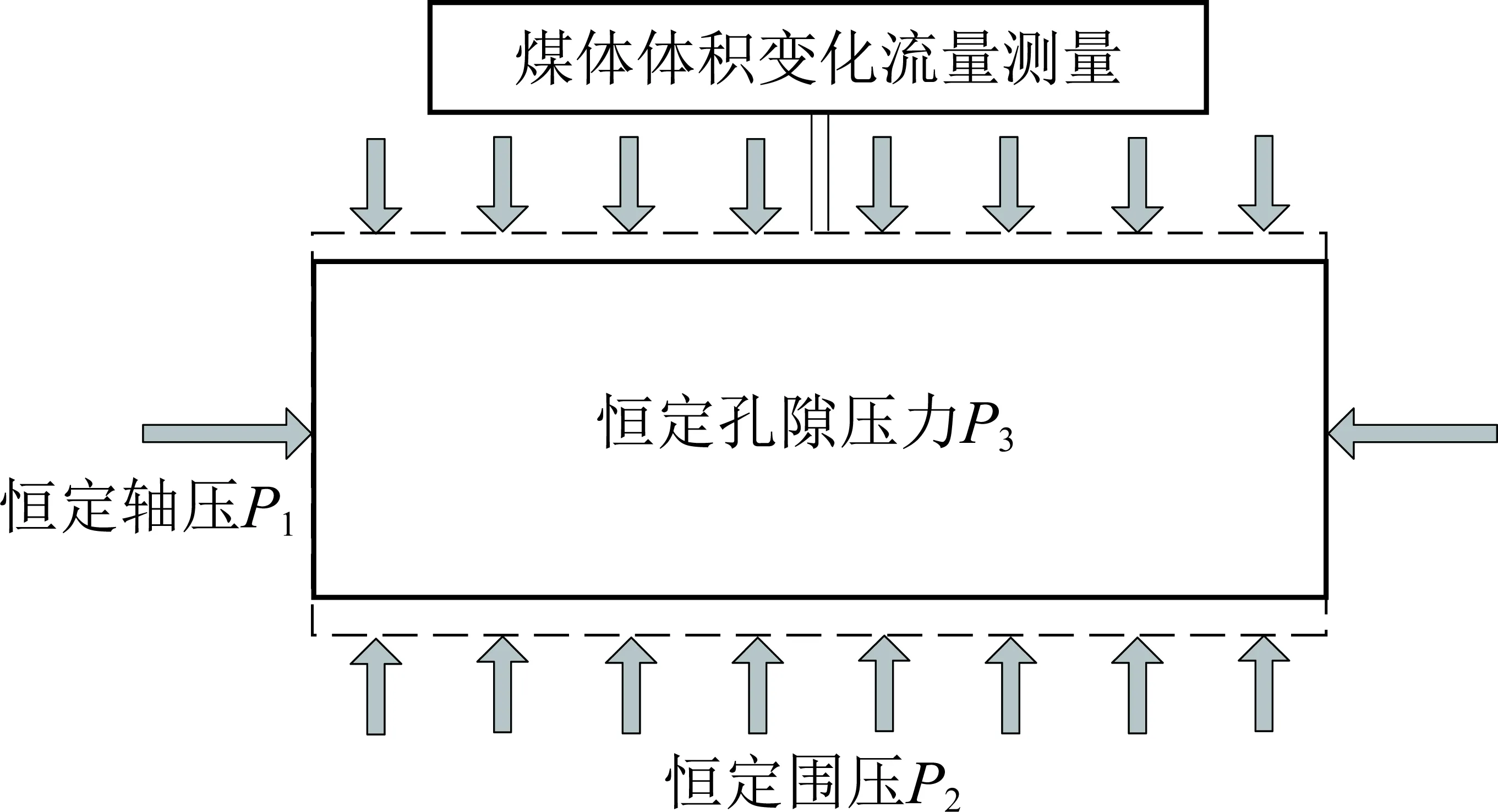
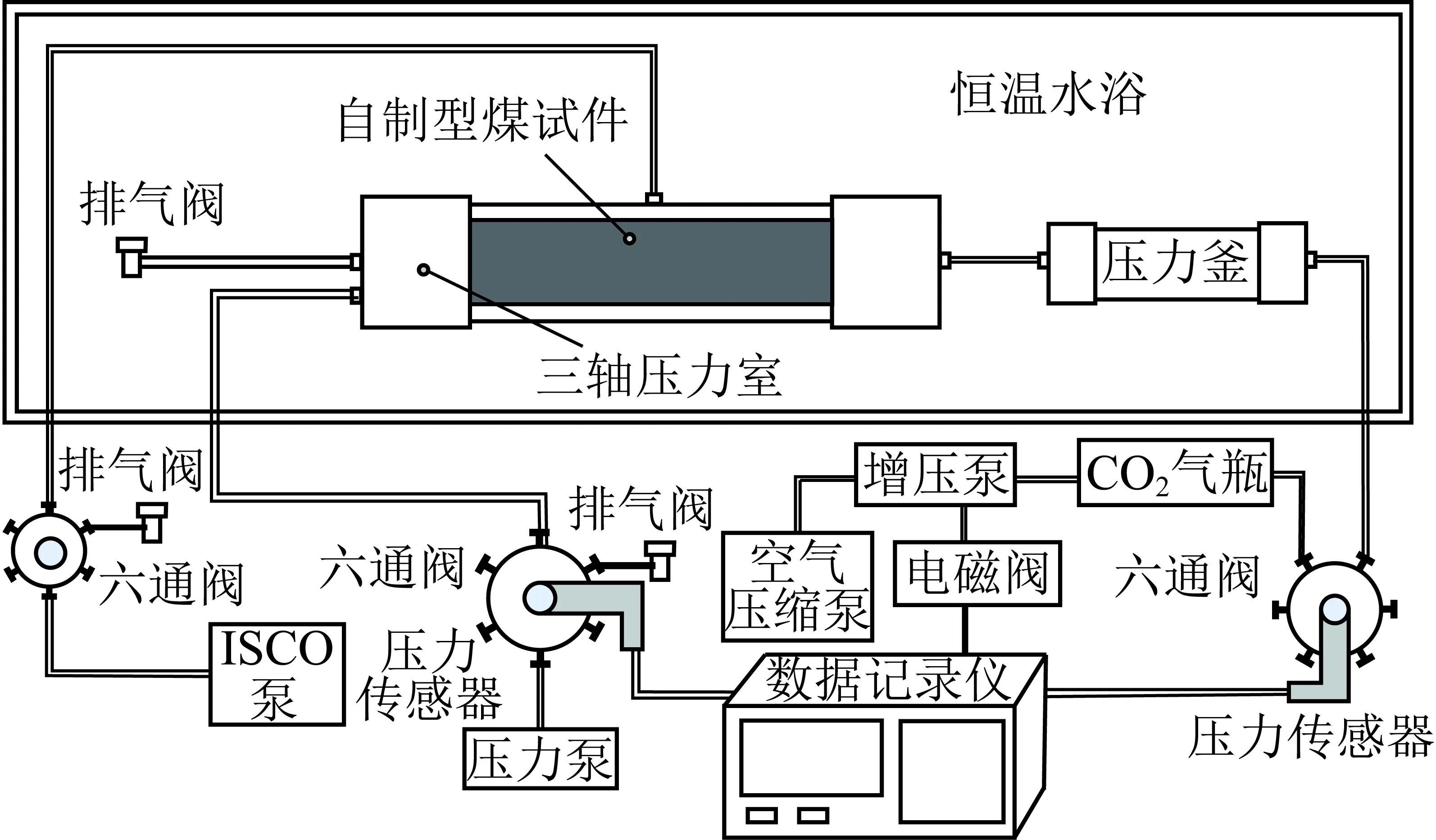
Table 1 Parameter list of temperature and pressure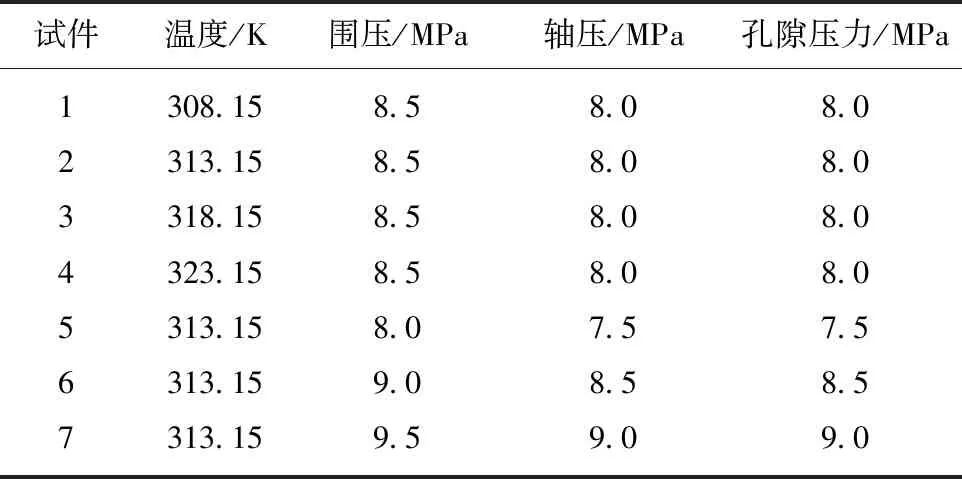
Table 2 Volumetric strain of coal swelling under different temperature pressure conditions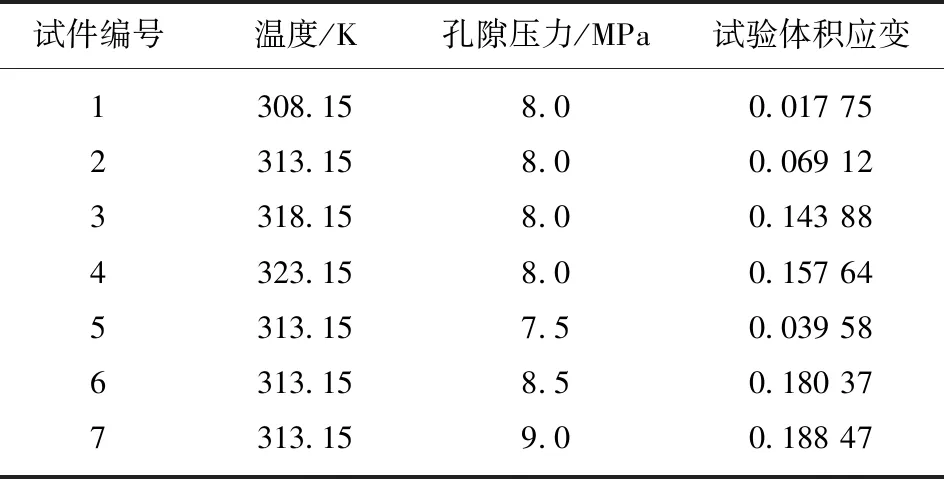
2.2 煤体膨胀应变理论模型计算
Table 3 ESD state equation parameters of CO2
Table 4 Potential energy parameters of CO2molecules and coal surface gas-solid interaction
Table 5 Parameters of solid phase coal
2.3 对比分析
Table 6 Volumetric strain of coal swelling under different temperature pressure condition

2.4 讨论及误差分析
3 结 论

