软岩现场流变试验及非线性分数阶蠕变模型

刘泉声，罗慈友，彭星新，刘 鹤，陈 磊，潘玉丛

(1.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071; 2.武汉大学 岩土与结构工程安全湖北重点实验室，湖北 武汉 430072; 3.中国科学院大学，北京 100049; 4.中铁十一局集团第四工程有限公司，湖北 武汉 430073)

随着浅部资源的逐渐枯竭，矿产资源开采深度逐年增加[1-2]。随着开采深度的增加，软岩矿井的数量不断增大，软岩相关的工程问题也不断加剧，其中因软岩的流变导致的工程稳定性问题日益凸显[3]，有必要对软弱岩体的流变特性展开深入的研究。

许多学者进行了软岩流变特性相关的研究工作。岩石室内流变试验是获取其流变力学性质的主要手段[4-9]，因为相对于现场实测，它具有可重复次数多、试验条件可控制性好、易排除次要影响因素和试验成本低等优点。然而对于工程岩体，其含有大量结构面，且存在尺寸效应[10]，室内标准的流变试验结果难以准确反映其流变力学特性。现场岩石流变力学试验由于需人力物力投入大、技术难度大和试验周期长等原因，目前仅开展了为数不多的相关试验研究[11]。中国电建集团成都勘测设计研究院有限公司对二滩水电站坝基蚀变玄武岩进行了现场柔性承压板岩体压缩蠕变试验[11]。吴玉山等[12]对某矿的松散块状二辉橄榄岩进行了刚性垫板流变试验，采用三参量固体模型进行了岩体参数的确定。KORZENIOWSKI[13]进行了煤矿坚硬煤柱的现场单轴压缩蠕变试验，采用Burgers模型进行了岩体流变参数的计算。徐平等[14]对溪洛渡水电站坝址区岩体进行了柔性板无中心孔法压缩蠕变试验，并采用三参量固体模型进行了参数反演。贺如平、张强勇等[15-16]进行了大岗山水电站坝区辉绿岩脉大型刚性承压板压缩蠕变试验，并分别采用经验方程和三参量固体模型进行了岩体流变参数的回归拟合。龚成等[17]进行了锦屏水电站左岸边坡砂板岩松弛岩体的承压板原位蠕变试验，并分别采用三参量固体模型和Burgers模型进行了岩体参数的反演。陈卫忠等[18]进行了国投新集刘庄煤矿回风巷底板软岩的现场三轴流变试验，并采用非线性幂函数蠕变模型拟合获得了泥岩流变力学参数。可见，现场岩体流变试验研究虽然取得了一定的成果，但目前国内外开展的还是较少，对于具体工程问题，如果条件允许还是有必要展开相关的研究工作。

对于岩石流变本构模型问题的研究，国内外成果卓著，其中岩石的非线性粘弹塑性流变本构模型研究是热点之一。徐卫亚等[19-20]基于岩石的非线性加速蠕变特征，提出了NVPB元件，并与五元件模型串联，建立了河海模型。夏才初等[21-22]建立了包含15个流变力学模型的统一流变模型，并介绍了采用该统一流变模型理论确定流变模型和参数的方法。STEIPI等[23]认为西原模型中的黏塑性参数为黏塑性应变的线性函数，并据此改进了西原模型。陈卫忠等[24-25]提出了泥岩的非线性经验幂函数蠕变模型和辉绿岩脉的非线性损伤粘弹塑性本构模型。张强勇等[26]基于岩体流变过程中的损伤劣化效应，提出了变参数的蠕变损伤模型。此外，还有许多其他理论研究成果难以一一介绍[27-29]。可以看出，目前岩石流变本构模型的研究重点主要为针对一些具体问题对以往模型的改进以及非线性流变本构方程的研究。

另外，近年来有学者尝试将分数阶微积分理论应用于岩石的流变本构模型研究。分数阶微积分理论是研究任意阶微积分的理论，其中分数阶导数近年来被越来越多地应用于描述各类复杂的力学与物理行为[30]。材料的应变状态与其所受的整个应力历史有关，而分数阶时间导数正是微分-积分卷积算子，充分体现了系统函数发展的历史依赖性[31]，因此可用于描述岩土体的蠕变变形规律。殷德顺等[32]利用Riemann-Liouville的分数阶微积分算子及理论，通过软体元件与弹簧元件串联或并联，建立了土体的流变模型;H.W.ZHOU等[30,33]通过将分数阶Abel黏壶代替西原模型中的Newton黏壶的方法，建立了岩盐的分数阶流变模型;吴斐等[34]在H.W.ZHOU等的研究基础上，采用Abel黏壶替代后者提出的模型中的Kelvin体，并认为模型中前后2个Abel黏壶的求导阶数不同，建立了新的分数阶粘弹性蠕变模型;丁靖洋等[35-36]引入损伤和分数阶微积分理论，分别建立了岩盐的分数阶三元件模型和改进的西原模型。以上将分数阶微积分理论应用于岩石流变本构模型的研究主要有采用Abel黏壶代替Newton黏壶和Kelvin体两种，都取得了较好的效果。

为研究现场软弱岩体的流变力学特性，本文拟开展煤矿巷道底板大体积软弱岩体的现场压缩蠕变试验，根据试验结果并结合分数阶微积分理论建立现场软弱岩体的流变本构模型，最后反演获得流变力学参数，以求为相关理论及工程研究提供参考。

1 软弱岩体现场流变试验

由于难以将现场大体积软弱岩体完好地采集、运输和搬运至室内进行加工及试验，拟采用在煤矿井下巷道底板现场制备立方体岩体试样，并安装上自行研制的现场岩体流变试验设备，最后进行大体积岩体试样的现场分级加载蠕变试验。

1.1 岩体试样制作

试样分别选自平顶山市平煤八矿装载硐室回风道和风巷设备道底板岩层，两处巷道底板埋深分别为-691.7 m和-708.5 m。已有文献[37]表明，平煤八矿地应力分布具有一定的规律:有两个主应力接近于水平方向，另一个主应力接近于垂直方向。最大主应力位于近水平方向，大小为自重应力的1.9～2.2倍，垂直应力值基本等于或稍大于单位面积上覆岩层的自重，大小为自重应力的0.93～1.12倍。根据测点埋深及文献[37]中关于平煤八矿地应力值随深度变化的经验方程可计算得知两测试地点地应力值见表1。

表1 平煤八矿测点处地应力大小
Table 1 Ground stress at the measuring point of Pingdingshan No.8 Mine

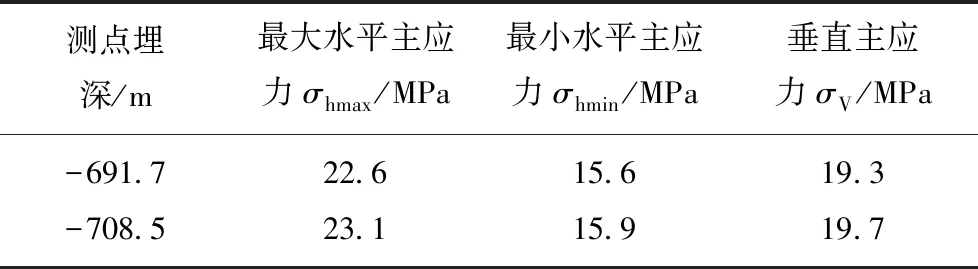
测点埋深/m最大水平主应力σhmax/MPa最小水平主应力σhmin/MPa垂直主应力σV/MPa-691.722.615.619.3-708.523.115.919.7

试验地点岩石为微风化较坚硬砂岩，岩体强度较弱，完整性较差，为块状结构，有较为发育的节理裂隙和层面，主要结构面张开度小于1 mm，结构面平直，结合一般，各节理裂隙长度约100～200 mm，综合判断属于Ⅳ类围岩，具有一定的代表性。

设计岩体试样最终成型尺寸为730 mm×730 mm×780 mm，岩体试样及试验基坑示意如图1所示。具体制作过程:① 清除试验区域底板表层约300 mm厚的破碎浮渣，确保岩体试样是原样岩体;② 以岩体试样表面中心为中心，采用风钻开挖出外边界3 030 mm×3 030 mm、内边界930 mm×930 mm、深度780 mm的“回”字型基坑，形成岩体试样毛坯及试验基坑;③ 用手锤和凿子对岩体试样毛坯做精凿处理，使之尺寸接近730 mm×730 mm×780 mm，并采用M25水泥砂浆对岩体试样上表面进行抹平处理。

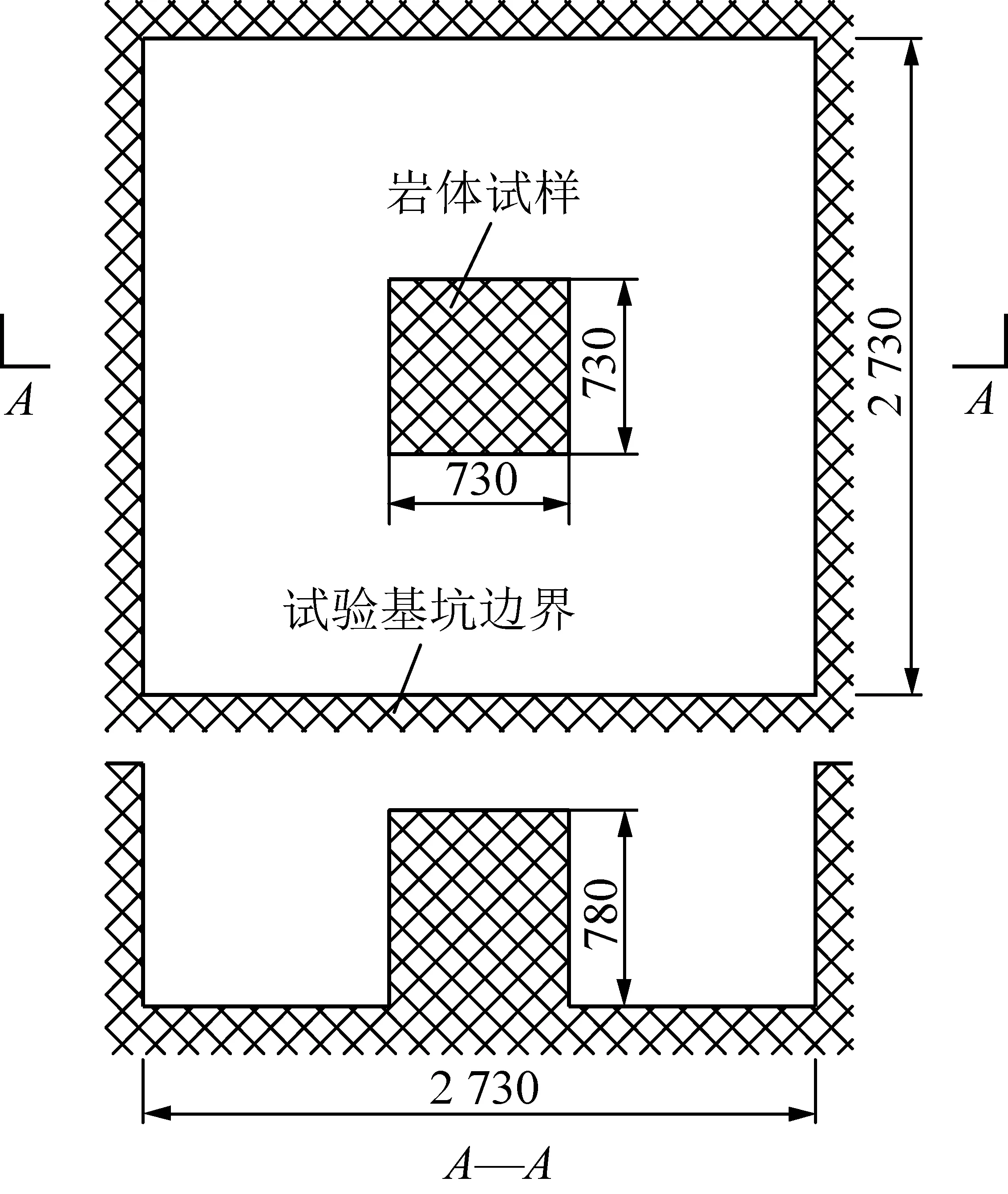
图1 岩体试样及试验基坑示意Fig.1 Schematic diagram of rock mass specimen and test foundation pit

1.2 试验仪器安装

采用中国科学院武汉岩土力学研究所自行研制的现场岩体流变试验设备[38]进行试验。该设备主要由3部分组成:

(1)加压稳压系统。包括轴向加压稳压系统和侧向加压稳压系统。轴向可提供最大荷载为15 000 kN，对于730 mm×730 mm×780 mm的岩体试样的轴向最大理论加载应力可达30.6 MPa;侧向可提供最大荷载为5 000 kN，对于730 mm×730 mm×780 mm的岩体试样的侧向最大理论加载应力可达9.5 MPa。

(2)变形测量系统。岩体试样的变形测量系统包括轴向位移测量部分和侧向位移测量部分。采用百分表进行位移测量，配合磁力表座和固定桩等支撑和固定装置。岩体试样轴向变形的测量，考虑到在轴向荷载下岩体试样会出现整体下沉，通过测量岩体试样顶部的绝对下沉量和底部的绝对下沉量，计算顶部下沉量和底部下沉量的差值来获得岩体试样的轴向变形量。为减小测量误差，岩体试样顶部和底部各布置4套磁力表座和百分表，顶部和底部各4个百分表的变形量的平均值即分别为岩体试样顶部和底部的绝对位移值。8套位移测量装置均分别固定于埋设在试验基坑内地板上的4个固定桩上，各固定桩均埋设于岩体试样外围一定距离的巷道底板上，以降低岩体试样变形对固定桩的扰动影响。

(3)整体框架。整体框架包括整套设备的各部分传力装置，实现荷载的传递及对适宜尺寸的岩体试样的均匀接触和加载。

采用该套设备进行岩体试样的单轴分级加载蠕变试验。试验现场安装图如图2所示。

图2 试验现场安装Fig.2 Installation of in-situ tests

1.3 加载方案设计

岩石流变试验按加载方式的不同，可分为多试样单级加载和单试样分级加载两种方式，鉴于现场岩体试样的难以制备以及单试样逐级增量加载法可避免不同试样导致试验结果离散性的缺陷，本次试验采用单轴分级加载的加载方式进行。考虑试验现场岩体力学特征，岩体试样加载方式如下:

(1)以0.05 MP/s的加载速率加载至σ1，保持轴压不变，每0.5 h或1 h记录一次岩体试样的轴向变形随时间的变化;

(2)以1.25 MPa的大小逐级增加轴向荷载，保持轴压不变，每0.5 h或1 h记录一次岩体试样轴向变形随时间的变化，直至岩体试样变形速率趋于稳定或迅速发生加速蠕变破坏;

(3)如果岩体试样发生加速蠕变破坏，则试验停止。

由于试验地点位于轨道大巷附近，距离掘进及采煤工作面都较远，环境较为稳定，试验过程不受工作面的振动等影响。且由于是进风大巷，巷道内为新鲜空气，试验过程中温度与湿度变化范围不大。

1.4 蠕变试验结果

按照设计的加载方案对岩体试样进行分级加载蠕变试验，直至应力水平达到8.75 MPa，加载约20 h后岩体试样发生破裂破坏，产生了近轴向宏观破坏面及侧角脱落现象。平顶山市平煤八矿巷道底板软弱岩体试样典型分级加载蠕变曲线如图3所示。

图3 试样单轴流变全程曲线Fig.3 Complete curve of rock creep under uniaxial rheological tests

对分级加载蠕变试验数据进行处理，获得各级应力水平下岩体试样的蠕变曲线及蠕变速率曲线。岩体试样各级应力蠕变和蠕变速率曲线如图4所示。

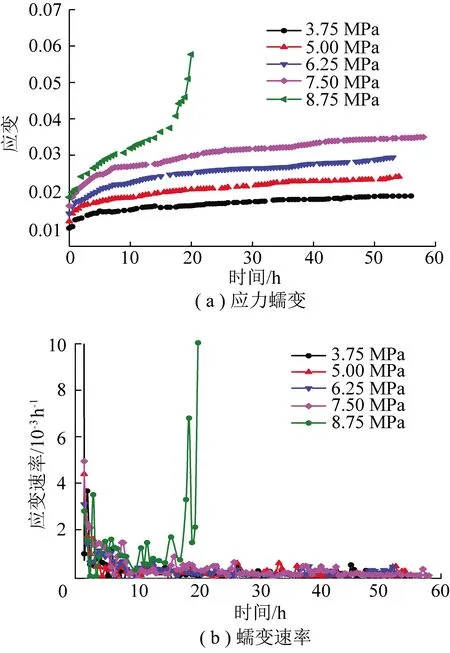
图4 岩体试样各级应力蠕变和蠕变速率曲线Fig.4 Creep curves and creep rate curves of rock mass samples under different level of stress

由图4可见，在本次蠕变试验中，岩体试样在应力水平为3.75,5.00,6.25和7.50 MPa时都是先经历衰减蠕变阶段，10～20 h后基本进入稳定蠕变阶段，直至约60 h时而并未出现明显的加速蠕变特征;而当应力水平达到8.75 MPa时，岩体试样在经历较短时间的衰减蠕变阶段、稳定蠕变阶段后，于约15 h后便很快显现出加速蠕变特征，并迅速发生破坏。

根据张治亮和徐卫亚等[39]的观点，可将发生加速蠕变破坏的前一级应力近似地认为是加速蠕变应力阈值σs，即当应力水平超过加速蠕变应力阈值σs后，岩样将迅速发生加速蠕变并最终破坏。据此，本文可将7.50 MPa确定为岩体试样的加速蠕变应力阈值。

2 非线性分数阶蠕变模型的建立

2.1 基于分数阶导数的流变元件

分数阶微积分最常用的定义为Riemann-Liouville(后面简称为R-L)分数阶微积分的定义方法[31]，其定义为:设f在(0，+∞)上逐段连续，且在(0，+∞)的任何子区间上可积，对t>0，Re(γ)>0，则函数f(t)的γ阶R-L分数阶积分为

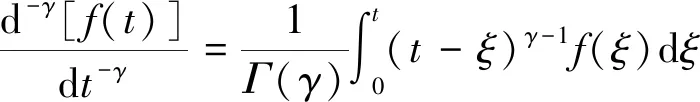
(1)

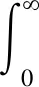
R-L分数阶导数为其积分的逆运算，定义为:设f∈C，ν>0，m为大于γ的最小整数，记ν=m-γ>0，则函数f(t)的γ阶R-L分数阶导数为

(2)

Abel黏壶元件是一种可用于描述介于理想弹性体和牛顿流体之间的物体力学性质的黏性元件，Abel黏壶的本构方程为

σ=ηdβε(t)/dtβ(0≤β≤1)

(3)

式中，β为求导阶数;η为黏滞系数。

由以上R-L型分数阶微积分理论，可反算得到

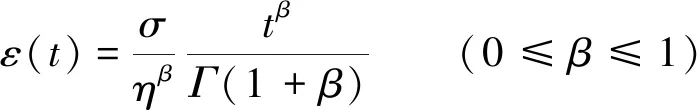
(4)

2.2 加速蠕变启动元件

软弱岩体的现场流变试验结果表明，岩石是否发生加速蠕变与加载的应力水平有关。存在某一加速蠕变应力阈值，当应力水平小于该阈值时，岩石的蠕变只有衰减蠕变阶段和稳定蠕变阶段;而当应力水平大于该阈值后，岩石的蠕变在经历衰减蠕变阶段和稳定蠕变阶段后会进入加速蠕变阶段。徐卫亚等提出的NVPB元件即考虑了当应力水平高于加速蠕变应力阈值σs时岩石的加速蠕变规律。各种岩石蠕变试验结果也表明，不同岩石进入加速蠕变的时间各不相同，而加速蠕变启动时间的选择会影响到各流变力学参数的计算结果。因而，张治亮等[39]认为在NVPB元件上还应存在加速蠕变启动时间点，即由稳定蠕变阶段向加速蠕变阶段过渡的时间点，进而提出了一种新的非线性黏塑性蠕变元件，即为NAVPB体。元件示意如图5所示。

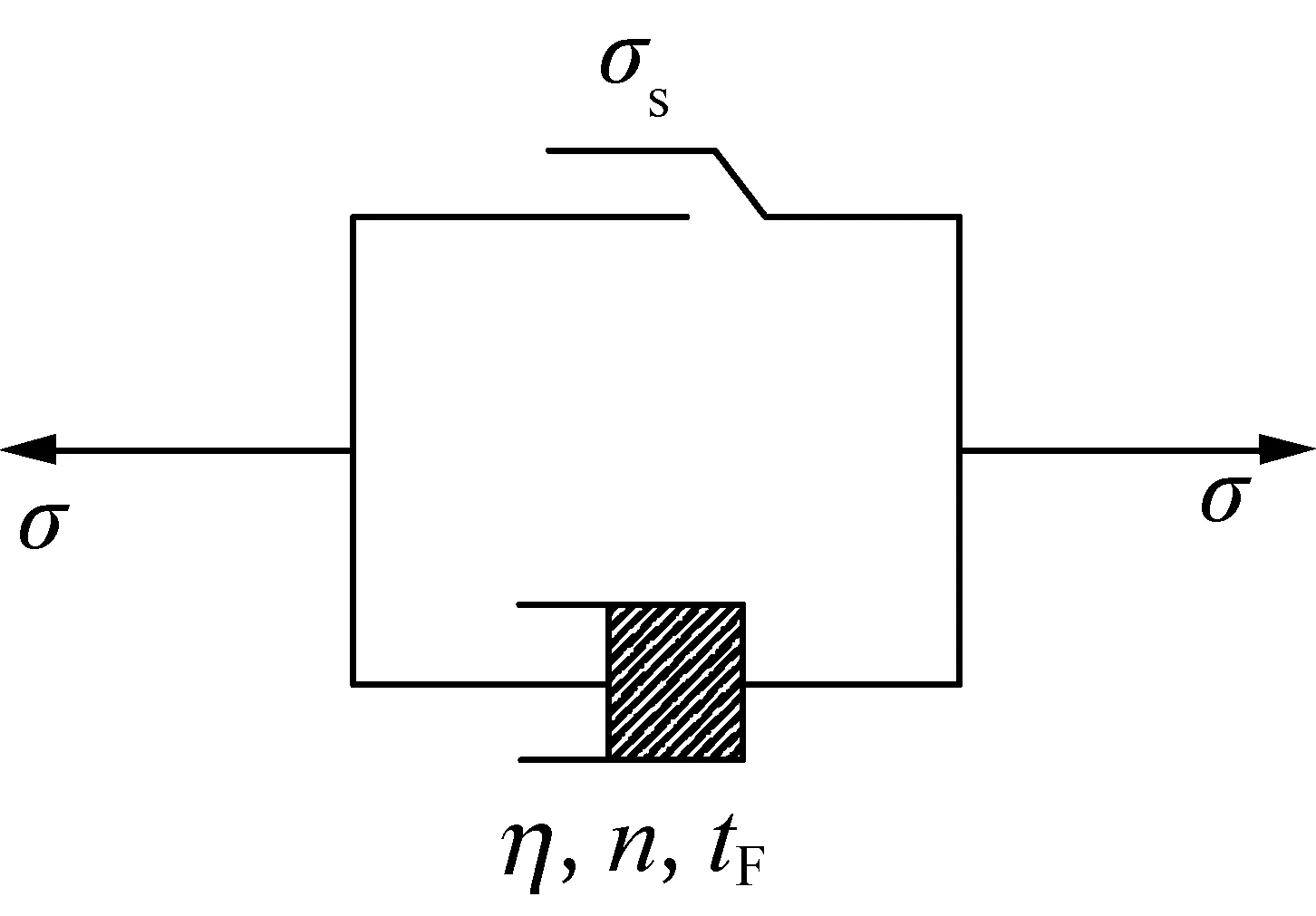
图5 非线性蠕变元件示意Fig.5 Sketch of nonlinear creep component

NAVPB体满足如下关系式

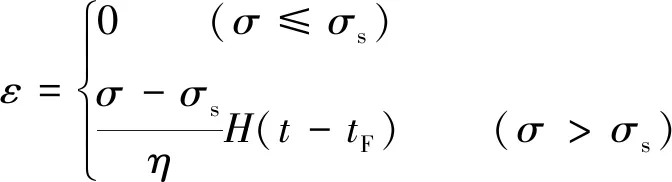
(5)

其中，σ为应力值;σs为加速蠕变应力阈值;η为塑性参数;tF为加速蠕变启动时间点。其中算子H(t)满足以下关系式

(6)

式中，n为流变指数，为大于0的整数。

2.3 非线性分数阶蠕变模型的建立

由1.4节的试验结果可知，当应力小于加速蠕变应力阈值时，岩石有瞬时弹性应变，并先后经历衰减蠕变阶段和稳定蠕变阶段，稳定蠕变阶段的蠕变速率趋于非零常数，基本符合传统的Burgers模型描述的岩石蠕变特征。前文讲到，当0≤β≤1时，Abel黏壶可用于描述介于理想弹性体和牛顿流体之间的物体力学性质，因此可以认为是一个包含弹性元件和黏性元件的综合元件[30]，而Burgers模型中的Kelvin体正是描述岩石的粘弹性应变特征，因此推测Abel黏壶元件也能较好地表征岩体的粘弹性变形特征，且相对Burgers模型中的Kelvin体而言为单个元件，结构更加简单，据此对Burgers模型进行第1步改进，即采用Abel黏壶元件替代Burgers模型中的Kelvin体。当应力大于加速蠕变应力阈值后，岩石在经历前两阶段的蠕变变形后，最终会在某一时间点进入非线性的加速蠕变阶段，而传统Burgers模型中的元件均为线性元件，无法描述非线性加速蠕变特征，为解决改进后的模型仍无法描述岩体加速蠕变阶段的变形特性这一问题，采用了在模型上串联NAVPB(非线性粘塑性蠕变元件)的方法继续对传统Burgers模型进行了第2次改进。

综上，为了能全面描述岩石各阶段蠕变特征，且使流变本构模型结构相对简单，采用Abel黏壶替代Burgers模型中Kelvin体，并串联上NAVPB元件，从而形成了现场软弱岩体的非线性分数阶蠕变模型。模型示意如图6所示。

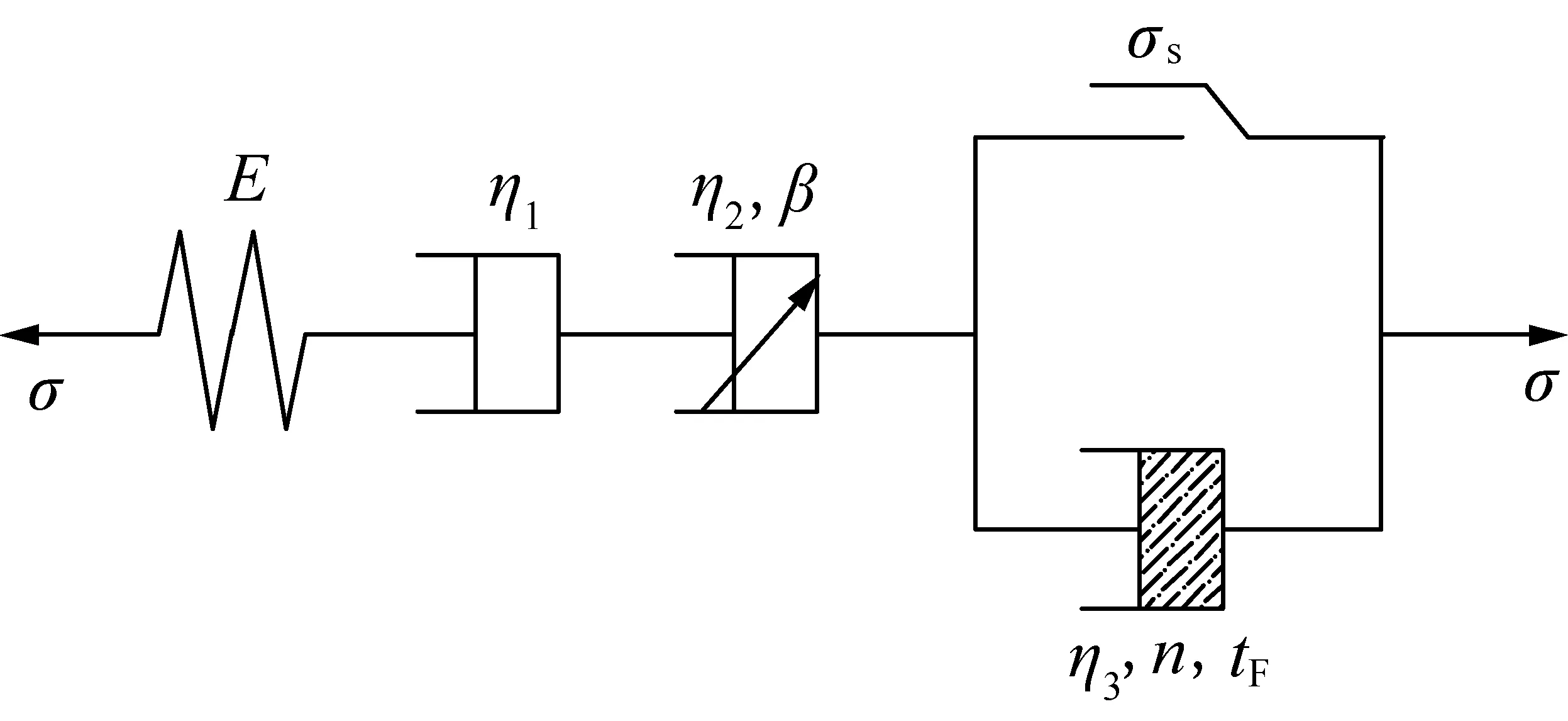
图6 非线性分数阶蠕变模型示意Fig.6 Sketch of nonlinear fractional derivative creep model

图6所示的蠕变模型有如下所示的本构关系:

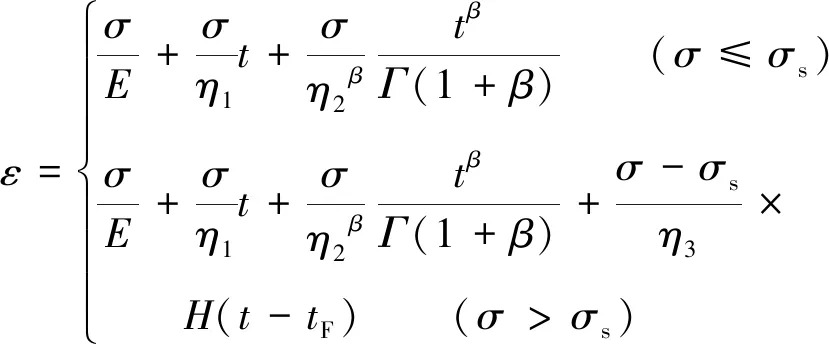
(7)

构建的非线性分数阶蠕变模型有如图7所示的蠕变特征曲线。

3 流变模型参数的确定及其验证

现场软弱岩体试样的各级应力蠕变曲线如图4(a)所示，现对各应力水平的蠕变试验数据进行Burgers模型和非线性分数阶模型参数的拟合与对比分析。在3.75～7.50 MPa应力作用下，由于应力水平不大于加速蠕变应力阈值,岩石蠕变经历了衰减、稳态蠕变阶段，采用式(7)进行蠕变参数的拟合分析;在8.75 MPa应力作用下，由于应力水平大于加速蠕变应力阈值,岩石蠕变经历了衰减蠕变阶段、稳态蠕变阶段和加速蠕变阶段，由蠕变速率的变化分析，在第15 h时，蠕变速率快速增大到1.68×10-3h-1，几乎达到这之前的3倍，之后更是迅速增大，因此取加速蠕变启动时间tF=15 h，采用式(8)进行蠕变参数的拟合分析。在Origin软件内分别编入Burgers模型和非线性分数阶模型的数学关系式，采用Levenberg-Marquardt方法，分别对各应力水平试验数据进行Burgers模型和非线性分数阶模型流变参数的拟合与对比分析。试验数据与拟合曲线如图8所示。拟合参数见表2。

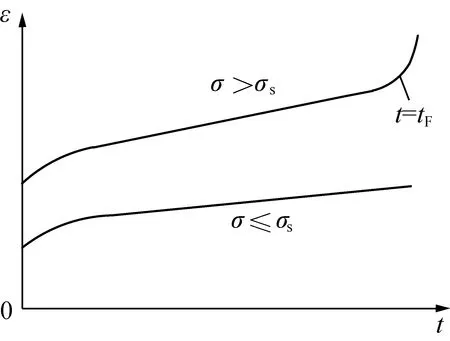
图7 蠕变特征全程曲线Fig.7 Complete curve of rock creep characteristic

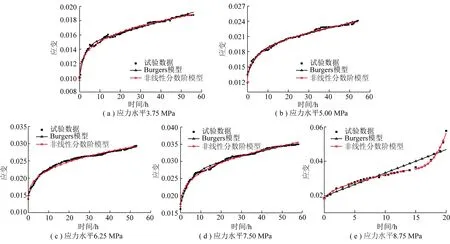
图8 试验数据与模型拟合曲线Fig.8 Experimental data and the fitting curves of the model

表2 不同应力水平下2种模型参数拟合结果
Table 2 Parameters fitting results of two creep models under different stress level

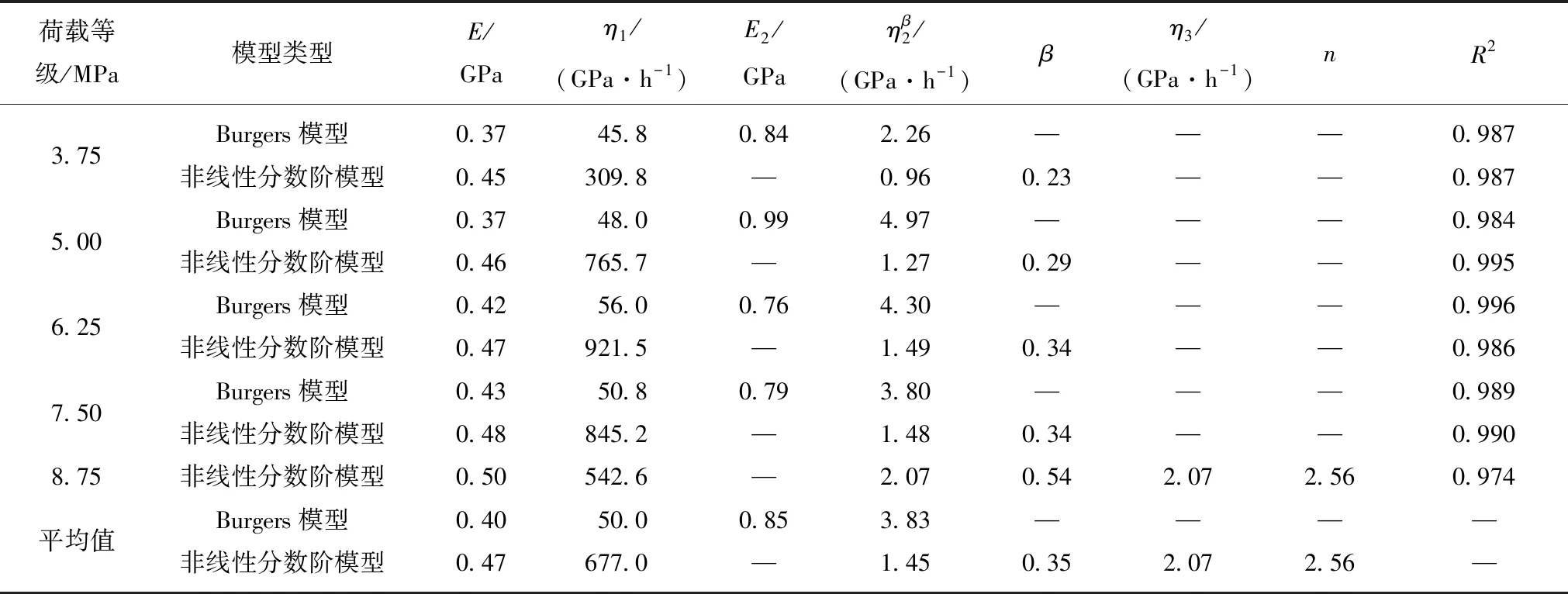
荷载等级/MPa模型类型E/GPaη1/(GPa·h-1)E2/GPaηβ2/(GPa·h-1)βη3/(GPa·h-1)nR23.75 Burgers模型0.3745.80.842.26———0.987非线性分数阶模型0.45309.8—0.960.23——0.9875.00Burgers模型0.3748.00.994.97———0.984非线性分数阶模型0.46765.7—1.270.29——0.9956.25Burgers模型0.4256.00.764.30———0.996非线性分数阶模型0.47921.5—1.490.34——0.9867.50Burgers模型0.4350.80.793.80———0.989非线性分数阶模型0.48845.2—1.480.34——0.9908.75非线性分数阶模型0.50542.6—2.070.542.072.560.974平均值Burgers模型0.4050.00.853.83————非线性分数阶模型0.47677.0—1.450.352.072.56—

由流变参数拟合结果可知:当应力水平不大于加速蠕变应力阈值7.50 MPa时，非线性分数阶蠕变模型和传统Burgers模型对试验数据都具有很好的拟合效果，且综合对比各拟合优度值发现，非线性分数阶蠕变模型拟合效果更佳。当应力水平大于加速蠕变应力阈值7.50 MPa时，传统Burgers模型并不能描述岩体 时间点之后的变形趋势，而非线性分数阶蠕变模型则能很好地拟合该应力水平下的全阶段变形数据。

综上，本文提出的非线性分数阶蠕变模型可以较好地描述现场软弱岩体包括加速蠕变阶段在内的全阶段蠕变特征，研究结果对相关工程具有一定的应用价值。

4 结 论

(1)软弱岩体试样的现场蠕变试验结果表明:应力水平不高于加速蠕变应力阈值时，岩体试样有瞬时弹性应变，随后经历衰变蠕变阶段和稳定蠕变阶段，且稳定蠕变速率不为零;应力水平超过加速蠕变应力阈值时，岩体试样经历完整的3阶段蠕变并最终发生破坏，且存在加速蠕变启动点。

(2)采用Abel黏壶替代Burgers模型中的Kelvin体，并串联上NAVPB元件，形成新的岩石流变本构模型-非线性分数阶蠕变本构模型，模型结构较为简单，且理论上能描述岩石的各应力水平各蠕变阶段变形规律。

(3)对试验数据的拟合结果表明:提出的非线性分数阶蠕变模型能更好地描述现场软弱岩体包括加速蠕变阶段的全阶段蠕变变形特征。研究结果对相关工程具有一定的应用价值。