解构与重构数学问题的五分法

姬梁飞

(华中科技大学，湖北 武汉 430074)

一般地，数学问题是数学学习的重心，也是推动数学发展与应用的重要推力。数学的发展是一个发现问题和解决问题的长期渐进过程，期间涌现了许多像四色猜想、哥尼斯堡土桥问题等。科学的解题活动不仅能够促进学生形成技能、培养能力，而且有助于形成良好的个性和思维品质。著名数学教育家波利亚曾强调：在解题过程中，需要善于分离问题的主要部分[1]。开展问题解决活动，如何调动学生广阔的思维和鲜活的经验，这需要掌握处理数学问题的基本方法。反思人们种种解决数学问题的过程和经验，会发现：能够用快速而简明的手法剖析、分解、重构错综复杂的问题，然后集中精力解决问题的核心部分和关键环节，这是多么的重要！然而，这个问题在现实教学中似乎并没有引起重视。在数学学习过程中，应培养学生具备对问题进行简捷而有序地转化和分解的本领。加强数学问题和思维活动之间的紧密联系，掌握处理数学问题的基本方法，具备对问题进行转化和推理能力，这也是数学教育应着重培养学生的一种数学素养。

1 分类讨论：聚焦问题的关键特征

面临错综复杂的问题，若去顾及问题的方方面面，一般很难直接处理。但有一点，一切事物均具有其共性和个性。共性是某类事物具备的普遍性质，决定事物的基本性质；个性是某一事物具有的特殊性质，揭示事物间的差异。抽离出数学问题所研究的数学对象，然后依据其本质属性(共性和个性)进行分类，这样就可以快速聚焦问题的关键特征。依据数学对象的共性与个性，可以将某些数学概念、数学定理、运算法则等进行分类。比如复数可以分成实数与虚数，抛物线按照其开口方向可以分成四类，讨论函数单调性可按自变量取值范围分成几种情况等。此外，参变量的不同取值范围导致的不同结果、数学问题的结论存在多种可能性等，这些都会导致分类讨论。分类的原则要求标准统一、互斥完备、多层分类、逐级递次等[2]。

例1 一只小蚂蚁E沿着某个矩形边框ABCD爬行，它从顶点A出发，依次经过其它三个顶点，再回到起点A。其中AB=2，BC=1。若m表示小蚂蚁E爬行的路程，n表示AE的长度，求m、n之间的关系。

解析 通过数学抽象，易知，研究问题是关于变量m、n的函数关系，依据研究对象的个性特征，可将研究对象m进行分类，即点E所处的位置或取值范围，宜分成四类。①若点E在线段AB上，此时n=m，m∈[0,2]；②若点E在线段BC上，此时n= 4+(m-2)2，m∈(2,3]；③若点E在线段CD上，此时n= 1+(5-m)2，m∈(3,5]；④若点E在线段DA上，此时n=6-m，m∈(5,6]。

数学问题的解决一般经历了低级到高级、静态到动态的过程。随着学生知识经验的不断丰富，学生观察与处理问题的主动性及其能力也在不断地提升。曹才翰认为数学教育归根结底是一种文化素质教育，而动态性是数学素质的精髓[3]。培养学生洞察事物的动态性、内外部联系、关键特征以及物化结构，有利于发展学生的数学素质。分类讨论方法是研究数学对象的共性与差异，通过去粗取精，由表及里，聚焦其关键特征，抓住事物的本质及其主要关系，是推动数学问题得到有效解决的利器。

2 分离提取：转换问题的表征视角

人类在实践活动中，为了研究事物间的数量关系或事物变化规律，往往需要从量的方面刻画事物运动规律。当事物关系中涉及多种数量关系时，有必要对事物的量进行分离、转化及提取。在数学中，常量和变量是表征事物量的一对范畴。从辩证法上看，静止与运动是对立统一的，常量与变量的界定在一定条件或视角下是可以相互转换的。通过对事物量的分离和提取，能够明晰事物关系，转换解决问题的视角，从混沌走向简明。

分离提取法，能够转换问题的表征视角，常用手法有二种。第一种是分离常量法。将某一整体的量或算式进行适当分离，从多重变量中抽离出单一变量，化繁为简。

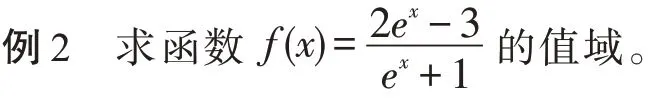
第二种是分离变量法。函数是刻画变量运动规律的一种工具，可以解决许多关于变量运动的问题。但对于游离函数本身之外的变量，若采用传统方法未必奏效。分离变量是对函数思想的深化认识。通过分离自变量与参变量，使得参变量游离函数自变量之外，若mf(x)对x∈R恒成立等价于m>f(x)max。

例4 若x>0,不等式mx2+(2m-4)x+m0恒成立，求m的取值范围。

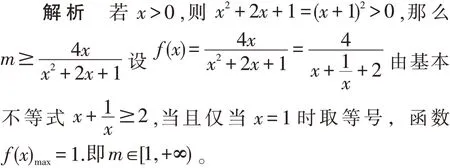
3 分解重组：解构问题的变式形式

从哲学上看，分解与重组既是对原问题的一种批判和否定，又是对原问题的一种改进和优化。通过打破现有结构形式，应用创新手法，从原问题中剥离出部分结构或元素，并将其打碎、分解、放缩、重构、模型化等方式处理，使之形成新问题或新形态。在数学中，分解与重组是一种分合法，即问题要素的分开与合并，是解决数学问题的一种常用方法。这种方法主要围绕数学问题的内涵特征、结构形式等进行解构重组、变式求解。它是明晰、转化问题形式的一种多元化手段，是对原问题和现有设计理念的深度思考。

此外，诸如an=Sn-Sn-1(n2),n·n!=(n+1)!-n!，等。可谓是执手分道去，各自还家门。分解重构是一种化解数学问题的方法，结合不同问题特点，重构手段、变式方法及设计方式也是多种多样，在形式上也是高度自由，不一而足。教师应引导学生了解多元化重构问题的方式方法，针对不同的主题设计出多样化重构方法或变式方法。在这个过程中，学生也能够迸发更多的变式创意，体验学习的快乐，从而形成自身独特的设计风格和数学素养。

4 分割入微：建构问题的境脉情景

整体与部分是一对哲学范畴，整体是部分的有机统一，部分则是整体的构成要素，二者相互依存、相互影响及相互转化。这就意味着一切客观事物都具有统一性和可分性，一切事物的形成过程可分割为若干部分。它的认识论意义揭示了深刻理解事物构成要素以及通过各要素逐步认识整体的重要性。部分与整体的关系也会受到外部条件的影响，二者关系也是动态变化的，处于持续的运动变化过程中。在数学中，不仅要把握数学问题，还要把握数学问题的组成要素、要素间的结构特征与结合方式。

在科学的认识活动中，分割能够使问题情境得到入微细化，建构解决问题镜脉。人们早期计算圆的面积，就采用了分割法，将圆形分割为尽可能多的小扇形，然后拼接为矩形。矩形的宽为圆的半径长r,矩形的长b为圆周2πr的一半，那么圆形面积为S=ab=r·πr=πr2。再者，分割法也是不断逼近目标的方法，可以采用分分割法寻求复杂方程或超越方程的近似解。因此，在数学问题中，分割使得原来问题关系结构中并不明显的单个要素变得突出，从部分研究整体，再从整体洞察部分。

由此可见，一方面，部分的分割入微是深入把握整体的基础，整体的高度把握又能进一步深化对部分的认识。另一方面，分割法是建构问题镜脉的一种工具，理解数学问题的语境文脉，探索数学知识的意蕴与背景。在教育环境下，搜索数学知识的意义，真正破解知识的“冰冷的美丽”，才能发挥学生主体“火热的思考”[4]，才能将知识转化与生成数学能力及素养。

5 分化超越：化解问题的核心方法

在解决问题时，一方面可将统一的事物分化为若干个相互独立的事物，以此对原问题进行瓦解与分裂，强调分而治之，各个击破；另一方面，又可将性质不同的事物升华为性质相同的新事物，新事物的结构、性质、功能等层面超越原事物，发挥其作为整体的性能，强调不破不立，革故鼎新。在认识世界时，分化与超越相互影响、相互渗透，不能只见分化不见超越，或只谈超越，忽略分化，而是把两者有机地结合起来。

解析 不妨设x10。这个函数就具备了新的功能，它在(0,+∞)上是单调递增的。同时把待解决问题转换为xg(x)>15，即f(x)>15，其中3f(3)=15。故原不等式的解集为(3,+∞)。通过对问题每个局部条件的深刻把握，将问题进行升华与超越，利用新事物的功能结构解决原有问题。

可见，分化与超越法是应用恰当的数学原理或准则对原问题的内部结构所进行的调整、分化、重构、超越等系列手法。通过这些可行性的操作，实现对问题的解析和化解，或设计问题重构的方案与原则。

综上所述，数学问题是引导学生学习数学的重要动力。著名数学家克莱因认为数学主要地是一种方法[5]。通过对数学问题的解构与重构，掌握基本数学方法，培养学生自主学习的兴趣，解决问题的数学能力。矛盾分析是解决事物矛盾问题的关键方法，应用矛盾分析和数学方法相结合的办法，创设数学问题的镜脉背景，提炼解决问题的思想方法。通过观察、猜想、推理、操作等思维活动，掌握分类讨论、分离提取、分解重组、分割入微、分化超越等基本技能方法，从而引导学生深层次地思考问题，多角度地分析和解决问题。