循环加卸载条件下脆性岩体裂纹演化规律

周详，李江腾

(中南大学资源与安全工程学院，湖南长沙，410083)

岩体是一种复杂介质，其中，层理[1]、节理[2]、裂隙等结构面非常复杂，岩体力学特性关系到工程的施工和运营安全，人们对其进行了大量研究，如CAO等[3-10]采用室内试验与数值模拟的方法，研究了预制单裂隙、断续双裂隙及多裂隙的岩石在单轴压缩下的裂纹扩展及破坏规律。而在实际工程应用中，岩石受三向应力作用，所以，研究在围压作用下裂隙岩石的裂纹扩展就更加具有实用性。肖桃李等[11-16]采用岩石及类岩石模型材料，研究了预制单裂隙和断续裂隙的岩石在三轴压缩试验下的破坏特征。然而，自然界中的岩体不仅承受着静态载荷作用，而且不同程度地承受着循环荷载的作用，所以，研究裂隙岩石在循环荷载作用下的力学特性对岩土工程具有重要意义。徐建光等[17]采用预制断续裂隙类砂岩模型对岩石在单轴循环荷载下的疲劳变化规律进行了探讨，并对影响裂隙试样疲劳变形的加载频率等因素进行了分析；LIU等[18]对不同应力幅值和不同节理倾角的节理岩样在三轴循环荷载下的力学行为进行了分析；LI等[19]采用断续预制裂隙模型研究了节理岩体在不同频率的动力循环荷载作用下的动态疲劳损伤特性，并建立了这类节理岩体的疲劳损伤模型。肖建清等[20]对十字交叉裂隙的类岩石进行了循环加卸载试验，对含不同几何特征的裂隙试样在静载和循环荷载下的强度、变形及破坏形态进行了试验研究，对试样的损伤累积演化规律进行了分析，并建立了相应的损伤演化方程。从以往研究可以发现，人们对含预制裂隙脆性岩石在循环荷载下的细观破裂演化研究很少，为此，本文作者首先对完整的大理岩的三轴压缩的试验结果进行对比，通过调整模型参数进行大量的模拟计算，直至获得一组能够较好反映大理岩力学行为的细观参数为止。在此基础上，对含有不同倾角的预制断续不平行双裂隙的大理岩进行三轴循环加卸载模拟，分析裂隙倾角和围压对大理岩的强度、裂纹扩展以及破坏特征的影响，以期为含节理裂隙的地下工程的稳定性研究提供参考。

1 试样的构建及细观参数验证

1.1 离散元模拟试样的构建

采用PFC3D软件建立的数值岩体模型的力学行为受到颗粒和接触模型细观参数的约束，通常采用平行黏结模型(BPM)[21]进行研究。在平行黏结模型中，平行键使颗粒相互黏结，在颗粒的接触处分别提供法向刚度和剪切刚度。图1 所示为BPM 的微观示意图及法向、剪切载荷下的平行键机理。当法向应力或剪切应力大于平行键强度时，平行键会断裂，使得颗粒间力的传递和微裂纹的扩展更加合理，因此，平行黏结模型更加适用于岩石脆性材料的研究。由PFC 软件生成的岩石模拟试样由粒径为1.20～1.992 mm 的23 186 个颗粒组成，岩石密度为2 670 kg/m3。模拟试验采用位移加载的方法进行峰前逐级加卸载，首先施加围压到预定值，并通过伺服控制，保持围压恒定，然后给上下“墙”以0.01 m/s 的速率进行轴向加载，加载到预定荷载30 MPa之后开始卸载，卸载至20 MPa 后再进行下一次加载。每次循环时，最大荷载增加10 MPa，直至达到峰值荷载为止，然后加载至轴应力为试样峰值强度70%时试验停止。在试验过程中，所加的预制裂隙长2a=20 mm，宽为1 mm，岩桥长2b=10 mm，倾角α分别为30°，45°，60°，75°和90°，见图2。

图1 BPM的微观示意图及平行键机理Fig.1 Schematic representation of BPM and mechanism of parallel bond bonds

1.2 细观参数验证

为了得到合理的试样模型，通过“试错法”对模型的颗粒流模型细观参数(表1)进行验证。图3所示为采用以上细观参数模拟的完整大理岩在不同围压(10，20 和30 MPa)作用下的应力-应变曲线，与相应的室内试验进行对比分析。由图3 可知：通过数值模拟获得的应力-应变曲线与室内试验所获得的应力-应变曲线变化趋势大致吻合，验证了模拟所使用的细观参数的合理性。

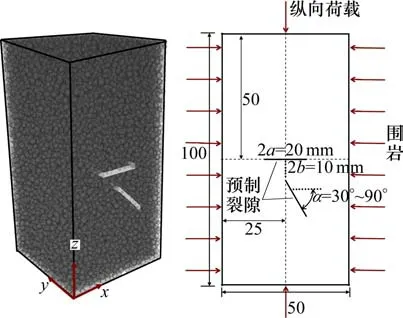
图2 预制裂隙试样模型Fig.2 Specimen model containing pre-existing crack

表1 PFC颗粒模型细观参数Table 1 Microscopic parameters of PFC model

图3 常规室内试验与PFC模拟应力-应变曲线对比Fig.3 Comparison of stress-strain curves between laboratory tests and PFC simulations

2 双裂隙大理岩宏观力学行为及细观力学响应

PFC颗粒模型细观参数见表1。采用颗粒流模拟双裂隙大理岩循环加卸载过程，对岩石的裂纹扩展及破坏模式进行分析，并对模拟过程中的轴向应力及微裂纹数量进行监测，同时可得到岩石的力链图，以便从细观角度对岩石的断裂损伤进行研究。

2.1 裂纹扩展结果分析

图4 所示为不同倾角预制裂隙及不同围压(0，5和20 MPa)循环加卸载下大理岩的裂纹扩展图。

从图4 可知：裂纹主要从预制裂隙的尖端萌生，沿最大主应力方向扩展；试样的最终裂纹扩展情况不仅受预制裂隙倾角的影响，同时，随着围压改变也会发生变化；当下部预制裂隙倾角α较小时，裂隙由水平裂隙的左端和倾斜裂隙的下尖端开始萌生；当下部预制裂隙倾角为75°和90°时，试样的裂纹扩展发生明显变化，裂纹主要沿水平裂隙左尖端和右尖端发生扩展。这种现象的产生可以通过图5所示的位移矢量图进行解释：当下部预制裂隙倾角为30°时，位移较大区域主要集中在水平预制裂隙左端及倾斜预制裂隙的下端；随着倾角增大为45°和60°，位移较大区域沿着下部预制裂隙向上移动，逐渐靠近上部预制裂隙；当倾角为75°和90°时，位移较大区域已经在水平预制裂隙的右尖端产生，由于位移错动而产生剪切作用，而下部预制裂隙处于位移相对均衡状态；随着倾角的变化，在水平预制裂隙的左尖端均会产生裂纹，这是由于预制裂隙布置方向及围压的共同作用，使水平预制裂隙左上方区域产生了位移错动带；倾斜预制裂纹右尖端的裂纹逐渐减少或者消失，可见水平预制裂隙对倾斜裂隙有一定的保护作用，且随着倾角增大，水平预制裂纹对倾斜预制裂纹的保护作用越明显；在相同倾角下，随着围压增加到20 MPa，试验的破裂模式没有发生较大变化；随着围压增大，裂纹的宽度小幅度变宽，岩石下部裂隙由沿着最大主应力方向变为向试件侧边扩展，这是因为围压增大使纵向拉裂纹的扩展受到限制，使得原来沿着最大主应力方向发展的裂纹发生偏斜。

图4 不同围压及倾角下的裂纹扩展结果Fig.4 Results of crack propagation under different confining pressures and fracture inclination α

图5 围压为10 MPa时的位移矢量图Fig.5 Displacement vector diagram under confining pressure of 10 MPa

2.2 应力应变及裂纹数量分析

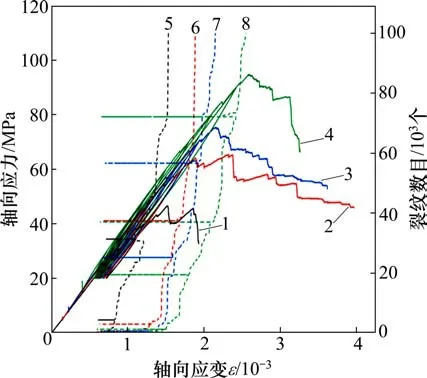
图6 轴向应力与微裂纹数量和轴向应变曲线(α=30°)Fig.6 Influence of axial strain on specimen's axial stress and crack number(α=30°)

当倾角α为30°时，预制裂隙在不同围压下循环加卸载大理岩的轴向应力应变及裂纹数量如图6所示。由图6可知：双裂隙大理岩在循环加卸载作用下，滞回环面积较小，形状也呈现出“尖叶状”；在加卸载应力突变时，滞回环出现尖点，反映了岩石的弹性变形响应迅速且占主导地位，而塑性变形不明显；卸载并重新加载至高一级别应力，且随循环次数或轴向应力不断增大，滞回环面积增大，能量耗散增加，累积不可逆变形增大；在加卸载过程中，微裂纹数量增大表现出明显的“记忆”行为；微裂纹数量基本保持不变；微裂纹数量在轴向应力达到峰值时急剧上升，这说明大量微裂隙在此阶段萌生，最终形成宏观裂隙；当试验结束时，裂纹数量随围压增大而增大，且增大的趋势逐渐减小。这是由于围压对试样的侧向变形形成了限制，导致其破坏难度增加，故试样内部产生的微裂纹大量增加；当倾斜裂隙倾角不变时，随着围压增大，试样的峰值强度也增大。

在不同围压下，裂隙倾角α对峰值强度的影响见图7(其中，Δ1，Δ2和Δ3为裂隙倾角改变所产生的峰值强度增大幅度)。从图7 可见：围压对峰值强度产生显著影响，且倾斜裂隙的角度对试件的峰值强度也有一定影响；当α从30°变为45°时，峰值强度小幅度增加；但当α增大为60°时，在不同围压下，峰值强度均显著提升，而当α＞60°时，峰值强度增加幅度又变小。这是由于随着倾斜裂隙倾角增大，当α≥60°时，2 条预制裂隙在最大主应力方向的投影长度变为水平预制裂隙长度，此时，倾斜裂隙对于试样受力的影响越来越小，试样的受拉区域越来越小，使得峰值强度的增长幅度在预制倾斜裂隙的倾角α＞60°时变小，而围压会抑制这种峰值强度增长幅度的变化趋势；当围压增加至20 MPa 时，α从45°变为60°，峰值强度的增长幅度并没有显著增大。

图7 不同围压下裂隙倾角α对峰值强度的影响Fig.7 Effect of fracture inclination α on peak strength under different confining pressures

当α=30°以及围压为20 MPa 时，微裂纹数量随循环次数的变化如图8所示。从图8可见在整个循环加卸载过程中，所有试样的微裂纹数量增长曲线都呈现出相同的变化规律：在循环加载初期，微裂纹的数量几乎为0；随着循环次数增加，微裂纹数量开始缓慢增大；当循环的上线应力接近峰值时，微裂纹数量开始急剧增大；围压及倾斜裂隙角度α不同，微裂纹数量在这个循环加载过程中也会表现出差异，围压越大，微裂纹数量急剧增长阶段向后推移；在相同的循环次数(循环加载上限应力相同)下，随围压增大，微裂纹数量越少；而在相同围压(20 MPa)下，倾角α越大，微裂纹数量曲线的缓慢增大阶段越长，如在第5 个循环时，α为30°和45°的试样的微裂纹数量已大幅度增多，而当α为60°，75°和90°时，试样微裂纹数量还在缓慢增大阶段，说明α为30°和45°的试样局部破坏开始发生，裂缝数量也急剧增加，岩石试样即将失稳破坏。

2.3 细观力场分析

图8 微裂纹数量与循环次数的关系Fig.8 Relationship between number of microcracks and cycle times

图9 不同围压及倾角α下的力链分布结果Fig.9 Results of force chain distribution under different confining pressures and fracture inclination α

图9所示为不同倾角预制裂隙及不同围压循环加卸载下大理岩的力链分布图，可用于对试验循环加卸载后试样内部损伤的细观力学机制进行分析。图9中，力链的粗细程度代表力的大小，力链越粗，表示力越大。从图9可明显地看出裂隙周围的应力集中，但当倾斜裂隙角度较小时，压应力主要集中于水平裂隙的左端和倾斜裂隙的下端；当倾斜裂隙角度为75°和90°时，压应力主要集中于水平裂隙的两端。这就从微观受力为出发点解释了下部预制裂隙倾角为75°和90°时试样的裂纹分布发生较大变化规律的原因。而造成应力集中区域发生变化的原因是预制裂隙在最大主应力方向的投影长度不同。倾角越大，力链密集越分布在水平预制裂纹两端，且倾斜预制裂纹下方力链越密，这更加表明随着倾角增大，水平预制裂纹对倾斜预制裂纹的保护作用增强。

3 结论

1)当预制裂隙倾角α为30°，45°和60°时，试样的裂纹扩展模式相近，裂隙主要由水平裂隙的左端和倾斜裂隙的下尖端开始萌生；当倾角α为75°和90°时，试样的裂纹扩展发生明显变化，裂纹主要沿水平裂隙左尖端和右尖端发生扩展。

2)预制双裂隙大理岩在循环加卸载作用下，裂纹数量随围压的增大而增大，且在整个循环加卸载过程中，微裂纹数量呈现出相同的增大规律；倾斜裂隙的角度α对试件的峰值强度也有一定影响，当α增大为60°时，在不同围压下的峰值强度均显著提升，而α＞60°后峰值强度增加的幅度又变小，而围压会抑制这种峰值强度增大幅度的变化趋势。

3)裂纹扩展随着围压的改变也会随之变化，水平预制裂隙对倾斜预制裂隙有一定的保护作用。随着倾角增大，水平预制裂纹对倾斜预制裂纹的保护作用越明显。