交流电力测功机的支持向量机模糊PID控制策略

钟定清，王艾伦，何谦，魏克湘，唐勇

(1.中南大学机电工程学院，湖南长沙，410083；2.湖南工程学院机械工程学院，湖南湘潭，411104)

测功机主要包含水力测功机、电涡流测功机、电力测功机，用于测试动力传动系统的传递功率[1-2]。水力测功机的结构简单，但设备庞大，且效率低；电涡流测功机的结构复杂，控制难度大且控制精度低。与传统测功机相比，交流电力测功机具有结构简单、测试范围广、在实现动力传动系统测试的同时还可以实现能量回收等优点，因此，交流电力测功机得到普遍应用[3-5]。测功机的控制性能直接影响着动力传动系统测试技术的发展。测功机控制性能主要取决于控制精度、控制响应速度、控制可靠性等指标。国内针对测功机的研究起步较晚，直至20世纪60年代，国内各大科研院所开始测功机的研究，且主要集中在测试测功机的性能上。国外针对测功机的研究起步较早，主要集中在测功机的控制性能上。目前，随着计算机技术、控制理论、电子技术的研究不断成熟，电力测功机测试系统正在朝着集成化、智能化、网络化方向发展[6]。CHAVHAN 等[7]利用LabView软件设计了一种测功机测试台架的人际交互监控系统，该系统可完成测功机测试台架的系统控制以及数据采集。同时，研究人员将一些先进的控制策略逐渐应用于电力测功机上，包括自适应控制[8]、模糊控制[9]、神经网络控制[10]、PID控制[11]等。同时，一些新的控制策略包括变压变频控制[12]、矢量控制[13]、直接转矩控制[14]等被提出。由于交流电力测功机系统具有变负载的非线性时变特性，且传统控制策略自适应性与实时性较差，所以，传统控制策略对于交流电力测功机系统难以取得较好的控制效果。为了提高交流电力测功机运行的稳定性和控制精度，本文作者结合支持向量回归预测、模糊控制、PID 控制这3 种理论，提出一种支持向量机模糊PID控制策略。

1 SVR-Fuzzy-PID控制模型

1.1 PID控制

PID控制因结构简单、稳定性高、调整方便等优点已经成为目前应用较广泛的控制方法[15-16]。PID控制由比例(P)、微分(I)以及积分(D)单元构成，它的输入和输出关系为

式中：e(t)为被控制参数的实际值和设定值的偏差，是PID 控制器的输入量；u为控制信号，即PID 控制器的输出量；Ti为积分时间常数；Td为微分时间常数；Kp为比例增益。

对式(1)进行离散化，有

式中：u(k)为系统在k时刻的控制量；e(k)为误差；Δe(k)为误差变化率；Kp为比例系数；Ki为积分时间常数；Kd为微分时间常数。

在运行过程中，将偏差不断消除是PID控制器的功能，偏差e(t)反映实际输出值y(t)偏离参考值r(t)的程度。偏差e(t)经过PID控制的比例处理、积分处理和微分处理之后，利用加权之后的结果作为被控对象的输入，可以达到调整系统的响应和消除系统偏差的目的。PID 控制器原理如图1所示。

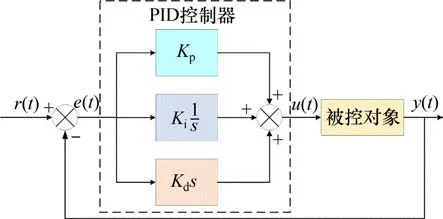
图1 PID控制器原理图Fig.1 Schematic diagram of PID controller

降低PID控制器的稳态误差和提高响应速度的方法之一是调整Kp，Ki和Kd这3个参数，本文利用模糊算法对这3个参数进行优化。

1.2 Fuzzy-PID控制

模糊(Fuzzy)控制是通过利用模糊逻辑语言及逻辑关系进行模糊推理，从而摆脱对精确数学模型的依赖，其具体的工作流程如图2 所示。从图2可看出模糊控制器主要由模糊规则库、模糊器、模糊推理机以及解模糊器组成[17-18]。

图2 模糊控制流程Fig.2 Schematic diagram of fuzzy controller

表1 Kp的模糊规则表Table 1 Fuzzy rule for Kp

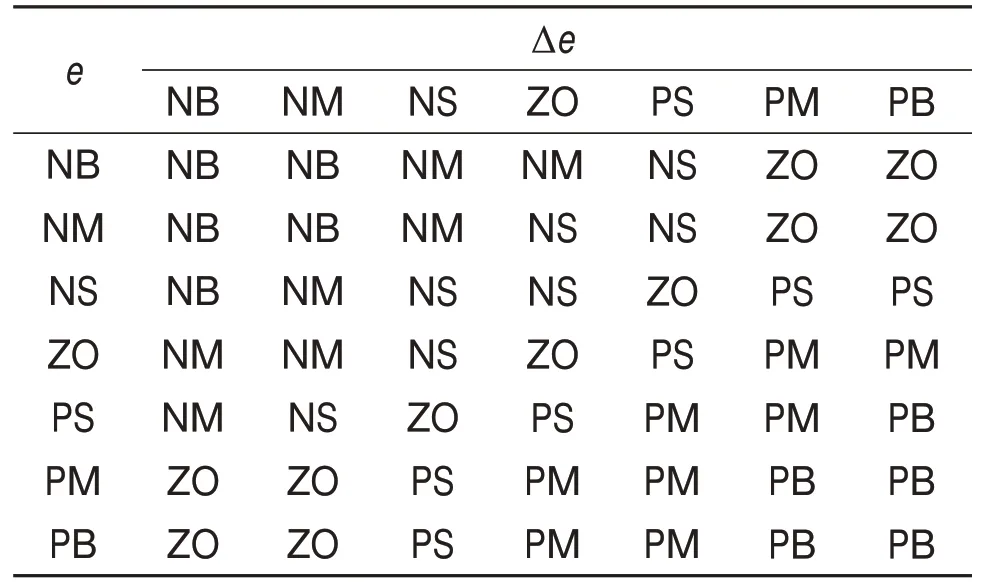
表2 Ki的模糊规则表Table 2 Fuzzy rule for Ki

表3 Kd的模糊规则表Table 3 Fuzzy rule for Kd

Kp，Ki和Kd的模糊规则分别如表1～3 所示，其中，NB，NM，NS，ZO，PS，PM 和PB 为e(k)和Δe(k)的模糊子集，分别表示负大、负中、负小、零、正小、正中、正大。传统的PID 控制器中Kp，Ki和Kd这3个参数往往是固定不变的，在实际工作过程中无法实时进行调整。模糊PID 控制器是以e(k)和Δe(k)为输入量，以Kp，Ki和Kd为输出量，通过表1～3中的模糊规则对Kp，Ki和Kd进行自整定，其主要工作原理如图3所示。

图3 Fuzzy-PID控制器原理图Fig.3 Schematic diagram of Fuzzy-PID controller

由于e(k)，Δe(k)，Kp，Ki和Kd均服从正态分布，可以得到相应的隶属度函数，利用模糊规则即可调整PID的Kp，Ki和Kd：

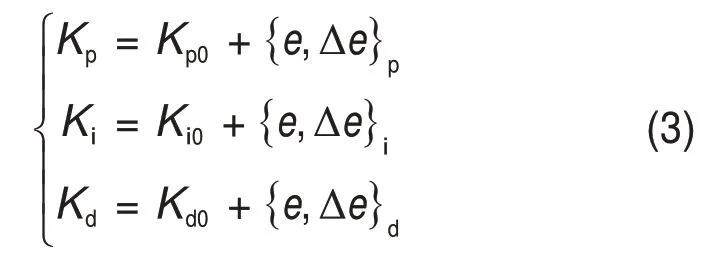
PID控制器的新控制参数为Kp，Ki和Kd，其计算规则如下：在模糊控制器中利用模糊规则以e(k)和Δe(k)为输入量，得到Kp，Ki和Kd的相应调整量{e,Δe}p，{e,Δe}i和{e,Δe}d，之后将计算得到的调整量与初始值Kp0，Ki0和Kd0叠加即可得到新控制参数。

1.3 SVR-Fuzzy-PID控制

将支持向量机(support vector machine，SVM)由分类问题推广至回归问题则可以得到支持向量回归方法(support vector regression，SVR)，此时，支持向量机的标准算法也被称为支持向量分类(support vector classification，SVC)[19-20]。SVC 中的超平面决策边界是SVR的回归模型：

式中：f(x)为观察值；X为输入向量；w为回归系数向量；b为常数。

SVR 具有稀疏性，若样本点足够接近回归模型的回归值，即落入回归模型的间隔边界内，则该样本不计算损失，对应的损失函数被称为ε-不敏感损失函数(ε-insensitive loss)：

式中：ε为决定间隔边界宽度的超参数。从式(5)可知不敏感损失函数与SVC 使用的铰链损失函数相似，在原点附近的部分取值被固定为0。类比软间隔SVM，SVR可表征为如下二次凸优化问题：

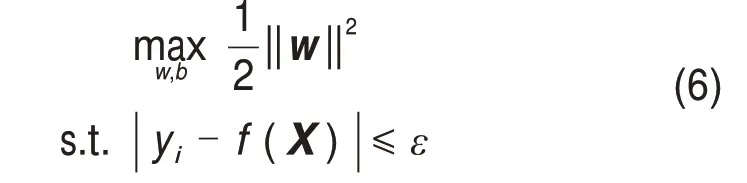
使用松弛变量ξ和ξ*表示样本偏离ε-不敏感损失函数程度后可得：

其中：C为惩罚因子。通过引入拉格朗日乘子α，α*，μ和μ*，可得到其拉格朗日函数和对偶问题：

其中，对偶问题有如下KKT条件：

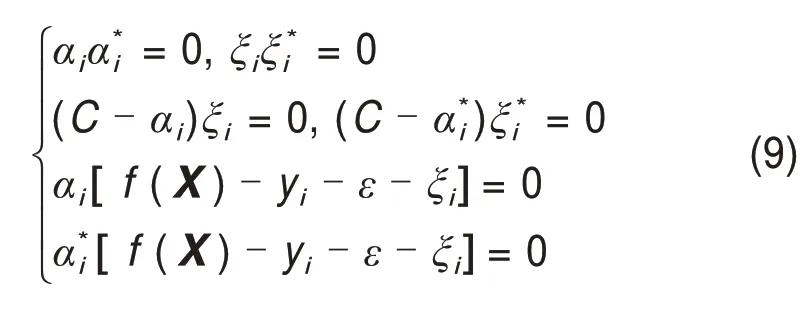
对该对偶问题进行求解，可以得到SVR 的形式：

SVR-Fuzzy-PID的控制原理如图4所示。SVRFuzzy-PID 控制器是在Fuzzy-PID 控制器的反馈回路中增加1 个SVR 预测器，该预测器的主要作用是采集输出y在时刻k之前的n+τ个连续采样数据作为预测器输入，输出的是该预测器预测PID控制器在k+m时刻的输出y(k+m)，并且以k+m时刻预测的输出y(k+m)替换PID控制器在k时刻的输出y(k)。同样地，在加入SVR预测器后，原来的Fuzzy-PID控制器输入偏差e(k)=r(k)-y(k)中的y(k)也被SVR预测期预测的y(k+m)所代替，新的计算预测误差e(k)=r(k)-y(k+m)。

图4 SVR-Fuzzy-PID控制器原理图Fig.4 Schematic diagram of SVR-Fuzzy-PID controller

2 仿真结果及分析

为了验证本文所提出的SVR-Fuzzy-PID控制器的效果，选择简单三阶系统将SVR-Fuzzy-PID控制器应用于稳定控制中，建立如图5所示模型，以此为基础进行仿真。假定描述该系统模型的传递函数为

图5 3阶控制模型Fig.5 Third-order control model

为了研究持续性干扰影响下的系统响应，当t=1 s时，在系统中加入强度为1的持续性干扰，系统的响应曲线如图6所示。为了研究暂时性干扰影响下的系统响应，当t=1 s 时，在系统中加入强度为1的干扰，并在t=1.2 s时将扰动撤去，系统的响应曲线如图7所示。

从图6 和图7 可以看到：SVR-Fuzzy-PID 控制器的控制性能比Fuzzy-PID 控制器和PID 控制器的控制性能好，主要表现在系统发生扰动时，SVRFuzzy-PID 控制器的响应更加迅速，因为控制器中加入了SVR 预测器，同时能够明显降低超调量以及缩短调整时间。在持续性扰动下，超调量大大降低，系统没有波动，且迅速恢复到平稳状态。在暂时性扰动下，加入了SVR预测器的Fuzzy-PID控制器的响应速度提高，同时，能够在扰动消失时迅速稳定系统。

图6 系统在持续性扰动下的响应曲线Fig.6 System response under continuous disturbance

图7 系统在暂时性扰动下的响应曲线Fig.7 System response under temporal disturbance

从图6 和图7 可以看出：PID 控制器、Fuzzy-PID 控制器、SVR-Fuzzy-PID 控制器的控制性能逐步提高。这主要是因为PID 控制器中加入了Fuzzy控制器，使得PID控制器中的Kp，Ki和Kd这3个参数可以根据系统的实际运行状况不断地得到调整，而引入了SVR控制器的Fuzzy-PID控制器具有前瞻性，使控制效果得到优化。

3 实验结果与分析

为了验证本文所建立的交流电力测功机的SVR-Fuzzy-PID控制器的控制性能，在实际系统的调试过程中进行具有代表性的转速动态响应试验以及稳定性试验。柴油机型号为AVL 5402，转速范围为800～2 000 r/min；测功机型号为FC 2012，额定转速为3 000 r/min，电压范围为0～500 V，电流范围为0～40 A，转子电阻为0.9 Ω，定子电阻为0.4 Ω。图8所示为实验原理图。

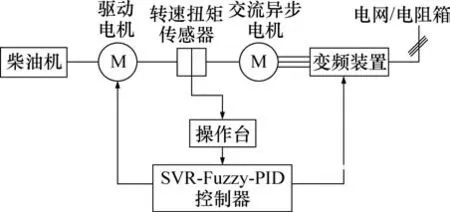
图8 实验原理图Fig.8 Schematic diagram of experiment

转速动态响应试验的主要实验由2 部分组成：1)初始状态下速度响应特性实验；2)在运行过程中，给定速度改变时系统的动态响应特性试验。在实验过程中，依次将被测发动机的油门调整到需要测验的位置，注意此时被测发动机要处于怠速状态，然后给系统的各个参数设置相应值。被测发动机此时的转速n为1 200 r/min，将初始测试点的转速设置为800 r/min。完成上述设置后，启动控制系统程序，此时，转速的动态响应如图9所示。为进一步探讨过渡过程中系统的动态调节品质，在速度突变的情况下进行系统的动态响应特性试验，发现当转速n=1 200 r/min 时，被测发动机的油门开度维持不变。将转速n=1 500 r/min 设为设定值，转速突变时转速动态响应如图10所示。

图9 系统初始运行转速动态响应Fig.9 Systm response of initial running speed

本文的稳定性试验还包含虑了超速试验，转速上限设定为1 900 r/min。随着试验的进行，被测发动机的转速达1 800 r/min；当转速接近或超过警戒值1 900 r/min时，SVR-Fuzzy-PID控制器开始工作(此时，油门开度维持恒定)；若继续增加转速并使之超过1 900 r/min，此时，油门开度维持恒定；当转速增加至2 100 r/min时，被测发动机测功系统的负载会自行增加，进而使得被测发动机回到转速1 900 r/min以下状态运行，系统趋于稳定，如图11所示。

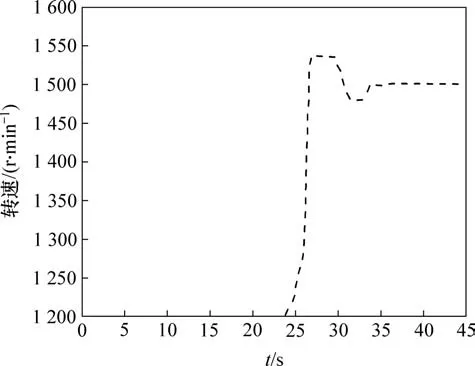
图10 转速突变时转速动态响应Fig.10 Speed response under speed mutation

图11 稳定性试验结果Fig.11 Results of stability test

从试验结果可以看出：SVR-Fuzzy-PID控制器的动态响应快速，超调量很小，稳态误差控制精度高，抗干扰能力强。总的来说，本文设计的SVR-Fuzzy-PID控制器可以较好地满足交流电力测功系统的控制需求。

4 结论

1)通过结合SVR预测、Fuzzy控制、PID控制设计了一种针对交流电力测功机的SVR-Fuzzy-PID控制器。

2)在SVR-Fuzzy-PID 控制器中，模糊规则可持续调节PID 的参数Kp，Ki和Kd。将SVR 放在反馈环节可实现“超前”控制，以解决传统控制系统的控制滞后问题。

3)与传统PID 控制器比，本文所设计的SVRFuzzy-PID 控制器可以使交流电力测功机的响应速度提高，同时，整个系统的稳定性也得到一定提升。