台风区钢管格构支架稳定性和优化设计分析
王保良
(中铁建大桥工程局集团第四工程有限公司 黑龙江哈尔滨 150000)
1 引言
钢管格构支架体系在大跨度桥梁施工中有着广泛的应用。然而,当支架结构达到一定高度时,结构体系变得柔性化,其力学性能也较为复杂。目前,在桥梁施工支架的施工工艺和技术、设计计算和工程应用方面已取得一些研究成果[1-4]。而在台风区,由于风荷载作用,柔性钢管格构支架的稳定性和安全性也变得非常重要[5]。平潭海峡大练岛特大桥新建工程中现浇公路桥梁的钢管格构支架系统,由于处于风速14 m/s台风地区,故主要分析风荷载对钢管格架支架体系的影响,对钢管格构支架的稳定性进行计算,最后建立有限元模型进行主要影响参数分析,对钢管格构支架结构进行优化设计分析,最后通过风洞试验进行验证。
2 工程背景
大练岛特大桥新建工程,位于平潭海峡中部,距大陆最近点7.85 km。全年风力较大、水道泛涌。大练岛特大桥公路部分共五联,每联布置形式为4×40 m+4×40 m+6×40 m+5×40 m+4×32 m的连续梁桥,共23跨,其中桥墩高度在13~50.5 m之间,主梁采用现浇支架施工。现浇支架采用“钢管格构支架+贝雷梁”结构体系,D0~D9号钢管格构支架立柱采用φ720×14 mm钢管,跨中钢管之间平联和斜撑采用φ400×8 mm钢管联结。D10~D19号钢管立柱采用φ1200×14 mm钢管,跨中平联采用φ720×14 mm钢管,斜撑采用φ400×8 mm钢管。选取最高钢管格构支架D10~D11号段(支架高度为61.702 m)为研究对象,钢管格构支架结构现场布置以及纵横桥向布置如图1~图2所示。

图1 钢管格构支架现场布置

图2 钢管格构支架纵横桥向布置(单位:mm)
3 有限元模型的建立
对整个支架体系进行结构离散化,桁架节点、格构柱节点处划分节点,结构计算分析特征位置处节点,与周围结构或地基连接处设置节点,按照实际钢结构划分相应的单元[6-7]。
采用Midas Civil软件建立支架整体模型,贝雷梁部分采用桁架单元,支架部分采用梁单元,整体模型划分为6 993个单元,3 688个节点,其中贝雷梁部分6 628个单元,横担梁104个单元,立柱108个单元,平联85个单元,斜撑68个单元。钢管格构支架整体有限元模型如图3所示。钢管格构支架工作状态最大风荷载按8级风考虑,风速为20.7 m/s;非工作状态风荷载按十年一遇台风考虑,风速为45.4 m/s。

图3 钢管格构支架整体有限元模型
4 钢管格构支架设计计算及稳定性分析
按照混凝土浇筑不同工况对支架强度、刚度和稳定性进行分析计算,每种工况对应的荷载组合见表1。

表1 各工况说明
对贝雷梁、横梁、立柱、支架联接系(平联与斜撑)进行验算,在各工况下,支架中贝雷梁的主弦杆最大轴力为-390.16 kN,竖杆最大轴力为-192.13 kN,斜杆最大轴力为139.15 kN,立柱的最大应力为-126.81 MPa,最大位移为21.46 mm。支架联结系剪力最大值为-150.41 kN,应力最大值为-84.14 MPa。贝雷梁上、下弦杆的设计值为510 kN,立柱设计值193 kN,斜撑设计值为156 kN,Q235钢材的抗压设计值195 MPa,故实际荷载均小于设计承载能力,支架的强度满足设计要求。
5 钢管格构支架结构优化设计
5.1 钢管直径的影响
假设支架立柱是等截面直杆,压力作用线与截面的形心纵轴线重合且材料是完全均匀、弹性的,由欧拉临界力公式可求得立柱的临界荷载[8-9]。将钢管的壁厚δ与直径d的比值作为控制参数,通过求解不同直径不同壁厚立柱的屈曲稳定系数,得出最合理的钢管直径以及壁厚,不同δ/d的钢管格构支架屈曲稳定系数对比如图4所示。

图4 不同δ/d的钢管格构支架屈曲稳定系数对比
由图4可以看出,当钢管结构的δ/d一定时,结构的临界屈曲荷载系数随着钢管直径的增大而增大,并且直径越大其增长越大,整体呈指数上升趋势;当钢管的直径为定值时,随着壁厚的增加,即参数δ/d变大,支架结构的临界荷载系数也相应增大,并且直径越大其变化值越大,说明结构的截面尺寸是影响其稳定性的主导因素。
5.2 肢数的影响
按照桥梁钢管格构支架施工设计图纸,采用φ1 200 mm钢管作为立柱,φ720 mm钢管作为平联、φ400 mm钢管作为斜撑,主要研究支架结构的肢数对稳定性的影响[10-11],通过建立单肢、双肢、四肢、六肢的有限元模型,得到每种结构的临界荷载系数,不同肢数支架结构临界荷载系数见表2,不同肢数支架模型屈曲如图5所示。
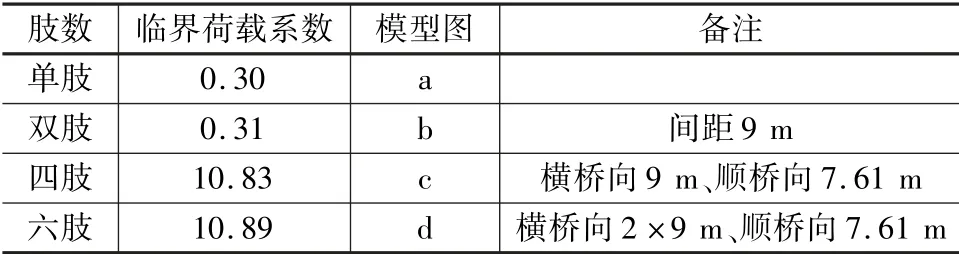
表2 不同肢数支架结构临界荷载系数

图5 不同肢数支架模型屈曲图
由表2和图5支架模型屈曲图可知,单肢和双肢钢管柱的临界荷载系数基本相同,说明双肢格构支架与单肢的相比,稳定性提高不大,但是当肢数增加到四肢时,其临界荷载系数提高相当大,此时的钢管格构支架稳定性较好,同时抵抗外荷载能力较高,当肢数增加到六肢时,支架临界荷载系数反而增加不大,表明四肢钢管格构支架是最经济的选择。
5.3 节段高度和总高度的影响
当支架的高度较高时,一般需要将支架进行分节[12-13],现对9 m、12 m、15 m、18 m不同的节段高度,支架总高度为30 m、40 m、50 m、60 m、70 m、80 m的临界荷载系数进行分析,得到支架结构前三阶屈曲状态下的临界荷载系数(见表3)。

表3 不同节段长度支架临界荷载系数
从表3中可以看出,无论结构的节段高度如何变化,其第三阶荷载临界系数均比前两阶大很多,说明该结构较难达到其三阶的失稳破坏,破坏形式主要发生在结构的前两阶。在同一节段高度下,结构的临界荷载系数随着总高度的增加呈现下降趋势,说明其稳定性越差,但当结构的节段长度不大于18 m时,结构的临界荷载系数能保证大于4.0,基本能满足结构的稳定性要求。当支架的总高度一定时,其节段长度越小,即结构的刚度会变大,整体稳定性也随之增大,故结构临界荷载系数越大。但是当支架总高度大于70 m时,结构的一阶临界系数下降幅度变快。在支架设计时,可以根据不同的临界系数的要求来选取合理的支架节段高度和支架总高度。
5.4 纵横向间距的影响
钢管格构支架纵横向间距是反映支架支撑面积的重要指标,为了研究纵横向间距对其稳定性的影响,采用节段高度为12 m,总高度为60 m的钢管格构支架,通过变化不同的纵横向间距(纵横向间距取相同值)求得支架的临界荷载系数(见表4)。
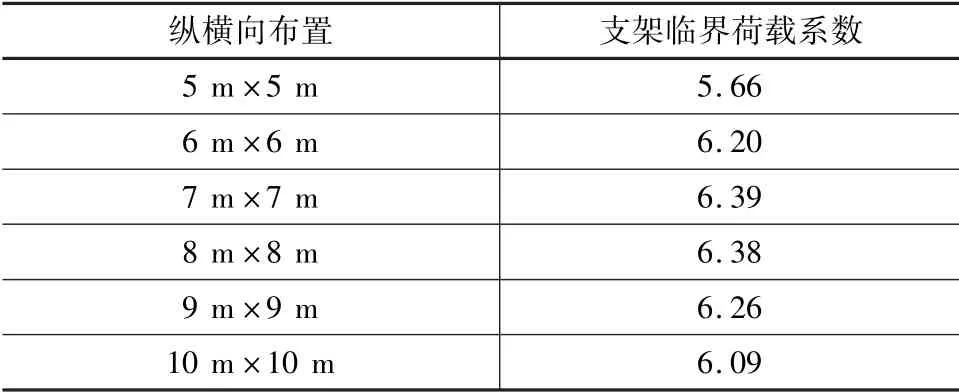
表4 不同间距荷载临界系数
由表4可知,格构柱支架的临界荷载系数随着纵横向间距的变化呈现抛物线变化趋势,当间距小于6 m时,其变化较快,接近直线递增;支架间距在6~7 m时其上升幅度较小;当格构支架间距达到7 m时,其临界荷载系数达到峰值;当间距大于7 m后其值开始平稳下降。说明支架纵横向间距在7 m左右时稳定性最好,有利于钢管格构支架的安全性。
6 钢管格构支架风洞试验
由于钢管格构支架尺寸较大,足尺模型风洞试验很难实现,故采用缩尺模型进行风洞试验。试验模型选取四肢格构支架为研究对象,模型缩尺比1∶150,材料选用丙烯腈-丁二烯-苯乙烯塑料(ABS)。支架模型风洞试验在哈尔滨工业大学土木工程学院风洞与浪槽联合实验室中进行,大气边界层流场模拟为A类地貌风场,试验流场的参考风速主要通过TFI眼镜蛇三维脉动风速测量仪来测量和监控。数据测试采集系统由六分量高频测力天平、α角攻角变化机构、A/D转换器及数据采集处理用计算机等组成。四肢格构支架模型风洞试验及风向角示意如图6所示。

图6 四肢格构支架模型风洞试验及风向角示意
通过格构支架风洞试验获得均匀流风场下支架的广义位移值,同时利用Midas Civil软件计算得到格构支架在0°、45°和90°风向角下最大位移值,支架位移风洞试验值与有限元计算值对比见表5。

表5 支架位移风洞试验值与有限元计算值对比
由表5可以看出,四肢格构支架在均匀流风场作用下,风洞试验结果与有限元仿真分析存在一定误差,但最大误差为16.7%,在容许的范围内。试验结果表明:风洞试验能反映四肢格构支架的实际受力特性,同时可指导四肢格构支架实际施工,保障桥梁工程的安全施工。
7 结论
对台风区公路特大桥施工现场钢管格构支架体系进行有限元的静力分析,确保支架在最不利荷载工况下其强度能满足要求。将钢管格构支架格构柱部分简化为双向压弯构件,并对支架的稳定性进行计算,结果表明满足支架的稳定性要求。进一步对支架结构进行参数分析,考虑支架钢管直径、肢数、节段长度、支架总高度和纵横向间距等因素对支架结构临界荷载系数的影响,得出支架最优设计,经风洞试验及现场成功实践表明:
(1)当格构柱的壁厚δ与直径d的比值为定值时,其临界荷载系数会随着d的变大而迅速增长,相同情况下结构的δ/d越大,结构也越稳定。
(2)四肢钢管格构支架稳定能力较双肢和单肢的高很多,但是和六肢的承载能力相差不多,四肢钢管格构支架是最经济合理支架。
(3)当钢管格构支架总高度保持不变时,其节段高度越小,结构越稳定,但总高度不要超过70 m。当总高度大于70 m时,结构的稳定性维持在较低的水平。考虑到用料的经济性,其节段高度最大应不超过其设置联结系长度的3倍,可有效保证支架结构的稳定性。
(4)当支架的纵横向间距在5~7 m时,其稳定性呈现较快的上升趋势,间距在7 m附近达到峰值,当间距大于7 m时,支架稳定性随间距增大而降低。
(5)风洞试验能反映四肢格构支架的实际受力特性并指导工程实践,保障桥梁建设的安全性。

