极大线性无关组的计算复杂度*
魏其萍王 跃柳 彬
(1.贵州民族大学 数据科学与信息工程学院,贵州 贵阳 550025;2.贵州大学 数学与统计学院,贵州 贵阳 550025)
0 引言
极大线性无关组的个数,一般出现在代数问题中,而对于线性问题而言,这种问题一般转变到矩阵之上.矩阵产生于生活并在生活中发展,然而在矩阵中,矩阵的秩扮演着重要角色.通常来说,把矩阵看成是满足某些条件的向量按照一定的排列方法放在一起,其中给定的所有行向量(一般设其个数有限),如果在给出的极大线性无关组里面所含的向量是n个,则把这个n叫作是目标矩阵的行秩.[1]同样有列秩的说法.给出具体线性方程组,一般要问有无实际意义的解,而矩阵的秩正是判断的一种方法.向量空间中,矩阵扮演重要角色,因为矩阵的产生与向量空间中的向量有关,多个向量合在一起构成了向量组,它的线性相关与否这方面的理论,至今仍然是贯穿线性代数相关理论的主线.随着时代发展,在科学技术、天文地理、桥梁建筑等各个领域都涉及这类问题,当然有部分非线性的方程也能够近似或者直接化为线性问题来求解.[2]矩阵的秩仍然常常被用来判断对向量满足线性相关与否.因此,向量等矢量问题的极大线性无关组的数目在理论上具有实际意义.
1 求极大线性无关组的几种方法
如前所述,求极大线性无关组实际上都等价于求矩阵的秩.下面以求解矩阵的秩为例,说明求解的几种方法,并将在第二部分中对它们进行比较.
1.1 定义法
根据秩的定义,在一个给定的有限维矩阵中,行秩、列秩和秩相等,注意到是有限维,因此这个数目是确定的,并且这个数恰好就是行或列向量组中极大线性无关组的个数.在这样的前提之下,只要通过适当的方法计算得到矩阵行或列向量组的秩,我们便可以很方便地达到矩阵求秩的目标.因为行秩等于列秩.[3]换言之,行或者列向量的极大线性无关组如果有k个,那么k就是该矩阵的秩.
利用定义法求矩阵秩的步骤为:
(1)设矩阵A的行或列的向量组是α1,α2,…,αn.
(2)假设存在n数使得k1α1+k2α2+…+k nαn=0.
(3)根据α1,α2,…,αn的各个分量写出适当的方程组,并且显然要满足:
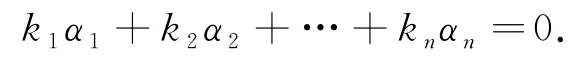
(4)解上述方程组.若存在非零解,则A的秩小于n.若只有零解,则A的秩为n.[4]
利用定义直接计算矩阵的秩,主要看行向量或列向量的线性相关的数目最多是多少,这种计算的方法类似于初等变换方法,但却与初等变换有实质性的差异,需要我们在运用中慢慢体会.
1.2 初等变换法
初等变换方法的原理是通过类似于解线性方程组中的加减消元法那样.初等变换之后,A变成等价阶梯形.阶梯形矩阵中,用行判断时整行的数值都不是0的那些行数目数就是该矩阵的秩,一般记r(A)为矩阵A的秩.当然用列判断的时候也类似.所谓的阶梯形矩阵,指的是将一个矩阵化成是具有上三角形或者下三角形内的数值全为零的形式.矩阵的初等行变换有如下3种:[1]
(1)互换行列式任意两行的位置,这样的做法仅仅改变矩阵子行列式的符号;
(2)将某一行的所有元素都乘以一个非零常数;
(3)将某一行的所有元素都乘以一个非零常数后,再加到另一行去.
只要将上述中的行改成列,便对应了初等列变换.在利用初等变换求矩阵的秩时,为了方便,总可以在作初等变换时把那些很方便观察的多个初等变换一次到位写出来.由于矩阵的秩在这样的变换之下还是同一个数,一般该数字在计算中不会出问题.
1.3 子式法
利用矩阵子式的方法寻找矩阵的秩,最主要的便要在矩阵的非零子式中,找出阶数最高的.按照子式定义的方法来看,所有子式不是零的里面阶数最高的那个,对应的阶数就是对应矩阵的秩.[5]因此首先要划分出矩阵的子式,然后在所有这些阶子式中找出非零子式的最高阶.
利用子式求秩,主要在能够观察的情况下运用,因为在一个矩阵中,它的子方阵很多,要计算诸多的子方阵的行列式,计算量是一个严重的问题.
1.4 特征值法
利用特征值法求矩阵的秩经常出现在方阵中,一般是将单位矩阵乘以一个未知的参数后与待求秩的矩阵作差,令作差后的矩阵行列式为零时解出非零参数.以n阶矩阵为例,未知参数可能有n个,此时令行列式为零时解出非零参数.如果有k个,则矩阵的秩为k.特别地,如果待求矩阵容易主对角化,那样很容易计算矩阵的秩.
利用特征值计算矩阵的秩,需要解行列式,因此在运用这种方法时,通常要求所求的矩阵是方阵,在方阵的前提下,才能够有行列式一说.特征值与矩阵之间的实际应用很广泛,特别在研究与矩阵相关的问题中,我们会遇到各种各样的矩阵和特征值问题.
2 几种方法的计算复杂度比较
2.1 不同方法求同一矩阵的秩
为了比较计算复杂度,我们分别用上述不同的方法求下面矩阵的秩:

注意,这里的矩阵为软件随机生成,若有雷同,纯属巧合.
解:方法1:利用初等行变换.对A进行初等变换得

显然,最终所获得的阶梯形矩阵中,不全为0的行数是4,从而可得出所求矩阵的秩为4;当然,也可以用初等列变换,同样能够得出A的秩为4;
方法2:利用子式.若存在四阶子式不为0,则A的秩为4.由行列式的初等变换可知

从而矩阵A的秩为4.事实上,方法一中我们施行的变换恰好也是行列式的初等变换;
方法3:利用定义求矩阵的秩.矩阵A的行向量组表示如下:

显然f(0)=-1≠0,这说明矩阵A没有0特征值,于是A的秩是4.
根据上述例子不难发现,对于同一个矩阵,利用初等变换、子式、定义以及特征值等4种方法都可以求出它的秩,但在求解过程中还是出现一定的差异.由于上述例子只是从4阶方阵来表述矩阵的秩,对计算复杂度的比较不是很明显,因此下面我们就这4种方法的适用范围和差异做简单介绍.下面仅仅从理论上说明计算的复杂度,不再用例子说明.
2.2 不同方法计算复杂度比较
在用初等变换的方法求秩时非常方便.对随即给出的有限维矩阵,总可以采用恰当的初等变换.经过有限次后就把原来的矩阵变到了一个阶梯形的.注意到矩阵的秩总是不随着变换而改变,再利用得到的阶梯形矩阵来对比判断目标矩阵的秩总是很有必要的,因为此时阶梯形矩阵的秩便是原矩阵的秩.另外,我们还可充分考虑其他问题,例如在施行初等变换把一个目标矩阵变成另一个阶梯形矩阵的过程中,为了节省时间和篇幅,可以多个初等变换同时进行,最终很快便可以获得想要的结果;当然,有时候可以将初等行与列变换混合使用以达到更方便有效地解决我们的目标问题的目的.

在利用定义来求矩阵的秩时,首先要明确该矩阵的行或列向量,利用向量是否线性相关来判断矩阵的秩是多少.在这个方法中,以n行m列的矩阵为例,通常利用n和m的最小值来计算,假设n≤m,我们则利用行向量是否线性相关来计算,便要定义n个未知数,但是解n元一次方程组也是比较棘手的过程,这个过程中稍不留神便会出现很大的错误.
在采取特征值方法时,求矩阵的秩也比较难.由于涉及矩阵的行列式计算,因此特征值方法一般只用于方阵中.如果方阵能够利用慧眼转变到主对角型,很方便的就可以求出目标矩阵的秩;如果方阵中零元素特别多,相对也比较容易计算.对于n阶方阵,如果其中的元素大多数都不为零,利用特征值方法时,单位矩阵的未知数倍与目标矩阵作差后的行列式也是n阶,要解这样的一个n阶行列式为零的未知数,一般来说难度系数特别大,因为在包括4阶及其以下的方阵中,求解未知数时总有计算公式,但大于或等于5阶时便没有公式可以遵循,因此当未知数为零时如果恒等式不成立,那么目标矩阵是满秩的,但当出现多重零根时便不好判断矩阵的秩是多少.
不难发现,对于行列数不大于4的矩阵而言,上述的4种方法在计算矩阵的秩时差异不是很大.但是对于行或者列中的最小数目比4更大时,初等变换方法适用于任意的矩阵,并且考虑到其他情况,如节省时间等等,计算矩阵的秩时可以同时实施很多个初等变换或者多步运算,并且初等行和列变换都可以混合使用以减少必要的步骤;子式判别法适用于稀疏矩阵,当矩阵的某几行或某几列能够直观表现出阶梯形时,便可以直接判定目标矩阵的秩不会小于某一个正整数,再计算大一阶的子式;根据秩的定义来计算矩阵的秩,需要解多元一次方程组,如果目标矩阵是稀疏矩阵,这种方法也非常实用;而在采用特征值方法计算矩阵的秩,一般要求目标矩阵是方阵,如果目标矩阵是稀疏的,也很容易求出非零特征值的个数.但出现多重零特征值时不好判断矩阵的秩是多少.
因此,对于求行列数更高的矩阵的秩时,利用初等变换更方便,对于n行m列且n≤m的矩阵,在多个初等行变换同时施行时,如果所有行第1个数不为零,第一步便可以将第2行到第n行的第1个数都化为零,即n-1个初等行变换同时进行,假设第2行第2个数不为零,那么第二步便可以n-2个初等行变换同时进行,将第3行到第n行的第2个数都化为零,……,以此下去,也特别容易将目标矩阵化为阶梯形.计算的时间复杂度约为

当用特征值方法判断时,作差时计算复杂度为n,n阶方阵的行列式复杂度为1,该行列式计算具有复杂度.采用行列式的定义时计算起来的时间复杂度约为

如果未知数表示的特征值为零时行列式成立,则说明矩阵不满秩,那么求解不为零的特征值的个数又将增加复杂度,甚至可能算不出来.
关于极大线性无关组的求解,以上我们利用等价描述求矩阵的秩来介绍最为基本的几种复杂度.而实际上关于极大线性无关组,求解方法远不止这些,建议读者研读文献[6-12],特别是线性规划和线性系统的最优控制问题方面,文献[8-12]给出了很多优化和计算方法,这些文献涉及一般的线性方程以及微分积分方程的控制系统,建议有兴趣的读者仔细研读,必将有所收获,此处不再一一介绍.
3 结语
综上所述,求解极大线性无关组虽然方法各异,不同的方法对应的计算复杂度差异相当大,以矩阵求秩为例,对于低阶矩阵,无论哪一种方法都很方便,但对于高阶矩阵而言,我们更愿意推荐利用初等变换的方法求矩阵的秩.本文主要以矩阵求秩为例对求解极大线性无关组的几种方法进行比较详细的说明和比较,理论与实际结合,初衷是为那些基础比较薄弱的学生提供矩阵分析和线性代数等基础方面的帮助,不当之处在所难免,望各位读者指正为谢!

