开州区百年一遇降水模型探讨
徐彦平 刘洁 韩世刚


摘 要:2019年我国部分地区出现异常降雨,多个地区出现了百年一遇的降雨,本文就如何理解“百年一遇”建立模型,以解释这一问题。根据重庆市开州区54a的年最大日降雨量画出降雨量的分布直方图,经过综合分析,选择出了气象降水常用的几种分布进行拟合,在K-S最优拟合检验下确定了Gamma、WBL、GEV 3种分布为开州区气候条件下的日降水极值分布函数模型,在此基础上又引入向量夹角θ参数,确定了GEV分布为最优模型。反演GEV模型参数时采用极大似然估计法,计算出的GEV模型参数为k=0.2058,α=79.9204,β=23.1998,由此得到了广义极值分布函数为F(Xi)=exp-[1+0.2058(Xi-79.920423.1998)]-10.2058(i=1,···,54),由F(Xi)函数得到重现期为Ta的降雨量R,并在概率统计的角度认为该降雨量为每年出现的概率为1T,与实际有一定差异,校正了气象理解Ta一遇降水的误区。
关键词:广义极值分布;极大似然估计法;K-S优度检验;向量夹角
中图分类号:S16 文献标识码:A
DOI:10.19754/j.nyyjs.20200430040
1 模型引言
2019年夏天,我国多个地区连降大雨、暴雨,有的地区出现了50a,甚至百年一遇的降雨,造成了严重的洪涝灾害,给一些地区带来了巨大的财产与经济损失。
开州区地处渝东北山区,是川东有名的暴雨中心,1957—2005年共出现暴雨日数227d。其中,日降水量大于100mm的有31d,大于150mm的有4d,大于200mm的有2d。2004年9月5日的日降水量达295.3mm,堪称“百年一遇”的降水,特大降雨引发的自然灾害给开州区造成了重大经济损失,有必要研究特大强降雨过程重现周期和20a、40a、60a、80a、100a内的最大预测降水量。
2 模型假设
自动气象站记录的日最大降雨量数据属于自然降雨量,不考虑人工影响天气等人为因素降雨量。
所统计的1a中日最大降雨量与真实值符合,没有出现漏记、改动等意外情况。
日最大降雨量不受季节气象因素的影响。
3 符号说明
4 模型建立与求解
本题中的“百年一遇”的日降雨量R并非100a就出现1次,其是一个概率概念,假如以年为计时单位,通过总结以前所记录的数据规律可知,1a中日降雨量最大值Ri服从一种概率分布,而R出现的概率非常小,仅为0.01,因此说R为“百年一遇”,如果在丰雨年,R有可能不止出现一次,而并非100a才出现1次。据统计,重庆市开州区1957—2010年54a中日最大降雨量Ri的数据见表2。
由这些数据用Matlab软件画出日极大降水量的频率分布直方图,并结合直方图特点选择出气象雨量分布常用的分布函数Gamma分布,Normal分布,Weibull分布,Extreme Value分布,Exponential分布,Generalized Extreme Value分布进行拟合,拟合图见图1~6。
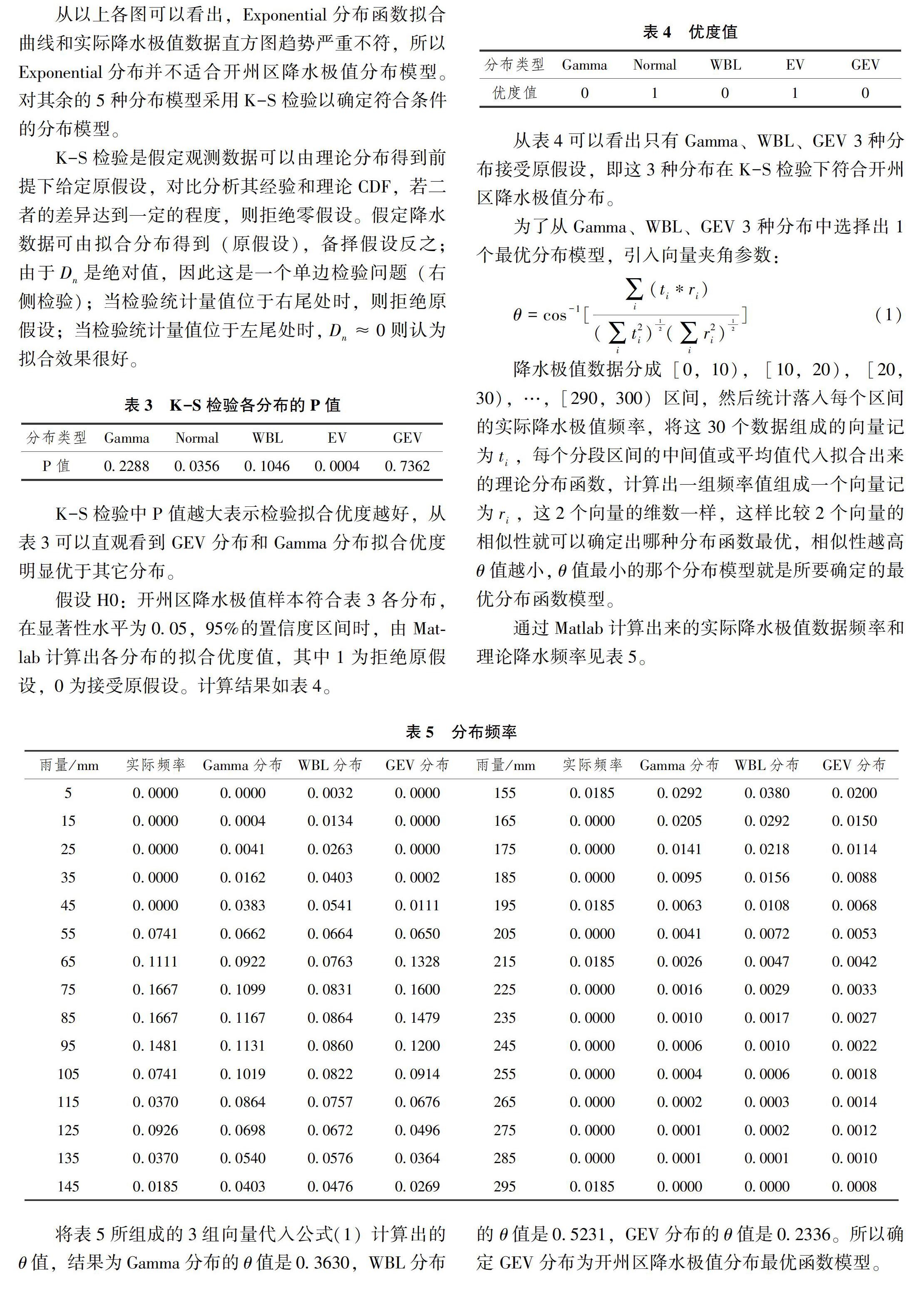
从以上各图可以看出,Exponential分布函数拟合曲线和实际降水极值数据直方图趋势严重不符,所以Exponential分布并不适合开州区降水极值分布模型。对其余的5种分布模型采用K-S检验以确定符合条件的分布模型。
K-S检验是假定观測数据可以由理论分布得到前提下给定原假设,对比分析其经验和理论CDF,若二者的差异达到一定的程度,则拒绝零假设。假定降水数据可由拟合分布得到(原假设),备择假设反之;由于Dn是绝对值,因此这是一个单边检验问题(右侧检验);当检验统计量值位于右尾处时,则拒绝原假设;当检验统计量值位于左尾处时,Dn≈0则认为拟合效果很好。
K-S检验中P值越大表示检验拟合优度越好,从表3可以直观看到GEV分布和Gamma分布拟合优度明显优于其它分布。
假设H0:开州区降水极值样本符合表3各分布,在显著性水平为0.05,95%的置信度区间时,由Matlab计算出各分布的拟合优度值,其中1为拒绝原假设,0为接受原假设。计算结果如表4。
当T=100时,也就是说降雨量R=257.7364mm的重现期为100a,这个降雨量也就是气象预报中所说的“百年一遇”的降雨量。但事实并不能按照其字面意思理解,这里的“百年一遇”,并不是100a才出现1次,只是根据极值降雨量的分布规律,可以得出降雨量服从广义极值分布,在这种概率分布下,降雨量R=257.7364mm出现的概率为0.01,在气候稳定的条件下,这一降雨量一般不容易出现,理论上有可能100a才出现1次。但实际情况并非如此,若在丰雨年,其有可能在1a中多次出现,也有可能多年连续出现,随着现在气候的异常变化,这种情况有可能出现更为异常的变化。
因此,如果不清楚这种理论,就有可能误解“百年一遇”这一概念,认为这一降雨量真的是100a才出现1次。另外,在气象预报中用这种概念,也有误导人的嫌疑。
5 模型的评价与推广
本文的模型在建立时,采用了开州区气象局采集的从1957—2010年54a日降水量极值数据,保证了数据的真实性与可靠性;同时也确保了所建立的模型与实际情况相符合;本文中所建立的模型能够解决题目所提出的问题,可以帮助人们理解有关这一类的问题。同时,模型也存在不足之处,如所用的数据只有54组,因此在拟合的时候,有可能会因为数据的不足而使精确度下降。
由于GEV参数估计时所用的数据是开州区54a日降雨量极值,所以导出的模型分布函数包含了开州区气候条件因素,代表了开州区降水量极值的趋势,计算Ta一遇降水极值问题时将T赋值为相应的数值代入公式6即可预测出极值日降水量。
但是由于开州区数据样本量较少,所以计算Ta一遇降水极值时T值不应过大,即T值有一个范围,这个范围应该根据气候的稳定条件来定,如果气候条件稳定,那么T值可以相应的取大一些。本文中T最大值取到100是合理的,在气象中气候属于大尺度模式,其比较稳定,短时期内不会发生大的变化,在置信水平为0.05条件下模型是合理的。如果T值取的很大,模型的合理性就不能保证,因为不能保证1000a以后的气候模式和现在会有怎样的不同,所以用54a的数据反演的分布函数模型预测1000a的降水量极值显然不能保证预测值的合理性,但反过来用1000a的数据反演的函数模型预测54a的降水量极值,预测值是可靠的。
当积累的数据量极值数据变得多时,应该使用更多的数据样本对模型参数进行反演以提高模型精度,数据样本越多T的有效值也将越大。此模型只在开州区气候模式下适用,如果换成其它气候模式需要相应的样本数据对分布函数参数进行反演,而且其它气候模式条件下的样本数据最优分布函数不一定为GEV分布,对具体的气候模式要选择对应的最优函数分布。
参考文献
[1] 王海军,张峻,王宏记,等.长江三峡地区宜昌、巴东短历时极值降水特征分析[J].暴雨灾害,2010,29(1):38-43.
[2]张婷,魏凤英.华南地区汛期极端降水的概率分布特征[J].气象学报,2009,67(3):442-451.
[3]盛骤,谢式千,潘承毅.概率论与数理统计[M].第4版.北京:高等教育出版社,2008.
(责任编辑 常阳阳)

