Effect of near-neighbor interaction on magnetization of hybrid spin Blume-Capel model

LI Xiao-Jie, CAI Xiu-Guo, XIN Miao-Miao

(Qilu Institute of Technology, Jinan 250200, China)

Abstract: The effect of the exchange interaction between the nearest neighbor atoms on the nanotubes on the magnetization of lattice points in the Blume-Capel model was studied by using the effective field theory.The results show that the nearest neighbor exchange interaction and the strength of crystal field compete with each other, which makes the system show rich magnetic characteristics.When the negative crystal field acts on the system, the first order phase transition occurs.The magnetization of the system is remarkably different when the parameters of the crystal field and the exchange interaction are different.

Key words: Near-neighbor interaction; Magnetization; Blume-Capel model; Nanotube; Effective field theory.

1 Introduction

Since theBlume-Capel (BC) model was established in 1966[1,2], the magnetization properties, thermodynamic properties and phase diagrams of BC models on a variety of lattices have been studied using different methods.Zhang and Yan studied the phase transition behavior of a mixed spin system in a simple cubic lattice when the external magnetic field follows a three-mode random distribution[3].In the same year, Zhang and Yan also studied the critical behavior of a mixed spin system in a simple cubic lattice when both the external magnetic field and the exchange interaction follow a bimodal random distribution[4].The compensation behavior and magnetization process of BC model in simple cubic lattice were studied by using the effective field theory[5].The phase transition properties of honeycomb lattice when the external magnetic field obeying the bimodal discrete distribution were studied, and it was found that the exchange interaction among the external magnetic field, crystal field and spin affected the phase transition of the system and the system reentered[6].The research shows that the diluted crystal field has an effect on the magnetic properties and phase transition of the honeycomb lattice system[7].The results show that when the crystal field meets the dilution distribution, it has no effect on the phase transition of the system and the system will not show the three-critical phenomenon.In recent years, nanotubes have gradually become a hot topic in the field of magnetic properties research.In the experiment, Maoruietal.prepared SnO2nanotube materials using plant cellulose as the template.The test results showed that this SnO2nanotube material could improve the diffusion rate of lithium ions and effectively solve the problem of the expansion of electrode materials during charging and discharging[8].It is found that magnetic nanotubes have obvious anisotropy[9].Theoretically, Zaim group studied the phase diagram and magnetic properties of 1 Ising model on the nanotube with external magnetic field consistent with three-mode distribution[10].The results showed that the system was proved to have first-order phase transition, three-phase critical point and second-order phase transition, and re-entrant phenomenon was observed.Osmanetal.respectively discussed the magnetic properties and critical phenomena of the pure spin system and the mixed spin system in the nanotubes[11-13], and discussed the influence of crystal field on the magnetic properties of the system.The results showed that there were first-order phase transitions and second-order phase transitions in the system.Kaneyoshi discussed the variation of the magnetization rate with temperature in the nanotubes[14], and found that the magnetization rate of the system will be changed when the interaction between the outer shell and the inner shell's nearest neighbor spins is different.The results of Lietal.[15]showed the magnetization and phase transition properties of BC model in the double-mode random crystal field, and obtained the relationship between the magnetization of the system and the temperature and the random crystal field, as well as the phase diagram.The results showed that the system would show different magnetic properties and phase transition behaviors in diluted crystal field, staggered crystal field and homogeneous crystal field.The thermodynamic and phase change properties of BEG model on nanotubes were discussed[16].Lietal.[17]studied the magnetization properties of BC model in nanotubes under the action of diluting crystal field, and the results showed that the internal energy, specific heat and free energy of the system under the action of diluting crystal field presented different magnetic properties.The first-principles method based on density functional theory was used to study the hydrogen storage performance of rare earth metal La adsorption doped BN nanotubes[18].As far as we know, the effect of the spin exchange interaction between the nearest neighbor atoms on the magnetic properties of the magnetic nanotube system has not been discussed.To figure out the nearest-neighbor exchange interaction on nanotubes magnetic thermal properties of the system, in this paper, by using effective field theory of nanotubes on BC magnetization and thermodynamic properties of lattice model and exchange interaction, the relationship between temperature and the crystal field strength are studied, nanotubes lattice of magnetization is given and the change of the thermodynamic properties with temperature curve.

2 Theoretical methods

The schematic picture of an infinite cylindrical Ising nanotube is illustrated in Fig.1(a).It consists of a surface shell and a core shell.Its cross section is presented in Fig.1(b).Each point in Fig.1 is occupied by a spin-1 Ising magnetic atom.Here, only the nearest neighbor interactions were considered.The exchange couplings between two magnetic atoms were represented by solid bonds, which were plotted between Fig.1(a) and (b).To distinguish the atoms with different coordination numbers, circles, squares and triangles were used to describe different atoms.

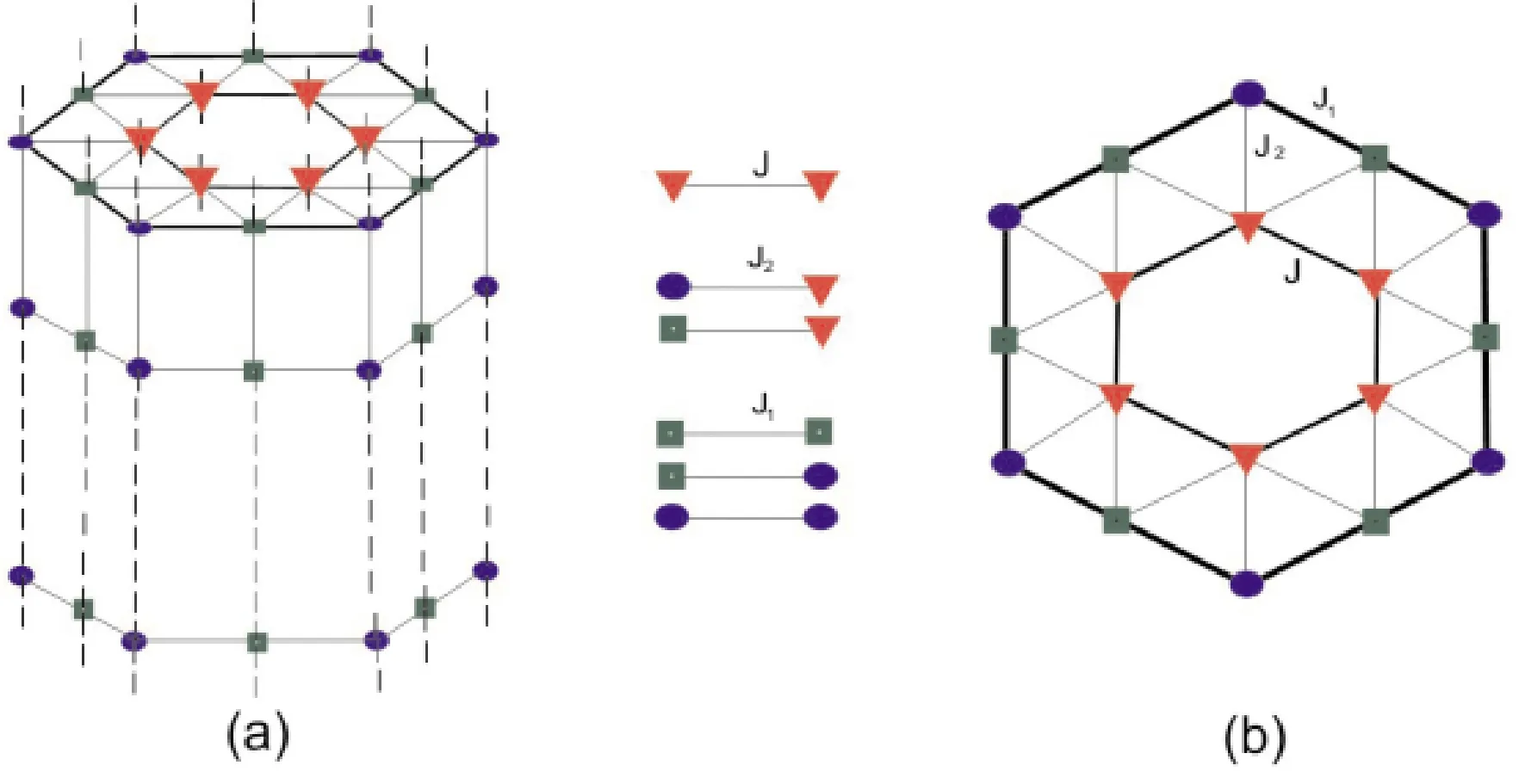
Fig.1 Shows a schematic diagram of the nanotubes.Fig.(a) represents the stereogram and fig.(b) its transverse section.The blue circles and green squares represent the magnetic atoms in the outer shell, the red triangle represents the magnetic atoms in the inner shell, and the solid lines represent the exchange interactions between the nearest neighbor atoms.

The Hamiltonian of a cylindrical nanotube is expressed as

(1)

whereSis the Ising operator and the spin might take the values S = ±1, 0.J1is the exchange interaction between two nearest-neighbor magnetic atoms at the surface shell andJis the exchange interaction in the core shell.J2is the exchange interaction between atoms at the surface and the core shell.handDrespectively represent the external magnetic field and crystal field intensity acting on the lattice points.

It can be obtained the longitudinal magnetizationsm1, m2at the surface shell and mcat the core shell for the nanotube within the framework of the EFT[19-21]：

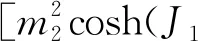
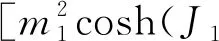
(2a)

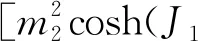
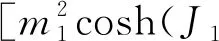
(2b)

(2c)

Here, the function F (x) is defined by as follows:

(3)

Whereβ=1/kBT,Tis the absolute temperature andkBis the Boltzmann factor.Furthermore, let us define the total longitudinal magnetization of per site as follow:

(4)

3 Results and discussion

For the convenience of following discussions, we defined the reduced parameters asJ1/J,J2/JandD/J.In the paper, we studyJ1/J=0.001, 0.5 andJ2/J= 0.001, 0.5.The magnetization curves which were obtained numerically by solving Eqs.(2a)-(2c) were plotted.

Fig.2 shows the variation curves of the spin magnetization intensity and the spin magnetization intensity of the inner shell lattice point and the system average magnetization intensity with temperature whenJ1/J=0.001 and the crystal field intensity parameterD/Jis different.It can be seen from the figure that when the interaction intensity between the spin of the outer most neighboring atom is small, the magnetization intensity of the system presents differences under the action of different crystal field intensities.At the same temperature, the stronger the negative crystal field is, the smaller the system magnetization is, and the lower the phase transition temperature is when the second-order phase transition occurs.The comparison between Fig.2(a) and Fig.2(b) shows that the positive crystal field has a promoting effect on the magnetization intensity of the system, but the variation trend with temperature is similar with without the effect of crystal field.When the negative crystal field acts on the system, the magnetization intensity of the system is significantly different, as shown in Fig.2(c)-(i).It can be seen from the figure that the negative crystal field can inhibit the magnetization of the system.Fig.2(c) shows that when the negative crystal field intensity is small, the ground statem1=m2=MT=1.With the increase of the negative crystal field intensity, both the spin magnetization intensity and the spin magnetization intensity of the shell lattice point are less than 1 or even become 0 in the ground state, but the spin magnetization intensity of the inner shell lattice point remains unchanged in the ground state,mc=0.5, as shown in Fig.2(d)-(g).This is because the spin of the shell lattice point is 1, while the spin of the inner shell lattice point is 1/2.With the enhancement of the negative crystal field, the state where the spin of the shell lattice point is equal to 1 will jump to the state where the spin is 0, but the inner shell lattice point has only S=±1/2.As the intensity of negative crystal field continues to increase, the magnetization intensity of shell lattice points tends to 0, as shown in figure 2(h) and (I).

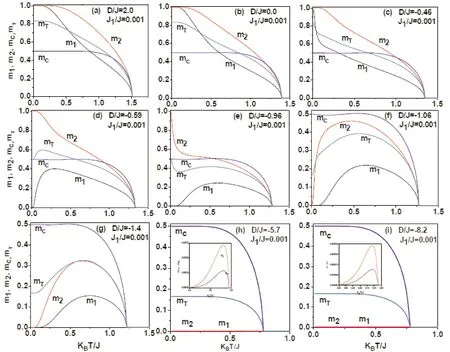
Fig.2 The temperature dependence of the magnetization is presented with J1/J=0.001.

Fig.3 shows the variation curve of the spin magnetization intensity and the spin magnetization intensity of the inner shell lattice point and the system average magnetization intensity with temperature whenJ1/J=0.5 and the crystal field intensity parameterD/Jis different.It can be seen from the figure that the system has a first-order phase transition and a second-order phase transition.Compared with Fig.2 and Fig.3 shows that the variation trend of system magnetization with temperature is the same under the action of orthomorphic field and without the action of crystal field, but the temperature at which the second-order phase transition occurs in the system is relatively high, indicating that the near-neighbor exchange interaction can affect the magnetization intensity of the system.When the crystal field is -1.72, the system will undergo a first-order phase transition, as shown in Fig.3(e).As the negative crystal field intensity continues to increase, the first-order phase transition of the system disappears and the magnetization intensity of the shell lattice points all becomes 0, as shown in Fig.3(f).

Fig.4 shows that whenJ2/J=0.001, the system magnetization shows rich magnetization characteristics.Under certain conditions, the spin magnetization intensity and the variation trend with temperature of the shell lattice point are exactly the same, and only second-order phase transition occurs in the system, as shown in Fig.4(a)-(b).As the intensity of negative crystal field increases, the magnetization intensity of the lattice points of the outer shell exhibits a first-order phase transition, as shown in Fig.4(c)-(e).When the negative crystal field is strong enough, the first-order phase transition of the system disappears and only the second-order phase transition occurs, as shown in Fig.4(f).

Fig.5 shows that whenJ2/J=0.5, only second-order phase transition occurs in the system, but the spin magnetization intensity of shell lattice points has a similar change trend with temperature.Fig.5(c)-(f) shows that when the negative crystal field ACTS on the system, the system shows abundant magnetization characteristics, and the system's magnetization intensity shows extraordinary heterogeneity with the change of temperature.

Fig.3 The temperature dependence of the magnetization is presented with J1/J=0.5.

Fig.4 The temperature dependence of the magnetization is presented with J2/J=0.001.

Fig.5 The temperature dependence of the magnetization is presented with J2/J=0.5.

4 Conclusions

The effect of the spin exchange interaction between the nearest neighbor atoms on the magnetization of the BC model in the nanotube system was studied by using the effective field theory.The results show thatspin magnetization of shell lattice points and the spin magnetization of the inner shell lattice point are closely related to the nearest neighbor exchange interaction.Exchange interaction and crystal field strength and many other factors compete with each other, which will make the system show more abundant magnetization properties: there are first-order phase changes and second-order phase changes in the system lattice point magnetization curve with the change of temperature.