原子尺寸对Lennard-Jones液体玻璃转变过程中动力学不均匀性的影响

王智聪, 孙永丽, 幸晓凤

(太原理工大学 物理与光电工程学院, 太原030024)

1 引 言

当冷却速度足够快, 液体可避免结晶而在过冷至低于某一温度(玻璃转变温度)时, 内部原子大规模的运动在时间尺度上被冻结, 从而形成非晶结构[1,2].玻璃是一种典型的非晶态材料, 人类发现玻璃到应用玻璃已经有近千年, 但其转变机制仍然是凝聚态物理的难题之一[3-5].许多关于玻璃转变的理论模型, 如自由体积模型[6]、 热力学统计模型[7]、 能量势垒理论[8]、 固体模型理论和模态耦合理论[9,10]等等, 并不能完整而明确地解释玻璃转变现象.玻璃态的原子结构和其动力学性质是密不可分的, 玻璃态形成过程中, 其原子结构的变化必然会引起其动力学性质的显著变化.目前的相关研究[11-14]多是关于对扩散系数D、 非高斯参数α2(t)、 粘度η等动力学性质随时间变化趋势的研究, 也有压强对非晶体结构和动力学性能的研究[15,16], 原子尺寸与动力学性质的关系并未过多涉及.本文研究了原子尺寸对LJ液体玻璃转变过程中动力学性质的影响.

2 模拟研究的条件和方法

本文采用Lammps经典分子动力学软件[17]进行模拟.初始状态为8781个A原子和2195个B原子随机排列而成的立方原胞, 约化单位下A, B的质量均为1.采用周期性边界条件和等温等压(NPT)系综, 使用LJ势[18], 势函数为

(1)

其中α,β∈{A, B}, 相互作用势参数σ和ε分别为长度和能量单位.对于氩, 其对应的长度为3.41Å, 能量为120KkB.设置势函数参数如下:εAA= 1.0,εBB= 0.5,εAB= 1.5,σBB= 1.0,σAB=(σAA+σBB) / 2, 这与文献[19, 20]中所研究的参数ε相同.设置σAA分别为0.9、 0.86、 0.82和0.78进行模拟.初始温度为T*= 0.9, 对应于T= 109 K, 时间步长为0.01 ps, 具体模拟过程为: 初始结构在温度为0.9时弛豫足够的时间确保体系达到平衡, 之后采用梯度降温法以1.88×1012K/s的冷却速率每隔0.05降温至0.3, 每降温一次平衡一次并输出相关数据以供后续分析使用.

3 模拟计算结果与分析

3.1 玻璃转变温度Tg分析

冷却过程中, 原子尺寸不同的体系平均原子体积随温度的变化曲线的斜率是连续的, 并没有出现突变, 如图1, 这是由于降温速率较快, 原子重组速度较慢,无法在冷却条件限定的时间内完成充分重组.此时, 液态的结构好像被“冻住” ,从而发生玻璃转变形成非晶结构.玻璃转变温度Tg是判断液体非晶形成能力的重要依据[21].通过体积判别法[22,23]能够得到原子尺寸为0.9、 0.86、 0.82、 0.78时所对应的Tg的值分别为0.6037、 0.5904、 0.5808、 0.5772, 在所研究尺寸范围内Tg随原子尺寸的减小而减小.

图1 不同原子尺寸下LJ体系平均原子体积随温度的变化关系Fig.1 Relationships between average atomic volume and temperature of LJ system under different atomic sizes

图2 (a) σAA= 0.9时不同温度下MSD随时间的变化; (b)T*= 0.45时不同原子尺寸下体系的MSD随时间的变化Fig.2 (a) The MSD of LJ system at different temperatures when σAA= 0.9; (b) The MSD of LJ system with atomic sizes of 0.78 - 0.9 when T*= 0.45

3.2 均方位移MSD分析

均方位移MSD是用来描述体系中的原子在时间t内平均位移的平方, 通过计算MSD来研究原子尺寸对体系动力学性质的影响.图2(a)是尺寸为0.9时不同温度下MSD随时间的变化.在高温阶段, MSD对时间呈线性关系, 此时体系为液态.随着温度的不断下降, MSD逐渐出现平台区且越来越明显, 说明原子运动受到的束缚越来越大.t< 0.2 ps, MSD随时间的增加很快, 原子受到的束缚较小做自由振动.0.2 10 ps, MSD随时间增加较快, 原子脱离笼子的束缚做长程扩散运动, MSD斜率随温度的下降而不断减小, 粒子运动越来越慢, 动力学不均匀性越来越强.图2(b)为温度0.45时原子尺寸不同的体系的MSD随时间的变化, 在自由振动阶段, MSD几乎重合, 说明原子尺寸对做自由振动的原子影响微乎其微; 在长程扩散阶段,尺寸越小, 原子扩散受到的限制越大; 在β弛豫阶段, 原子尺寸大的体系MSD高于尺寸小的体系, 说明尺寸越小, 原子之间的相互作用力越强, 动力学不均匀性越强.

3.3 扩散系数D分析

通过对MSD曲线求斜率可以得到不同原子尺寸下体系的扩散系数D, 图3为lnD随1/T*的变化关系, 可以得到原子尺寸越小扩散系数D越小.在高温阶段,不同尺寸下体系lnD与1/T*的关系均可以用Arrhenius方程[25]表示, 即

图3 不同原子尺寸下体系的扩散系数D随温度的变化及拟合曲线Fig.3 The variation of diffusion coefficient D with temperature under different atomic sizes and fitting curves

(2)

其中,D0为指前因子,E为扩散激活能,KB为玻尔兹曼常数,T*为温度.通过拟合得到不同尺寸下的D0分别为6.07、 6.37、 6.91、 6.93;E分别3.19 KB、3.29 KB、 3.41 KB、 3.46 KB, 即原子尺寸越小, 跃迁过程中克服周围原子对其阻碍所需要的扩散激活能越大.当温度低于0.6附近时, 扩散规律逐渐偏离高温时的规律, 这表明在降温过程中, 整个体系的微观结构随温度发生了改变, 使得其动力学性质发生不连续变化.

3.4 非高斯参数α2(t)

非高斯参数α2(t)是用来表征动力学不均匀性的重要方法, 其峰值αmax表示动力学不均匀程度.图4为四种原子尺寸不同的体系分别对应的不同温度下非高斯参数α2(t)随时间的变化关系, 由此得出四种体系中, 当t< 0.2 ps, α2(t) = 0, 原子运动在振动阶段符合高斯分布; 当0.2 τβ, 体系进入α弛豫阶段, 温度较高时的非高斯参数α2(t)不断减小直到趋于零, 表明原子扩散动态特性满足高斯分布, 温度较低时的非高斯参数α2(t)未减小到零, 这是由于低温时体系的弛豫时间不够充分.同时, 经过拟合四种体系β弛豫中不同温度下非高斯参数α2(t)随时间的变化趋势, 得到四种体系的非高斯参数α2(t)与时间t的关系均满足幂律函数[26]:

α2(t)=α0×(t-t0)γ

(3)

其中指前因子α0分别为0.155、 0.177、 0.204、 0.212,β弛豫开始时刻t0= 0.2,指数γ分别为0.556、 0.577、 0.559、 0.609.图5是四种体系不同温度下的非高斯参数峰值αmax统计图, 随着温度下降, 粒子运动变慢, 动力学不均匀性增强, 低温时原子尺寸越小, 原子之间的引力越强, 体系的动力学不均匀性越强.

3.5 粘度η分析

液体粘度是决定其玻璃形成能力的关键动力学参数, 因此计算体系粘度对研究玻璃转变过程中动力学性质的变化至关重要.

根据Green-Kubo公式[27], 即

(4)

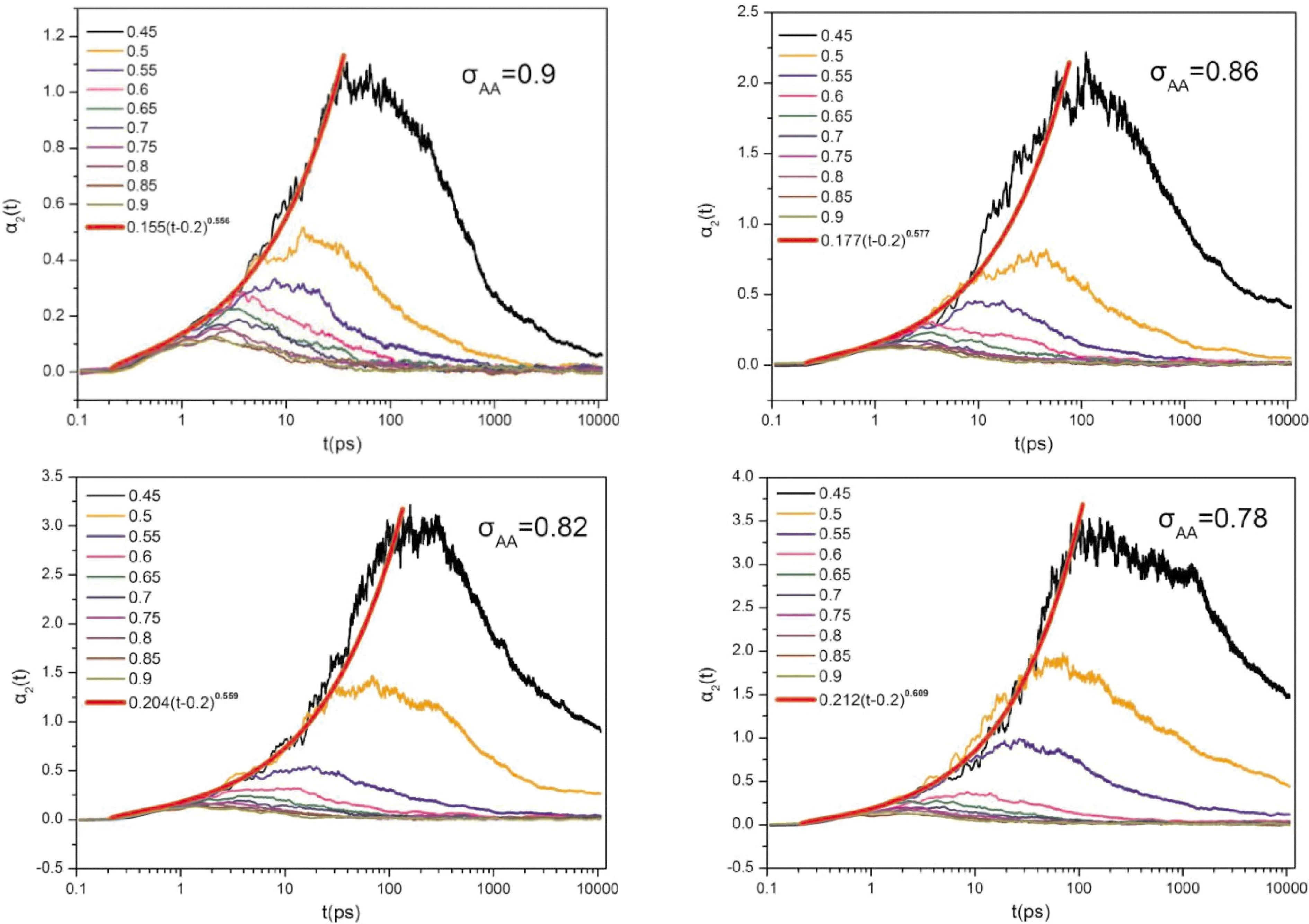
图4 不同原子尺寸下不同温度的非高斯参数α2(t)随时间的变化及拟合曲线Fig.4 The variation of non-Gaussian parameter α2(t) with time at different temperatures under different atomic sizes and fitting curves

图5 不同原子尺寸下非高斯参数峰值αmax随温度的变化Fig.5 The peak values of non-Gaussian parameter αmax at different temperatures under different atomic sizes

其中,V是系统体积,KB是玻尔兹曼常数,Pxy是压力张量的偏对角线分量, 〈…〉是求系综平均.压力张量表达式为

(5)

η=η0exp[D*T0/(T-T0)]

(6)

其中,η0是温度趋于无穷大时的粘度值,T0是粘度趋于无穷大时的温度值, D*代表动力学强度, 是衡量液体脆性的指标.四种不同体系的粘度值均随温度的下降而增大并在各自的玻璃转变点(Tg)附近发生突变[29], 尺寸越小的体系的粘度值越大且突变越明显，其动力学不均匀性越强.

图6 不同原子尺寸下粘度η随温度的变化及拟合曲线Fig.6 The variation of viscosity η with temperature under different atomic sizes and fitting curves

4 结 论

本文基于Lammps分子动力学软件, 研究了原子尺寸对LJ液体玻璃转变过程中动力学性质的影响, 得到如下结论:

(1)在研究范围内, 四种原子尺寸不同的体系快速冷却凝固均形成非晶体, 且玻璃转变温度Tg和体系的扩散系数D均随着原子尺寸的减小而减小.研究均方位移MSD得到在β弛豫阶段原子尺寸越小, 体系动力学不均匀性越强, 体系温度越低, MSD斜率越小, 即整个降温过程中, 体系动力学性质发生了不连续变化.

(2)β弛豫阶段非高斯参数α2(t)随时间的变化关系符合幂律函数, 与原子尺寸大小无关.非高斯参数峰值随温度的降低以及原子尺寸的减小而不断增加, 并随着温度的降低向长时间区域移动, 证实了玻璃转变过程中动力学不均匀性的存在以及不均匀性程度与温度和原子尺寸大小有关.

(3)对体系粘度的计算发现LJ液体粘度与温度和体系内原子尺寸大小紧密相关, 粘度随着温度的降低及粒子尺寸的减小而增大, 与非高斯参数峰值随温度及原子尺寸大小的变化趋势相同, 即体系的动力学不均匀性随着原子尺寸的减小而增大.