新型稀磁半导体Fe掺杂LiZnP的光电性质

杜颖妍， 杜成旭， 贾 倩， 陈 婷， 刘 焦， 于 越， 张恒源， 刘 明， 毋志民

(重庆师范大学 物理与电子工程学院 光电功能材料重庆市重点实验室， 重庆 401331)

1 引 言

近年来，稀磁半导体 (Diluted Magnetic Semiconductor, DMS)由于其在自旋电子学上的潜在应用引起了人们的广泛关注，它将微观电子学与自旋相互作用结合，可以兼具半导体和磁性材料的性质，使得同时利用电荷自由度和自旋自由度成为可能[1, 2].但是，传统稀磁半导体出现了两点不足[3,4].首先，在引入自旋的同时也引入了载流子，这种自旋和电荷的捆绑效应严重制约了自旋和电荷的调控维度；其次，基于Ⅲ-Ⅴ族DMS的不等价代替导致磁性离子化学固溶度严重受限，Mn的平均固溶度不足1%，仅可形成亚稳态薄膜材料，材料的质量严重依赖于制备方法并对热处理过程有较高的敏感性.

为克服上述困难，Mašek等人[5]在理论上提出了基于I-II-V族的新型稀磁半导体Li(Zn,Mn)As，将(Ga,Mn)As中III族的Ga替换为I族的Li和II族的Zn，计算发现电荷和自旋的浓度可分别通过Li的化学计量数和Mn的含量来调控，Mn2+占据Zn2+位，等价掺杂使得Mn在该化合物中具有高的固溶度.实验上，靳常青研究组[6-8]成功制备了多晶Li1+y(Zn1-xMnx)As块体材料，发现母体材料表现为抗磁性，Mn掺杂后，Li不足(VLi)时样品表现出顺磁性，而当Li过量(y≥0.05)时，样品则变为铁磁性，并随着Mn浓度的增加，居里温度(TC)逐渐提高，但是，Li(Zn,Mn)As的TC仍低于室温，最高只有50 K.尽管如此，Li(Zn,Mn)As体系为寻找新的自旋电子学材料提供了契机.Pang等人[9]通过第一性原理计算对Mn掺杂LiCaP的磁性进行了研究，发现当Li过量时材料的导电性增加；Li不足时，体系的TC提高.Deng等人[10]采用自旋和电荷分离掺杂的方法成功地合成了块状稀磁半导体Li(Zn,Mn)P，研究表明其是一种软磁性材料，可以通过提高体系的载流子浓度来提高TC.顾[11]通过对Fe掺杂ZnO稀磁半导体磁性能的研究，发现Zn1-xFexO样品都表现出明显的铁磁性，且磁性随着Fe掺杂浓度的增大而升高.Zhang等人[12]采用水热法成功制备了Fe掺杂ZnO多晶样品，Fe离子替代Zn离子引入磁性，样品表现出明显的室温铁磁性.

开发性能优异的磁电分离调控的新型稀磁半导体是新一代自旋电子器件的关键，Fe掺杂[11,12]在上述材料中已经展现了良好的性质，母体材料LiZnP带隙大，理论表明，稀磁半导体中载流子自旋与局域自旋间的交换积分(Jp-d)会随着半导体能隙的增大和晶格参数的减小而增加[13]，更大的交换积分也意味着更高的居里温度.基于此，本文采用基于密度泛函理论(Density Functional Theory, DFT)的第一性原理计算方法[14]对新型稀磁半导体Fe掺杂LiZnP体系进行研究.我们采用平面波超软赝势法(Plane-Wave Pesudopotential, PWP)[15]，对48原子超晶胞体系进行几何结构优化，计算并分析了体系的电子结构、形成能、居里温度和光学性质.对自旋和电荷分离调控的Li(Zn,Fe)P体系的研究有助于理解磁性机理，将为进一步的实验研究提供有意义的参考.

2 模型结构与计算方法

2.1 模型构建

LiZnP的晶体结构与LiZnAs相同[16,17]，为面心立方结构，空间群为F-43m，晶格常数a=b=c=0.5765 nm.构建模型时，可以将LiZnP看作是[ZnP]-型的闪锌矿结构，然后Li原子填充在其间隙位置上[10].原子排列方式为，Zn原子位于τ1=(0,0,0)a，P原子位于τ2=(1/4, 1/4, 1/4)a，Li原子填充在间隙位置τ3=(1/2, 1/2, 1/2)a处.LiZnP是一种带隙值为2.04 eV的直接带隙半导体，可以通过Li，Zn，P的单质经固相反应法合成[18].如图1所示，计算基于含48个原子的2×2×1超晶胞体系，掺杂时，用一个Fe原子替代一个Zn原子，而Li空位和Li填隙则是分别去掉和添加一个Li原子，为了寻找最稳定的结构，分别选取了Fe周围沿晶格a，b，c方向上三个不等价的位置，对应到超晶胞模型图1(a)中的VLi1，VLi2，VLi3和(b)中的ILi1，ILi2，ILi3.优化计算发现VLi2和ILi1位置最稳定，因此本文选取这两种结构计算Fe掺杂后Li空位和Li填隙的性质.

图1 Li1±y(Zn1-xFex)P的48原子超晶胞结构图.(a) Li1-y(Zn1-xFex)P; (b) Li1+y(Zn1-xFex)P Fig.1 Supercell structures of Li1±y(Zn1-xFex)P with 48 atoms.(a) Li1-y(Zn1-xFex)P; (b) Li1+y(Zn1-xFex)P

2.2 计算方法

计算是由基于密度泛函理论的量子力学程序CASTEP[19]完成，采用周期性边界条件，利用局域自旋密度近似(Located Spin Density Approximation, LSDA)处理电子间的交换关联能，各元素的价电子构型分别为Li:1s22s1、Zn:3d104s2、P:3s23p3、Fe:3d64s2.在倒易的K空间中，计算选取的截断能Ecut为520 eV.体系总能和电荷密度在对布里渊区(Brillouin)的积分计算采用Monkhorst-Park[20]方案，K网格点选取为6×6×5，其自洽收敛精度为2.0×10-6eV/atom.结构优化中采用BFGS[21]算法优化，其原子间相互作用力收敛标准为0.2 eV，单原子能量收敛标准为1.0×10-5eV/atom，晶体内应力收敛标准为0.05 GPa，原子的最大位移收敛标准为1.0×10-4nm.为使计算结果更加精确，计算中先优化晶胞结构，根据所得晶胞参数再优化内坐标.本文首先计算了掺杂体系的形成能Ef[22]，以研究其结构的稳定性

Ef=E[Li1±y(Zn1-xFex)P]-E[LiZnP]-

nFeμFe+nZnμZn±nLiμLi

(1)

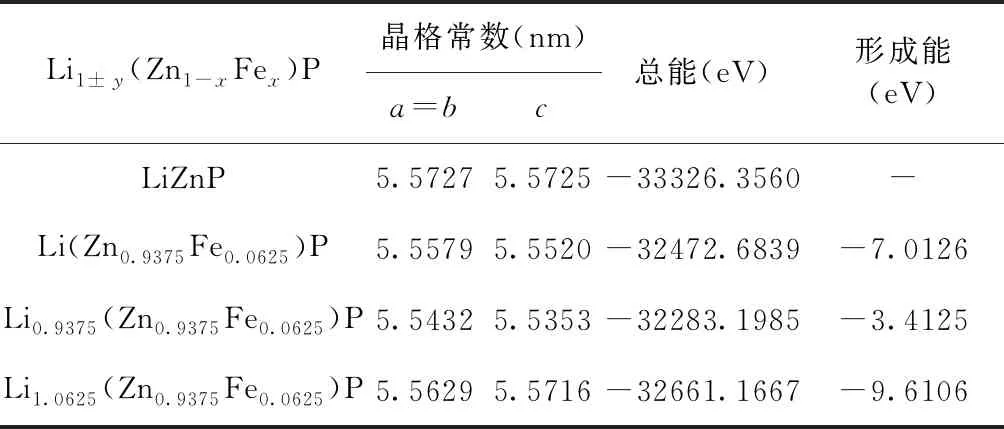
其中E[Li1±y(Zn1-xFex)P]和E[LiZnP]分别为掺杂和不掺杂体系的总能.n为改变的原子个数，μ为化学势，它们分别为各元素孤立的单个原子的能量.表1为Li1±y(Zn1-xFex)P体系的晶格常数、总能和形成能，发现掺杂体系的稳定性均有所提高，且在Li填隙时形成能最低，结构最稳定.

3 结果与讨论

3.1 纯LiZnP的电子结构

图2为纯LiZnP的能带结构和态密度图.由图2 (a)可知，本征LiZnP的导带底和价带顶都位于布里渊区G点处，表明LiZnP为直接带隙半导体，带隙值为1.031 eV，和实验值Eg=2.040 eV[16]

表1 Li1±y(Zn1-xFex)P的晶格常数、总能和形成能

Table 1 The lattice constants, total energies and formation energies of Li1±y(Zn1-xFex)P

Li1±y(Zn1-xFex)P晶格常数(nm)a=bc总能(eV)形成能(eV)LiZnP5.57275.5725-33326.3560-Li(Zn0.9375Fe0.0625)P5.55795.5520-32472.6839-7.0126Li0.9375(Zn0.9375Fe0.0625)P5.54325.5353-32283.1985-3.4125Li1.0625(Zn0.9375Fe0.0625)P5.56295.5716-32661.1667-9.6106

相比仍偏低.这是因为CASTEP计算能带，采用的密度泛函理论为基态理论，它在处理激发态问题时会导致计算结果与实验结果有较大的偏差，尤其是会低估半导体和绝缘体的带隙，但这并不影响对Li1±y(Zn1-xFex)P (x=0, 0.0625;y=0, 0.0625)体系性质的理论分析[23].由图2(b)，(c)和(d)的分波态密度图可知，体系的价带范围为-6.00 eV～0.00 eV，下价带主要由P3p、Zn4s态电子以及少量的P3s态电子组成，上价带主要由Li2s、P3p以及少量的Zn3d态电子组成.导带主要由Li2s，Zn4s，少量的P3s，P3p态电子构成.由图2(e)总的态密度可以看出体系自旋向上和自旋向下的能带结构对称，体系无净磁矩.

3.2 Li1±y(Zn1-xFex)P的电子结构

图2 LiZnP (a)能带结构图,(b)分波态密度图Li,(c)Zn,(d)P和(e)总态密度图Fig.2 The band structure (a), partial densities of states Li (b), Zn (c),P(d), and total density of states (e) of LiZnP supercell

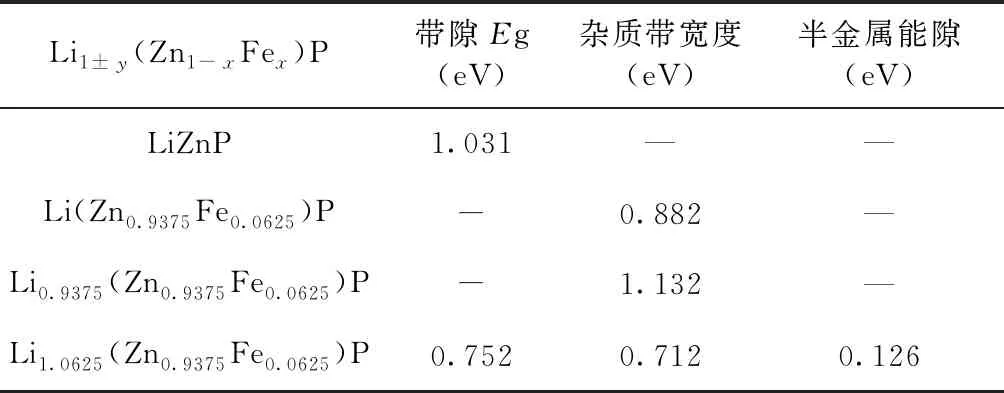
图3为掺杂体系的自旋极化能带图.由图3(a)和(b)可知，Fe掺杂后，最显著的变化是在费米能级(EF)附近出现与Fe有关的自旋极化杂质带，位于价带顶上方Ev+0.343 eV处，杂质带宽度为0.882 eV.其中自旋向上和自旋向下中的杂质带各5条，自旋向上的结构中3条杂质带位于EF上方，2条杂质带贯穿于EF中，表现为金属性；自旋向下的结构中，3条杂质带跨过EF，剩下的2条杂质带并入价带中，也表现为金属性，从而使体系整体上表现出金属性.与纯LiZnP相比，Fe的掺入显著提高了材料的导电性.图3(c)和(d)为Li空位时的自旋极化能带图，其能带结构与Fe单掺时相似，仍表现为金属性，但此时EF向导带移动，导电性较Fe单掺时减弱，杂质带宽度最大，为1.132 eV.图3(e)和(f)为Li填隙时的自旋极化能带图，Li填隙时杂质带宽度为0.712 eV，位于价带顶上方Ev+0.512 eV处，即在EF附近引入了空穴载流子.与Fe单掺和Li空位截然不同的是，自旋向上的能带结构中，杂质带未跨过EF，表现出半导体性质，带隙值为0.752 eV，而自旋向下EF贯穿在杂质带中，表现为金属性，从而使体系整体上表现出半金属性.半金属能隙为0.126 eV，明显表现为自旋注入，即杂质带中通过有效质量传输产生100%的自旋极化载流子注入.

表2 Li1±y(Zn1-xFex)P 的带隙、杂质带宽度和半金属能隙

Table 2 The band gaps, impurity energy bands and half-metallic energy gaps of Li1±y(Zn1-xFex)P

Li1±y(Zn1-xFex)P带隙Eg(eV)杂质带宽度(eV)半金属能隙(eV)LiZnP1.031——Li(Zn0.9375Fe0.0625)P-0.882—Li0.9375(Zn0.9375Fe0.0625)P-1.132—Li1.0625(Zn0.9375Fe0.0625)P0.7520.7120.126

图4为掺杂体系的分波态密度图和总态密度图.由图4(a)可以看出，Fe掺入后，对比纯LiZnP的态密度可知，自旋在费米能级处产生明显的劈裂，这主要是由Fe元素引起的.其中，费米能级附近出现新的峰Fe3d，而Zn3d对应的峰消失，P3p态电子态密度由原来较为尖锐的3个峰，变成相对较弥散的2个峰.这时跨过费米能级的子带，主要是自旋向下的P3p和Fe3d及少量的Li2s，Zn4s态电子构成，它们的轨道电子在费米能级附近出现重叠，表明体系产生了sp-d杂化作用.Fe的3d态电子在自旋向上时几乎完全被电子占据，自旋向下部分填充，劈裂为三重兼并的t2g能级和二重兼并的eg能级，对费米能级以下的占据态进行积分计算，结果如表3所示，可知其磁矩主要来源于Fe原子的2.83μB.Li原子、Zn原子、P原子贡献磁矩分别为0.08μB，0.21μB，0.61μB.故体系净磁矩为3.73μB，此时体系的净磁矩最大.

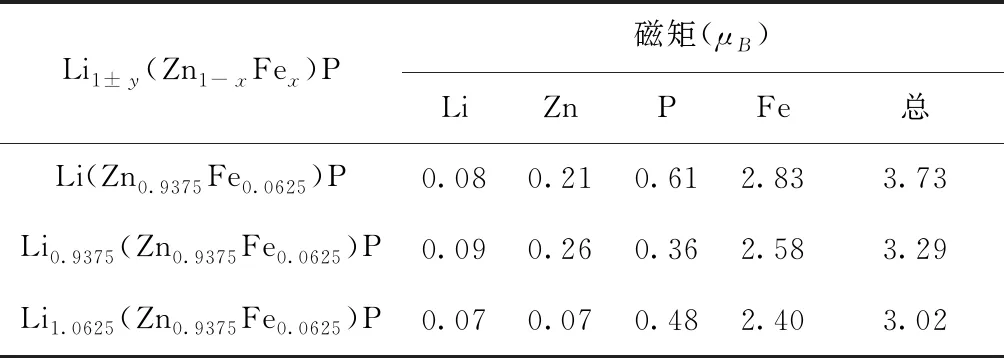
表3 Li1±y(Zn1-xFex)P体系的磁矩

图4(b)为Li空位的分波态密度图.由图可知，Li空位时，费米能级附近跨过费米能级的子带新增了态密度峰Zn3d，且P3p态密度峰在费米面处的值增大.但Fe3d电子态密度分裂出的eg能级向高能方向移动，t2g能级向低能方向移动，致使t2g能级处于部分填满，从而使得体系的sp-d杂化作用减弱，净磁矩减小为3.29μB.

图4(c)为Li填隙的分波态密度图.Li填隙时，Li2s，Zn4s的态密度与Li空位相比有所减小，P3p态密度峰略微增大.Fe3d电子态的t2g能级继续往费米能级上方推动，使得t2g能级处于半填满状态，eg能级移入价带，表明Li填隙使体系sp-d杂化作用进一步减弱.故Li填隙时，体系的净磁矩最小，为3.02μB.图4(d)为Li1±y(Zn1-xFex)P体系的总态密度图，与纯LiZnP相比，三种掺杂体系均发生了自旋劈裂，有净磁矩产生.根据Zener[24]理论，体系的居里温度TC与Fe3d态电子在费米能级处的态密度n3d(EF)和杂质带宽度W成正比：

图3 Li1±y(Zn1-xFex)P的能带图.(a)(b)Li(Zn0.9375Fe0.0625)P; (c)(d)Li0.9375(Zn0.9375Fe0.0625)P; (e)(f) Li1.0625(Zn0.9375Fe0.0625)P.Fig.3 The band structures of Li1±y(Zn1-xFex)P.(a)(b)Li(Zn0.9375Fe0.0625)P;(c)(d)Li(Zn0.9375Fe0.0625)P; (e)(f)Li1.0625(Zn0.9375Fe0.0625)P.

图4 Li1±y(Zn1-xFex)P的分波态密度.(a)Li(Zn0.9375Fe0.0625)P; (b)Li0.9375(Zn0.9375Fe0.0625)P; (c) Li1.0625(Zn0.9375Fe0.0625)P; (d)总的态密度图Fig.4 The partial densities of states.(a)Li(Zn0.9375Fe0.0625)P; (b)Li0.9375(Zn0.9375Fe0.0625)P; (c) Li1.0625(Zn0.9375Fe0.0625)P; (d)total density of states.

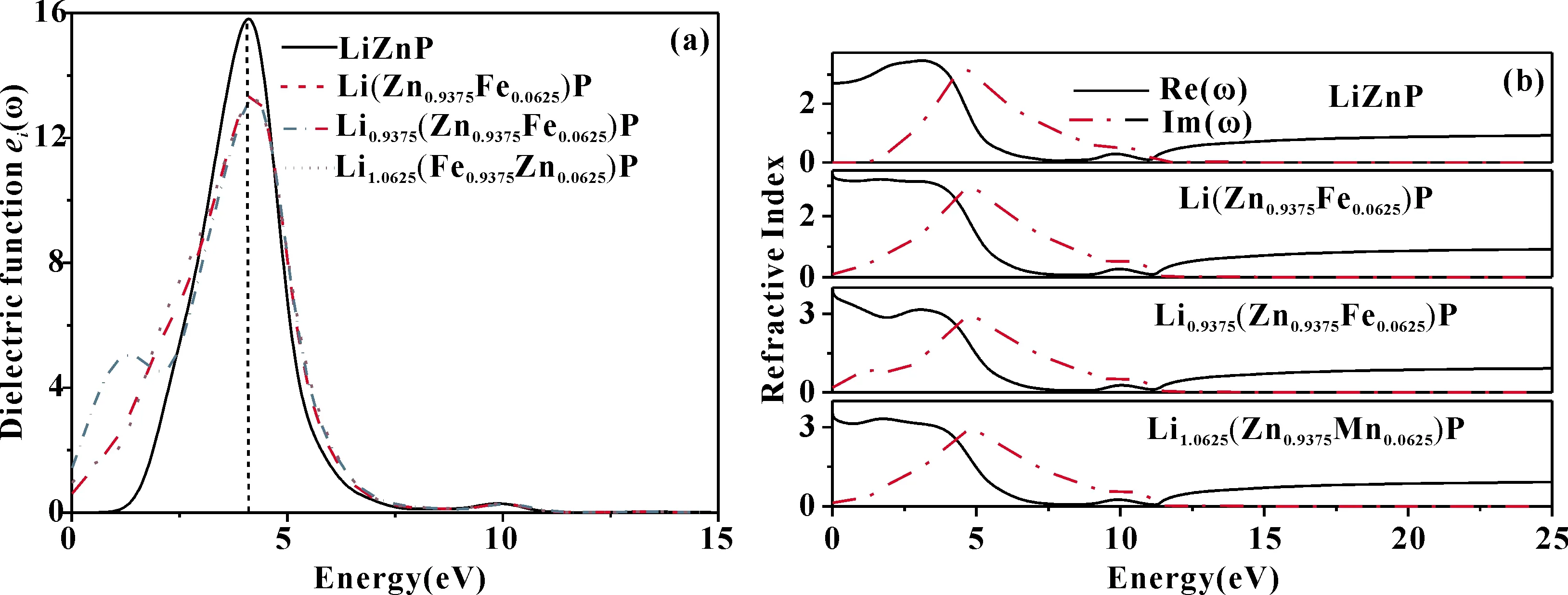
图5 Li1±y(Zn1-xFex)P的介电函数虚部(a)和复折射率函数(b)Fig.5 The imaginary part of dielectric function (a) and the complex refractive index function (b) of Li1±y(Zn1-xFex)P

TC∝W·n3d(EF),

(2)

Li空位时，Fe3d电子在费米能级处的态密度增大，由表2可知，此时杂质带宽度也最大，表明Li空位可以提高掺杂体系的居里温度，这与Sato等人[10]理论计算的VLi可以提高体系的TC相符.

3.3 Li1±y(Zn1-xFex)P的光学性质

对材料光学性质的研究，是分析半导体物理性质最基本的手段.本文对掺杂前后体系的介电函数虚部、复折射率函数、光吸收光谱和能量损失进行了计算和分析.在线性响应范围内，半导体的宏观光学特性可以采用复介电函数来描述：

ε(ω)=εr(ω)+iεi(ω)

(3)

其中，εr(ω)=n2(ω)+k2(ω)，εi(ω)=2n(ω)k(ω).介电函数虚部和实部之间的关系可通过克喇末-克朗尼格(Krames-Kronig，K-K)关系得到[25-27].

图5为纯LiZnP和掺杂体系的介电函数虚部和复折射率函数.掺杂前后均未改变材料半导体的性质，能级间的跃迁产生了其光谱，可由能带结构和态密度来解释其介电峰的来源[25,26].从图5(a)中可以看出纯LiZnP在能量为4.1 eV出现介电峰，对比态密度图2(b)，(c)和(d)可知，这对应着体系的直接跃迁阀，主要是价带的P3p态电子向导带Li2s、Zn4s和P3s跃迁的结果.它与体系带隙存在偏差的原因是电子跃迁吸收能量应考虑跃迁过程中的弛豫效应，而不是简单的两个能级差[28,29].Fe掺入后，与直接跃迁对应的介电峰稍向高能区移动，且峰值减弱，这是由于Fe掺杂后在带隙中引入杂质带，使得光学带隙增大的缘故.Li空位时，一个明显现象是在低能区出现新的介电峰，且之前的介电峰较纯LiZnP减弱，这主要是由于价带电子向杂质带跃迁产生介电峰，同时引入杂质带后能级间的相对跃迁几率变小.Li填隙时，杂质带并入价带，所以新增介电峰消失.

由图(b)的复折射率函数可知，纯LiZnP在E<1.52 eV的低能区和E>11.22 eV的高能区，虚部均为0，实部趋于常数.表明纯LiZnP体系对电磁波吸收限制在一定频率范围内.Fe掺杂后，峰值略向高能区方向移动，这是由于Fe的掺入引起的sp-d轨道杂化使能带偏移而导致的.Li空位时，在低能区出现新的吸收峰，主要是由于Li的化学计量数改变后，电磁波通过的介质密度不同，造成折射率函数发生变化，增大了体系对低频电磁波的吸收.Li填隙时，新增介电峰消失，与体系能带结构的变化相对应.

图6 Li1±y(Zn1-xFex)P的光吸收谱(a)和能量损失谱(b)Fig.6 Optical absorption spectra (a) and energy loss spectra (b) of Li1±y(Zn1-xFex)P

图6(a)和(b)是纯LiZnP和掺杂体系的光吸收谱和能量损失谱图.由图(a)可以看出， LiZnP的吸收边能量分别是1.18 eV和11.79 eV，吸收主峰在4.9 eV左右，这与体系的直接跃迁阀对应.掺入Mn之后，掺杂体系的吸收峰均向高能区移动，而且吸收范围也有所增大，增大了体系对高频电磁波的吸收，而Li空位和Li过量又在这个基础上继续向高能区方向移动，这与复折射率函数虚部的特征峰在高能区的变化对应.由图(b)的能量损失谱可以看出，纯LiZnP的能量损失谱在11 eV左右，掺杂体系的峰均向高能方向移动，呈现明显的蓝移特征.Fe单掺和Li空位时，能量损失峰均有所减少，分别为纯LiZnP的95%和66%.Li填隙时，能量损失峰的峰值较纯LiZnP和其他掺杂体系明显增大，说明Li填隙时有更强的等离子体共振频率[30].

4 结 论

采用基于密度泛函理论的第一性原理计算法研究了新型稀磁半导体Li1±y(Zn1-xFex)P (x=0, 0.0625;y=0, 0.0625)的电子结构、磁性及光学性质.结果表明，Fe的掺入使得Fe3d态与Li2s，Zn4s以及P3p态发生sp-d轨道杂化，使能带劈裂，在费米能级产生杂化峰，净磁矩为3.73μB，体系表现为金属性，导电性增强.Li空位时，费米能级向价带移动，Fe3d态密度峰在费米面处的峰值减小，体系轨道杂化减弱，净磁矩减小，但体系杂质带宽度最大，居里温度最高.而Li填隙时，体系变为半金属性，半金属能隙为0.126 eV，形成能降低，结构最稳定.表明Li1±y(Zn1-xFex)P体系可以通过Fe的掺入和Li含量的调控，实现自旋与电荷注入机制的分离.通过比较光学性质发现，Fe掺入后，在介电函数虚部、复折射率函数、吸收函数、损失函数的低能区均有明显变化，且Li空位时，介电函数虚部和复折射率函数在低能区出现新峰，吸收边向低能方向延展，增大了对低频电磁波的吸收.掺杂体系的能量损失峰均向高能方向偏移, 呈现出明显的蓝移特征，且Li填隙时，损失峰的峰值明显增大，表明Li填隙具有更强的等离子体共振频率，而Li空位时能量损失最小.