复杂流道结构料仓的下料流率预测

孙栋，陆海峰，曹嘉琨，吴雨婷，郭晓镭，龚欣

（华东理工大学上海煤气化工程技术研究中心，上海200237）

引 言

作为储运粉体的重要单元操作设备，料仓简单的结构获得了工业界的青睐[1-2]，在其中复杂的颗粒流动现象也受到科学研究者的广泛关注[3-5]。近50年间，围绕颗粒静态堆积、动态流动和塑形流变等行为的研究大量开展[6]，但由于受到颗粒间非线性和不可逆的受力-变形行为[7]，力链结构强度迥异、互相交接[8]等复杂因素的影响，颗粒的流动机理仍没有得到充分掌握[9]。受限于复杂的颗粒特性、迥异的操作条件和变化的结构参数，颗粒在料仓中展现出不同的流动行为，例如质量流、中心流，在某些极端的情况下，会出现结拱、鼠洞、死区等异常现象[10-11]。

颗粒流动顺畅、连续以及料仓结构稳定、耐久[12]是评价下料过程的重要指标。通气[2,13]、振动[14-15]和改流体[16-17]是调节料仓中颗粒流动形态，改善不正常操作的常用手段。Lu 等[18]在中试装置中研究了通气对粉煤下料的影响，依据下料过程的团聚模型成功预测了下料流率。Matchett[19]建立了拱稳定模型，考虑了主动态和被动态不同的作用规律，指导了振动料仓的下料过程。作为一种简便的料仓流动调节手段，改流体对流型的影响得到了广泛关注[20-21]，但其对流率的促进作用往往被忽视，缺乏改流体料仓下料流率的预测方法。

在平底圆柱料仓中，Beverloo 方程[22]被广泛用来预测下料流率。为了提高预测精度，扩展适用范围，Beverloo 方程被反复修正。Tierrie 等[23]采用摄像捕捉的方法，对颗粒的形状进行了描述，给出了修正Beverloo 方程中形状参数的指导方法。Lu 等[4]从颗粒间作用力的角度出发，考察了表面粗糙度对下料流率的影响，基于Bond 数划分了下料的流型，预测了下料流率。在锥形料仓中，颗粒沿壁面滑动甚至滚落，必将对下料流率产生影响，Khashayar 等[24]认为锥形料仓不能视为平底料仓的特例。在半锥角α 的料仓中，Rose 等[25]引入校正因子f = (tanα tanφd)-0.35来反映料仓半锥角的作用效果。基于力平衡的原理，Carleton[26]得到了锥形料仓出口处颗粒的平均速度，对下料流率进行了预测。作为调节流动的常用手段，掌握并预测改流体对粉体下料流率的影响规律十分必要。然而目前对料仓改流体的研究大多是关于调节流型的报道，缺乏对粉体下料流率变化的定量分析，更没有成熟的理论模型能够预测加装改流体后的复杂流道结构料仓的粉体下料流率。

本文借助实验室有机玻璃料仓，考察了传统料仓(无改流体)和加装改流体料仓(封闭改流体和开放改流体)的粉体下料特性，研究了不同结构的复杂流道对玻璃微珠、煤粉和聚氯乙烯三种粉体下料流率的作用规律；然后基于不同流道下粉体特有的流动现象，并综合考虑物料性质以及料仓结构的影响，在对最小能量理论方程进行修正的基础上，建立包含粉体物性、下料流型和流道结构影响的粉体下料流率预测模型。本研究对下料过程的强化与料仓结构优化设计具有一定的指导意义。

1 实验物料及方法

1.1 实验物料

本文选取不同粒径的玻璃微珠(glass bead-a、glass bead-b、glass bead-c)、褐煤(lignite)和聚氯乙烯颗粒(pvc)作为实验物料，通过气动筛分后(Retsch AS200 Jet Air)，得到Span 指数较小的窄粒径分布的样品，规避宽的、不规则的粒度分布对下料流率的影响。借助马尔文激光粒度仪(Malvern 2000)对样品的粒径大小与粒度分布进行测试，结果如图1 所示，其中glass bead-c、lignite 和pvc 的粒径分布近似相同。表1给出了颗粒的表面积平均粒径(d32)、体积平均粒径(d43)和分布宽度Span指数。

图1 粒径累积分布Fig.1 Accumulative particle size distribution

表1 物性数据Table 1 Physical properties of experimental materials

借助FT4 粉体流变仪(Freeman technology)和PT-X 型粉体流动性-喷流性测量仪(Hosokawa Micron Corporation)对实验物料的流动性质和堆积性质进行了表征，得到了如表1 所示物料的堆积密度(ρb)、休止角(AOR)和内摩擦角(AIF)等流动性参数。以休止角作为表征物料流动性的参数，可知，glass bead-b 的流动性最好，属于自由流动粉体；lignite 的流动性最差，属于黏附性粉体。实验前在105℃下对物料进行烘干处理，烘干后使用红外水分测试仪(Sartorius MA150)测 量glass bead-a、glass bead-b、glass bead-c、lignite 的水分含量分别为0.02%、0.08%、0.08%和0.21%，可以忽略湿含量对颗粒流动的影响。

1.2 实验方法

下料实验在有机玻璃料仓中进行，实验装置如图2 所示，打开滑动阀后，料仓内的物料从出口流出，沿斜槽滑落到接料盘中。整个下料过程的质量变化由连接到计算机上的电子秤实时采集，精度为0.1 g，采样频率为8 Hz。从离散点绘制的下料曲线中可以得到物料的质量流率。

图2 下料实验装置Fig.2 Diagram of discharge device

为了考察不同流道结构料仓内的粉体流动规律，在30°半锥角的有机玻璃料仓中内置了半锥角为15°的改流体，并且改流体分为封闭式和开放式两种。图3 给出了料仓、改流体的结构参数及其装配方式。改流体位于料仓出口上端30 mm 处，如图中虚线所示，两者在料仓出口处具有相同的口径。

图3 设备尺寸参数Fig.3 Device parameters

根据料仓和改流体的装配方式，本文研究了图4 所示的三种流动通道下粉体的下料规律，分别为无改流体料仓(No-In)、封闭式改流体料仓(Con-In)和开放式改流体料仓(Ucon-In)。无改流体料仓是常用的锥形料仓，整个锥体作为粉体的流动通道；所谓封闭式改流体料仓，意味着粉体无法从改流体内部流过，只能在改流体和料仓构成的夹层间流动；所谓开放式改流体料仓，表明粉体可以同时在改流体内部、改流体和料仓夹层间流动。

图4 下料操作模式(阴影部分为非流动区)Fig.4 Discharge operation modes(hatched domain is notavailable for flow)

2 结果与讨论

2.1 复杂流道下料

图5所示为粉体通过不同流道结构的流动示意图。在No-In 的作用下，整个料仓作为流动通道，物料以中心流动快、边壁流动慢的方式从料仓出口卸出；引入改流体后，Con-In 作用下的物料流动，在径向方向上速度均匀性得到增强，在图5 中表现为代表大速度梯度的深色阴影区面积减小；在Ucon-In的作用下，改流体内部的物料先于夹层间的物料流出，存在流动竞争的特殊流动现象。分析摄像拍摄的下料过程可知，两个流动通道内的过程独立进行，不存在物料的相互混合。

Janssen 效应的存在解释了不随时间变化的下料流率。本实验体系下，在No-In 和Con-In 的作用下，料仓内物料的剩余质量随时间均匀减少，不随时间改变的下料流率，可通过线性拟合下料曲线获得。在Ucon-In 的作用下，下料曲线存在转折点，同样采用线性拟合的方式，平均化处理两段过程，得到下料流率。

表2给出了不同流道结构下各种物料的下料流率。在所有的流道结构下，三种glass bead 的下料流率接近，远大于lignite和pvc的下料流率。值得注意的是，尽管glass bead-c、lignite 和pvc 粒径分布相当，但三者的下料流率差异较大。glass bead-c 作为理想介质，大的真密度、小的黏附性，重力驱动下的流动效果最好。对于lignite，一方面表面粗糙，孔隙结构发达，颗粒间作用力较为复杂，黏聚性较强；另一方面，lignite 的大颗粒含量更多，大小颗粒镶嵌流动，不利于顺畅下料。对于pvc，真密度小，下料过程重力驱动的作用不显著；同时，易摩擦带电的性质增加了颗粒间的静电相互作用，不利于颗粒的流动。

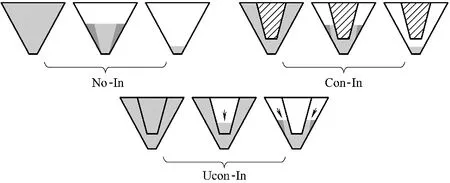
图5 下料流动顺序Fig.5 Diagram of sequential flow order during discharge

表2 下料流率实验值Table 2 Experimental value of discharge rate

引入改流体调整流道结构后，在Con-In 和Ucon-In 的作用下，物料的下料流率得到了增大。Con-In 作用下，物料的下料流率最大，促进流动的效果最为明显。下料流率的提升程度如图6 所示，性质不同的物料，下料流率的提升程度也不尽相同，但Con-In 和Ucon-In 具有相同的影响趋势。在Con-In 的作用下，glass bead-b 下料流率的提升幅度为最小的16%，lignite 的提升幅度为最大的58%。结合表1 可知，对休止角大、流动性差的物料，流道结构改变对下料流率的提升幅度更加明显。

2.2 复杂流道下料流率预测

图6 流道结构对下料流率提升幅度的影响Fig.6 Relationship between increase of discharge rate and flow channel structure

尽管研究者们对粉体下料流率的建模研究已经开展了大量工作，但针对改流体料仓，目前还没有这方面的相关报道。本文从传统料仓的下料模型出发，综合考虑粉体物性、下料流型和流道结构的影响，最终建立具有普适性的复杂流道结构的料仓下料流量预测模型。

2.2.1 无改流体料仓（No-In）下料模型修正 基于“free-fall arch”和“minimum energy theory”的原理，Brown 等[27]在图7 所示的坐标系统下，提出以下假设：①固体颗粒连续性方程中“free-fall arch”附近的物质膨胀可以忽略；②在“free-fall arch”下方固体颗粒应力σ的变化相对于其他部分对总能量的影响是可以忽略不计的；③假设颗粒径向流动；④“freefall arch”理想表面位置是假定在料仓出料口边界径向坐标r=r0处。

图7 坐标轴系统结构Fig.7 Schematic diagram of coordinate system

基于这些假设，得到了最小能量理论方程式(1)，可用于预测理想物料以理想流动状态流出料仓时的下料流率。

式中，Ws是下料流率，kg·s-1；α 是料仓半锥角，（°）；ρb是物料的堆积密度，kg·m-3；g 是重力加速度，m·s-2；Do和dp分别是料仓出口直径和颗粒直径，m；k是无量纲的Beverloo常数。

然而，一方面，受到颗粒形状、粒径分布和表面材质等因素的影响，粉体的性质会偏离理想物料。另一方面，细颗粒在料仓中心附近膨胀快，边壁附近膨胀慢，引发了料仓内的速度梯度。所以，“freefall arch”附近的物质膨胀不再可以忽略，物料不再服从理想流动。因此，如表3所示，式(1)对实际过程下料流率的预测产生了偏差，预测值偏大，对lignite的预测偏差达到了39.7%，不能正确地反映实验规律。下面依据实验中的流动现象修正理论模型，将其拓展至实际下料过程。

Freyssingeas 等[6]描述了黏性颗粒下料过程中自由表面的波动情况，图8 所示为时间叠合下的物料主要流动区的变化。下料过程中，物料并非以理想质量流的方式流向出口，而是分层分级向出口流去。

图8 下料过程物料自由表面的变化[6]Fig.8 Free surface during powder discharge process[6]

如图9所示，本实验体系下，出现了同样的流动现象。glass bead-c 的自由表面存在凹陷，料仓中心处的流动速度快于壁面附近，物料并非以理想质量流的方式卸出。因此，将料仓中的流动区域分为快速流动区(fast flow zone)和剪切摩擦区(shear flow zone)。所谓的快速流动区分布在料仓中心处，颗粒运动速度快且分布均匀，粉体以理想质量流的方式流向出口；所谓的剪切摩擦区则分布在料仓边壁附近，存在速度梯度。

图9 玻璃微珠的下料过程Fig.9 Diagram of discharge of glass bead

摩擦特性的存在是实际物料偏离理想物料的的主要原因，物料性质的差异造成了实际流动与理想流动的不一致。假定剪切摩擦区对下料流率没有贡献，借助实验值与式(1)所得理论值的比值来反映料仓中剪切摩擦区的面积大小，lignite 剪切摩擦区的面积高达40%。式(1)对下料流率的预测偏大，可归结为剪切摩擦区的影响。

以此为依据，对下料流率方程进行修正。基于Rose 等[25]死区与水平方向夹角Φd的理念，以反映颗粒间的摩擦特性和抗剪特性的内摩擦角φ近似作为快速流动区与剪切摩擦区的划分边界，对式(1)进行修正，引入如式(2)所示的校正因子F

表3 No-In下料模式下实验值与预测值的偏差Table 3 Deviation between experimental value and theoretical value under No-In mode

对于实际物料，受到剪切流动的影响，下料流率低于理想流动，所以校正因子F＜1。随着内摩擦角的增大，物料受剪切区的影响增大，下料流率减小，校正因子F也相应减小。

将校正因子F 代入式(1)中，便得到下料流率预测公式

式中，Ws'是下料流率，kg·s-1;φ是物料的内摩擦角，(°); α 是料仓半锥角，(°); ρb是物料的堆积密度，kg·m-3；g 是重力加速度，m·s-2；Do和dp分别是料仓出口直径和颗粒直径，m; k 是无量纲的Beverloo常数。

表3 给出了所有物料下料流率的实验值，式(1)计算所得的理论值，式(3)计算所得的修正值以及相对应的偏差。考虑了剪切摩擦区影响的式(3)提高了下料流率的预测精度。

如图10所示，使用式(3)对文献[28-30]中的下料流率值进行预测。文献涉及煤粉、玻璃微珠等多种物料，10°、20°等不同的锥角以及22.7、32.8 mm 不同的开口直径。下料流率覆盖范围从100 g·s-1左右到800 g·s-1左右。修正后计算公式的精度提高，并将理想的料仓下料模型拓展至实际下料过程。

2.2.2 封闭式改流体料仓（Con-In）下料模型修正

在料仓中引入改流体，形成复杂的流道结构，强化了流动过程，提升了下料流率，具有潜在的应用价值。准确预测下料流率可以对强化下料过程与优化料仓结构做出指导。

如图11 所示，流道结构从No-In 变为Con-In后，流动区域的发展衍变规律发生了改变。对于快速流动区：①由料仓中心向边壁位置转移，颗粒的径向速度获得了增大；②不对称壁面的剪切作用更加充分。这使得Con-In 流道内的物料具有了更大的能量密度，快速流动区得到更加充分的发展，有利于下料流率的提升。对于剪切摩擦区：狭小的体积使得剪切摩擦区的发展空间受到限制，无法充分衍变，相较之下，快速流动区所占比重增大，物料的下料流率获得提升。

图10 实验值与预测值的比较Fig.10 Comparison of experiment and model values of discharge rate

图11 流动区域转变示意图Fig.11 Schematic diagram of flow zones transition

确定料仓中剪切摩擦区的影响以及流道结构的特征参数对提高预测公式的准确性具有较大的意义。

由上文可知，式(2)中校正因子F的引入，可以较好地反映剪切摩擦区的影响。所以，预测Con-In 流道结构下的下料流率时，仍然借用F 因子反映剪切摩擦区的影响。

流道结构改变后，锥角是对结构特征的直接反映，特征锥角的确定将尤为关键。图12 分析了Con-In 作用下粉体的受力情况，微元粉体受到来自不对称壁面的支撑力和摩擦力以及重力的作用，水平方向的力平衡关系如式(4)所示

图12 Con-In作用下粉体受力示意图Fig.12 Schematic diagram of force analysis of powders under Con-In

式中，Fi、Fh为壁面对粉体的摩擦力，N；Ni、Nh为壁面对粉体的支撑力，N；αi为改流体半锥角，αh为料仓半锥角，(°)。

竖直方向的力平衡关系如式(5)所示

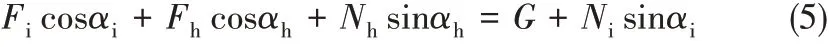
根据Coulomb-Mohr 定律[25]，不考虑物料的内聚力，则

式中，μ是物料的摩擦系数。

将式(6)代入式(4)、式(5)，联立求解，则

其中

由此可知，料仓半锥角(αh)与改流体半锥角(αi)的差值决定了粉体在复杂流道中受到的支撑力与摩擦力的大小，是影响粉体运动的关键参数。借用此差值对原有模型中的锥角项进行修正。

综上，考虑剪切摩擦区以及料仓结构的影响，可借助式(10)对Con-In 流道结构的下料流率进行预测。

式中，特征锥角α'修正为料仓半锥角(αh)与改流体半锥角(αi)之差。

表4给出了不同物料下料流率的实验值以及式(10)计算所得的修正值。结果表明，考虑了剪切摩擦区以及复杂流道结构影响后的式(10)可以较好地预测下料流率。

2.2.3 开放式改流体料仓（Ucon-In）下料模型修正

相比于No-In，Ucon-In 可以提高物料的下料流率，Con-In 的作用效果更加明显。对Ucon-In 而言，物料流动通道的增加，并没有带来下料流率的增长。由图5 可知，在Ucon-In 的作用下，存在竞争流动导致的分阶段下料现象。图13给出了Ucon-In作用下glass bead-c 的瞬时下料流率，存在流率变化的转折点，拐点前后下料流率平均值不同，第二阶段的下料流率值与Con-In 作用下的下料流率数值吻合。低速下料的第一阶段的存在，使得Ucon-In 流道下的下料流率小于Con-In 作用下的下料流率。因此，进行流率预测时，需要充分考虑这一特殊的流动现象。

表4 Con-In下料模式下实验值与预测值的偏差Table 4 Deviation between experimental value and theoretical value under Con-In mode

图13 Ucon-In作用下的瞬时流率Fig.13 Diagram of variation of sample instantaneous discharge rate with time in silo with unconfined insert

从改流体内部流出的物料受到出口直径变化的影响，下料流率小于从夹层间流出的物料。理想情况下，物料在料仓中的堆积密度分布均匀，计算得出质量占比为m 的物料受到出口直径变化的影响而导致流率减小。因此，可借助式(11)对Ucon-In流道结构的下料流率进行预测。

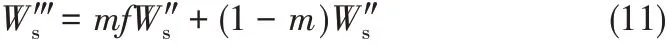
如图14 所示，对不同物料，两个阶段下料流率的比值近似满足线性关系，因此式(11)中f 因子可视为一个不受物性影响，与料仓结构有关的参数。

图14 两个阶段下料流率的关系Fig.14 Relationship of discharge rate between two stages

由式(1)可知，下料流率与出口直径呈2.5 次方，所以考虑了出口直径影响的校正因子f 以式(12)的形式给出。

因此，便可获得如式(13)所示的，Ucon-In 流道结构作用下的下料流率预测公式。

式中，W‴s是下料流率，kg·s-1；m 是改流体内物料的质量占比；Di、Dh分别为改流体和有机玻璃料仓的出口直径，m。

2.2.4 下料流率综合预测 综合上述三种不同料仓结构下的下料流动现象和流率预测，对于传统料仓和复杂流道结构料仓中的颗粒流动，可以使用式(14)进行流率预测。

图15 给出了复杂流动通道作用下实验值和预测值的比较结果，预测公式符合实验规律，预测误差在±10%以内。

3 结 论

本文研究了不同粉体在No-In、Con-In和Ucon-In 流道结构作用下的流动特性和流率规律，并分别建立模型对其下料流率进行了预测，得到的主要结论如下。

图15 实验值与预测值的比较Fig.15 Comparison of experiment and model values of discharge rate

(1)改流体具有显著提升粉体下料流率的作用，且相比于Ucon-In，Con-In 促进流动的效果更佳。Ucon-In 流道结构料仓由于存在流动竞争现象，尽管实际流动通道较大，但粉体的下料流率低于Con-In 流道结构料仓。对于黏附性煤粉，Con-In 对下料流率提升幅度可高达58%，表明加装封闭式改流体是改善黏附性粉体下料的有效手段之一。

(2)物料的摩擦性质导致了料仓实际下料过程偏离理想流动，使得用于预测粉体下料流率的传统模型出现偏差。本文定量计算的剪切摩擦区面积解释了偏差存在的原因，并进一步提出流率校正因子，综合考虑物料性质和区域流动的作用，对最小能量理论方程进行了修正，将理想的料仓下料模型拓展至实际下料过程。

(3)针对加装改流体后的复杂流道结构料仓，分别建模分析了Con-In和Ucon-In流道结构下粉体的下料流率。对于Con-In，受到不对称壁面的剪切作用，料仓半锥角无法反映仓壁的影响，引入了特征参数α'对下料模型进行修正；对于Ucon-In，基于粉体流动竞争机制和内外流道内的流率关系对下料模型进行修正。在上述基础上，建立了综合考虑了粉体物性、下料流型和流道结构影响的下料流率预测模型，预测偏差＜10%。