基于PR立方型状态方程普遍化温度函数的研究与评价

赵文英，李文文，孙晓岩，曹晓荣，项曙光

（1 齐鲁师范学院化学与化工学院，山东济南250200； 2 青岛科技大学过程系统工程研究所，山东青岛266042）

引 言

立方型状态方程是中等至高压体系纯组分蒸汽压和流体混合物汽液平衡及焓、熵、热容等热力学性质预测的重要方法。van der Waals[1]首次提出适用于真实气体的立方型状态方程，Redlich 和Kwong[2]改进VDW EoS 引力项的形式并将引力项系数a 关联为Tr0.5的温度函数得到RK EoS，但对纯物质蒸汽压的预测精度不高。Soave[3]发现烃类物质的α0.5与(1-Tr0.5)呈线性关系，并将系数m 普遍化为偏心因子的函数，得到著名的SRK EoS，提高了对非极性和弱极性物质蒸汽压的预测精度，但对液体体积的预测结果偏差较大。Peng 和Robinson[4]改进RK EoS 引力项的形式并重新关联Soave[3]温度函数的系数m，得到PR EoS，能够准确预测非极性和弱极性物质的蒸汽压，且提高了液体体积的预测精度。SRK 和PR EoS 对非极性和弱极性物质蒸汽压的预测结果均比较准确，但对极性物质蒸汽压预测结果的偏差较大。

引力项中温度函数的形式影响状态方程对蒸汽压的预测精度。Mathias 和Copeman[5]在Soave[3]的基础上增加(1-Tr0.5)的项数，提高了PR EoS 对极性物质蒸汽压的预测精度。Stryjek 和Vera[6]将Soave系数m 关联为Tr的函数，提高了低对比温度区域蒸汽压的预测精度。Twu等[7-8]、Gasem等[9]、Le Guennec等[10]、Mahmoodi 等[11]、Pina-Martinez 等[12]和Ghoderao等[13]不断研究改进温度函数的形式，以提高温度函数对蒸汽压的预测精度。Zhao等[14]对适用于立方型状态方程的多项式温度函数进行了概述。改进的温度函数能够预测纯物质的蒸汽压等热力学性质，但由于温度函数的参数与物质一一对应，受参数的限制，适用范围窄。Soave[3]最早提出普遍化温度函数，此 后Twu 等[15]、Coquelet 等[16]、汪 萍 等[17]、Li 和Yang[18]、Forero 等[19]、Le Guennec 等[10]、Mahmoodi 等[11]不断研究温度函数普遍化的方法，用于非极性、弱极性和极性物质蒸汽压的预测。

本文拟在PR EoS 的基础上，用70 种非极性、弱极性和极性物质对17 种普遍化温度函数预测蒸汽压的能力进行评价，总结普遍化温度函数的特点，确定较好的普遍化温度函数的形式和特点，为温度函数普遍化方法的改进提供借鉴。

1 普遍化温度函数模型

自Soave[3]提出普遍化温度函数以来，研究者不断改进温度函数的形式，得到上百种温度函数[14]，但普遍化的温度函数形式较少。通过整理，得到17种适用于PR EoS 的普遍化温度函数，其中5 种多项式温度函数，12 种指数温度函数。5 种多项式温度函数中Peng-Robinson(1976)[4]和Robinson-Peng(1978)[20]是应用较多的普遍化温度函数；后来，Coquelet等[16]、汪 萍 等[17]、Valiollahi 等[21]分 别 对Mathias-Copeman(1983)[5]、Stryjek-Vera(1986)[6]和Valiollahi 等(2016)[21]温度函数的参数普遍化。普遍化的指数温度函数种 类 较 多，Gasem (2001)[9]、Joshipura (2009)[22]、Li-Yang (2011)[18]、Haghtalab (2011)[23]、Saffari-Zahedi(2013)[24]、Hou (2015)[25]、PR-PM (2017)[11]和PR-PM2(2017)[11]是新提出且直接普遍化的温度函数，Le Guennec 等[10]、Forero 等[19]、Mahmoodi 等[11]则 分 别 对Twu (1988)[7]、Heyen (1980)[26]、Twu (1995)[15]和Coquelet (2004)[16]温度函数重新普遍化。普遍化的温度函数及参数关联式见表1。

表1 用于评价的普遍化温度函数Table 1 Generalized alpha functions for evaluation

续表

续表

2 评价方法

用11类共70种物质，在0.42～1.0对比温度范围内的4453 个实验饱和蒸汽压数据对17 种普遍化温度函数进行评价。各物质的实验蒸汽压数据参考文献见表2，临界性质和偏心因子等特性参数源自《Thermophysical Properties of Chemicals and Hydrocarbons》[27]。

将物质的特性参数带入普遍化的温度函数关联式，根据汽液相平衡时汽相逸度等于液相逸度的条件，计算该温度下的饱和蒸汽压。对蒸汽压的计算借助于Matlab 软件，用roots函数求解压缩因子(Z)的三次方程，fsolve 函数求解汽液相平衡时的蒸汽压。

饱和蒸汽压的相对偏差(RD)和平均相对偏差(ARD)计算表达式见式(1)、式(2)。

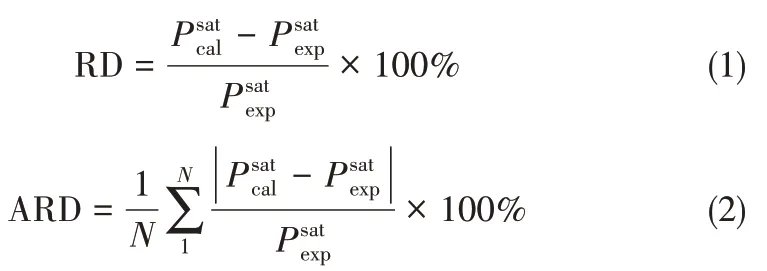
表2 11类物质基本信息Table 2 Basic information of 11 kinds of compounds

3 结果与讨论

3.1 整体分析预测结果

17 种普遍化温度函数对11 类物质的预测结果见图1。从图1 可以看出，Hou (2015)温度函数对各类物质的预测结果偏差最大，平均相对偏差为13.90%，其次为Saffari-Zahedi(2013)温度函数，平均相对偏差为6.56%,主要用于天然气体系的汽液平衡计算，Hou等[25]在Saffari-Zahedi(2013)的基础上重新关联温度函数的参数，用于富含CO2天然气体系的汽液平衡预测。Saffari-Zahedi (2013)对C8以下的烷烃和芳烃、气体、醚、酯等小分子物质的预测结果较准确，但对极性物质和分子量较大的非极性物质的预测结果偏差较大。单参数的Joshipura(2009)温度函数对蒸汽压预测结果的偏差也较大，平均相对偏差为6.18%，其中对正构醇、正构烷烃、气体和酸类物质预测结果的平均相对偏差超过9%。预测结果最准确的是Forero (2016)温度函数，对11 类物质蒸汽压预测结果的平均偏差为3.09%。 Peng-Robinson (1976)、 Robinson-Peng(1978)、Gasem (2001)、Li-Yang (2011)等13 种温度函数对蒸汽压预测结果的平均相对偏差接近，介于3.64%～4.50%。

3.2 正构烷烃的预测结果

17 种普遍化温度函数对C1～C20、C22和C24共22种正构烷烃蒸汽压的预测结果见图2。从图2 可以看出，Hou (2015)温度函数对烷烃蒸汽压的预测结果整体偏差，尤其对于C9以上烃类物质蒸汽压的偏差显著增大，平均相对偏差超过20%，对C18以上重烃类物质蒸汽压的预测结果的偏差超过45%，最高达77.9%。Saffari-Zahedi (2013)对烷烃蒸汽压的预测结果略优于Hou(2015)温度函数，自正壬烷开始，预测结果的偏差显著增大，大于5%。开发用于天然气露点计算的Valiollahi(2016)温度函数，对C18以上烷烃预测结果的最大偏差小于7.5%，但对C18以上重烃预测结果的偏差显著增大，高达29.4%；对22种烃类物质蒸汽压预测结果的平均相对偏差为6.28%，与Peng-Robinson (1976)温度函数的预测结果接近(6.27%)。Joshipura (2009)温度函数对22 种烃类物质蒸汽压预测结果的平均相对偏差为9.13%，高于Peng-Robinson (1976)温度函数的预测结果。剩余12 种温度函数对C8以下烃类物质蒸汽压预测结果的偏差接近，平均相对偏差均小于2.5%，但对C8以上烃类物质的预测结果产生差异。PR-PM (2017)、PR-PM2 (2017)、Twu-Mahmoodi(2017)、Le Guennec (2016)、Haghtalab (2011),Gasem(2001)温度函数对C8～C16之间的烷烃蒸汽压的预测结果的平均相对偏差小于3%。Coquelet (2004)和Robinson-Peng (1978)温度函数对C16以上烃类蒸汽压的预测结果最准确，平均相对偏差小于2%。由于汪萍等(2004)温度函数的参数关联式用C1～C16正构烷烃的实验蒸汽压数据拟合，对于22种正构烷烃的预测结果最准确，平均相对偏差为1.43%，其次为Robinson-Peng (1978) (1.86%)， Gasem (2001),Coquelet (2004)、Li-Yang (2011)、Haghtalab (2011)、Le Guennec (2016)、Forero (2016)、Twu-Mahmoodi(2017)、Coquelet-Mahmoodi (2017)、PR-PM (2017)和PR-PM2(2017)温度函数对正构烷烃蒸汽压的预测结果介于2.05%～2.47%，预测结果接近。

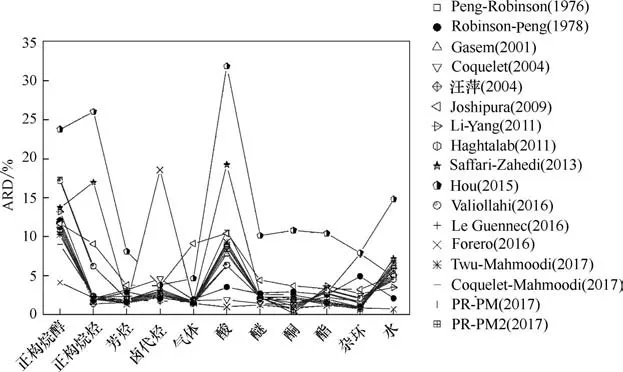
图1 参数普遍化温度函数对不同类别物质蒸汽压预测结果的平均相对偏差Fig.1 ARDs of vapor pressures for different kinds of compounds with generalized alpha functions

以正丁烷为例，研究各温度函数对蒸汽压的预测偏差随对比温度的变化趋势(图3)。除Joshipura(2009)和Hou (2015)温度函数外，其他温度函数在0.6≤Tr＜1 温度范围内对正丁烷的预测结果都比较准确，相对偏差小于±1%；当Tr＜0.6 时，随着对比温度的下降，温度函数的预测结果相对偏差迅速增大，最高可达到15%。由此可见，对于烷烃等非极性物质，普遍化温度函数对较低温度和较小压力下蒸汽压的预测偏差较大，在应用时要注意温度函数的应用范围。

总的来看，汪萍(2004)、Robinson-Peng (1978)、Gasem (2001)、Coquelet (2004)、Li-Yang (2011)、Haghtalab (2011)、Le Guennec (2016)、Forero (2016)、Twu-Mahmoodi (2017)、Coquelet-Mahmoodi (2017)、PR-PM (2017)和PR-PM2 (2017)温度函数对正构烷烃蒸汽压的预测结果都比较准确。

3.3 正构醇的预测结果

17 种普遍化温度函数对醇类物质蒸汽压预测结果的平均相对偏差见图4。从图4中可以看出，普遍化温度函数对醇类物质蒸汽压的预测结果偏差明显较大。Saffari-Zahedi (2013)和Hou (2015)温度函数预测结果偏差的变化趋势先略减小至平缓而后显著增大，平均相对偏差分别为13.79% 和23.84%，其中Hou (2015)温度函数预测结果的偏差最大。Forero (2016)温度函数对醇类物质蒸汽压的预测结果最准确，平均相对偏差为4.16%，显著优于其余温度函数。Forero (2016)温度函数对碳数小于C8醇类蒸汽压预测结果的平均相对偏差小于4.2%，但对正壬醇和正十四醇的预测结果偏差较大，平均相对偏差分别为10.92%和10.78%，对正癸醇、正十二醇、正十六醇和正十八醇蒸汽压预测结果的平均相对偏差介于2.18%～6.90%。除Saffari-Zahedi(2013)、Hou (2015)和Forero (2016) 3 种温度函数外，其余温度函数对醇类物质蒸汽压预测结果的偏差均呈现先增大后减小的趋势，且预测结果的偏差接近，平均相对偏差介于9.07%～17.38%。

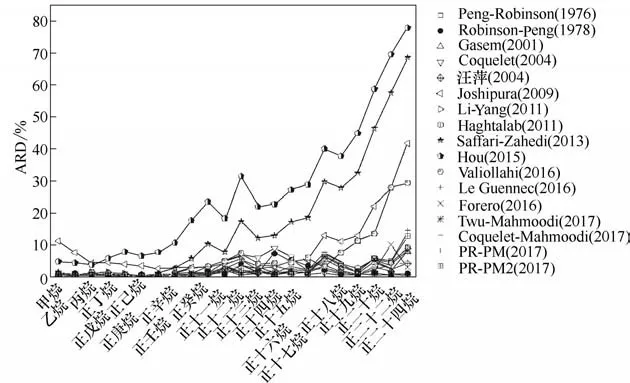
图2 参数普遍化温度函数对正构烷烃蒸汽压预测结果的平均相对偏差Fig.2 ARDs of vapor pressures for normal alkanes with generalized alpha functions

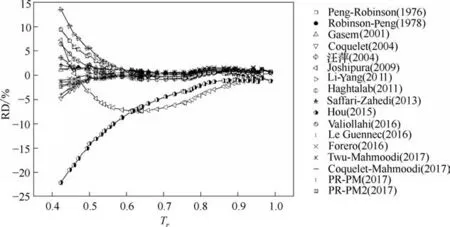
图3 参数普遍化温度函数对正丁烷蒸汽压预测结果的相对偏差随对比温度变化趋势Fig.3 RDs of generalized alpha functions on prediction of vapor pressures of n-butane with increasing reduced temperature

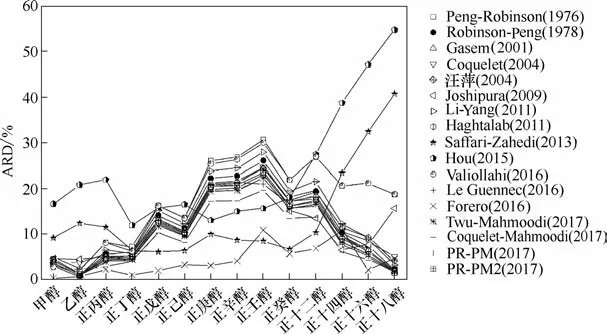
图4 参数普遍化温度函数对正构醇蒸汽压预测结果的平均相对偏差Fig.4 ARDs of vapor pressures for normal alcohols with generalized alpha functions

为了进一步分析普遍化温度函数对醇类物质预测结果偏差较大的原因，以正丁醇为例，观察蒸汽压预测结果的相对偏差随温度变化的趋势(图5)。Forero (2016)温度函数对正丁醇蒸汽压预测结果在Tr=0.525～0.993温度范围内偏差较小，相对偏差最大值为2.87%；Peng-Robinson (1976)等温度函数的预测结果在Tr＜0.7 的低对比温度范围内显著增大，偏差最大值达60%。Saffari-Zahedi(2013)温度函数对正丁醇蒸汽压的预测结果比较准确，平均相对偏差为6.52%。Saffari-Zahedi (2013)温度函数对正丁醇至正十二醇的蒸汽压预测结果优于除Forero(2016)以外的其他温度函数。

总的来看，普遍化温度函数对醇类物质蒸汽压的预测结果均较大，只有Forero (2016)温度函数的预测结果较准确。通过分析温度函数参数关联式可以看出，Forero(2016)温度函数是以偏心因子和极性因子为变量，通过极性因子校正Tr＜0.6 温度范围蒸汽压的变化趋势，提高了对低对比温度蒸汽压的预测精度。Valiollahi(2016)温度函数以对比密度为变量普遍化温度函数的参数，虽然普遍化方法改进，但不适用于醇类等极性物质蒸汽压的预测。除上述两种温度函数外，PR-PM (2017)等温度函数均采用偏心因子对参数普遍化。由此可见，仅用偏心因子普遍化温度函数参数的方法不适用于醇类等极性物质蒸汽压的预测。

3.4 芳烃、卤代烃、气体和杂环类物质的预测结果

普遍化温度函数对芳烃的预测结果比较准确，优于正构烷烃的预测结果，这是因为参与评价的芳烃类物质的分子较小，分子最大的1-甲基萘也仅含有11 个碳。比较普遍化温度函数对芳烃蒸汽压的预测结果可以看出(图1)，Forero (2016)温度函数对芳烃蒸汽压预测结果的偏差最小，平均相对偏差为1.40%，其次为PR-PR(2017)、PR-PM2(2017)和汪萍(2004)，分别为1.64%、1.69%和1.69%。Hou (2015)温度函数的预测结果偏差最大，平均相对偏差为8.14%，其次为Joshipura(2009)和Coquelet(2004)，分别为3.82%和3.19%。其余温度函数预测结果的平均相对偏差介于1.83%～2.93%之间。

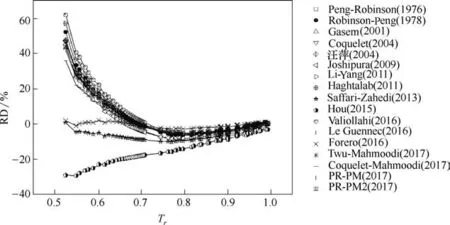
图5 参数普遍化温度函数对正丁醇蒸汽压预测结果的相对偏差随对比温度的变化趋势Fig.5 RDs of generalized alpha functions on prediction of vapor pressures of n-butanol with increasing reduced temperature

比较图1 普遍化温度函数卤代烃蒸汽压的预测结果可以看出，只有Forero (2016)温度函数预测结果的偏差最大，高达18.62%。Haghtalab (2011)温度函数预测结果的偏差最小为1.83%，其余温度函数的预测结果接近，平均相对偏差介于2.09%～4.67%。

普遍化温度函数对小分子杂环类物质的预测结果比较准确，Forero(2016)、Twu-Mahmoodi(2017)、Coquelet-Mahmoodi (2017)、PR-PM (2017) 和PRPM2 (2017)预测结果的平均相对偏差均小于1%。比较普遍化温度函数对气体蒸汽压预测结果比较准确，除Joshipura (2009)和Hou (2015)温度函数，其余温度函数对气体蒸汽压预测结果的偏差介于1.4%～2.0%。

3.5 醚、酮、酯、酸类物质的预测结果

17 种普遍化温度函数对弱极性的醚、酮、酯类物质蒸汽压的预测结果比较准确。Hou(2015)温度函数对蒸汽压预测结果的偏差最大，平均相对偏差分别为10.21%、10.86%、10.48%。其次Joshipura(2009)的偏差较大，平均相对偏差分别为4.47%、3.71%、3.35%。对醚、酮、酯类物质预测结果最为准确的是Forero (2016)温度函数，平均相对偏差分别为1.31%、0.84%、1.22%。其次为Coquelet (2004)温度函数，平均相对偏差分别为1.48%、1.31%、2.79%。其余温度函数对醚、酮、酯类物质蒸汽压的预测结果介于0.7%～3.7%之间，预测结果接近。

普遍化温度函数对酸类物质的预测结果偏差较大，主要误差来源于乙酸。普遍化温度函数对乙酸蒸汽压预测结果的最大偏差约为丙酸的10 倍。由于乙酸分子之间存在强缔合作用，其性质与丙酸、醇类等物质性质产生明显的差异。难以用偏心因子普遍化的单参数或两参数温度函数准确预测其蒸汽压。大多数温度函数对醇类物质蒸汽压预测结果的平均相对偏差在9%左右。其中以偏心因子和极性因子普遍化的Forero(2016)温度函数对酸类物质蒸汽压的预测结果最准确，平均相对偏差为1.07%，其次为Coquelet (2004)温度函数，平均相对偏 差 为1.98%，Robinson-Peng (1978) 和Peng-Robinson (1976)预测结果的偏差分别为3.58%和6.41%。Saffari-Zahedi(2013)和Hou(2015)温度函数预测结果的偏差最大，分别为19.31%和31.94%。

3.6 水的预测结果

普遍化温度函数对水蒸气压预测结果的偏差较大。只有Forero(2016)温度函数对水蒸气压的预测结果小于1%，为0.77%。其次为Robinson-Peng(1978)，平均相对偏差为2.15%，Li-Yang (2011)温度函数的预测结果为3.55%。Le Guennec (2016)、Twu-Mahmoodi (2017)、Coquelet-Mahmoodi (2017)、PR-PM (2017)和PR-PM2 (2017) 5 种新普遍化温度函数预测结果的平均相对偏差均在6%左右，偏差较大。由此可见，仅用偏心因子普遍化的温度函数对水等极性物质蒸汽压预测结果的偏差较大。

4 结 论

11 类70 种物质的4453 个实验蒸汽压数据对适用于PR EoS 的17 种普遍化温度函数的预测能力进行了评价，结论如下：

(1) 以偏心因子和极性因子普遍化的Forero(2016)温度函数对11类物质预测结果的平均相对偏差最小，为3.09%；对醇、酸、醚、酯、水等弱极性和极性物质蒸汽压的预测结果的平均相对偏差分别为4.16%、1.07%、1.31%、1.22%和0.77%，明显优于以偏心因子普遍化温度函数的预测结果。Forero(2016)温度函数对烷烃、气体和杂环类物质蒸汽压的预测精度与以偏心因子普遍化温度函数的预测结果接近，但不适用于卤代烃蒸汽压的预测。

(2) 汪萍(2004)和Robinson-Peng (1978)温度函数对正构烷烃蒸汽压预测结果的平均相对偏差分别为1.43%和1.86%，Li-Yang(2011)对氮气、一氧化碳、氨等气体预测结果的平均相对偏差分别为1.45%。PR-PM (2017)对芳烃预测结果的评价相对偏差为1.64%，仅次于Forero (2016)温度函数。Haghtalab (2011)对卤代烃的预测结果最准确，平均相对偏差为1.83%。

(3)仅以偏心因子普遍化的温度函数能够准确预测非极性和弱极性物质的饱和蒸汽压，但对极性物质饱和蒸汽压的预测结果偏差较大。对适用于极性物质的温度函数普遍化，需要表征极性性质的极性因子、偶极矩等特性参数参与拟合，以提高极性物质蒸汽压预测结果的准确度。

符 号 说 明

ARD——平均相对偏差

a——引力项参数

EoS——状态方程

P——蒸汽压，kPa

PR——Peng-Robinson

RD——相对偏差

RK——Redlich-Kwong

SRK——Soave-Redlich-Kwong

T——温度，K

α——引力项中的温度函数

ρ——密度，kg·m-3

ω——偏心因子

上下标

c——临界性质

exp——实验值

sat——饱和状态

r——临界参数的对比态