一种适用于泛克里金趋势函数的优化方法∗

杨金璇 潘 懋 刘钰洋 雷征东 吴耕宇

（1.北京大学地球与空间科学学院造山带与地壳演化教育部重点实验室 北京 100871）

（2.北京大学石油与天然气研究中心 北京 100871）（3.中国石油勘探开发研究院 北京 100083）

1 引言

近几年，三维地质属性建模中的确定性建模被广泛应用在油气勘探、开发等领域。确定性建模由储层地震学方法、储层沉积学方法和地质统计学克里金插值方法组成［1］。地质统计学方法根据待估点周围的若干已知信息，应用变异函数对待估点未知值做出无偏最优估计。目前广泛应用于空间域或时间域自然变量的定量化描述等众多领域［1］。简单克里金和普通克里金应用最广泛［2］，但先验条件严苛，大部分地质数据都难以满足，因此这两种方法的插值效果难以保证。

泛克里金插值是处理随机变量非平稳插值问题的方法，结合地质变量在一定范围内的变化规律进行建模，并且没有严苛先验条件，适用于绝大部分非均质性比较强的储层。杨功流［5］等对泛克里金插值方法和普通克里金插值方法进行对比研究，一方面在非平稳的地磁场数据的插值处理中应用两种方法，另一方面对比两种方法的插值效果。实例验证结果显示，使用泛克里金插值得到的地磁图更加符合地磁场的特征，证明对非平稳地质数据插值问题，泛克里金方法更适用。

然而，在广泛的实际应用中，泛克里金方法的理论优势并不明显。相较于其他简单快速算法，其精度优势比较微弱。目前，对于泛克里金插值精度的研究已成为热点。李龙［6］结合回归分析，应用泛克里金插值方法对大气参数进行插值，获得更高精度的AOD融合效果。王长虹等［8］在岩土参数随机场分析中，将泛克里金插值方法与多重分型理论相结合，度量局部空间的奇异性。赵爱梅等［11］研究泛克里金插值效果对变异函数的敏感性。何涛等［12］基于泛克里金插值的时间复杂度，研究趋势函数参数的估计。

本文考虑，对于泛克里金方法的使用前提是样品点数据满足正态分布，但是对于泛克里金方法来说，其插值结果依赖于反应地质变化规律的趋势函数，而满足正态分布不能保证研究区数据具有一定变化规律，即无法保证趋势函数的精度。本文对于趋势函数的模拟建立在残差分析的基础上，对样本数据进行重采样，提高插值样品数据的相关性及结构性，切合泛克里金方法的本质。

趋势函数是泛克里金插值方法中用于表达地质变量变化趋势的函数［4］，趋势函数的精度直接影响插值结果的空间性和随机性，甚至插值结果的有效性，因此趋势函数的拟合是泛克里金插值过程中最重要的问题之一。传统的趋势函数拟合建立在简单的多元线性函数拟合的基础上，本文提出，在传统拟合趋势函数的基础上，应用残差分析，将在95%置信度下判别为异常点的实验点剔除，将提升趋势函数的拟合精度。

2 数学原理介绍

2.1 泛克里金方法概述

泛克里金方法是一种线性无偏最优的空间插值计算方法，研究的非平稳区域化变量，包括趋势与残差两个部分，其数学表达如下：

式中，m(x)是趋势函数，R(x)是残差。趋势函数表示区域化变量在研究区内的某种明确的变化规律，是随机变量Z(x)的期望，有：

残差是表示趋势函数波动情况的局部量，是随机变量在趋势附近摆动的随机误差。在理论上，其期望值为零，且满足二阶平稳条件。

在泛克里金方法中，对于估计值的估计，就转化为对m(x)与R(x)的估计。对于趋势函数，可以用多元线性函数对其进行拟合。对残差的R(x)的估计，使用泛克里金方程组进行求解，即：

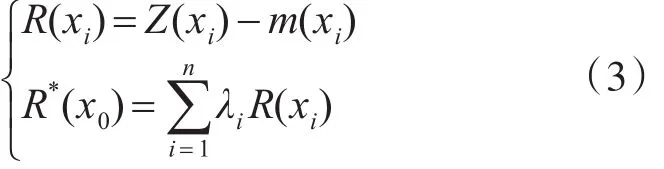
式中，R*(x0)是待插点的最优估计值，R(xi)表示已知样品的残差计算值，λi表示R(xi)的泛克里金权重系数。

泛克里金的目标函数为

式中，γ是变异函数。

变异函数γ是度量随机变量空间相关性的工具，在泛克里金插值方法中有重要意义［3］。实验变异函数是两个样品点的函数，公式如下：

式中，h是滞后距，γ*(h)为实验变异函数，N(h)为滞后距为h时的点对数，R(xi)与R(xi+h)是实验点xi和 xi+h的残差值，i=1，…，N(h)。

变异函数模型刻画实验变异函数值与滞后距的相关关系。球形模型是地质统计学中最常用的变异函数模型，本文选用球形模型进行计算。表达公式如下：

式中，c0是块金值，c是基台值，a是变程。

对式（6）分别关于ul和λi求导，并令其等于0，组成泛克里金算法的方程组。待插点的估计值正是通过解矩阵形式的方程组获得的。

2.2 残差分析基本原理

在统计学中，残差是指在回归分析中的实际观察值与回归估计值之差。可以理解，有多少对数据，就有多少个残差。通过残差所提供的信息，分析出数据的可靠性、周期性或其他干扰称为残差分析。

残差分析的基本原理：残差遵从正态分布N(δ，σ2)；δ与 σ 之比称为标准化残差，以 σ*表示；σ*遵从标准正态分布N(0，1)。若实验点的标准化残差落在置信区间以外的概率小于等于0.05，则称可在95%置信区间将其判别为异常实验点。

置信区间是指由样本统计量所构造的总体参数的估计区间［17］，展现的是这个参数的真实值有一定概率落在测量结果的周围的程度，其给出的是被测量参数的测量值的可信程度。通俗来讲，置信区间反映的是一种规律，当不断改变样本的时候，有95%的机会，真实值落在置信区间里，而不仅仅局限在特定样本。

在拟合趋势函数部分，利用置信区间的残差分析，可以帮助我们去掉预测值正确率小于0.05的样本，增加趋势函数的结构性和稳定性，以此达到提升插值效果的目的。这与泛克里金方法的适用条件是相一致的，即研究区域地质变量的变化有一定规律性，且可用简单函数进行模拟。

2.3 泛克里金插值技术路线

插值的样品数据是一系列已知具有某种属性和三维空间坐标的点，这些三维属性点来源于钻孔上的样品数据。整体建模流程分四步（图1（左）），步骤二和三是为插值提供已知信息和目标信息，步骤三的实现是本文的研究重点，可以进一步划分为5个步骤（图1（右））。残差分析应用在对趋势函数的拟合上，趋势函数的对R(x)的计算至关重要。

图1 插值建模流程

3 基于残差分析拟合趋势函数

一般情况下，泛克里金插值方法的使用前提为数据满足正态分布［3］。在地质中，数据满足正态分布并不能代表数据在研究区具有一定的变化趋势［14］，不代表可以用数学函数或模型对趋势进行表达。由此，对于进满足正态分布，但对趋势函数没有进行一定处理的泛克里金插值，其效果是不能保证的。

3.1 拟合趋势函数

根据泛克里金方法的应用要求，实验数据的空间分布必须满足正态分布。因此，使用泛克里金方法的第一步是对数据进行正态分布检验。对实验数据进行正态分析，在空间数据满足正态分布的前提下，可基于泛克里金方法基本原理及变异函数拟合方法，对数据进行空间变异结构分析，绘制实验变异函数曲线图，并根据变异函数的理论模型拟合实验变异函数。

趋势函数表达研究变量与空间坐标的相关性的线性程度，趋势函数的精度直接关系到R(x)的准确度。如果R(x)的计算结果不准确，插值结果将无意义。在多数情况下，地质变量的变化趋势都可以用一阶多元线性函数进行模拟［13］。本文选用一阶多元线性函数对趋势进行模拟。

3.2 对趋势函数进行残差分析

基于之前拟合出的趋势函数，对实验数据进行回归分析，计算出所有点对数据的残差和其对应的95%置信区间。用Matlab画出残差分析图，奇异点的定义为置信区间不包含0的点。按照定义，将奇异点剔除。对剔除奇异点的实验数据再次进行回归分析，验证奇异点已被剔除，实验数据在95%的置信区间内符合趋势函数。

3.3 插值准备

基于已知采样点属性值和拟合出的趋势函数，按照式（3），计算出各采样点的R(xi)。按照定义，R(x)为期望为0，协方差存在且平稳，且只依赖于两点之间的相对距离，与绝对位置无关的变量。估计待插点的R*(x)，则要按照克里金插值的步骤。首先计算实验变异函数值，量化数据间的相关关系，选择变异函数模型，得到最终变异函数。具体步骤如下：

1）对得到的样品数据进行空间性量化，根据空间位置坐标计算数据点对的欧氏距离；

2）按照距离对数据进行排序分组，计算每组的实验变异函数值；

3）在h-γ*(h)图（图8）上标出各点 (h，γ*(h))，得到实验变异函数大致走势图；

4）选取拟合相关系数较高的球行变异函数理论模型，应用线性规划法求解变异函数模型中的各个参数；

5）推断出一个统一的、由各向同性的结果表达式，得到最终的变异函数。

得到变异函数，便可计算协方差，进行泛克里金方程组求解，计算R*(x)的λi权系数。计算得到全部待插点的R*(x)，可按照式（3）得到全部待插点的估计值，以完成插值全过程。

4 实例验证

本节对某油田解释的测井数据进行孔隙度的泛克里金插值，共152口井，19508个采样点，层厚95m，南北方向17772.38m，东西方向15230.5m。将采用本文方法进行插值的结果与未去奇异点的泛克里金方法的插值结果进行统计量对比和交叉验证对比。

在实际建模中，首先建立结构模型，表达地质体表面的情况；生成网格模型；拟合趋势函数，计算变异函数；求解泛克里金方程组，计算全部待插点的估计值（见图2）。

图2 实验数据平面分布图

4.1 实验数据检验

通过研究区孔隙度的统计特征分析结果（图3），可以确定研究区的孔隙度数据符合正态分布，满足泛克里金方法的应用要求。

图3 数据分析直方图

4.2 拟合趋势函数

本文使用多元线性函数进行拟合，得到拟合度为0.42的趋势函数：

m(x，y，z)=-0.079x+0.21y+0.147z+9.39 （7）

对去除奇异点之后的实验数据再次进行多元线性拟合趋势函数，得到拟合度为0.74的趋势函数：

m(x，y，z)=-0.081x+0.18y+0.14z+9.09 （8）

为验证去奇异点效果，再次进行回归分析，得到残差分析结果（见图5）。

图4 采样数据残差分析图

图5 去奇异点残差分析图

4.3 变异函数拟合

本文选用球形模型来拟合变异函数，得到块金值为2831.33，基台值为9857.28，变程为1768.57。

4.4 插值计算

泛克里金插值方法的最后一步是计算插值结果，基于前文的各项计算和拟合出的函数，根据公式，计算得到待估点周围相关样品数据的权重值，并进行加权求和，计算出待估点的估计值。对全部待估点重复以上步骤，可以获得全部待估点的属性值，最终形成连续的三维地质属性模型。

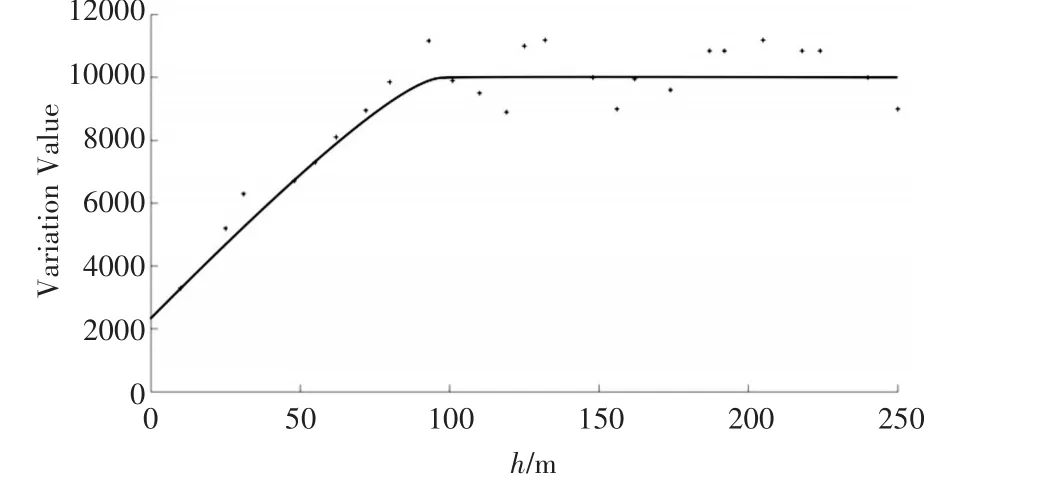
图6 变异函数图

4.5 结果与分析

4.5.1 统计量分析

比较统计量的方法表达数据的稳健性和分布情况是评价估计量好坏的基本方法［15］。T1、T2、T3分别是期望、方差和协方差。统计量如下：

从期望和方差的角度出发，期望越接近真实值，无偏性越好，方差越小，有效性越好，协方差用于衡量两个变量的总体误差［18］。在此为比较采样数据和本文方法的差异，以及采样数据和未去奇异点的泛克里金方法的差异，分别计算以采样数据为Z(xi)，以本文方法和泛克里金方法为Z(yi)的协方差。

由表1可知，由本文算法所得到的插值结果的统计量结果与采样数据的期望较接近；相较于未去奇异点的克里金，本文方法的方差更小，且更接近于采样数据方差，反应本文插值结果表达的地质变化规律更加平稳，与采样数据反映的地质变化规律具有一致性。由此可证，去奇异点对插值效果的有效性是有意义的。

表1 统计量结果

4.5.2 交叉验证

交叉验证是指在插值过程中，去掉一个或一部分样品点，对去掉的样品点处进行插值，并将插值结果与样品点处原有值进行对比，以验证插值结果的准确性［18］。对本文方法和未去奇异点的泛克里金方法进行全部样品数据的交叉验证，结果为表2。可以看出，本文方法的均方误差小于未去奇异点的交叉验证结果。由此可知，本文方法具有更高的准确率。

表2 交叉验证结果

5 结语

本文介绍了泛克里金和残差分析的基本原理，并介绍了泛克里金插值的技术路线，并指出本文的研究意义在于提升整体泛克里金插值效果。本文利用测井解释的孔隙度数据，对本文方法和未去奇异点的泛克里金插值方法进行分析，得出以下结论。

1）通过对实验数据趋势函数进行残差分析，得到对实际地质变量变化规律更高精度的数学表达，为建立有效精确的三维地质属性模型提供理论指导。

2）将本文方法应用到实际测井解释的孔隙度数据，获得合理有效的插值结果。将本文方法的插值结果与未去奇异点的泛克里金插值结果做统计量对比，结果表示本文方法插值结果的统计量结果更优，证明去奇异点对插值效果的有效性是有意义的。

3）对本文方法与未去奇异点的泛克里金插值结果进行交叉验证，本文方法交叉验证的结果的平均误差和均方根误差均小于未去奇异点的泛克里金，证明本文方法的插值效果的真实可靠性高于未去奇异点的泛克里金的插值效果。

4）研究得到的趋势函数模拟方法适用于所有针对带趋势的地质建模方法，因此可以应用于矿产资源预测、储层油气预测与评价等多个地质领域。