一种基于正六边形网格的数据安全聚合方案

归奕红

（柳州职业技术学院，广西 柳州 545006）

关键字：无线传感器网络；加法同态加密；数字签名；移动基站

0 引言

无线传感器网络（Wireless Sensor Network,WSN）由数百乃至数百万个传感器节点组成，能够实时地监测、感知网络覆盖区域中各种监测对象的信息，并将处理后的数据通过无线多跳的方式发送给用户。具有成本低廉、部署方便、可靠性高等优点，被广泛应用于军事侦察、国防安全、环境监测、医疗健康、智能建筑等各个领域。

由于传感器节点受到成本、体积和功耗等因素的限制，其电池容量有限；WSN 通常以较大数量部署在敌对或条件恶劣的环境中，更换电池是不现实的事；而上述环境对WSN 系统的安全性和检测数据的完整性、可用性都有较高的要求，这些要求意味着需要更大的能耗。节约能耗最有效的方法是进行数据聚合[1]，目前很多研究都集中在设计低能耗、高安全性的方案。

TinySec[2]是当前WSN 数据通信安全的事实标准，使用链路层加密确保端到端的通信安全，但数据必须在每一跳节点处被解密，再进行聚合，加密和解密操作过多，降低了网络的能效，而且基于私钥加密会导致密钥分配、密钥管理等问题，且没有提供数据完整性和可用性。

文献[3]在数据聚合时，使用秘密同态实现数据隐蔽，该算法采用对称密钥只提供了数据的机密性。

本文提出一个基于六边形网格的数据安全聚合方案（Data Security Aggregation scheme Base on regular Hexagonal cells,DSABH），该方案不仅实现网络无重复、无缝覆盖，还确保数据的机密性、完整性和可用性。

1 DSABH网络模型

1.1 节点类型

网络中有三种类型的传感器节点：检测节点、簇头节点、基站（sink 节点）。检测节点是一种资源非常有限的传感器节点，只具有环境感知、数据采集、简单运算和数据传输的能力；簇头节点是一种资源较丰富的传感器节点，具有数据接收、数据验证、数据融合的能力，并负责将数据向sink节点转发；sink节点是一种数据收集节点，具有大容量的数据存储、可更新的能源、可移动并与簇头节点通信等能力。

1.2 网络模型

在DSABH 方案中，根据传感器节点的传输能力，网络区域以若干大小相等的正六边形网格进行划分，每个网格作为一个簇（如图1 所示）。采用这种网格划分方法基于最优网络覆盖[4]：用感知半径为R 的圆，以其内接正六边形对区域进行覆盖，可以得到重复面积最少的无缝覆盖；基于正六边形覆盖模型所做的区域覆盖，除了网络的边界，任一节点与其周边6个节点所覆盖的区域是无缝覆盖，以此可推广到整个网络区域。该模型可以保证网络以最少的节点数实现通信覆盖和连通覆盖，从而达到节能的目的。

簇区域一旦形成，在整个网络生命周期内都不会再重新划分。检测节点随机地部署在监测环境中；簇头节点则根据簇区域的大小，利用智能技术（如小型飞行器及定位技术）均匀地散布在各簇中，每个簇可以根据需要设置2-5 个簇头节点，任一时刻只有一个簇头工作，其它簇头节点休眠；sink节点可以移动，其运动方向和运动速度都是可控的，其数据收集方式是周期性循环进行。

2 DSABH密钥管理

DSABH 方案采用端到端安全机制----同态加密技术对数据进行加密，数据在到达基站之前一直保持密文状态，簇头节点可以对密文直接进行融合操作，避免数据被恶意节点窃取或篡改。

2.1加密算法

在WSN 中，为了确保数据传输的机密性，数据通常需要经过加密后传输。传统的对称密码算法轻量，适合资源受限的WSN，但容易被破解；非对称密码算法安全性强，但计算量大，容易造成传感器节点能量的过度消耗；采用基于公钥机制的同态加密技术，可以在不解密的情况下，直接对密文数据计算聚合结果，有效地减少了节点的能量消耗，适合作为WSN的加密算法。

DSABH 方案采用加法同态机制，确保两个数据加密后的计算（加法）结果与先计算（加法）再加密的结果一致，即：E(m1)+E(m2) = E(m1+m2)。数据在检测节点处利用sink 节点的公钥进行加密后，传输给簇头节点；簇头节点对收到的多个密文数据进行加法运算，其值作为聚合结果，经过多跳、多次聚合传输到sink节点；最后由sink节点对密文进行解密。任何入侵者、任何妥协节点由于没有sink 节点的私钥，即使获取到聚合信息也无从解密。

同态加密技术不能提供数据的完整性和可用性，因此DSABH方案加入了数字签名----使用公钥椭圆曲线密码进行加密，即能使用数字签名，但数字签名算法不具有同态特性，对两个数据进行签名无法得到数据的和。本文使用的签名算法是对基于椭圆曲线数字签名算法进行了扩展，并加入全局时钟，加入全局时钟的目标是为了提高数据传输的安全性、确保数据的可用性。

2.2 数据聚合过程

DSABH 方案的数据聚合过程如图2 所示：各检测节点感知环境数据，使用sink 节点的公钥进行同态加密（如E(x)），使用各自的私钥进行数字签名（如S(x)）；密文数据（包括数字签名及公钥）经过中间节点以多跳方式向簇头节点汇集，簇头节点对这些密文数据进行加法同态运算，然后沿路由到达sink 节点。如果中间节点或簇头节点自己也感测到数据，则该数据也同样进行数字签名、同态加密，相同的聚合过程在网络中重复进行，直至到达sink节点。

因为所有的感知数据和聚合数据都采用sink节点的公钥加密，所以只有sink 节点具有对聚合数据进行解密的能力；各检测节点和簇头对自己发出的数据采用数字签名，这些签名也进行加法聚合。因此，基站同样可以通过数字签名之和来验证数据的完整性，即数据是否由合法的节点发出且未经篡改。

图1 DSABHA算法簇结构

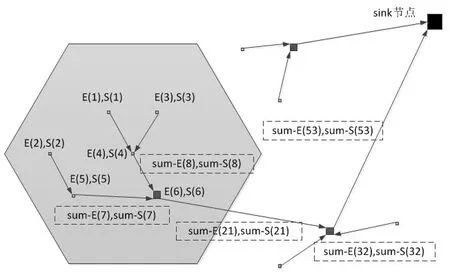
图2 同态加密数据聚合示意图

2.3 算法描述

在WSN 部署之前，所有传感器节点都预装了各自的私钥、sink节点的公钥、椭圆曲线参数，以及网络的全局时钟值t，t为整数且每经过一个固定时间就会自动更新，以此确保数字签名的安全性和可用性。当每轮传输数据开始，各节点将随机选择一个私钥d，私钥d 与椭圆曲线的基点G 相乘即得到相应的公钥D，该公钥为椭圆曲线上的另一个点。

2.3.1 数字签名算法

数字签名规则如下：节点Z对数据m进行数字签名，该签名为t-1(mz+dzr)，入侵节点可以侦听到该签名，也可以得知t-1和r的值，但无法破解mz和dz；如果节点Z使用相同的私钥对另一条检测数据进行数字签名，由于该检测数据的值可能不变，那么这种使用相同的私钥对相同的数据签名的做法，容易让入侵节点猜出该节点的私钥。因此，每一轮数据传输都需要生成新的私钥/公钥对。各节点生成自己的数字签名s的方法是作t mod n的乘法逆运算；数字签名生成之后，各节点对传输数据进行同态加密，再将加密后得到的数值映射到椭圆曲线C上，然后采用EC-IES算法[5]对该映射值进行加密，获得密文E(m)。

其详细算法描述如下：

节点Z的私钥/公钥对与下列参数有关：

C={FR, q,a,b,G,n,h}，其中C 是椭圆曲线，FR 是椭圆曲线的表示方法，q是椭圆曲线的阶，a、b是椭圆曲线的参数，G是椭圆曲线的基点，n是G的阶（n是一个大素数），h是非常小的辅因子。

步骤1：生成私钥/公钥对：在区间[1,n-1]中随机选择一个私钥d，计算获得对应的公钥D=dG；

步骤2：系统生成全局时钟随机数t，满足1≤t≤n-1；

步骤3：进行下列计算：tG=(x1,y1)、r=x1mod n、t-1mod n；

步骤4：计算得到s=t-1(m+dr)mod n，如果s=0则返回步骤2，否则继续；

步骤5：对数据m进行数字签名，结果为(r,s)；

步骤6：对数据m进行加法同态运算，结果为E(m)，则可知聚合后的密文为∑E(mi)，聚合后的数字签名为∑(ri,si)。

2.3.2 验证数字签名算法

Sink 节点收到密文聚合数据后，首先用其私钥对该密文进行解密；然后将椭圆曲线上的点到该密文聚合数据的映射作逆运算；验证签名是否合法：sink节点使用收到的组合签名（签名被包括在组合签名中）、已解密的聚合数据与全局时钟t，计算得到椭圆曲线上的一个点，如果该点的横坐标与r值相同，则可判定该数字签名来自合法节点。

其详细算法描述如下：

步骤1：如果r 和s 在区间[1,n-1]中，则继续，否则可判定该数字签名非法；

步骤2：通过私钥对密文聚合数据进行解密运算，获得明文m；

步骤3：进行下列计算：w=s-1mod n、u1=mw mod n、u2=rw mod n、X=u1G+u2D；

步骤4：如果X=0，则可判定该数字签名非法，否则继续计算v=x1mod n，其中x1为X 的横坐标；

步骤5：如果v=r，则可判定该数字签名合法，接受该签名。

如果解密后得到的t 值明显落后于当前时钟值，说明该数据为过时数据，不具备可用性，应当丢弃。

3 DSABH性能仿真及分析

3.1 安全性分析

本文提出的DSABH 方案是同态加密技术加上数字签名技术。同态加密技术的安全性早已被公认[6]；数字签名技术是对椭圆曲线数字签名算法的扩展----对数字签名进行组合，而椭圆曲线数字签名算法的安全性已经在相关研究中得到证实[7]，因此，本方案中数字签名的安全性只要能证明以下两点即可：第一，通过组合数字签名能判定单一数字签名是否由合法节点生成，即数字签名之和能生成一个有效的数字签名；第二，当且仅当所有为某一聚合结果提供数据的节点都为合法节点时，对该聚合结果的验证才会出现v=r。

证明一：已知m=m1+m2+……，s=s1+s2+……，且si=t-1(mi+dir)，则

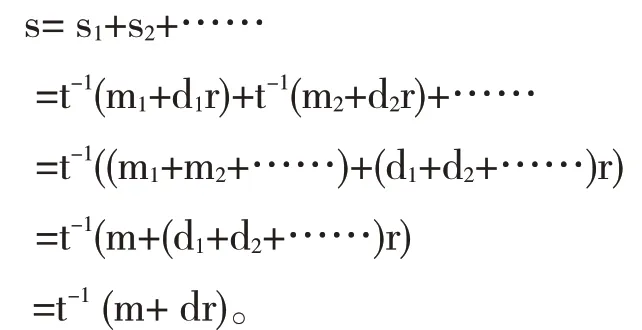
即数字签名之和产生一个有效的数字签名可证。

证明二：由X=u1G+u2D且D=dG，可得

X=u1G+u2D=u1G+u2(dG)=(u1+u2d)G

由于s=t-1(m+dr)，整理后可得

因此，X=kG，即(x1,y1) = kG，当所有节点都是合法节点时，由v=x1mod n可得v=r。

通过以上证明，可知本方案中采用的加密技术和数字签名都具有很好的安全性。

3.2 能耗分析

通过在TinyOS 中模拟实现相关协议，对本文算法与其它典型算法（如TinySec）的能量消耗进行对比。

建立仿真环境如下：在边长为500米的正方形场景中随机分布150 个传感器节点，其中20 个为资源较丰富的簇头节点，检测节点初始能量设置为1 焦耳，簇头节点初始能量设置为2.5 焦耳；各节点每2秒发送一次数据；检测节点的通信半径为20m，簇头节点的通信半径为60米；sink节点距离网络中心120 米，在DSABH 方案中，sink 节点以120 米为半径绕网络中心移动，移动速率为每100秒15弧度。

仿真在两种算法下分别运行10 次，取平均值，得到如图3所示结果：

图3 网络能耗比较

从图中可以看出，TinySec 方案由于数据必须多次解密/加密，增加了运算开销和能量消耗。而DSABH 方案中，发送节点进行一次加密和数字签名运算，中间节点不用解密，直接进行聚合运算并转发；且sink 节点采用移动的方式，避免了网络局部区域节点因频繁转发而造成能耗过大的问题，进一步均衡并节省了网络的能量消耗。因此，DSABH方案在能量消耗上表现出强大的优势。

4 结论

安全性和节能是WSN 重要的研究领域，直接影响到WSN 能否得到广泛应用。本文提出的DSABH 方案创新之处在于：利用同态加密技术为网络提供低能耗、强大的安全；将数字签名结合全局时钟应用于WSN，有效地抵御了非法节点的入侵，保证了数据的完整性和可用性；采用移动sink节点的方式均衡了网络各处的能量消耗，有效延长了网络的寿命。下一阶段的研究目标是继续关注大规模WSN 的安全，将自然免疫的方法应用到网络中，使其能够在整个网络生命周期中发挥全面的安全保护任务。