一种罗经方位对准的参数设置方法
马永轩,马仁冬,葛 磊
(1.沈阳理工大学 自动化与电气工程学院,沈阳110159;2.北京计算机技术及应用研究所,北京100854)
捷联惯性导航系统是一种航位推算系统,因此在进行工作前需要进行状态信息初始化,即需要确定捷联惯导系统的初始位置、速度和姿态矩阵。而确定初始姿态矩阵的过程即为惯导系统的初始对准。在众多的初始对准方法中,罗经对准方法参数设置简单、易于实现、计算量较小,是捷联惯性导航系统初始对准技术的研究热点。
近些年,有关罗经对准的相关研究较多,如文献[1]研究了旋转调制的罗经对准,通过旋转调制将陀螺常值漂移变换成正弦信号,再通过合理设置相关参数将其滤除,进而消除对对准精度的影响。文献[2]分析了随机游走对罗经方位对准的影响,并推导出了误差方差公式。文献[3]研究了姿态逆向解算的罗经对准。文献[4]研究了罗经方位对准的收敛时间,给出了相关误差的时域函数,为控制收敛时间提供了参考。
对于罗经对准的参数设置,文献[5]研究了基于最优模型的时变参数罗经对准算法,并利用遗传算法对大方位失准角条件下的罗经对准参数进行了优化。文献[6]提出了基于粒子群算法优化的捷联罗经初始对准方法,将航向角的收敛速度和收敛精度作为构建适应值函数的重要参考,将对准后半段的航向角误差、航向对准过程的超调量和上升时间以及水平姿态角误差分配不同权值并求和作为构建代价函数的最优指标,再利用粒子群优化算法搜索出最优罗经参数。文献[7]与文献[6]类似,只是采用了遗传算法作为参数寻优算法。
然而这一类参数设置方法的缺点是明显未考虑在实际的初始对准过程中相关误差的影响,如随机游走系数、初始方位误差、陀螺随机常值漂移对罗经对准的影响,其代价函数的选取也值得商榷,因此会严重影响此类方法的实用性。
基于以上原因,本文综合近年来罗经对准的相关成果,综合考虑罗经方位对准过程中所存在的误差源及各误差源对初始对准结果的影响,提出将罗经方位对准误差方差最小作为评价准则的参数设置方法;该方法综合考虑了主要误差源的影响,因此,具有较强的实用性。
1 罗经方位对准的误差源
罗经方位对准的原理及罗经回路设计可见文献[4],将罗经回路设计成四阶系统,则各项误差源在该四阶系统下的频域响应为
(1)
其中
(2)
以上符号的意义可参考文献[4]。一般的罗经回路设计为2个相同的二阶系统串联成的四阶系统,且特征根设置为s1,2=s3,4=-σ±jωd,且σ=ωd=2π/Td,则有
Δ(s)=((s+σ)2+ωd2)2
(3)
此时有K1=K4=2σ,K2=4σ2/ωs2-1,K3=4σ4/g,则在罗经方位对准中,所有参数都与二阶系统的阻尼振荡周期Td有关,只需设定Td值,其它参数也就相应确定。
由式(1)可知,影响罗经方位对准精度的共有5项:分别为北向加速度计零偏变化率▽N、东向陀螺漂移εE、东向角初始误差φx(0)、天向陀螺漂移εU和方位角初始误差φz(0)。然而,对于一般的惯导来说,在进行初始对准前,惯导都会进行预热,即使不预热也会进行惯性器件的温度补偿,因此,加速度计零偏变化率▽N,该项可忽略不计;对于东向角初始误差φx(0),当罗经对准经过水平调平后,这一项非常小,对罗经方位对准影响有限,也可忽略不计;而对于天向陀螺漂移εU,当Td设置较小时(1000s以下),对罗经方位对准影响较小,也可忽略。因此,主要影响罗经方位对准的有东向陀螺漂移εE和方位角初始误差φz(0)。然而式(1)中的误差源为常值,在实际初始对准过程中,还应该考虑东向陀螺随机漂移(主要表现为随机游走)的影响;根据文献[2]可知,随机游走对初始对准的影响是不可忽略的。因此,总结起来,罗经方位对准的主要误差源有三项,即东向陀螺常值漂移、东向陀螺随机漂移、初始方位误差,罗经方位对准的误差为这三项相加,即
φz(t)=φz0(t)+φz1(t)+φz2(t)
(4)
其中φz0(t)为东向陀螺常值漂移的对罗经方位对准影响的误差表达式,且有
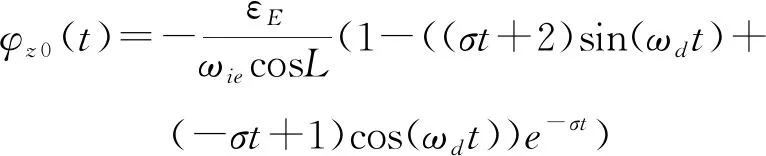
(5)
φz1(t)为初始方位误差对罗经方位对准影响的误差表达式,且有
(6)
φz2(t)为东向陀螺随机漂移对罗经方位对准影响误差,为一随机量,没有确定的表达式,只有方差来表示,即
(7)
式中q为随机游走系数。参考文献[4]可知,罗经方位对准的收敛时间与参数Td有关;在初始方位误差为5°、陀螺常值漂移为0.05°/h时,至多在1.4Td时间即可收敛到0.01°的误差带内。因此,假设对准时间为T时,如需初始方位误差和陀螺常值漂移的影响收敛,则Td的设置要小于T/1.4。然而,研究随机游走对罗经方位对准影响公式(7)可知,Td设置的越小,随机游走产生的误差方差则越大。因此,参数Td的设置,从收敛时间角度和随机游走对对准精度影响的两个不同角度考虑,参数设置是矛盾的。考虑初始对准快速收敛,则需要Td设置小一些;考虑随机游走的影响,则需要Td设置大一些。因此,想要得到最优的参数设置,则需综合考虑收敛时间和随机游走对对准精度的影响,对参数Td的设置有一个折中和平衡。
2 罗经方位对准的精度评价
惯性导航系统初始对准的精度评价,一般是以初始对准的方差作为精度评价指标,即在规定的对准时间T内,对准的方差越小,则对准精度越高。因此,在本文中,也以罗经方位对准的方差作为精度评价指标。本文在设置罗经方位对准的参数Td时,以罗经方位对准的方差最小作为目标,因此,需要建立参数Td与方差的函数关系。
一般来说,对于陀螺常值漂移,由于对惯性器件出厂前需要进行标定和补偿,部分陀螺常值漂移已经被补偿掉,而残余的常值漂移实际上是逐次启动的零偏重复性,该零偏重复性的大小可通过出厂前的测试统计出来。对于方位初始角误差,一般为粗对准的结果;对于多次对准来说,也是一个随机量,在惯性器件精度一定的条件下,粗对准精度也可以统计出来。因此,虽然φz(0)和εE在某一次对准中是确定性输入,但对于逐次启动初始对准来说,其为随机量,即每次启动时φz0(t)和φz1(t)是随机的,这里假设φz(0)和εE的方差分别为var(φz(0))和var(εE),则φz(0)和εE对罗经方位对准结果的影响是随机的。参考文献[2]可知,随机游走对罗经方位对准的影响也是随机的。因此,对于逐次启动进行初始对准的惯导,其对准结果为随机变量,这三项误差源对罗经方位对准的影响都是随机的,且由于这三项误差互相独立,因此总误差的方差为三项误差的方差相加,即
var(φz(t))
=var(φz0(t))+var(φz1(t))+var(φz2(t))
(-σt+1)cos(ωdt))e-σt)2+
var(φz(0))(((σt+2)sin(ωdt)+
(-σt+1)cos(ωdt))e-σt)2
(8)
3 罗经方位对准的参数设置方法
在工程应用中,往往对对准时间有要求,需要在规定的初始对准时间T内,设置参数Td,使得罗经方位对准的精度最高,即使初始对准的误差方差var(φz(T))最小,则在经过T时间的罗经方位对准误差方差var(φz(T))为
(-σT+1)cos(ωdT))e-σT)2+
var(φz(0))(((σT+2)sin(ωdT)+
(-σT+1)cos(ωdT))e-σT)2
(9)
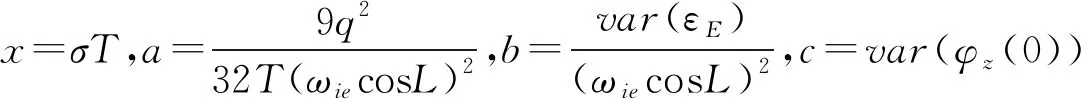
则式(9)可简化为
var(φz(T))=ax+b(1-((x+2)sinx+
(-x+1)cosx)e-x)2+c((x+2)sinx+
(-x+1)cosx)2e-2x
(10)
式(10)转化为a、b、c可求的条件下,求var(φz(T))的最优解x。
对于如式(10)的超越方程求最小值,从理论上来讲,是没有解析解的。因此,只能采用数值计算的方式求出最优解,如牛顿法、最速下降法、智能优化算法等。具体计算方法在这里不予赘述。
在计算条件不便的情况下,这里提供了一个次优解,令(x+2)sinx+(-x+1)cosx=0,从而解得x=3.574,则有
Td=2πT/3.574=1.758T
(11)
该次优解的优点是,不论a、b、c如何取值,Td的取值只与规定的对准时间长度T有关,而与a、b、c的取值无关。这样可以省却a、b、c取值不同时,对参数Td进行设置的麻烦,此时的方差为
(12)
此时即为忽略误差震荡项对罗经方位对准的影响时罗经方位的极限对准精度。
这里还需注意的问题是,在参数设置过程中,虽然能求得最优或次优解,但并不代表此时罗经方位对准已经收敛,实际上其误差曲线仍然处于未收敛的震荡状态,只是根据罗经方位对准误差曲线的震荡特性,在某个时间点求得了误差方差的最小值。因此如果在参数设置完成后,初始对准过程中刻意延长对准时间,则反而有可能使对准方差变大,对准结果变差。因此,当到达对准时间后,需立即停止罗经方位对准,并切换到导航状态。
4 数值仿真
一般在进行精度统计时,习惯用标准差来表示,即对方差开根号。由于方差都是大于0的数,选择Td使初始对准的方差最小时,也即是初始对准的标准差最小。因此,在仿真中,沿用传统的习惯,对各带有统计性质的误差参数都以标准差的形式来进行表示。
假设罗经方位对准中,三个姿态角为0°、0°、0°,纬度为39.91°,初始方位误差标准差0.5°,只有X陀螺有随机常值漂移标准差0.01°/h,随机游走系数为0.001°/h,初始对准时间T=300s,则根据式(10),可求得最优参数设置Td=537s。为此,进行500次的数值仿真,每次仿真时间600s,并对每一个对准时刻的方位角误差进行统计,求得其标准差,具体结果见图1所示。
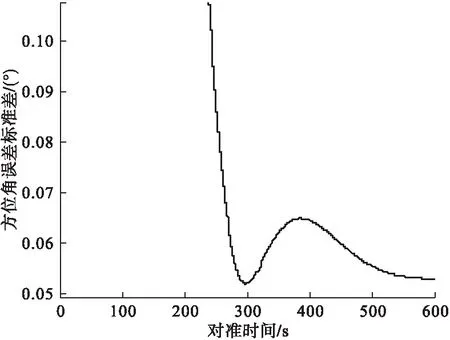
图1 方位角误差标准差曲线
由图1可以看出,初始对准的方差在298s取得最小值,不论在298s前还是298s后,其标准差都大于298s时的方差,即使对准时间达到了600s时,初始对准误差的标准差仍然大于298s时的标准差,可见,单纯的延长初始对准的时间,并不能有效的提高初始对准精度。对参数Td的选择,是十分重要的,尽管对准标准差最小值在298s比理论上的300s少2s;且标准差最小值为0.0518°,比理论最小值0.0523°小0.0005°,但仍可认为理论与实际仿真效果较为吻合,而这一误差产生的原因主要是数值仿真产生的随机数的方差不够准确导致。
为进一步验证本文所提方法的正确性,对于上述的仿真条件,设置Td=450、Td=600和由式(11)求得的次优解Td=527,分别进行500次仿真,再求误差标准差,并与最优解Td=537进行比较,仿真结果见图2所示。
从图2可以看出,不论参数大于还是小于最优解,在第300s时的初始对准标准差都小于最优解时的标准差;即使不在300s处取值,其最小值也小于Td=537的最小值,且设置的参数越接近最优解,误差标准差最小值越小,最小值越接近在300s时。观察次优解发现,虽然为次优解,但与最优解相差不大,因此在300s时的对准结果也较好。
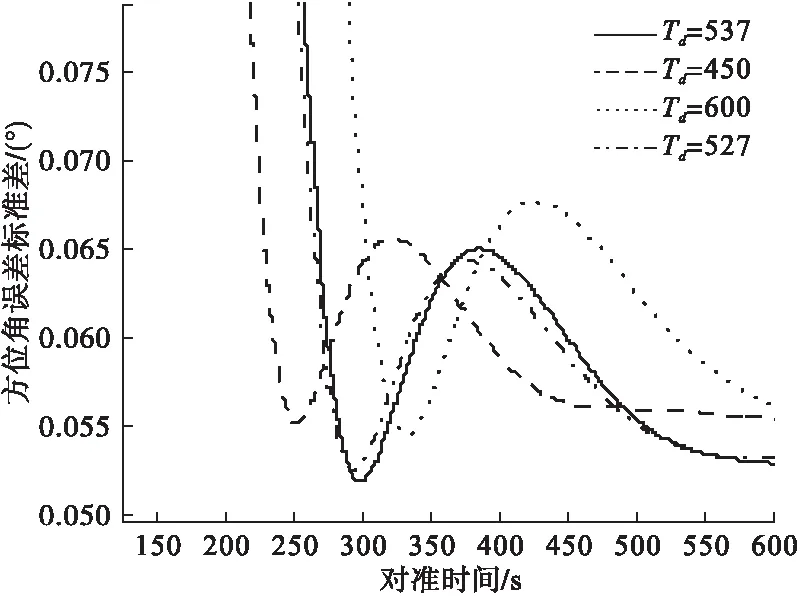
图2 不同Td的方位角误差标准差曲线
5 结论
在分析了罗经方位对准误差的基础上,提出了以对准误差方差最小为约束准则的罗经方位对准参数设置方法,将参数设置转化成为求取函数最小值的问题,并针对最小值与三个参数都相关的情况,提出了一个次优解,该次优解只与对准时间长度有关,与其它参数无关,可在牺牲一定精度的条件下,更加简便的设置参数。数值仿真验证了本文所提方法的正确性。

