基于NSGA-Ⅱ灌区两级渠道输配水优化调度

徐淑琴，高凯茹，乐 静，王亚超，乔厚清，王雅君

（东北农业大学水利与土木工程学院，哈尔滨 150030）

随粮食需求增加，全球农业用水量（包括旱地农业和灌概农业）增加[1]，但多地区淡水供应受多因素影响而减少，如气候变化、水质恶化及地下水超采等[2]。因此，提高水资源利用效率和效益，对实现社会经济持续发展具有重要意义。

灌区是我国农业用水主体，我国灌区设计灌溉面积占总灌溉面积85%以上[3]，对灌区渠系配水作科学决策，合理优化配置有限水资源，减小渠系输水损失，是缓解水资源供需矛盾、提高我国水资源利用效率及促进农业持续发展重要手段[4]。

灌区优化配水研究方法多为优化单目标函数[5-6]，从单一目标优化变成多目标优化。传统针对多目标优化问题的加权法、目标规划法等难以保证求解结果最优性，而遗传算法内在并行机制及全局优化特性使其在解决多目标优化问题时更适用[7]。遗传算法改进后提出VEGA[8]、NSGA[9]等方法。NSGA 保持个体多样性，避免超级个体过度繁殖造成早熟收敛，但种群个体数目较多时，计算复杂度较高，耗费时间长且难以保证满意解不丢失。基于NAGA存在问题，学者提出带精英策略非支配排序遗传算法，在选择算子执行前根据个体间支配关系分层，使其在Pareto 域上均匀分布并引入拥挤度及精英策略，提高运算速度、种群水平及优化结果精度[10]。本文采用带精英策略非支配排序遗传算法（NSGA-Ⅱ）优化灌区渠系水资源调度，分析模型可行性，为灌区科学配水提供依据。

1 带精英策略非支配排序遗传算法概述

1.1 带精英策略非支配排序遗传算法（NSGA-Ⅱ）

带精英策略非支配排序遗传算法（Non-dominated sorting genetic algorithms-Ⅱ,NSGA-Ⅱ）由Deb提出[10]。该算法是基于遗传算法对多目标问题优化求解方法，基于Pareto（帕累托）最优解讨论多目标优化。求解多目标优化问题时，由于目标间存在冲突，不能同时达到最优解，多目标问题存在一个解集，无法比较所有目标优劣，这些解集合称为Pareto（帕累托）最优解。NAGA-Ⅱ是在遗传算法基础上改进，基本原理：通过快速非支配排序程序将父代和子代种群结合产生优秀个体并根据适应度和扩展性创建交配池精英策略，共享参数设置，降低计算复杂度，防止丢失较优解。具体求解步骤如下[11]：

①编码。对所构建模型中决策变量（配水流量、配水时间等）作实数编码，由于二进制编码需种群个体较大且在收敛于全局占有前沿面上存在困难，故本文采用实数编码。

②种群初始化。对交叉概率、变异概率、迭代次数等运行参数作初始化，在解空间内产生N个个体初始种群P0，N个个体产生具有随机性，将这个随机创建初始种群作为亲代种群。

③产生第一代子群。将随机产生亲代种群根据非支配情况排序，即根据每个解非支配等级指定其对应适应度；对分层后个体执行二元竞赛选择、正态分布交叉、多项式变异等操作，不断重复上述操作直至新种群Q0产生，将Q0作为子代种群。

④生成新亲本种群。将规模同为N 亲代种群P0与Q0作合并组成种群规模为2N 临时种群R0，然后根据非支配度对种群R0排序，筛选所有复合要求解集合，通过拥挤度计算选择最优N个个体作为下一代亲本种群P1。

⑤当迭代次数达到之前预设最大值时，结束运算；否则，跳转到步骤③循环操作，直至满足条件。

1.2 模型构建

根据灌区渠系分布特征，将渠道分为干渠、支渠、斗渠，干渠、支渠为续灌渠道，斗渠则轮灌。本文以文献[12]中多目标优化模型为算例，构建干渠、支渠多目标遗传算法优化模型，既保证灌区渠道水流平稳，同时控制渠道输水损失。模型第一个目标函数是以干渠和支渠总损失最小为目标函数；另外为使各级渠道水位更好衔接，将配水过程中水流波动性最小作为第二约束目标。运用非支配排序遗传算法对干、支渠道渠系配水流量、配水开始时间、配水结束时间求解。目标函数：

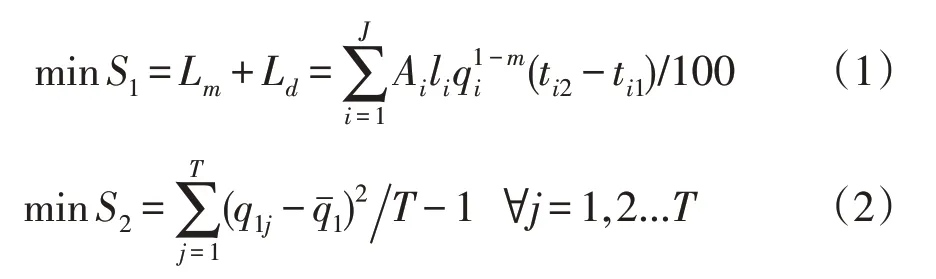
式中，Lm、Ld-干、支渠道输水损失量；J-渠道条数；i 为各级输水渠道编号；li-第i 条渠道长度；qi=-各条渠道实际配水流量（m3·s-1）；ti2、ti1分别代表渠道i 配水结束时间与开始时间（d）；A、m分别为渠床土壤透水系数、渠床土壤透水指数，参见文献[13]选取，灌区土壤为轻壤土，上述参数取值分别为2.65、0.45；j 为渠系输水不同时段，T 代表时间（d）；q1j代表上级渠道在不同时刻渠系配水流量（m3·s-1）；为0～1 变量，描述灌区内渠道配水状态，渠道配水时，f(t)=1，反之为0；qˉ1代表上级渠道各时段平均流量（m3·s-1）。

约束条件：

①流量约束灌区

渠系实际配水流量在渠系最小流量及加大流量间，渠道流量最小系数Jv、加大系数Jd选取参照文献[13]，一支渠取值分别为0.6、1.3，而干渠、二支渠取值则为0.6 与1.25。渠道实际配水流量即在渠道最小流量与加大流量范围内变化。

②地表水供水量约束

渠道配水流量与配水时间乘积应该在地表水可供水量范围内，Wmax为地表水最大供水量，Wmin为地表水最小供水量。

③水量平衡约束

灌区任意时刻下级渠道配水流量之和等于上级渠道实际配水流量：

④时间约束

灌区各级渠道配水结束时间与开始时间：

2 算法实例应用

2.1 灌区概况

富裕牧场位于松嫩平原西北部大兴安岭东麓丘陵区向平原过渡带，富裕县境内，行政区划隶属于黑龙江省农垦总局齐齐哈尔管理局，地理坐标为东经124°13'30''～124°46′57″、北纬47°36'45''～47°57′40″。富裕牧场地处黑龙江省西部温和农业气候区，在气候地理上属中纬西风区，是热量交换最大，南北气流交换最多，垂直环流较强区域。由于冷、热、晴、雨等变化频繁，形成寒温带大陆性季风气候。春季风大干旱，夏季热源充分易受洪涝，秋季凉冷短暂，偶遇早霜，冬季多风寒冷漫长是本区气候特点。

富裕灌区位于富裕牧场东部，范围北起引嫩总干渠，南至乌裕尔河一级阶地，西靠通南沟，东至八家子泄洪沟。研究区年平均气温3.22 ℃，全年有5 个月气温在0 ℃以下。1 月最冷，月平均气温-19.8 ℃；7 月最热，月平均气温22.6 ℃左右，极端最高气温40.7 ℃，极端最低气温-38.5 ℃；全年≥10 ℃有效积温多年平均为2 850 ℃，区内多年平均日照时数可达3 000 h。研究区各气象因子年内变化情况见图1。

富裕牧场有2条自然河流和1条人工河流在场区流过，2条自然河流分别是位于场区南部乌裕尔河及穿场而过的通南沟，而人工河则为北部引嫩总干渠。其中乌裕尔河是季节性河流，在枯水期常出现断流现象，无法保证灌溉用水；南通沟大部分均已开发垦殖，冬春季多断流，汛期洪水较大，为季节性河流。因此，富裕灌区主要供水来源为北部引嫩总干渠供水，不足部分开采地下水作补充。富裕灌区地形北高南低，东高西低，南北向地形比降约1/5 000，东西向地面比降约1/3 000，灌区内可实现自流灌溉。

富裕灌区共布置灌溉总干渠1 条，支渠2 条，总长14.99 km。灌溉渠道布置情况为：干渠从北引总干渠乌北段75+385 渠首进水闸开始，向南沿八家子泄洪沟在4+185 处穿过公路，全长4.24 km。沿线布设2 条支渠，位于干渠1+050 和4+240 处，分别为一支渠和二支渠。富裕牧场一支渠从总干渠1+050 处分水后由东向西沿截流沟方向延伸，长1.85 km。二支渠从总干渠4+240 处分水后，由东向西沿公路南侧延伸至通南沟，长8.9 km。其中一支渠下设3条斗渠，方向为南北向，总长7.02 km。二支渠下设10 条斗渠，方向均为南北向，总长22.37 km，灌区渠道布置见图2及相关参数见表1。

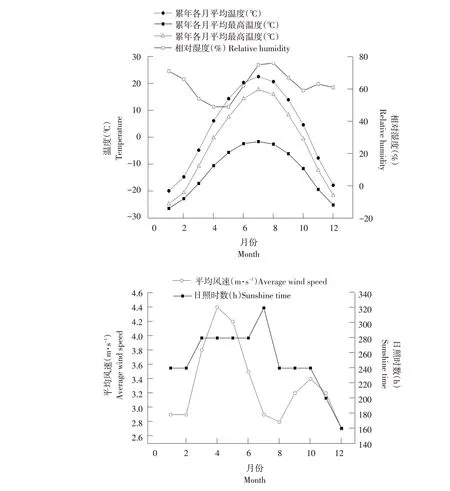
图1 灌区气象因子年内变化Fig.1 Annual changes of meteorological factors in irrigated areas

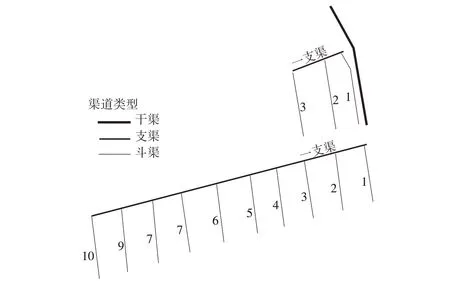
图2 灌区渠系布置Fig.2 Schematic of canal system arrangement in irrigation area

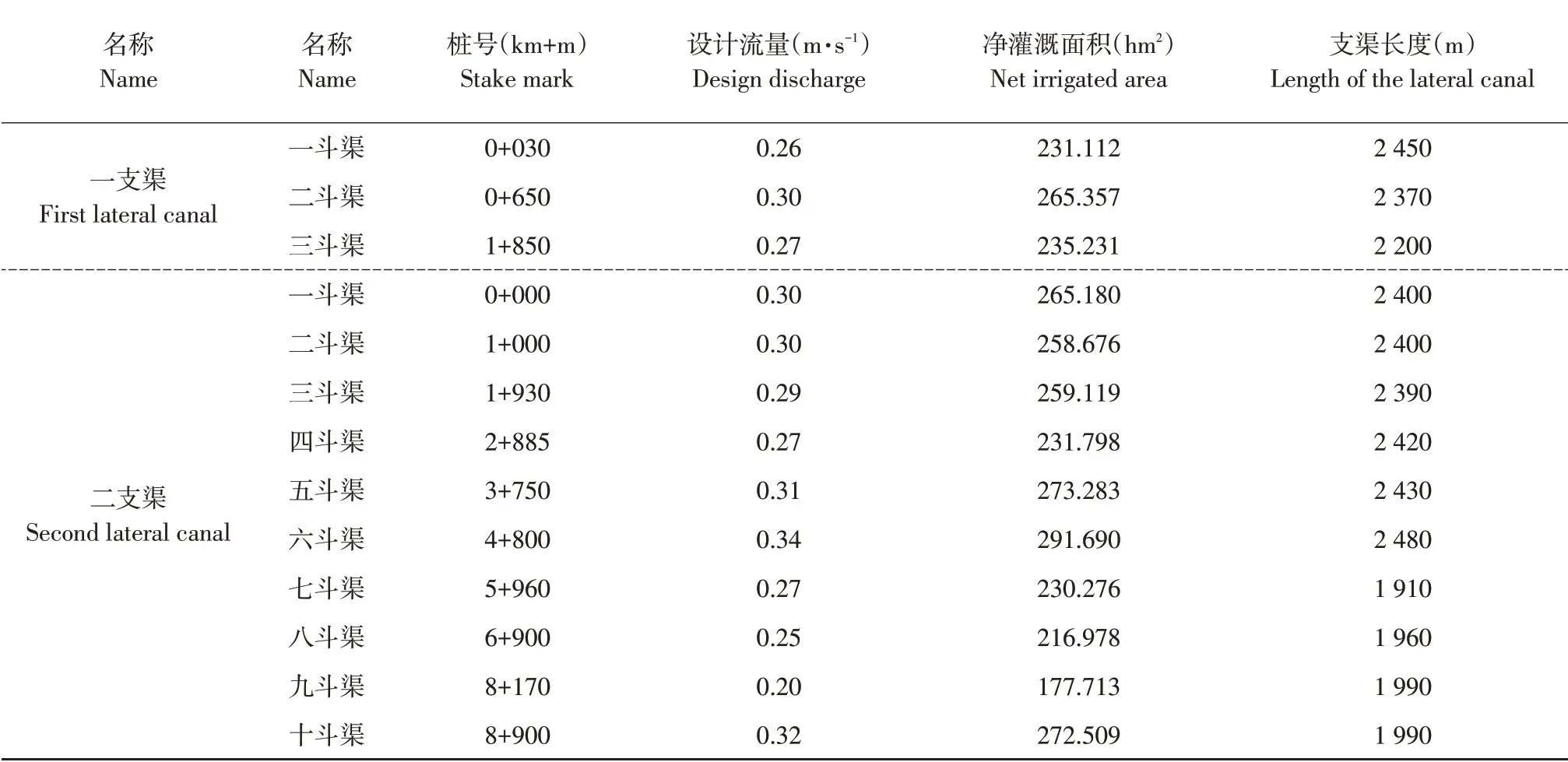
表1 各级渠道相关参数Table 1 Relevant parameters of channels at all levels

根据富裕灌区多年降雨资料分析，与设计保证率p=75%接近年份有1978 年、1996 年和1967年，分析这3 年水稻灌溉制度：1978 年泡田期降雨较少，所需灌水量较大，生育期降雨分布不均匀，拔节孕穗和抽穗开花期等关键生育期降雨少，不利灌水，因此选定1978 年为典型年，以1978年灌溉制度作为设计灌溉制度。灌区灌溉面积33.684 hm2，作物在移植返青、分蘖、拔节孕穗及抽穗开花4个阶段总需水量为2 179 万m3，灌区可供水量为3 035 万m3，各生育阶段灌水天数及灌水次数见表2，将以上数据代入模型，采用上述NSGA-Ⅱ模型求解。

表2 作物各生育期灌水参数Table 2 Irrigation parameters of crops at different growth stages

2.2 数据分析

根据上述所构建模型，采用NSGA-Ⅱ求解，算法选择群体规模为200，迭代次数设置为100，为保证子代种群每个个体充分交叉，交叉概率采用0.8。由于该算法可产生多组非劣解，综合考虑灌区供水情况及灌区效益，抽取地下水灌溉将产生电费消耗，故选择灌区地下供水量较小一组解作为灌区灌水方案。结果见图3～6。

各生育阶段一支渠及二支渠配水开始时间与配水结束时间见图3，而干渠配水开始时间与配水结束时间则为下级渠道配水开始时间最小值与结束配水时间最大值。由图3可见，一支渠在移植返青、分蘖、拔节孕穗、抽穗开花等阶段配水时间分别为2～11、9～31、2～15、6～18 d，而二支渠在各阶段配水时间则为1～12、9～35、2～18 及3～18 d，则干渠在各生育阶段配水时间为1～12、9～35、2～18 及3～18 d，与优化前相比均减少，表明各级渠道输水平均流量增加，减小渠道输水损失。

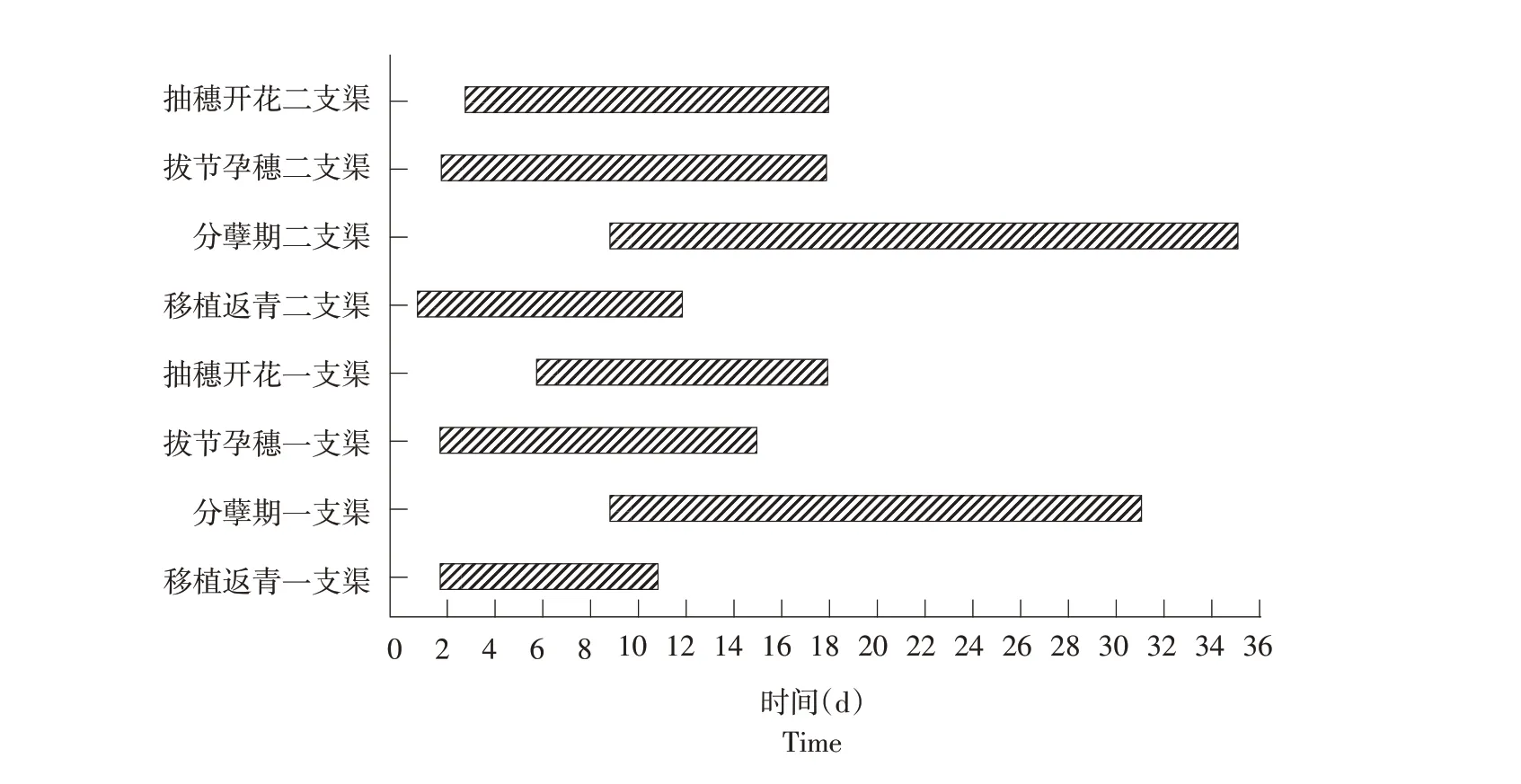
图3 各时期渠道配水过程Fig.3 Water distribution process of channel in each period

将各支渠道优化后配水流量及流速绘制成图4、5。可见，优化后各渠道流量及流速在各生育阶段变化平稳，未出现剧烈波动情况，各渠道流速均满足渠道设计不淤流速及不冲流速要求，符合渠道实际运行过程中流速限制。对比优化后配水流量与渠道设计流量，一支渠各阶段配水流量变化在其设计流量0.83 m3·s-1±9%范围内变化，说明优化后一支渠可达到渠道最佳运行状态；遗传算法根据达尔文生物进化论作优胜劣汰处理，灌区二支渠控制灌溉面积大，需输送水量大，而一支渠所控制灌溉面积小，在作物生育阶段输送水量少，二支渠为满足目标函数二要求，使二支渠配水流量减少而配水时间延长，证明遗传算法优越性。

灌区流量-开度计算是实现灌区水量调度自动化关键，富裕灌区渠系闸门均为平板单孔闸门且闸孔自由出流，根据优化求解得到各渠道配水流量作相关计算，得到渠道各生育阶段水深及各闸门开度绘制图6。可见，各渠道在满足渠道过流能力要求下闸门开度均小于渠道水深，根据渠道流量变化，在灌区实际运行中各分水口水位保持稳定，可保证下级渠道取得规定流量。

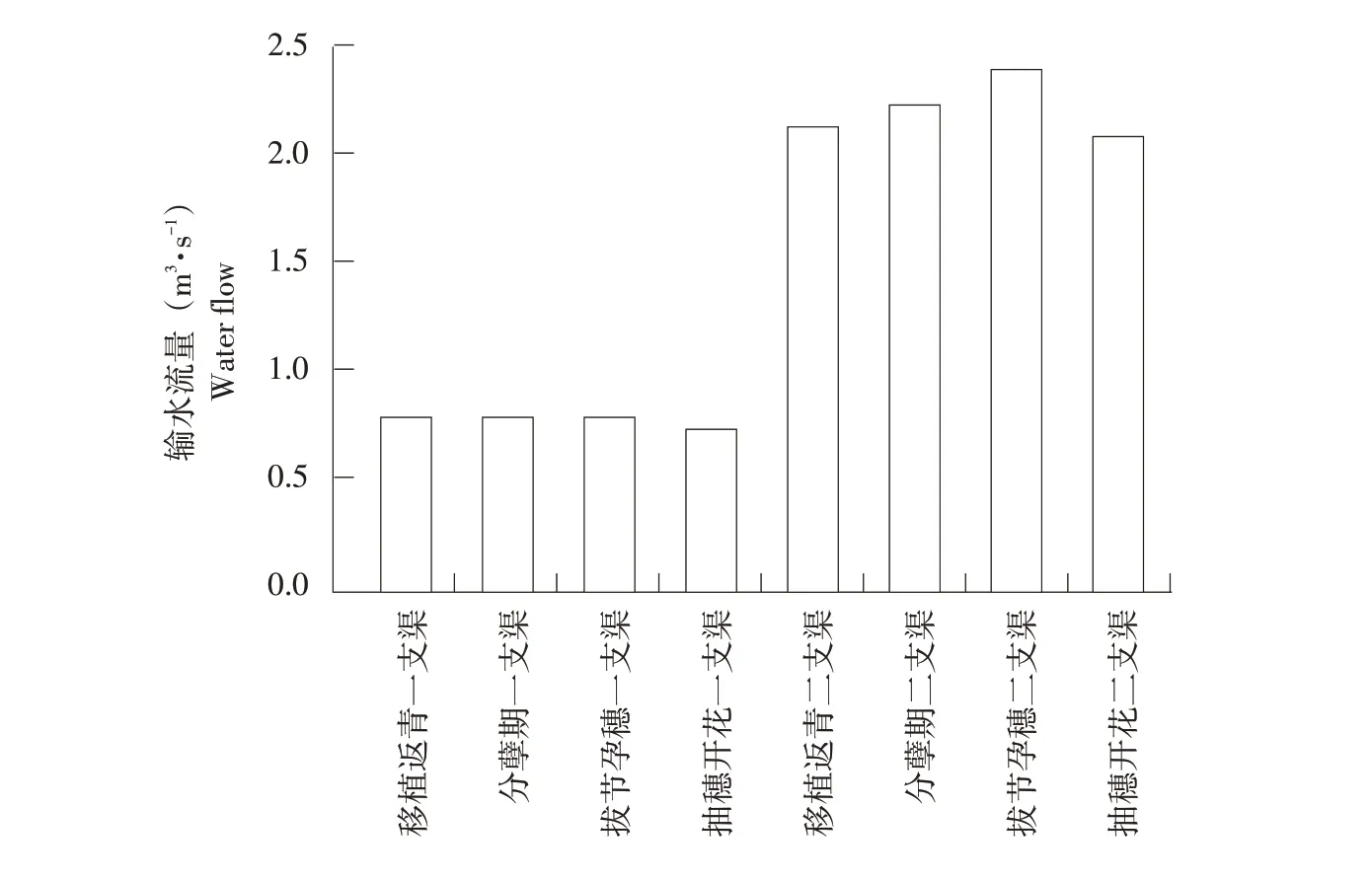
图4 各时期渠道配水流量Fig.4 Flow of channel distribution in each period

图5 各时期渠道配水流速Fig.5 Flow rate chart of channel distribution in each period

图6 各时期渠道水深闸门开启高度Fig.6 Opening height chart of channel water depth gate at different periods

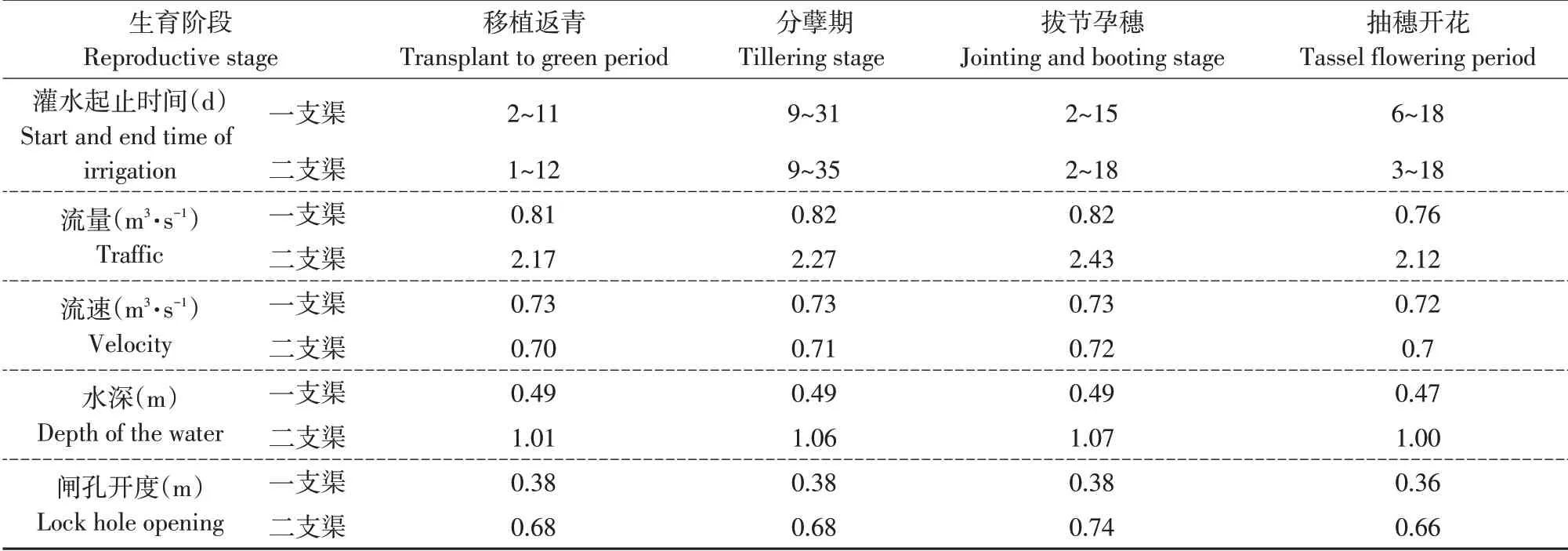
表3 灌区优化结果汇总Table 3 Summary table of irrigation optimization results

3 结论

本文以黑龙江省富裕灌区为例，充分考虑渠道输水过程中流量及时间不确定性特点，建立多目标灌区骨干渠道优化配水调度模型，运用多约束带精英策略非支配排序遗传算法求解。比较优化后求解结果与灌区传统配水方案可见，上级渠道各生育阶段配水时间与灌区管理部门人工制定配水计划规定时间相比均减小，缩短灌区渠系引水持续时间，在配水过程中配水流量变化较均匀，渠道流速也在渠道要求不淤流速及不冲流速范围内，根据优化结果求解闸门对应开启高度，可实现分水口水位、通过流量精确控制。表明运用本文模型和算法在满足灌区渠道实际运行水量及流量要求前提下确定灌区渠系配水方案，并以此方案为依据调节灌区渠系配水时间、配水流量及闸门开启高度，可提高灌区渠系配水精度，使配水过程更科学、合理、高效，满足灌区管理现代化要求。模型根据已有经验推求总结得到的经验公式，具有普遍适用性，可较好解决灌区渠系优化配水调度问题，为富裕灌区及类似灌区配水优化调度问题提供理论支持。