神经网络校正的EKF在水下被动目标跟踪中的应用研究
丁 一,张 瑶,李冠男
1(中国科学院 沈阳自动化研究所 机器人学国家重点实验室,沈阳 110016)
2(中国科学院 机器人与智能制造创新研究院,沈阳 110016)
3(中国科学院大学,北京 100049)
E-mail:dingyi@sia.cn
1 引 言
被动目标跟踪不会主动发出探测信号,而是被动地采集辐射噪声信号并解算出目标方位角信息,以此来进行目标跟踪,相对于主动目标跟踪隐蔽性好,在军事上有着广泛的应用.由于传感器不能获得距离的量测信息,只有一维的角度信息,因此被动目标跟踪是一种不完全的观测.同时由于其观测方程为非线性,对目标的观测又属于非线性观测,因此常规的线性滤波方法难以得到较高的估计精度[1].
在被动目标跟踪领域具有十分广泛应用的是扩展卡尔曼滤波(EKF),EKF可以将卡尔曼滤波应用在弱非线性模型上,通过线性化技巧,将其转化为一个近似的线性滤波问题.EKF在系统非线性程度不高且测量误差不大的情况下,其性能比较可靠,但在实际的水下被动目标跟踪中,EKF很容易出现滤波误差变大与发散的情况,主要原因有:
1)量测方程是强非线性的,线性化方法产生的误差较大.
2)系统状态信息是四维的,而量测信息是一维的,估计起来困难较大.
3)目标机动时,系统运动模型与噪声模型失配等.
针对水下被动目标跟踪应用滤波时效果不够理想的问题,国内外也有相关的研究[2-4].考虑到BP神经网络具有实现任何非线性映射的能力,本文将BP神经网络算法引入到被动目标跟踪滤波中,提出一种由BP神经网络自适应校正扩展卡尔曼滤波中滤波误差的方法.利用BP神经网络可实现任何非线性映射的能力,构建出卡尔曼滤波状态方程中输入变量和输出变量的关系[5],预测出在一定条件下的滤波误差的分布规律[6],再将学习过的误差反馈到滤波器末端,实现对EKF滤波误差的校正,从而提高了目标跟踪滤波精度[7-10].最后,通过仿真和真实试验验证了该方法的有效性.本文提出的方法与传统EKF方法相比,在跟踪精度、稳定性等方面都有了很大的提升.
2 问题描述
航行器与目标均工作在浅水区域时,通常可忽略目标深度信息,目标运动模型抽象为二维平面.目标始终作匀速直线运动,而观测站为确保可观测性采用了一定的机动策略,目标和观测站的相对运动态势如图1所示.
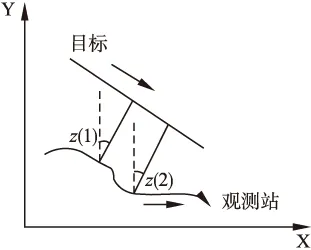
图1 目标和观测站的相对运动态势图
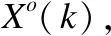
目标的状态方程和量测方程可以表示为如下形式[8]:
X(k)=AX(k-1)+w(k)
(1)
(2)

由式(1)和式(2)可知,目标的状态方程是线性的,而其量测方程含有复杂的非线性函数arctan(·),所以,在使用线性化滤波算法时需要首先对其进行线性化变换.
3 基于BP神经网络校正的卡尔曼滤波方法
3.1 扩展卡尔曼滤波
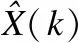
扩展卡尔曼滤波算法的基本公式如下[1]:
状态一步预测:
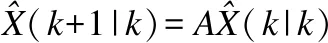
(3)
协方差矩阵一步预测:
P(k+1|k)=AP(k|k)AT+Q
(4)
滤波增益:
K(k+1)=P(k+1|k)HT[HP(k+1|k)HT+R]-1
(5)
协方差矩阵更新:
P(k+1|k+1)=[I-K(k+1)H]P(k+1|k)
(6)
状态更新:
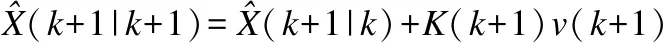
(7)
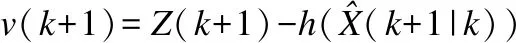
(8)
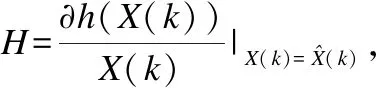
扩展卡尔曼滤波的五个基本方程将卡尔曼滤波分为两个过程,一个是时间更新过程,式(3)(4)进行一步预测更新,将时间从k递推更新到k+1,其余式子计算对时间更新值的修正量,该修正量由时间更新的质量优劣P(k+1|k)、观测信息的质量优劣R、观测与状态的关系H以及具体的观测信息Z(k)所决定,该修正量校准了时间更新值,得到一个更为精确的滤波估计值,这一过程描述的是滤波的估计过程.
3.2 神经网络辅助校正卡尔曼滤波过程
由于BP神经网络对非线性系统强大的学习能力[7],我们以减小卡尔曼滤波误差为目标,将卡尔曼滤波的估计能力和神经网络的学习能力相结合,采用神经网络来辅助校正卡尔曼滤波过程,从而抑制滤波器的发散.
通过(7)式可知,卡尔曼滤波的状态更新由以下三部分所构成[10]:
②卡尔曼增益:K(k+1)
③新息:v(k+1)
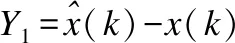
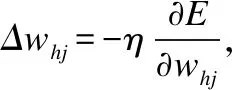
本文中的神经网络结构如图2所示.
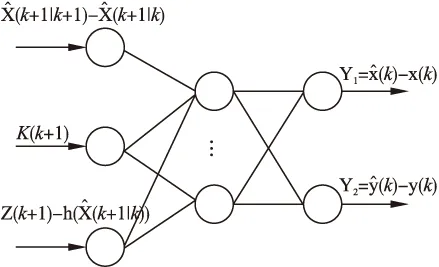
图2 BP神经网络结构
具体步骤如下:
1)首先要确定神经网络的结构,包括隐层的个数,隐层的结点数.
2)在网络中输入大量足够精度的训练样本数据,根据误差逆传播算法进行神经网络的离线训练,得到神经网络的权值阈值参数.
3)将滤波过程和神经网络同时在线运行,滤波输出估计值结果,神经网络预测出滤波估计误差.
4)将得到的状态估计值与神经网络预测的估计值误差进行融合处理,得到一个修正之后更为精确的状态估计值.
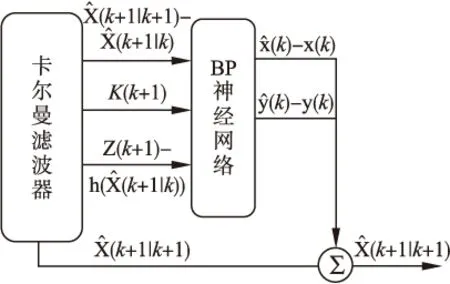
图3 神经网络辅助卡尔滤波器结构图
卡尔曼滤波中间变量与滤波误差之间存在很大的相关性,这种关系虽然无法准确的通过数学模型来表示,但是可以通过该BP神经网络来对这种非线性关系进行拟合[11-13],描述出卡尔曼滤波状态更新方程输入与输出之间的非线性关系,将神经网络预测得到的滤波误差值信息输送给滤波估计值,从而实现了对滤波结果的修正,提高了滤波的相对精度,该方法的原理框图如图3所示.
4 仿真分析
4.1 仿真参数设置
仿真按照上文问题描述中的目标与观测站的相对运动态势构建二维平面坐标系,跟踪过程中目标通过改变航向与航速进行机动.通过MATLAB软件编程完成实现了传统的扩展卡尔曼滤波方法和神经网络辅助校正卡尔曼滤波方法的仿真对比[14].
首先需确定神经网络的隐含层层数以及结点数,一般来说,隐层的数量越多,对系统的非线性映射能力即越强,但过高会导致网络的学习计算量爆炸,学习速度变慢以及过拟合等情况.
综合考虑计算时间与精度,在仿真中选取的神经网络层数结构为4层,输入层结点数为9,第一层隐含层结点数为10,第二层隐含层结点数为12,输出层结点数为2.隐含层的激活函数皆为tansig,是一种sigmoid的函数,输出限制在[-1,+1]之间,该函数精度比线性函数要高得多,但计算量较大.输出层的激活函数为purelin,是一个线性函数,可以对神经网络的输出结果进行更为精确的映射.
由于激活函数的值域是有限制的,且各个输入变量的数据范围不一致,数据范围大的对神经网络训练产生的作用可能会偏大,而数据范围小的作用就可能会偏小,因此需要将输入数据进行归一化操作,输出预测值再进行反归一化.
训练函数使用动量及自适应lr的梯度下降法,网络连接权值参数初值随机产生,网络学习率η取值0.3,最大迭代次数epoch为1200,网络输出的均方误差达到0.001时则停止训练.
4.2 仿真结果分析
本文采用离线训练的方式.在滤波结束后,输入一条经滤波器估计完成的目标轨迹,采用随机抽取的方式将轨迹上的数据点作为训练集和测试集,将训练集输入给神经网络进行学习.为了验证神经网络对卡尔曼滤波过程的校正效果,采用了数值仿真试验和外场海试试验数据进行算法验证.
对单目标进行仿真分析,初始位置坐标为(0,1400),x轴和y轴对应的速度为2m/s和10m/s,高度保持不变,将真实轨迹加入一定的高斯白噪声.
传统的EKF方法得到的估计的轨迹如图4(a),可以看到,当目标发生机动转弯时,滤波跟踪精度严重下降,最大误差在200m左右.而采用神经网络辅助卡尔曼滤波修正后的目标轨迹如图4(b),与图4(a)相比较,可以观察到本文方法有效地校正了机动转弯后跟踪效果差的点,该方法得到的估计轨迹始终保持在真实轨迹附近.神经网络预测的x轴滤波误差和y轴滤波误差如图5(a)(b),从图中可以看出经过了大量数据的学习,预测的滤波误差趋势与真实值大致相同,但由于输入的训练数据数量较少,且数据本身存在一定的随机性,在预测过程中出现了跳变点.

图4 单目标仿真结果对比
图5 神经网络预测滤波误差效果图
在单目标仿真试验进行良好的基础上加入一条轨迹,对多目标进行仿真实验.目标1的初始位置为(1400,50),速度为(-6,0),目标2的初始位置为(0,1400),速度为(2,-6),跟踪过程中两个目标交叉.图6(a)(b)对比可以看出,在EKF估计的滤波结果有发散的趋势时,经过BP神经网络校正过的轨迹始终围绕在真实值附近.
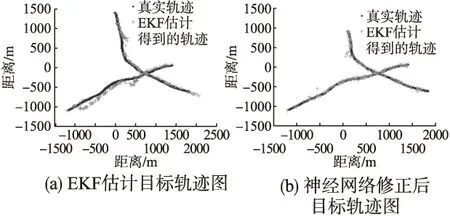
图6 多目标仿真结果对比
经实验得出,单目标校正前RMSE=381.3m,校正后RMSE=73.6m,多目标校正前RMSE=135.17m,校正后RMSE=31.64m.
采用真实海试试验数据,实际场景中无法达到仿真中传感器检测概率为1,且无杂波的理想环境,因此为了保证对目标的可观测性,设定载体的路线为往返运动,而目标始终静止在原点处.观测站载体的初始位置为北纬29.56°东经118.96°,初始航向角198.33°、俯仰角0°、横滚角0°,量测噪声的方差R设置为3°,被动声纳接收到的目标角度值为图7,可以看出测量数据断续,且有杂波污染.
将各个相对位置统一到北东地(NED)坐标系下,训练完成后,抽取大量测试集对比纯滤波结果和神经网络校正滤波结果,如图8所示,可以看出误差有大幅度的降低,统计均方根误差后发现,RMSE由956.24m减小至182.51m.因此,在实际水下环境中,该算法也通过了验证.
从数值仿真实验的结果可以看出,该算法可以应用在单目标情况下,也可以应用在多目标情况下,EKF-BP算法的精度远远高于EKF算法.外场数据的实验结果则说明了,EKF在有杂波干扰且量测断续的情况下,收敛速度很慢,而本文提出的算法误差大大减小,校正后被动目标跟踪过程的精度和稳定性都有了明显的提高.在实际海试试验中,由于没有对传感器的数据进行关联筛选,因此校正后的结果虽然比之前的相比有所改进,但仍有很多离散的大误差点,后期将对传感器获得的量测角度加入数据关联环节,以提高滤波精度.
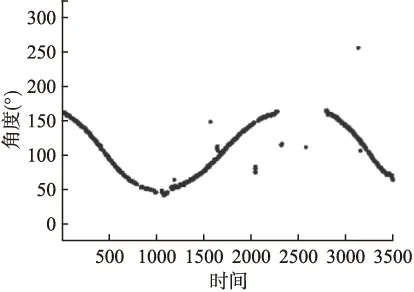
图7 被动声纳接收到的角度量测值
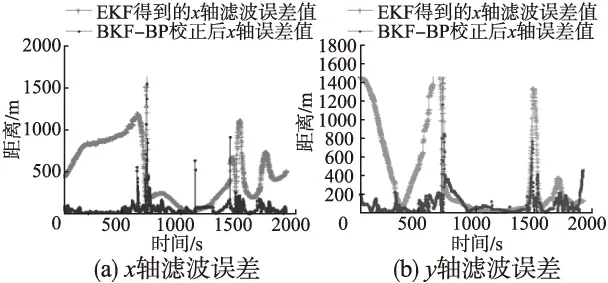
图8 校正前后的滤波误差对比图
5 总 结
本文针对扩展卡尔曼滤波应用于水下被动目标跟踪易于发散的问题,提出将神经网络与扩展卡尔曼滤波相结合的方法.经过理论分析和仿真验证发现:经过神经网络校正后的卡尔曼滤波过程,可以抑制目标载体机动以及强非线性模型等带来的不良影响,通过神经网络对卡尔曼滤波状态方程输入到输出变量映射关系的构建,在一定程度上减小了滤波估计误差,提高了滤波误差的精度,进而提升了水下被动目标跟踪的可靠性与鲁棒性.
但神经网络与卡尔曼滤波相结合的技术方法,仍存在需要完善的细节.比如神经网络的结构层数以及初始权值等参数是否能有一种更高效率的方法来确定,目前多是根据经验进行选取,导致训练时效率较低等问题.后续需要进一步深入进行研究和探讨,从而得到更精准的目标跟踪结果.

