利用时空轨迹数据的城市可达区域计算方法
柴明璐,唐晓岚,陈潇然,陈文龙
(首都师范大学 信息工程学院,北京 100048)
E-mail:tangxl@cnu.edu.cn
1 引 言
随着现代城市规模的快速扩张和汽车数量的飙升,城市交通系统日趋复杂,带来了愈加严峻的交通问题,严重影响了城市通勤效率和降低了市民在日常生活中的出行质量.为了引导驾驶行为,城市中可达区域的计算旨在得到车辆或乘客在起始时间由起始位置出发通过特定的查询时间段可以抵达的有界区域.
如图1所示,可达区域在各式各样的城市应用中起着重要的作用.其中,图1(a)所示的基于兴趣点(POIs)的推荐中,低电量电动汽车想找寻附近能够在剩余电量的行驶时间内抵达到的充电站时,那么位于可达区域内充电站将会被推荐给驾驶员.图1(b)所示的基于空间距离的服务覆盖分析.计算外卖配送员在特定时间段内的可达区域,以便准时将餐食配送到位,因此,餐厅可以依据可达区域对配送员及车辆资源的分配进行相应的调整.
由于城市中交通情况每时每刻都发生着变化,因此可达区域随着不同的起始时间也是不同的.如图1(a)中的虚线圈和实线圈分别表示上午8:00和下午4:00的可达区域.
显然,上午8:00时区域内有2个充电站被推荐给驾驶员,而下午4:00时则有6个充电站满足条件被推荐给驾驶员.同样,在图1(b)中,餐厅在下午7:00仅能为可达区域内的2个客户提供服务,而在中午12:00则能为可达区域内的4个客户提供服务.
现有的研究工作中主要通过分析静态的道路网络在空间可达性上支持上述城市应用.例如,判定起点位置和终点位置间是否存在最短距离(欧式距离,曼哈顿距离等)的连接路段集.由于没有考虑到城市中复杂的交通情况和可达区域随时间变化的问题,这类基于道路网络的方法缺乏对时间因素的深入讨论.

图1 城市应用示例
如今,我们通过配备在车辆上的车载定位装置(如北斗,GPS)能够方便地获取大量的轨迹数据,这些富含城市时空信息的轨迹数据为可达区域的挖掘提供了新的可能性.综上所述,如何通过整合城市交通数据从中提取出空间和时间的特征来计算准确的可达区域是一个关键问题.
本文提出了一种利用大型城市出租车GPS轨迹数据挖掘的时空可达区域计算方法(RAC),由3个主要计算过程组成:1)可达点计算:根据查询时间和空间约束以及查询时间段对轨迹数据进行过滤和提取得到目标轨迹,接着通过合并目标轨迹的轨迹点来计算唯一对应的可达点,以降低后续步骤的计算复杂度;2)覆盖路段计算:通过将可达点映射到城市道路得到覆盖路段,然后聚合同一覆盖路段上符合距离约束的可达点,在降低可达点集冗余性的同时简化了可达区域边界的计算过程;3)边界路段计算:通过依次选取最大轨迹抵达数的覆盖路段作为边界路段来保证可达区域的边界在各个方向上都具有最大机会抵达的特性.
本文的主要贡献总结如下:1)提出了一种新型的可达区域的计算方法(RAC),通过挖掘大量城市交通数据为城市应用提供了一种可行的数据驱动解决方法;2)为了有效地找到可到达区域的边界,RAC引入了可达点的计算,过滤不在查询时间段内的轨迹数据,找到由一系列轨迹点组成的目标轨迹,接着计算得到唯一的可达点,从而极大程度上降低了覆盖路段计算方法的复杂度;3)为了找到可达区域在各个方向上的最大机会抵达的边界,设计了一种基于最大轨迹抵达数的边界路段选择策略;4)为了评估RAC的性能,本文采用来自北京34040辆出租车1个月的真实轨迹数据进行实验.实验结果表明,RAC的可达区域面积仅是传统方法的20%和30%;且在不同的起始位置实验中,RAC的轨迹覆盖率达到74%左右;而在算法运行效率实验中,RAC在不同规模的数据集中始终保持着最高的运行效率.因此,本文提出的RAC与其他方法相比能够得到更准确的可达区域和保持较高的轨迹覆盖率.综上,RAC在计算效果和算法运行效率上是可行的.
本文的结构组织如下:第2节介绍相关工作;第3节介绍算法的基本概念与符号及算法设计;第4节详细讨论RAC的3个主要计算过程;第5节介绍基于车辆轨迹数据的实验结果及分析;第6节总结全文.
2 相关工作
本节将讨论3个与城市可达区域紧密相关的研究主题,包括城市计算、轨迹查询和可达性查询.
城市计算作为一个新兴的研究课题,集成了城市传感、数据管理、数据分析和城市服务.通过挖掘城市中每时每刻产生的数据来解决如交通拥堵、能源消耗和环境污染等各式各样的问题[1,2].文献[3]提出了一种基于地理相似区域查询技术,通过分析兴趣点(POIs)数据在城市中找出与给定区域Top-k相似的区域.文献[4]提出了一种DRoF(Discovering Regions of different Functions)框架通过挖掘人类移动轨迹数据同时结合域内的兴趣点(POIs)数据的匹配来区分城市中的不同功能区域.文献[5]通过提取车辆GPS轨迹数据的集群来在地图上建立人类移动目的地,进一步匹配已有的行政边界数据来找寻人类可以抵达的边界.上述在城市计算中各个方向的研究方法为基于轨迹数据的城市可达性查询提供了研究思路.
轨迹查询旨在通过对具有丰富时间空间信息的轨迹数据进行查询为目前城市智能交通服务提供技术支持,其包含诸如范围查询和路径规划等热门的研究课题[6-9].在范围查询研究中,基于轨迹数据在给定区域内查询移动对象在某个时间段内移动到各个路段的概率,通过对路段概率的统计进行路段的选择.文献[10]通过对轨迹数据库内每个移动对象建立有效的索引来加速给定区域内的移动物体将朝向下一个位置移动的概率计算.文献[11]则是通过对大规模轨迹数据挖掘获得给定区域中最具影响力的k个位置,以此为诸如广告牌位置选址等应用提供有效的建议.此外,路径规划广泛地研究了在当前城市路网中任何路段皆可达时,从一个位置到另一个位置间的路径如何进行规划的问题.其中Dijkstra算法及相关改进方案很好地解决了在城市路网中最短路径查询的问题[12-15].文献[16]提出了一种估计路段行驶时间的模型PTTE(Path Travel Time Estimation),通过细化挖掘最近轨迹数据和历史轨迹数据来达到实时评估城市路网中任何路段上的行驶时间的目的.文献[17]通过基于大规模历史轨迹数据的路径预测找到特定时间段内车辆行驶最频繁的路段.与上述轨迹查询研究不同,本文的目标是通过轨迹数据挖掘在城市中从起始位置和开始时间计算出在给定时间间隔内具有时空特征的可达区域.
与轨迹查询不同的是,可达性查询通常基于静态图论分析城市道路网络中是否存在从一个位置到另一个位置的合适的路径,以此来量化位置间可达性[18-21].文献[22]提出了一种查询方法OMP(Optimal Meeting Point Query)来寻找给定欧几里德空间内的道路网络中的最佳相遇位置.另一些可达性研究集中在城市路网数据中的最近邻查询(Nearest Neighbor Query).其原理是基于空间最短距离在给定查询区域内的路网找出给定位置的k个最近邻居(路段上位置或路段)[23,24],以此来评估给定位置和这些邻居节点的可达性.然而,基于静态图论分析得出的可达性查询结果仅表示空间关系,而城市交通状况随时间变化很大,路段间的可达性随着时间的推移也会有很大的变化,显然在依赖查询时间的城市应用中,已有的研究无法提供有效的可达性判断.而车辆轨迹数据作为一种时空数据能够优化可达性查询.文献[25]提出一种新型的轨迹数据驱动的可达性查询方法,根据在道路网络上收集的大量城市轨迹数据找到可达的路段,但是无法提供从查询起始位置出发各个方向上都是最大机会抵达的路段.综上所述,本文提出的时空可达区域计算方法将动态的出租车GPS轨迹与静态的城市道路网络相关联,并通过基于最大轨迹抵达数的边界路段选择策略来保证可达区域的边界在各个方向上都是最大机会抵达,为城市应用提供具有时间和空间特征的可达区域计算方法.
3 算法概述
本节给出时空可达区域计算方法(RAC)的基本概念与符号以及算法设计,这些基本概念和符号的使用将在第4节进行具体的描述.
3.1 基本概念与符号
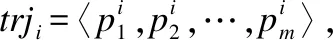
为了从Trj中得到用于计算可达区域的目标轨迹,本文引入了查询时空点和查询时间段对其约束.查询时空点指在计算时空可达区域时的起始位置和起始时间,在算法中的作用是对轨迹trji进行时间-空间复合约束,记为QP=(qlon,qlat,st),其中qlon和qlat分别是起始位置的经度和纬度,st是起始时间.查询时间段则是指自查询时空点QP出发计算时空可达区域的给定时间片段,依据自查询时空点开始行驶的时间基数eta和时间区间阈值εTT计算得到,记为T=[st+eta-εTT,st+eta+εTT].
当轨迹trji满足查询时空点QP的时间-空间复合约束条件且在查询时间段T内存在有序轨迹点集时,则将该有序轨迹点集组成的轨迹片段称为目标轨迹oti,且所有车辆轨迹中的目标轨迹集用OT={ot1,ot2,…,otl}表示.
本文以如图2示例来详细地描述从轨迹中提取目标轨迹的过程.令北京火车站为查询时空点QP=(116.4210°E,39.9035°N,8:00am),查询时间段为T=[8:18am,8:22am](εTT=2minutes),车辆V1、V2和V3产生的轨迹trj1、trj2和trj3用单实线表示,目标轨迹用双实线表示.其中,V1在8:00am-8:22am期间处于行驶状态,因此选择trj1中T区间内的轨迹作为目标轨迹(途径A和C间产生的轨迹).V2在8:05am到达D随即停止行驶,由于车辆配备的GPS设备通常定期产生轨迹数据,而不对车辆行驶状态进行检查,因此trj2在8:05am之后仍记录着D点位置作为轨迹数据.通常,现有的研究在进行轨迹查询或计算时往往考虑trj2,而trj2显然不适用于[8:18am,8:22am]可达区域的计算(trj2应当用于8:05am左右的可达区域计算).同样的,V2到达F后随即停止行驶,因此选择trj3在8:18am-8:20am期间的轨迹作为目标轨迹.

图2 目标轨迹示例
为进一步简化后续计算,本文引入可达点对目标轨迹进行聚合运算.可达点由特定位置的空间信息和经过该位置的目标轨迹数组成,记为rpi=(rloni,rlati,numi),其中rloni和rlati表示该位置的经度和纬度,numi表示抵达或经过该位置的目标轨迹数量,称为可达点轨迹数.由于可达点rpi是由oti计算得到,因此每条目标轨迹oti对应着一个可达点,故初始可达点集为RP={rp1,rp2,…,rpl}.
接下来,通过引入路段、覆盖路段及边界路段基本概念找出构成可达区域边界的路段.路段是指由起点和终点构成且不包含交叉路口的道路片段,记为rj=(oj,dj).路段的起点用oj=(olonj,olatj)表示,olonj和olatj分别是起点的经度和纬度.相似地,路段的终点用dj=(dlonj,dlatj)表示.为便于分析,在以QP为原点的基于地理信息的坐标系中,本文令路段两端点与查询时空点QP的连线与横轴方向的夹角较小者为起点,较大者为终点.全部路段集则记为R={r1,r2,…,rz}.
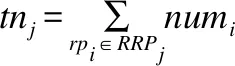
通过执行边界路段选择策略从覆盖路段集中选出的构成可达区域边界的覆盖路段称为边界路段,记为brj,边界路段集记为BR={br1,br2,…,bry}.边界路段选择策略使用覆盖路段的角度信息进行路段筛选,该角度信息包括覆盖路段crj的起点oj、终点dj以及可达点集RRPj和时空查询点QP连线与横轴正方向的角度,记为craj.计算方式如下:
对任意覆盖路段crj∈CR,计算起点oj和终点dj与时空查询点QP连线与横轴正方向的角度,分别记为oaj和daj,可达点集RRPj中的任意可达点rpτ和时空查询点QP连线与横轴正方向的角度记为rpaτ,可达点角度集记为RPAj={rpa1,…,rpaτ,…,rpaω},crj的覆盖路段角度记为craj={oaj,daj,RPAj}.所有覆盖路段的角度构成覆盖路段角度集,记为CRA={cra1,cra2,…,crax}.
本文中广泛使用的符号及术语由表1给出.
3.2 算法设计
本文提出的时空可达区域计算方法RAC由以下三个计算步骤构成.
表1 符号和术语
Table 1 Notations and terminologies

符号描 述Trj轨迹集,Trj = {trj1,trj2,…,trjn}QP时空查询点,QP=(qlon,qlat,st)T查询时间段,T=[st+eta-εTT,st+eta+εTT]OT目标轨迹集,OT={ot1,ot2,…,otl}RP可达点集, RP={rp1,rp2,…,rpl}R路段集,R={r1,r2,…,rz}CR覆盖路段集,CR={cr1,cr2,…,crx}BR边界路段集,BR={br1,br2,…,bry}CRA覆盖路段角度集,CRA={cra1,cra2,…,crax}εQT查询时空约束的时间阈值εQD查询时空约束的距离阈值εTT查询时间段T的时间阈值εDD可达点合并过程的距离阈值
1)可达点计算:首先在轨迹集Trj中找出满足查询时空点的时空约束且在查询时间段T的轨迹数据记为目标轨迹oti,进一步计算出目标轨迹集OT.然后通过合并oti∈OT的轨迹点来得到可达点rpi,进一步计算出可达点集RP.
2)覆盖路段计算:首先通过匹配可达点集RP与路段集R,得到覆盖路段集CR.为了简化下一步边界路段计算过程,需对覆盖路段crj上的可达点进行合并.具体地,若覆盖路段crj上存在距离小于等于给定距离阈值εDD的两个可达点时,则将这两个可达点合并成一个新的可达点.
3)边界路段计算:首先从覆盖路段集CR中选出轨迹抵达数最大的覆盖路段crm加入到边界路段集BR中.然后依据覆盖路段角度cram,更新其他覆盖路段crn及其角度值cran.
4 可达区域计算方法
4.1 可达点计算
(1)
其中,εQD是QP时空约束检查的距离阈值,εQT是QP时空约束检查的时间阈值.然后,从QP时空约束检查返回值为TRUE的轨迹trji中选出位于查询时间段T的序列点记为目标轨迹oti,若trji中不存在位于T的序列点则将trji抛弃.目标轨迹oti表示如下:
(2)
对每条目标轨迹oti计算得出可达点rpi,其中rpi的经度rlon由oti的序列点的平均经度计算得到,rpi的纬度rlat由oti的序列点的平均纬度计算得到.由于每条目标轨迹映射到唯一的可达点,因此可达点轨迹数numi为1,rpi的计算公式如下:
(3)
可达点计算过程由算法1给出.第1-2行初始化目标轨迹集OT与可达点集RP为空集.第3-8行遍历车辆轨迹trji∈Trj,判断trji经QP时空约束检查的返回值,若返回值为TRUE,则将trji在查询时间段内的轨迹记为目标轨迹oti,并加入目标轨迹集OT,反之则进行下一条轨迹判断.第9-13行遍历目标轨迹oti∈OT,计算可达点rpi的相应属性值.第14行终止算法并返回可达点集RP.
算法1.可达点计算算法
输入:1)Trj={trj1,trj2,…,trjn},
2)QP=(qlon,qlat,st),
3)T=[st+eta-εTT,st+eta+εTT].
输出:RP
1. initializeOT=∅;
2. initializeRP=∅;
3.foreachtrji∈Trjdo
4.iftheQPchecking fortrjireturns TRUEthen
5. select the part oftrjiduringTasoti;
6.OT←{oti}∪OT;
7.end
8.end
9.foreachoti∈OTdo
10. calculaterloni,rlatiandnumiofrpi;
11.rpi=(rloni,rlati,numi);
12.RP←{rpi}∪RP;
13.end
14.returnRP;
4.2 覆盖路段计算
算法1执行后得到初始可达点集RP,由于每条目标轨迹对应着一个可达点,庞大的输入轨迹数量导致可达点的数量庞大且位置分散,不利于时空可达区域的计算.因此,本方法引入覆盖路段来合并位于同一路段且距离近的可达点,以降低数据的冗余性,提高计算的效率和结果的精度.
算法2给出覆盖路段计算的伪代码.第1行初始化覆盖路段集CR为空集.第2-12行检查每条路段rj上是否存在可达点rpi,若存在,则rj是覆盖路段,将rj加入到CR中,同时更新RRPj和tnj的属性值,然后将rpi从RP中删除.第13-21行,当位于同一覆盖路段上的两个可达点间的距离小于等于预设距离时,将其合并为一个新的可达点.最后,第22行终止算法并返回覆盖路段集CR.
算法2.覆盖路段计算算法
输入:1)RP={rp1,rp2,…,rpl},
2)R={r1,r2,…,rz}.
输出:CR
1. initializeCR=∅;
2.foreachrj∈Rdo
3.ifRP= ∅then
4. break;
5.end
6.if∃rpi∈RPwhich is onrjthen
7.CR←{rj}∪CR;
8.RRPj←{rpi}∪RRPj;
9.tnj=numi+tnj;
10.RP←RP-rpi;
11.end
12.end
13.foreachcrj∈CRdo
14.forany two reachable pointsrpα,rpβ∈RRPjdo
15.ifdis(rpα,rpβ)≤εDDthen
16. mergerpαandrpβintorpnew;
17.RRPj←RRPj-rpα-rpβ;
18.RRPj←{rpnew}∪RRPj;
19.end
20.end
21.end
22.returnCR
在可达点合并过程中,计算位于同一覆盖路段crj上的可达点rpα和rpβ的距离dis(rpα,rpβ),并检查是否满足下式约束.
dis(rpα,rpβ)≤εDD
(4)
其中,εDD是给定合并过程的距离阈值.若满足约束,则合并后的可达点rpnew通过下式计算得出:
(5)
显然,新得到的可达点rpnew位于可达点rpα和rpβ之间,且抵达rpnew空间位置的轨迹数是可达点rpα和rpβ的轨迹数的总和.
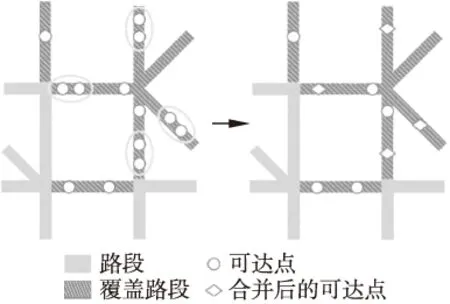
图3 可达点的路段匹配和合并示例
图3简要地描述可达点的路段匹配和合并过程,其中实线是不存在可达点的路段,阴影线是覆盖路段,圆形是合并前的可达点,椭圆内的可达点之间的距离小于等于距离阈值.合并后的可达点用菱形表示,可达点合并后的效果如图4中右图所示.
4.3 边界路段计算
在本文构建的以查询时空点QP为原点的基于地理信息的坐标系中,在同一方向上通常存在多条覆盖路段.如何选择最大机会抵达的覆盖路段作为边界路段是提高时空可达区域准确性的关键问题.因此,本文设计了一种基于最大轨迹抵达数的边界路段选择策略,目的是从覆盖路段集CR中选出构成时空可达区域的边界路段集BR,提高计算结果的精度.
边界路段计算过程由算法3给出.第1行初始化边界路段集BR为空集.第2-4行从CR中选择轨迹抵达数最大的crm加入到BR中.第5-7行遍历覆盖路段角度集CRA,当路段角度cran被cram包含时删除路段crn,否则执行第8-22行更新crn的属性值.待crn更新结束后执行23行删除路段crm.第25行终止算法并返回边界路段集BR.
算法3.边界路段计算算法
输入:1)CR={cr1,cr2,…,crx},
2)CRA={cra1,cra2,…,crax}.
输出:BR
1. initializeBR=∅;
2.whileCR≠∅do
3. selectcrm∈CRwith the maximumtnm
4.BR←{crm}∪BR;
5.foreachcran∈CRAdo
6.ifdam 7.CR←CR-crn; 8.else 9.foreachrpar∈RPAndo 10.ifoam 11.RPAn←RPAn-rpar; 12.RRPn←RRPn-rpr; 13.elseifoan 14. CASE 1; 15.elseifoam 16. CAES 2; 17.elseifoan 18. CASE 3; 19.end 20.end 21.end 22.end 23.CR←CR-crm; 24.end 25.returnBR; 具体地,基于最大轨迹抵达数的边界路段选择策略由两个阶段组成: 第1阶段,从CR中选出轨迹抵达数最大的覆盖路段crm,加入边界路段集BR中. 第2阶段,遍历覆盖路段角度集CRA,当任意覆盖路段crn的路段角度cran与选定的覆盖路段crm的路段角度cram存在以下角度关系时: oam (6) 此时cran被cram全包含,则将crn从CR中删除.反之更新crn的属性值,将满足dam 情况1(CASE 1).存在以下路段角度关系时: oan (7) 此时依据路段角度cran,将crn拆分成角度范围[oan,oam)的子路段crα=(oα,dα,RRPα,tnα)和角度范围(dam,dan]的子路段crβ=(oβ,dβ,RRPβ,tnβ).对任意可达点rpr∈RRPn,当rpar 情况2(CASE 2).存在以下角度关系时: oam (8) 此时对crn进行更新操作,从RPAn选取最小值rpas,将rps的空间属性值赋予dn,依据RRPn计算轨迹抵达数tnn. 情况3(CASE 3).存在以下角度关系时: oan (9) 此时对crn进行更新操作,从RPAn选取最大值rpae,将rpe的空间属性值赋予on,依据RRPn计算轨迹抵达数tnn. 对crn更新结束后,则将crm从CR中删除.判断CR是否为空集,若为空,结束遍历,否则继续执行策略. 算法1首先遍历轨迹trji∈Trj中的轨迹点,检查是否满足QP时空约束以及是否存在时间戳在查询时间段内的序列点集.由于不同轨迹的轨迹点数量不同,以|trji|max表示轨迹点数量的最大值,从轨迹集Trj计算目标轨迹集OT过程的时间复杂度为O(|Trj|×|trji|max).接下来,为每条目标轨迹oti∈OT计算可达点,得到可达点集RP,时间复杂度为O(|OT|).由于|OT|≪|Trj|×|trji|max,因此算法1最终的时间复杂度为O(|Trj|×|trji|max). 算法2首先遍历路段集R与可达点集RP,以时间复杂度O(|R|×|RP|)从路段集R中筛选覆盖路段集CR.接着在每条覆盖路段crj∈CR中,检查可达点集RRPj,将距离相近的可达点进行合并,以|RRPj|max表示一条覆盖路段上可达点数的最大值,该过程的时间复杂度为O(|CR|×|RRPj|max).由于|CR|≪|R|,|RRPj|max≪|RP|,因此算法2最终的时间复杂度为O(|R|×|RP|). 算法3的第1阶段以时间复杂度O(|CR|)从覆盖路段集CR中选出轨迹抵达数最大的覆盖路段crm.,第2阶段以时间复杂度O(|CRA|)从覆盖路段角度集CRA中筛选出与crm存在如式(6)角度关系的覆盖路段crn,并以时间复杂度为O(|RPAn|)更新crn的属性值.由于算法2合并可达点过程大大降低了crn的可达点集RRPn中的节点数,RPAn中的角度数也相应降低,故|RPAn|≪|CRA|,因此算法3最终的时间复杂度为O(|CR|×|CRA|). 为了评估本文提出的城市可达区域计算方法RAC的性能,利用北京市出租车轨迹数据开展了广泛的实验.原始的出租车轨迹数据收集于2015年6月份且行驶区域集中在北京市6环路以内的34,040辆出租车,总计有397,423,783条记录,具体的数据格式由表2给出.该数据集尚未公开. 表2 数据集的格式 Table 2 Format of dataset 字段格 式车辆ID5位数字: ddddd时间戳yyyy-mm-dd-hh-mm-ss; year-month-day-hour-minute-secondGPS纬度ddd.dddd;度GPS经度ddd.dddd;度速度ddd;厘米/秒 为了提高计算的准确性和执行效率,本文首先对原始轨迹数据进行预处理操作.具体地,本文清理了冗余的和无效的轨迹数据(速度为0),并提取了纬度在39.6578°N和40.1928°N,经度在116.0052°E和116.7357°E之间的数据构成了轨迹数据集Trj.同时,本文从OpenStreetMap[27]提取了2000多条道路数据构成路段集R,详细的实验配置如表3所示. 表3 参数设置 Table 3 Experiment configurations 参数值起始位置北京火车站:(116.4210°E,39.9035°N)王府井:(116.4052°E,39.9066°N)天通苑:(116.4062°E,40.0694°N)中关村:(116.3105°E,39.9817°N)起始时间{00:05,01:05,…,23:05}基础行驶时间30分钟查询时间段{[00:30,00:40],[01:30,01:40],…,[23:30,23:40]}查询时空约束的时间阈值30秒查询时空约束的距离阈值100米查询时间段T的时间阈值5分钟可达点合并过程的距离阈值500米 为了验证本文提出的可达区域计算方法的适用性,本文选出了5个不同的起始位置,其中以王府井为起始位置的实验将在5.1节详细讨论,其他起始位置点的实验将在5.2节讨论. 本文选择了经典的凸包算法GRAHAM[28]和最远距离优先的ANGLE算法作为对比算法.GRAHAM算法在基于地理的坐标系中绘制数据集的凸包来构成可达区域,凸包内所有的可达点将会被覆盖.ANGLE算法选择每个方向上最远的可达点作为边界点,并对边界点进行顺(逆)时针连接,构成非凸多边形区域以此作为可达区域. 本文引入了可达区域的面积和轨迹覆盖率作为算法有效性的评价指标,显然,可达区域的面积足够大的时候可以覆盖所有的轨迹,但可达区域的精度较低且不具有实际的应用意义.轨迹覆盖率则是可达区域内的目标轨迹数与所有目标轨迹数的比值,在面积相同情况下,轨迹覆盖率越高意味着更好的算法性能. 以王府井为查询时空点的起始位置,计算不同起始时间的可达区域和轨迹覆盖率,以此来评估RAC,GRAHAM和ANGLE方法的性能,其结果如图4所示. 图4 不同起始时间的计算结果 如图4(a)所示,由RAC,GRAHAM,ANGLE方法计算得到的可达区域面积随着起始时间的不同呈现出不同的特点,但GRAHAM和ANGLE计算得到的可达区域面积总是比RAC大250-350平方公里.由于城市交通的急剧变化,GRAHAM和ANGLE的可达区域面积在几个时间段内剧烈波动,例如上午10点至下午3点.显然,经过可达点的合并以及最大轨迹抵达数的边界选择策略,RAC在不同起始时间总是比GRAHAM和ANGLE得出更小且稳定的可达区域.此外,在交通高峰时期,如上午8:00至9:00和下午6:00至7:00,RAC的可达区域面积有显着变化,可以敏锐地捕捉出随着交通情况的改变引起的可达区域变化. 为了更好地说明开始时间的影响,本文可视化分析起始时间为上午4:00、上午10:00、下午6:00和下午11:00的可达区域,结果见图5. 如图5所示,与GRAHAM方法和ANGLE方法相比,在上述4个起始时间中,RAC总体上得出更小的可达区域.同时,如图5(a)和图5(c)所示,当起始时间为上午4时和下午6时,可达区域均覆盖了二环路内的绝大多数区域,差异体现在主干道路上(图中部的东西向道路复兴路),这是由于上午4时车辆在主干道的速度往往要比下午6时高,因此在贯穿城区的主干道东西方向上能够到抵达更远的位置.此外,如图5(b)和图5(d)所示,当起始时间为上午10时和下午11时,RAC具有更大且相对稳定的可达区域,覆盖了三环内大部分区域.综上所述,不同起始时间的可达区域差异主要集中在主干道路和高速公路附近,而环路内的可达区域随时间推移相对稳定. 图5 王府井在不同起始时间的可达区域 为了验证本文提出的计算方法的高效性,针对不同规模的初始可达点集,分析GRAHAM方法、ANGLE方法和RAC方法的运行效率.其中,以王府井为查询时空点的起始位置,剩余实验参数同表2,依据表2的查询时间段对初始可达点集进行规模划分,最终划分目标轨迹的数量为2500条至20000条的10个不同规模数的目标轨迹数据集.如图6所示,GRAHAM方法和ANGLE方法与本文的RAC方法有着明显的性能差距,尤其是在目标轨迹数量较大时,RAC方法显示出极短的运行时间,这是由于GRAHAM和ANGLE采取循环遍历可达点来寻求边界点的方法,因此随着数据的增大运行时间呈现急速增长的趋势.而RAC通过合并在同一覆盖路段上的可达点操作大大减少了边界路段的计算时间,随着目标轨迹数的增加RAC保持着较短的运行时间.综上所述,RAC在不同规模数据集上的运行效率远远优于GRAHAM方法和ANGLE方法. 图6 算法运行时间结果 除了5.1节讨论的王府井,本文对其他三个典型的城市功能区内的起始位置进行了实验,包括大型公共交通枢纽北京火车站、大型居民住宅区天通苑和大型科技办公区中关村.不同起始位置的可达区域面积和轨迹覆盖率的结果如图7所示. 从图7(a)看出RAC的可达区域面积在大部分起始时间保持稳定,这是因为选择从北京火车站出发的出租车的目的地总是相对均匀地分布在城市中.如图7(d)所示,RAC以北京火车站为起始位置的轨迹覆盖率比较稳定,特别是在上午9:00至下午5:00之间,这是由于北京火车站位于市中心,受早晚高峰影响,这个时间段的可达区域相对集中,轨迹覆盖率更加稳定.在图7(b)和图7(c)中,RAC的可达区域在起始时间为上午8时到9时和下午6时到8时显示相反的趋势,这是因为大多数人早高峰时从居民区天通苑离开,而晚高峰时从中关村工作地点回家.二者的轨迹覆盖率在图7(e)和图7(f)中显示出类似的趋势. 图7 不同起始位置的可达区域面积和轨迹覆盖率结果 为实现定量分析,当起始位置为北京火车站、天通苑和中关村时,本文统计了RAC、GRAHAM和ANGLE在24个起始时间的平均可达区域面积和轨迹覆盖率,其结果列于表4中. 表4 平均可达区域和轨迹覆盖率 Table 4 Statistical results with different starting locations 平均面积(sq.km.)RACGRAHAMANGLE平均轨迹覆盖率(%)RACGRAHAMANGLE北京火车站78.74500.48377.5274.4810095.19天通苑 91.19523.93408.0473.8810095.50中关村 66.27490.03399.7274.2310095.72 从表4看出,GRAHAM和ANGLE在不同的QP起始位置情况下计算的可达区域面积比RAC大得多.以GRAHAM和ANGLE的可达区域面积和轨迹覆盖率的平均结果为参照,RAC的可达区域面积仅是传统方法的30%,同时覆盖了74%的目标轨迹.总的来说,RAC方法较传统方法输出更准确的可达区域. 针对现有城市可达性相关研究对时空特性的分析不足,本文提出一种基于大规模富有时空信息的出租车轨迹数据和道路数据的城市可达区域计算方法(RAC).首先,根据查询时空点的时间和空间约束,从轨迹集中选择在查询时间段内的目标轨迹,并为每个目标轨迹计算唯一的可达点以简化后续步骤.然后将可达点匹配到路段得到覆盖路段,合并同一覆盖路段上的邻近可达点以降低数据冗余.最后,通过基于最大轨迹抵达数的边界路段选择策略,在覆盖路段中选择出最大机会抵达的边界路段,提高可达区域的精度.基于北京市34040辆出租车1个月的真实轨迹数据和2000多条道路数据的实验结果表明,与传统方法相比,RAC计算得到更准确的可达区域且在不同规模数据集中拥有稳定且高效的执行效率.后续,将对城市中不同类型的应用进行研究,优化可达区域边界路段的选择,进一步提高RAC的适用性.4.4 算法性能分析
5 实 验

5.1 查询时空点中起始时间的实验分析
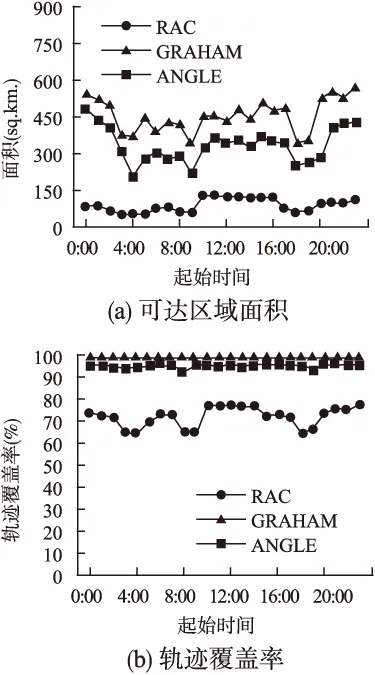
5.2 算法运行时间分析
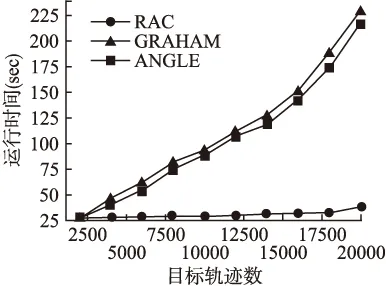
5.3 查询时空点中起始位置的影响
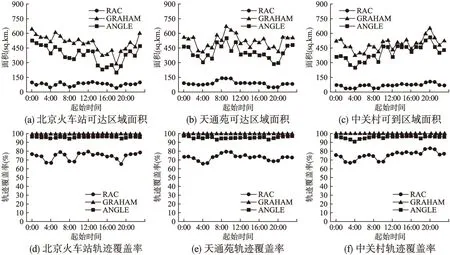
6 总 结

