试卷结构的多维度研究:主成分分析的视角
宋吉祥 李付鹏 杜海燕
目前大多数测验分析集中在试题难度、区分度以及试卷信度等方面,对试卷结构维度的分析相对较少。实际上,无论是在试题编制阶段还是分数统计阶段,研究者都需要对测验结构的维度进行分析。试题编制阶段的测验结构分析主要探讨试题是否达到预定的考试目标,避免无关维度的考查;分数统计阶段的测验结构分析主要探讨试题的实测结果是否达到预定要求。利用主成分分析(Principal Component Analysis,PCA)技术可以实现测验结构维度的检验。本研究以一份综合了数学和英语学科的分类考试试卷的实测数据为例,借助主成分分析技术,进行试卷结构的维度分析,抽取出试卷考查的主要维度。
一、主成分分析的基本思想
主成分分析是一种在损失少量信息的前提下,把数据的多个指标转换为几个综合指标的多元统计分析方法,核心是数据降维,降维后的综合指标称为主成分,每个主成分都是众多原始变量的线性组合,且每个主成分之间互不相关。对于试卷结构的主成分分析而言,通过考试数据降维分析,将一份试卷的考查维度减少到几个主要的维度。本文以试卷结构分析为例,对主成分分析的基本思想进行介绍。
对于给定的某个考生i 在试题j 上的得分记为xij,假设共有n 个考生参加考试,试卷共有p个试题,那么得分矩阵可记为:
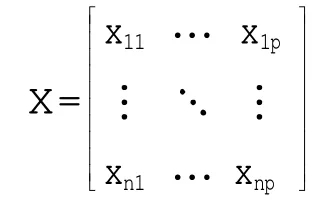
对上述矩阵进行线性变换,形成p 个新变量F1,F2,…,Fp,这些新变量可视为试卷所反映的各个成分,新变量可由原始变量线性表示为:
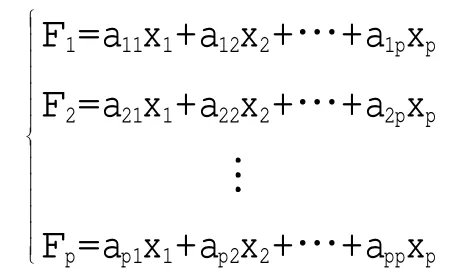
上述变换满足以下条件:
(1)Fi和 Fj互不相关(i≠j;i,j=1,2,…,p);
(2)F1的方差大于 F2的方差,F2的方差大于F3的方差,以此类推,Fp-1的方差大于Fp的方差;
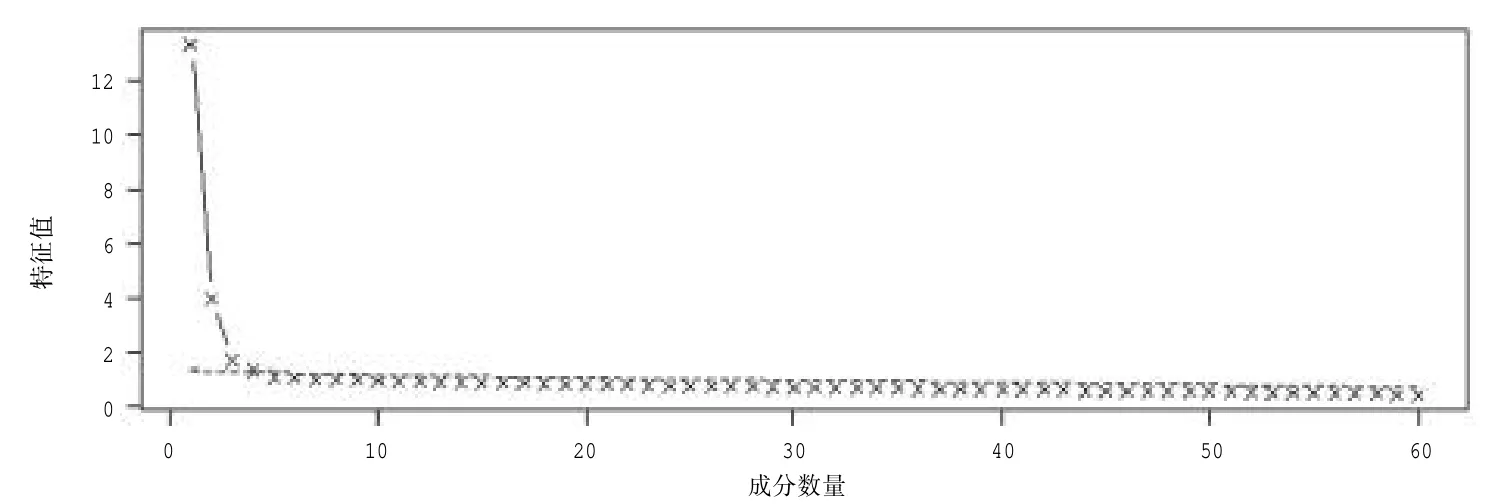
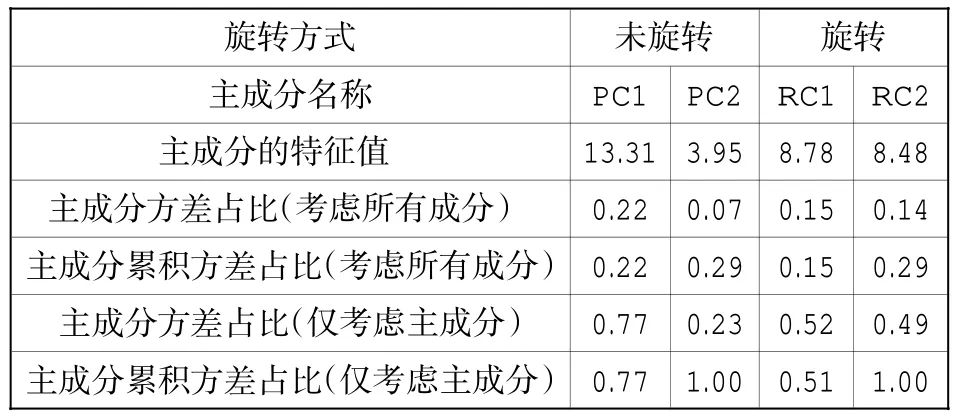
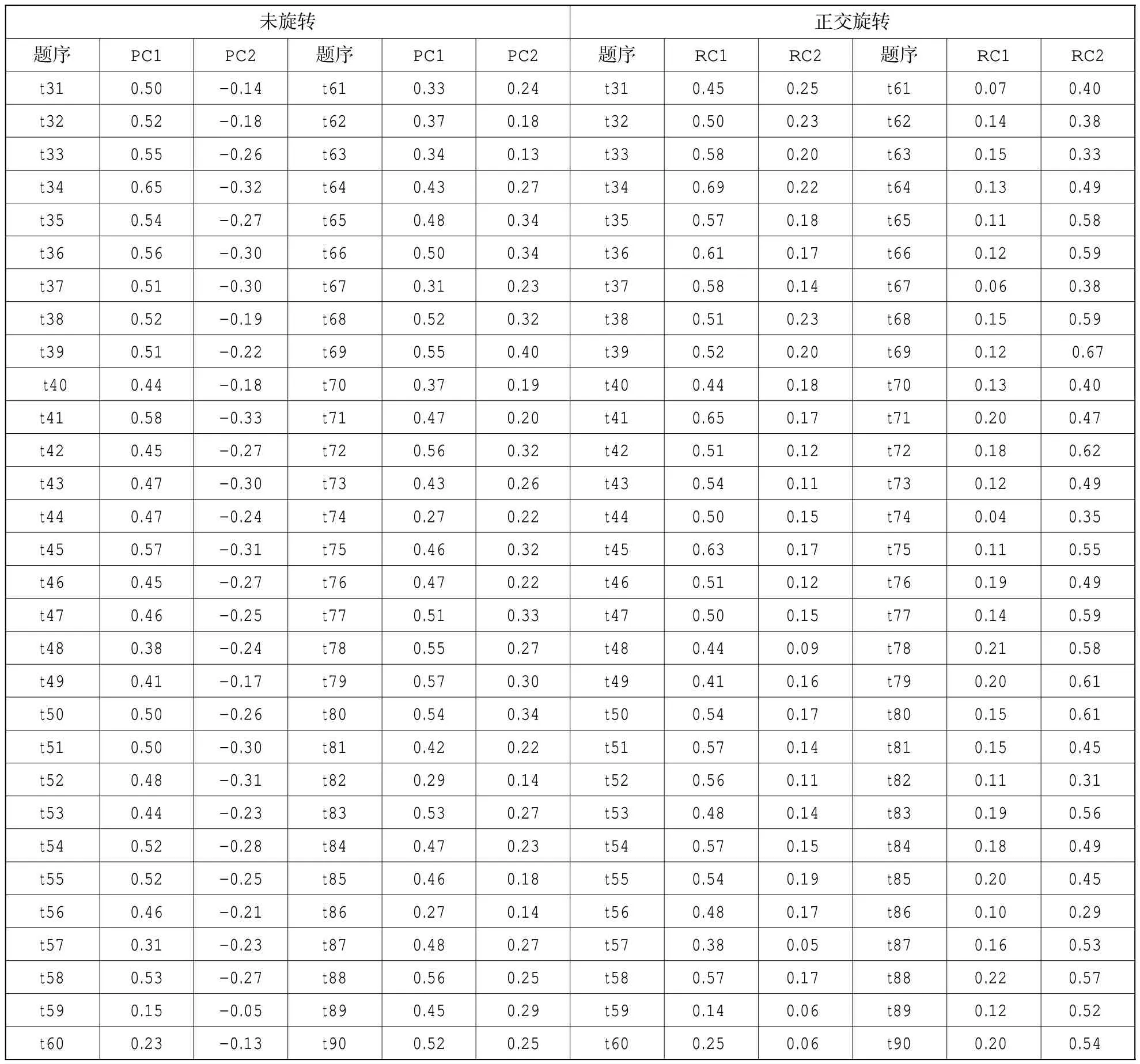
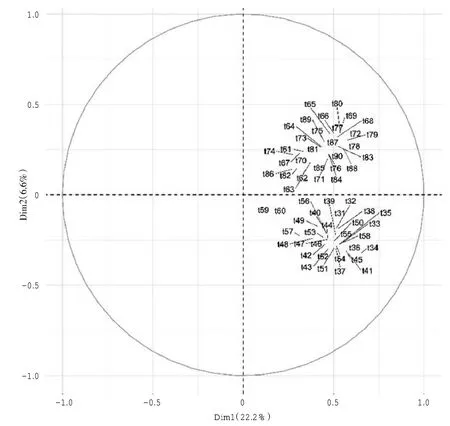
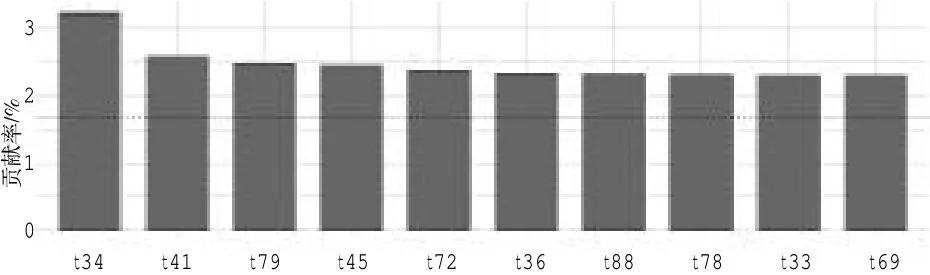
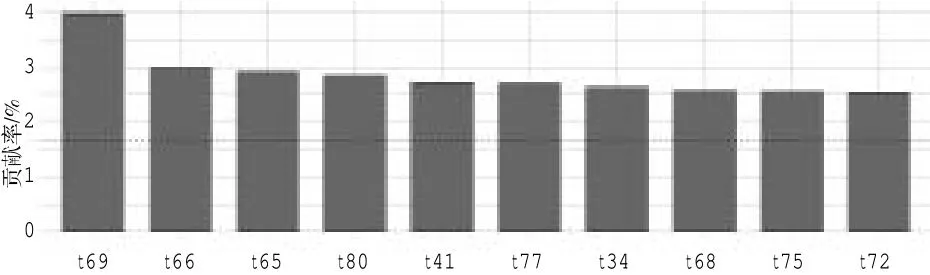
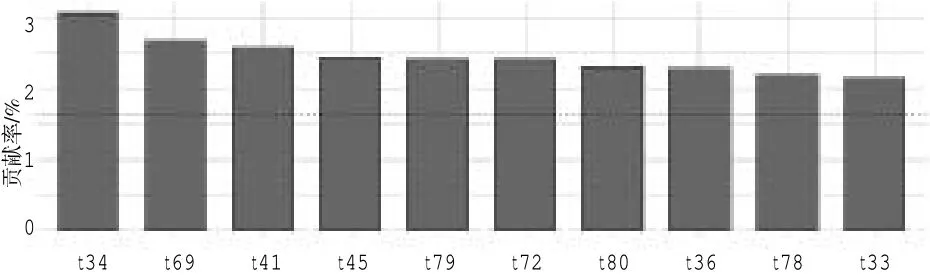
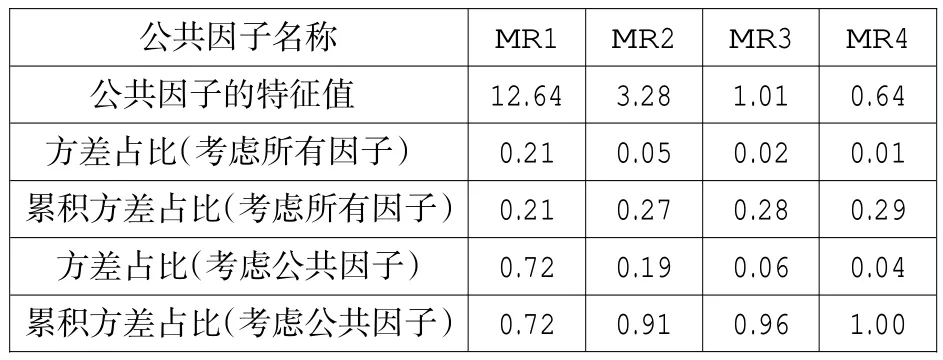
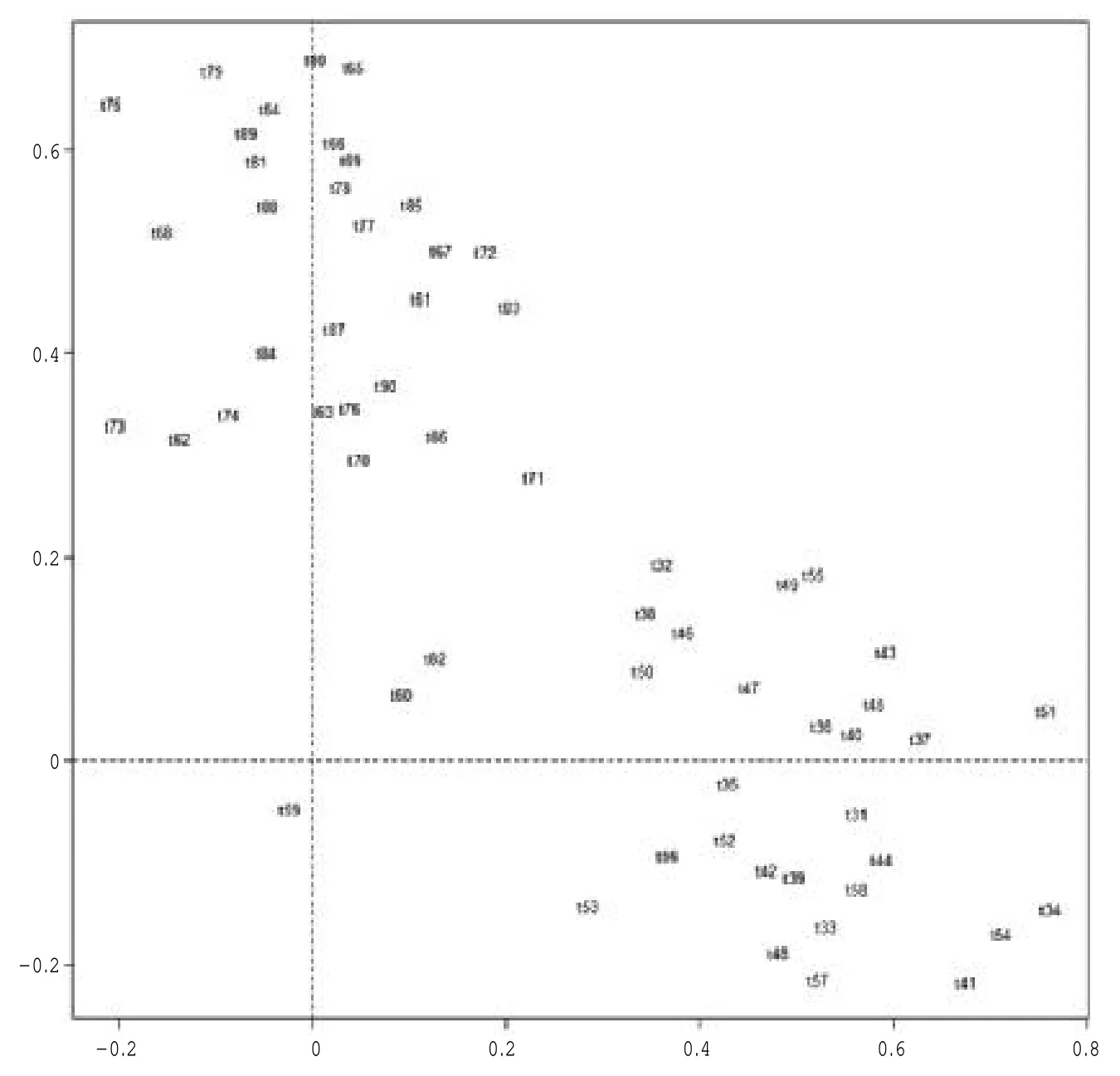
基于以上3 个条件,得到的新变量F1,F2,…,Fp分别称之为原始变量的第一、第二……第p个主成分。主成分分析的思想就是将n 维特征映射到k 维上(k 本研究以一份综合了数学和英语学科的分类考试试卷的考生成绩作为分析对象,探讨主成分分析方法是否能够检验出两个不同的学科试卷维度。每个学科各30 道试题,均为四选一的单项选择题。从考生成绩总样本中抽取了2000 个样本。试题正确作答记1 分,错误作答记0 分。 本研究选择了近年来发展较为迅速的R 语言[1]统计软件包作为分析工具。由于R 语言是一种开源软件,其中的统计分析工具基本上由世界各地的软件开发人员自行以“Package”的形式发布,不同的开发人员可以开发出相同功能的多个工具,也就是说,实现主成分分析的R 语言软件包非常多,这里使用了“Psych”“FactoMineR”和“Factoextra”等软件包。 主成分的判断方法比较多,最常用的是基于特征值的方法。[1]每个主成分都与相关系数矩阵的特征值相关,第一主成分与最大的特征值相关,第二主成分与第二大的特征值相关,依此类推。Kaiser-Harris 准则建议保留特征值大于1 的主成分。Cattell 碎石检验绘制了特征值与主成分的关系图形,在图形变化最大处之上的主成分都保留。平行分析则依据与初始矩阵相同大小的随机数据矩阵来判断要提取的特征值,若基于真实数据的某个特征值大于一组随机数据矩阵相应的平均特征值,则该主成分可以保留。[1] 图1 给出了反映特征值和主成分对应关系的碎石图,同时图中也给出了平行分析的结果。从图1 可知,试卷存在两个明显的主成分,此外,还存在两个特征值略大于1 的主成分。从各维度特征值和方差占比来看:前两个成分分别解释了22.20%和6.60%的方差,所有特征值大于1 的成分累积方差仅占41%;除了前两个成分,其他的成分可解释的方差几乎相当,只有前两个成分与其他成分有明显的区别。基于这一结果,同时结合碎石图、平行分析和Kaiser-Harris 准则,我们确定前两个成分为主成分。需要指出的是,主成分分析提取主成分的方差占比一般要达到80%以上。 根据上述确定的两个主成分,表1 和表2 分别给出了未旋转和正交旋转后的主成分分析数据,表1 给出了主成分方差解释的相关数据,表2给出了主成分与因子(试题)的载荷情况。 由表1 可知,旋转前后的两个主成分的特征值之和没有发生变化,两个主成分在所有成分中的方差占比也没有发生变化。从表2 可知:未旋转前第一主成分PC1 与所有试题的相关均为正相关,相比于第二主成分PC2,第一主成分PC1的载荷较大;第二主成分PC2 与t31~t60 负相关,与 t61~t90 正相关。从试卷结构可知,t31~t60 全部是数学试题,t61~t90 全部是英语试题。上述未旋转的主成分表明,试卷存在一个较大的主成分,以及一个相对较小但不可忽视的主成分,其中第二个主成分完全把数学和英语学科的试题分成两个部分,该主成分表现出明显的学科特征。正交旋转后,主成分RC1 与数学试题的相关度较高,主成分RC2 与数学试题的相关度较低,主成分RC2 与英语试题的相关度较高,主成分RC1 与英语试题的相关度较低,即正交旋转后的主成分分析给出了较为明显的两个主成分。因此,旋转的主成分分析把两个学科的试题几乎完全分离开,进一步验证了未旋转主成分分析所给出的结果,即两个学科呈现出不同的维度。 图1 碎石图 表1 主成分描述性统计 由上述分析可知,对主成分进行旋转可以使结果更具解释意义,其目的是去除数据中与主成分相关性较弱的其他成分。这里采用的是方差极大正交旋转,对两个主成分的每一列尽量只有一组有限的变量来解释。 图2 变量相关圆图显示了变量(试题)间的关系,图中试题坐标与圆心的距离显示了该试题与主成分的相关性,与相关圆的圆心距离较远的试题对主成分的贡献更大一些。图2 中,相关圆图把试题分在了两个不同的象限,同一学科试题分布在同一个象限,并呈对称关系。由于同一学科试题的分布相对集中,为了不使图中试题标签重叠,从而更加清晰地观察试题在相关圆中的分布,笔者在绘图时采用技术处理,将题目标签做了相对移动,试题标签原位置在该试题标签所属直线的另一端点处。图2 显示:英语学科的试题分布在第一象限,数学学科的试题分布在第四象限;数学t34、英语t69 与相关圆的圆心距离,相比于其他试题更远一些,因此,这两道试题对前两个主成分的贡献更大。 表2 主成分载荷 图2 变量相关圆图 主成分是从变量(试题)中提取出来的,找出对两个主成分影响最大的变量(试题),是主成分分析最为重要的问题之一。图3 和图4 分别给出了对两个主成分最具影响力的前10 个试题的直方图:对第一个主成分影响最大的前10 个试题依次是 t34、t41、t79、t45、t72、t36、t88、t78、t33、t69,数学和英语试题各占5 题;对第二个主成分影响最大的前 10 个试题依次是 t69、t66、t65、t80、t41、t77、t34、t68、t75、t72,英语试题稍多一些。对影响两个主成分的变量(试题)进行对比发现,部分试题对两个主成分都产生了较大的影响(t34、t41、t72、t69)。图3 和图4 中的虚线表示所有试题预期的平均贡献。图3 和图4 分别显示了数学t34 对第一个主成分的贡献最大,英语t69 对第二个主成分的贡献最大。这与图2 相关圆图中的分析结果具有一致性。试题对两个主成分(如RC1 和RC2)的总贡献可按照下列公式[2]计算: 其中,C1和 C2分别是变量对RC1 和 RC2 的贡献,Eig1和 Eig2分别是RC1 和RC2 的特征值。按此计算,对第一个和第二个主成分总贡献最大的前10 个试题依次分别是t34、t69、t41、t45、t79、t72、t80、t36、t78、t33,数学和英语试题各占5 题。试题对两个主成分的贡献如图5 所示:对于前两个主成分,数学t34 和英语t69 分别是数学和英语学科中贡献最大的试题。 图3 第一主成分变量贡献图 图4 第二主成分变量贡献图 图5 第一和第二主成分变量贡献图 为确保上述检验结果的稳定性,笔者从实验样本所在的总样本中采取无放回方式,分别抽取10 组样本,每组样本量均为2000,按照完全相同的方法进行验证性实验分析,若这10 组实验结果与上述实验结果基本一致,则说明实验结果具有一定的稳定性。 试卷结构多维度的研究方法比较多,除了主成分方法,常见的方法还包括验证性因素分析(CFA)[3]、探索性因素分析(EFA)[4]等。为验证本文所使用的主成分分析结果的有效性,笔者采用探索性因素分析对上述数据进行实验模拟。主成分分析和因素分析具有本质的区别,是两类不同的分析方法,但分析流程基本类似,都可以进行试卷维度的因素分析。探索性因素分析是探究一组观察变量的变异能否由少数潜在变量的线性组合来表示的分析方法,通过求解共同因素部分中的因素载荷和因素得分,来探索由这些因素组成的数据结构。 表3 未旋转公共因子载荷及其占比 图6 斜交因素分析图 表3 列出了探索性因素分析前4 个未旋转公共因子载荷及其占比。其中,前2 个公共因子(MR1 和 MR2)的载荷明显大于第 3 个因子(MR3)和第4 个因子(MR4)。从所有因子载荷方差占比来看,前 2 个因子(MR1 和 MR2)的累积方差占比仅为27%左右,不能解释试卷主要的或大部分的信息。但从表3 也可以看出的是:选择前4 个因子,累积方差占比仅为29%左右,并没有提供更多的信息;如果选择4 个因子,前2 个公共因子(MR1 和MR2)的累积方差占比达90%左右,而第 3 个因子(MR3)和第 4 个因子(MR4)的方差占比仅为10%左右,从测验结构维度的简单性来考虑,选择2 个因子较为适宜。 图6 为公共因子的探索性因素分析的斜交因素分析图,直观地呈现出两个学科试题的分离:同一学科的试题基本上聚集在一起;数学学科的试题主要聚集于公共因子ML1,说明数学试题受公共因子ML1 的影响较大;英语学科试题主要聚集于公共因子ML2,说明英语试题受公共因子ML2 的影响较大。旋转之后的几个拟合度指标如下:RMSR=0.03,TLI =0.928,RMSEA =0.025。以上拟合指标表明试卷两个维度的模型较好地拟合了测验数据。 实验结果表明,主成分分析可以将两个学科的试题相互分离,从而确定试卷具有两个主要维度。探索性因素分析与主成分分析结果具有一致性,验证了主成分分析方法对试卷结构多维度分析的有效性。需要指出的是,由于数据所提取的两个主成分占总体可解释的方差较低,主成分难以有效反映试卷结构的信息,说明试卷的效度需要进一步提高。这可能对本研究的结果具有一定影响。 测验的多维度是客观存在的,目前基于单维结构的分析方法难以满足实际需要,利用现有的考试测量技术进行试卷结构的多维度分析具有重要意义。本文利用简单易行的主成分分析技术对一份试卷的结构进行多维分析,表明主成分分析是一种较为有效地分析试卷结构多维度的方法。二、实验设计
1.研究数据基本情况
2.分析工具
3.主成分个数确定
4.主成分分析
5.变量相关分析
6.变量贡献分析
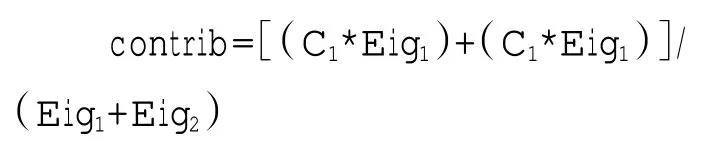
7.与其他方法的比较分析
三、实验结论

