负水头环境土壤水分湿润锋运移三维模拟

朱 君，李 婷，谢 添，张艾明

（中国辐射防护研究院 核环境模拟与评价技术重点实验室，太原 030006）

0 引 言

负水头供水可以精准控制土壤含水率，维持土壤的非饱和状态，避免因干湿交替使植物遭受旱涝胁迫和土壤养分淋溶损失，是开发新型节水灌溉技术的有效措施[1-2]。因此，对负水头条件下土壤水分运动特征的研究，具有十分重要的理论和实践意义。目前，大量的实验结果表明负水头条件下，累积入渗量与时间、最大水平和垂直湿润距离与时间都符合幂函数关系，且湿润体的宽深比随入渗时间和水头的增加而增加[3-6]。Rodriguez-Sinobas等[7]也认为湿润体体积和宽深比随着供水压力的增加而增加，且入渗速度与供水压力呈幂函数关系。以上研究不是建立在土壤水动力学的基础上，是直接拟合试验数据得到的经验公式。如何结合试验现象，确定负水头环境下土壤水分运移模型，并预测不同供水水头、不同土壤质地等条件下灌水器的间距，实现土壤含水率的持续精确控制则更加重要。但是现有模型都只适用于描述负水头条件下土壤湿润锋一维垂直、水平运动规律[8-10]。邹朝望等[11-12]基于Gardner和Russo公式表征了土壤水分特征曲线与非饱和土壤的导水率，推导了负水头下湿润峰、入渗率、累积入渗量与入渗时间的关系，并用试验数据验证了其合理性。范军亮等[13-14]发现Philip模型和Kostiakov公式均可以较好描述负水头条件下，4种典型黄土高原土壤的累积入渗量、湿润锋运移距离、入渗率和入渗时间之间的关系。上官玉铎等[15-16]对比了负水头条件下的土壤水分入渗规律，发现累积入渗量与时间呈幂函数关系，湿润锋与时间的平方根呈线性关系，Kostiakov公式比Philip模型、Green-Ampt模型能更准确描述入渗率和时间的关系。辛琛等[17-18]通过实验获得了不同负水头下累积入渗量、湿润锋和入渗时间的关系，发现Philip模型、Green-Ampt模型和Kostiakov公式都可以描述负水头条件下的土壤湿润锋运移规律。王佳佳等[1]将对土壤湿润锋运移规律的研究拓展到二维模型，利用室内实验观测了不同负压水头条件下土壤水盐的运移特征，通过实验数据验证了Hydrus-2D模型的适用性，对不同质地土壤中水分分布、累积入渗量、水分入渗速率、盐分分布和蒸发量进行了模拟。冀荣华等[19]结合土壤水动力学建立了负压灌溉条件下的Hydrus-2D水分入渗模型，模拟结果与实测结果的相对误差为2%～4%。Yao等[20]通过二维湿润锋实验发现，湿润体近似同心椭球面，且椭球中心含水率最高。现阶段负水头条件下的土壤湿润锋运移模型以一、二维为主[21-26]，三维模型鲜有报道。本文通过室内实验数据验证负水头环境下Hydrus-3D土壤水分模型的准确性和有效性，对完善负水头条件下的土壤水分运动理论十分必要。

1 材料与方法

1.1 仪器与试剂

实验装置由马氏瓶、有机玻璃土箱、多孔板灌水器、橡皮输水管组成。有机玻璃箱为扇形柱体，高40.0 cm，径向长度35.0 cm，夹角30o；多孔板灌水器的出水孔为 3～4 µm（15 cm×10 cm×2.5 cm）；马氏瓶高75.0 cm，内径9.0 cm；橡皮输水管内径6.0 mm。试验采用超纯水（Milli-Q Element超纯水制备机，日本Millipore公司）。

1.2 试验样品

选择山西省榆次地区的砂土、壤土介质为试验对象，用摇摆式筛析机（AS200型，德国Retsch公司）以及激光粒度分析仪（Mastersizer 3000E，英国Malvern公司）测定粒径分布。其中，砂土的砂粒量85.50%、粉粒量 5.47%、黏粒量 9.03%，有机质量1.7 g/kg，土壤pH值8.34。壤土的砂粒量54.21%、粉粒量29.65%、黏粒量16.14%，有机质量9.3 g/kg，土壤pH值8.08。

1.3 土壤水力参数测定

测定砂土、壤土的水分特征曲线与饱和导水率。水分特征曲线采用离心机法测定，由低到高依次设置12个不同的转速对饱和试样进行脱水，得到不同体积含水率下的土壤吸力值。饱和导水率采用定水头法测定，首先从土柱底端通水，使整个土柱体饱和，上部安装定水头装置，调整入水口供水量，使试验期间水头差H保持不变，记录时间Δt和底部出口流量Q。

1.4 试验方法

砂土、壤土均按比例1.25 g/cm3分层装入有机玻璃箱。将马氏瓶、灌水器用橡皮管连接起来，埋入有机玻璃箱的土壤介质中，并保证整套装置的密封性。以多孔板灌水器顶部为参考平面，设计3种不同的作用水头H，如下：

1）H=0 m，作用水头为 0，马氏瓶进气口与灌水器平。

2）H=-0.5 m，作用水头为负压，马氏瓶进气口比灌水器低0.5 m。

3）H=-1.0 m，作用水头为负压，马氏瓶进气口比灌水器低1.0 m。

记录累积入渗量和湿润锋运移曲线。在有机玻璃箱的表面粘贴透明胶片记录水分入渗过程，累积入渗量通过马氏瓶上的刻度读取。

2 结果与分析

2.1 土壤水分湿润锋运移结果

在有机玻璃箱表面粘贴的透明胶片上记录相应时刻砂土、壤土的湿润锋运移过程，并在试验结束后将胶片上的水分运移曲线转化为Excel数据，见图2、图3。

图2 砂土水分湿润锋运移曲线Fig.2 Wetting front moving curve of sand

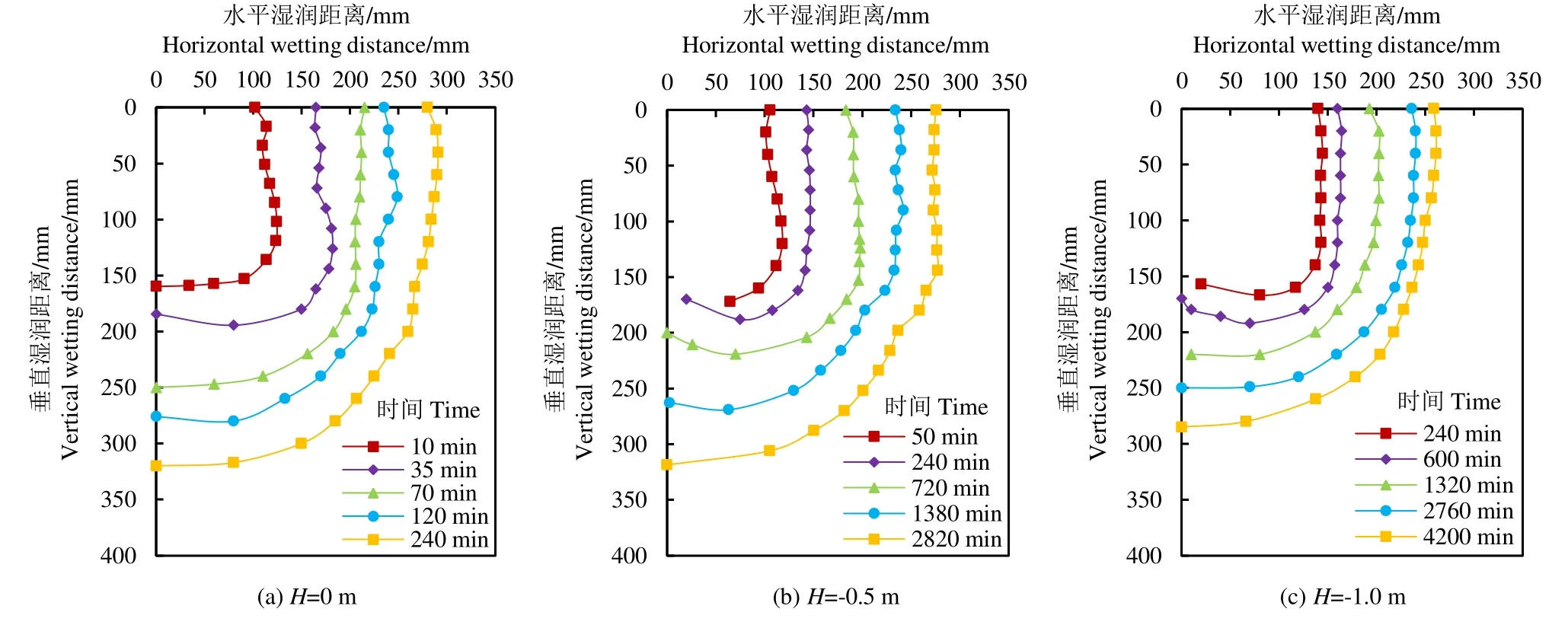
图3 壤土水分湿润锋运移曲线Fig.3 Wetting front moving curve of loam

在重力势和基质势作用下，湿润锋向垂直和水平方向运动，湿润体近似为1/4椭圆状，湿润锋包络面积随时间逐渐增加。

1）H=0 m时，砂土的湿润锋包络面积在30 min到达904.1 cm2，壤土的湿润锋包络面积在240 min到达为791.7 cm2。

2）H=-0.5 m时，3 480 min砂土的湿润锋包络面积到达742.3 cm2，2 820 min壤土的湿润锋包络面积到达745.7 cm2。

3）H=-1.0 m时，4 200 min砂土的湿润锋包络面积到达241.2 cm2，4 200 min壤土的湿润锋包络面积到达629.5 cm2。

2.2 入渗量与时间的关系

3种不同负水头条件下，砂土、壤土的累积入渗量随着时间的增加逐渐增大，结果见图4。可以用幂函数I=m×tn描述累积入渗量与时间的关系，随着负水头高度的增加，m、n值均减小。砂土的m值由66.51减少至1.08，n值由0.96减少至0.42；壤土的m值由38.49减少至6.59，n值由0.69减少至0.56，拟合值见表1。与文献[3-7]的试验结果一致。

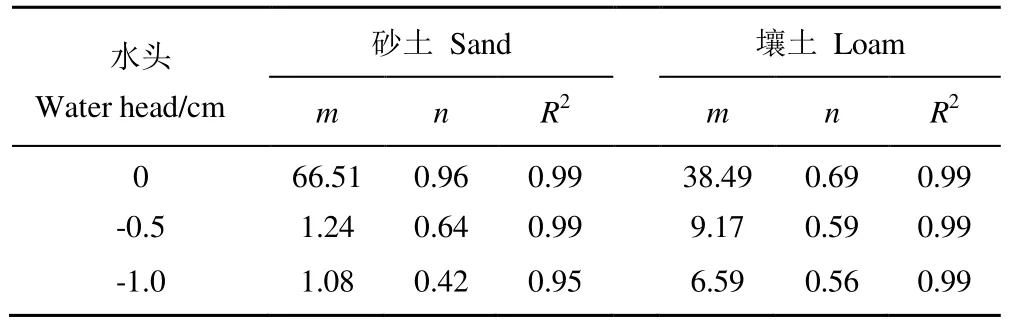
表1 累积入渗量与时间拟合值Table 1 Fitting parameters of cumulative infiltration and time

H=0 m，砂土m值是壤土的172.80%，原因是压力势占主导作用，且砂土的渗透系数大于壤土。H=-0.5 m，砂土m值是壤土的13.52%；H=-1.0 m，m值砂土是壤土的 16.34%，壤土的累积入渗量曲线高于砂土，基质势逐渐占主导作用。

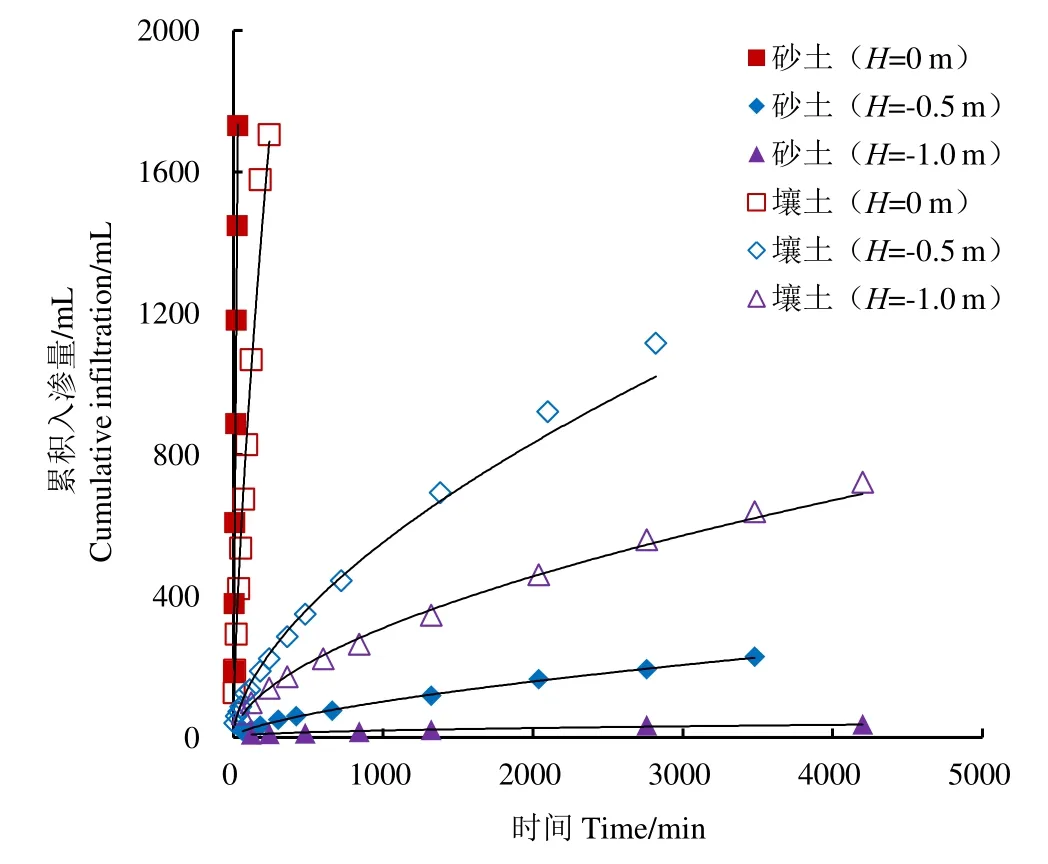
图4 累积入渗量随时间变化曲线Fig.4 Curve of cumulative infiltration versus time

2.3 湿润峰与时间的关系

3种不同负水头条件下，砂土、壤土湿润锋随时间的增加逐渐向水平、垂直方向扩大，结果见图5。水平和垂直最大湿润距离与时间的关系，用下式描述：

式中：Zf为最大湿润距离（mm）；t为时间（min）；p与q为常数，拟合关系见表2和表3。砂土和壤土的水平、垂直最大湿润距离与时间的平方根呈良好的线性关系[15-16]，相关系数R2都大于0.96，p随着负压水头的增加而减小，砂土p值由36.20减少至1.17，壤土p值由13.24减少至2.43。

H=0 m，砂土p值是壤土的273.41%，单位时间砂土湿润锋迁移距离大于壤土，原因是压力势占主导作用。H=-0.5 m，砂土p值是壤土的78.90%；H=-1.0 m，砂土p值是壤土的48.15%，单位时间壤土湿润锋迁移距离大于砂土，基质势逐渐占主导作用。

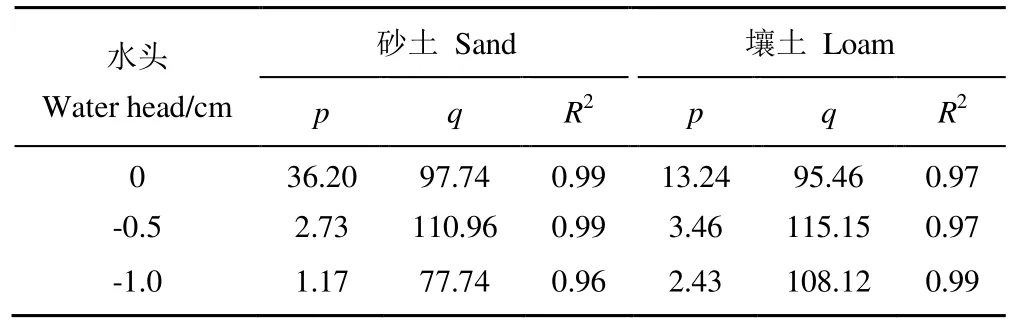
表2 水平最大湿润距离与时间拟合值Table 2 Fitting parameters of maximum horizontal wetting distance and time

表3 垂直最大湿润距离与时间拟合值Table 3 Fitting parameters of maximum vertical wetting distance and time

图5 湿润锋距离与时间变化曲线Fig.5 Curve of wetting distance versus time

图6 湿润锋入渗速度与时间变化曲线Fig.6 Curve of infiltration velocity of wetting front versus time

2.4 入渗速度与时间的关系

负水头高度从0 m增加至-1.0 m时，湿润锋入渗速度逐渐减小，见图6。砂土、壤土的水平湿润锋入渗速度（VH）和垂直湿润锋入渗速度（VV）与时间的关系用下式描述：

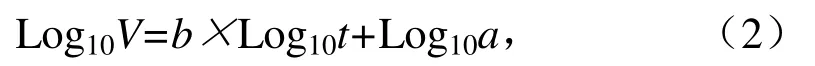
式中：V为湿润锋入渗速度（mm/min）；t为时间（min）；a、b为常数，拟合关系见表4和表5。砂土和壤土的水平、垂直湿润锋入渗速度与时间均呈良好的幂函数关系[3-7]，相关系数R2都大于0.99。

H=0 m，曲线上同一时间点对应的湿润锋入渗速度砂土>壤土；H=-0.5 m和-1.0 m，曲线上同一时间点对应的湿润锋入渗速度壤土>砂土。

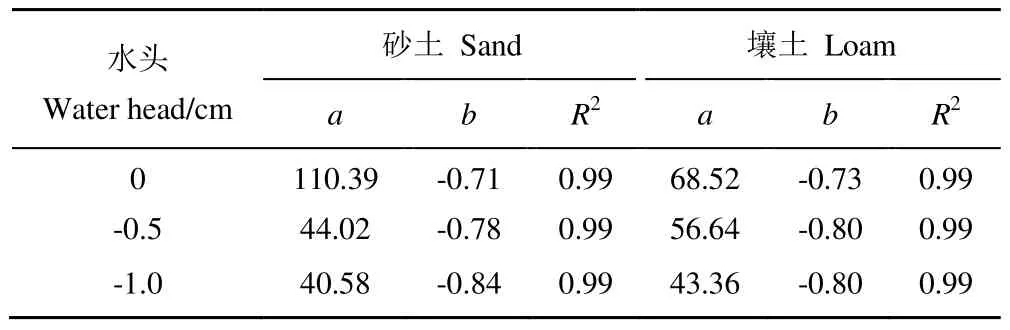
表4 水平湿润锋入渗速度与时间拟合值Table 4 Fitting parameters of infiltration velocity of Horizontal wetting front and time

表5 垂直湿润锋入渗速度与时间拟合值Table 5 Fitting parameters of infiltration velocity of vertical wetting front and time

3 模型与验证

应用 Hydrus-3D建立三维土壤水分运移数值模型[27-29]，通过试验数据验证模型的准确性和有效性。

试验扇形柱体高40.0 cm，径向长度35.0 cm，夹角300。模型在z方向离散为5 mm，剖分为20层，共生成节点数111 383个，三角网格298 711个。计算时间步长为1 s。

3.1 参数选取

根据试验结果，采用Van Genuchten模型对砂土、壤土的饱和含水率θs、残余含水率θr、进气值倒数α和拟合参数n进行求解，同时计算饱和渗透系数。参数结果见表6。

表6 土壤水力参数Table 6 Soil hydraulic parameters

3.2 模型计算结果

将累积入渗量与时间的幂函数关系作为流量边界输入模型，其他边界处理为0流量边界。按照物理模型试验数据对应的时间点输出计算结果，限于篇幅，3种负水头条件下只给出了砂土、壤土最后一个时间点的湿润锋分布。

1）对于砂土，H=0 m时，30 min灌水器周围达到饱和含水率0.47 cm3/cm3，最大的水平、垂直湿润锋距离为290、366 cm；H=-0.5 m时，3 480 min含水率降低至0.202 cm3/cm3，最大的水平、垂直湿润锋距离为278、314 cm；H=-1.0 m时，4 200 min含水率降低至0.129 cm3/cm3，最大的水平、垂直湿润锋距离为154、182 cm。见图7。

图7 砂土水分湿润锋运移计算结果Fig.7 Calculation results of wetting front moving in sand

2）对于壤土，H=0 m时，240 min灌水器周围达到饱和含水率0.503 cm3/cm3，最大的水平、垂直湿润锋距离为289、330 cm；H=-0.5 m时，2 820 min含水率降低至0.487 cm3/cm3，最大的水平、垂直湿润锋距离为289、323 cm；H=-1.0 m时，4 200 min含水率降低至0.443 cm3/cm3，最大的水平、垂直湿润锋距离为261、292 cm。对基质势较大的壤土，随着负水头高度的增加，灌水器周围含水率只降低了11.9 %。结果见图8。

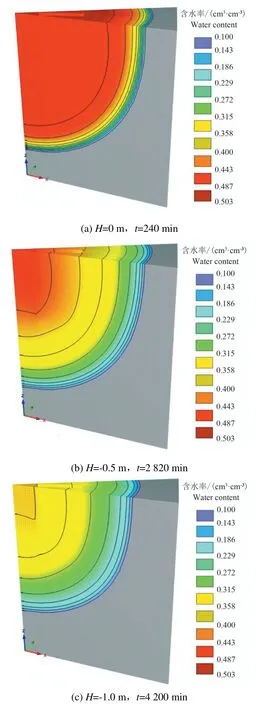
图8 壤土水分湿润锋运移计算结果Fig.8 Calculation results of wetting front moving in loam

3.3 模型验证

3种负水头条件，以负水头高度0 m的实测湿润锋包络面积作为模型率定数据，确定水分运移模式和参数等；然后，只改变流量边界，即累积入渗量与时间的幂函数关系，以负水头高度-0.5 m和-1.0 m的实测湿润锋包络面积作为模型验证数据。见图9、图10。

由表7可知3种负水头模型，砂土计算湿润锋包络面积与实测湿润锋包络面积的偏差 0.51%～7.21%。由表8可知壤土计算湿润锋包络面积与实测湿润锋包络面积的偏差0.22%～16.03%。所建三维模型可以用于描述负水头环境下土壤水分湿润锋的运移特征和规律。

表7 砂土模型验证结果Table 7 Results of sand model validation

表8 壤土模型验证结果Table 8 Results of loam model validation

图9 砂土水分湿润锋运移模型验证Fig.9 Model verification of wetting front moving in sand

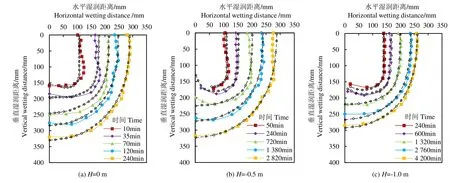
图10 壤土水分湿润锋运移模型验证Fig.10 Model verification of wetting front moving in loam

3.4 湿润深度和湿润体体积

负水头灌溉的优势是可以控制土壤含水率，维持非饱和状态，通过率定和验证后的模型，可以得到不同负水头、不同灌水时长条件下，各含水率的湿润深度及湿润体体积的动态变化（表9、表10）。

1）砂土负水头高度H=0 m时，6～30 min灌水器周围的湿润深度由20.5 cm增加至36.7 cm，湿润体体积由1 227.95 cm3增加至5 909.18 cm3。含水率0.376～0.344的湿润深度由18.0 cm增加至30.6 cm，湿润体体积由763.02 cm3增加至2 829.91 cm3，占总体积的62%减少至48%。

负水头高度H=-0.5 m时，3 480 min后湿润深度为31.5 cm，湿润体体积为4 478.77 cm3，最大含水率为0.162。负水头高度H=-1.0 m时，4 200 min后湿润深度为31.5 cm，湿润体体积为820.68 cm3，最大含水率为0.103。

2）壤土负水头高度H=0 m时，10～240 min灌水器周围的湿润深度由16.5 cm增加至33.0 cm，湿润体体积由345.51 cm3增加至5114.94 cm3。含水率0.402～0.390的湿润深度由15.05 cm增加至30.6 cm，湿润体体积由189.07 cm3增加至2 262.82 cm3，由占总体积的55%减少至44%。

负水头高度H=-0.5 m时，50～2 820 min灌水器周围的湿润深度由21.0 cm增加至32.8 cm，湿润体体积由484.66 cm3增加至5 015.60 cm3。含水率0.354～0.218的湿润深度由15.45 cm增加至29.95 cm，湿润体体积由256.09 cm3增加至3 521.29 cm3，由占总体积的53%增加至70%。

负水头高度H=-1.0 m时，240～4 200 min灌水器周围的湿润深度由17.5 cm增加至28.75 cm，湿润体体积由654.44 cm3增加至3 572.29 cm3。含水率0.320～0.183的湿润深度由16.25 cm增加至26.35 cm，湿润体体积由510.16 cm3增加至2 681.76 cm3，由占总体积的75%～78%。

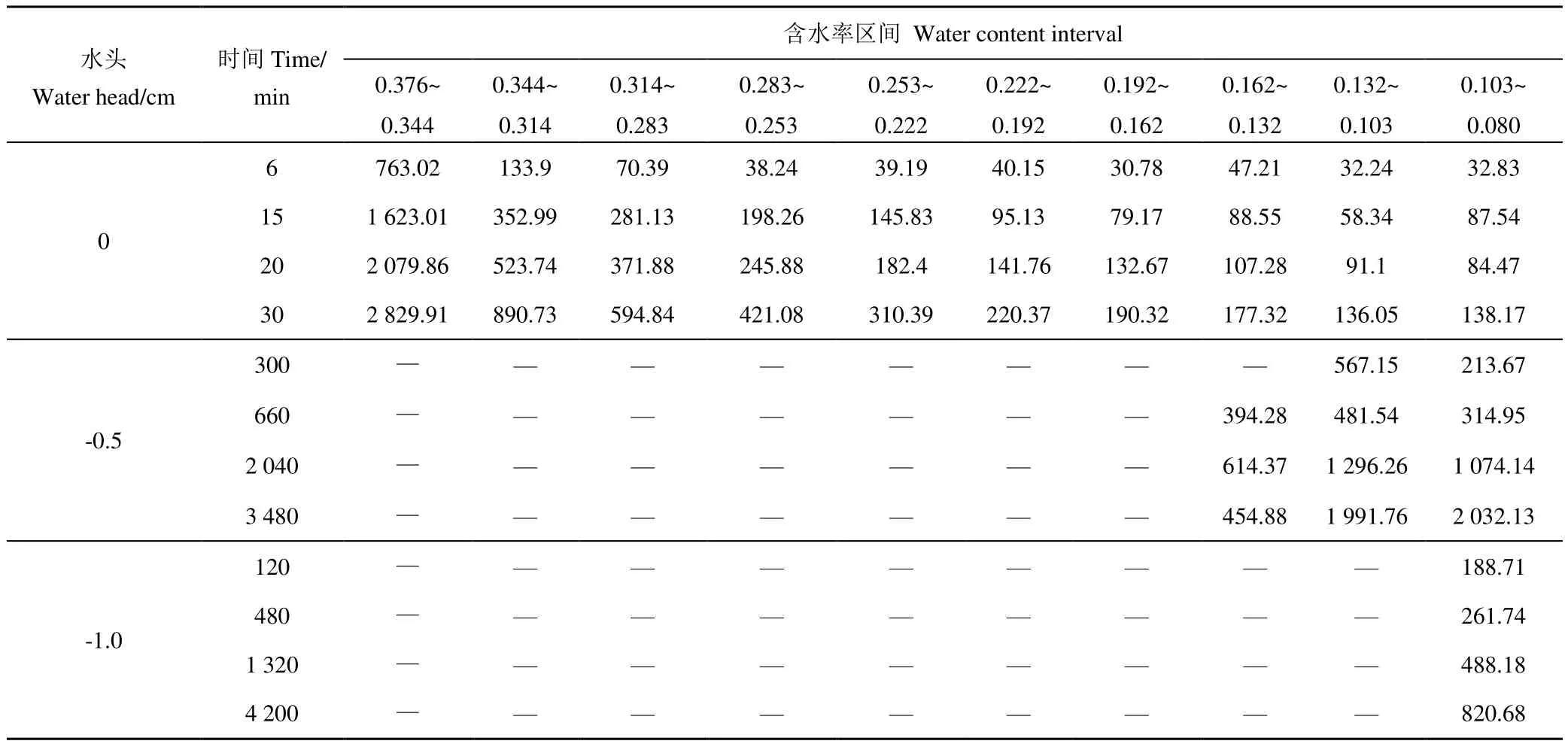
表9 砂土湿润体体积随时间的动态变化情况Table 9 Dynamic change of wetting volume of sand with time cm3

表10 壤土湿润体体积随时间的动态变化情况Table 10 Dynamic change of wetting volume of loam with time cm3

由试验和模拟结果可知，砂土负水头高度H=0 m时，湿润体48%～62%接近饱和含水率；H=-0.5 m时，湿润体的最大含水率为16.2%。砂土的负水头灌溉高度应介于-0.5~0 m之间较为合理。

壤土负水头高度H=-0.5 m时，2 820 min后含水率0.286～0.218的湿润深度为29.95 cm，湿润体的体积为1 891.96 cm3，占总体积的38%；H=-1.0 m时，2 760 min后含水率0.286～0.218的湿润深度为23.5 cm，湿润体体积为1 434.91 cm3，占总体积的40%。壤土的负水头灌溉高度可以介于-1.0～-0.5 m之间。

4 结 论

1）砂土、壤土的累积入渗量随着时间的增加而逐渐增大，呈良好的幂函数关系。H=0 m，砂土的累积入渗量曲线高于壤土；H=-0.5 m或者-1.0 m，壤土的累积入渗量曲线高于砂土。

2）砂土、壤土的湿润锋随着时间的增加逐渐向水平、垂直方向扩大。水平、垂直最大湿润距离与时间的平方根呈良好的线性关系。H=0 m，单位时间内砂土湿润锋迁移距离大于壤土；H=-0.5 m或者-1.0 m，单位时间内壤土湿润锋迁移距离大于砂土。

3）砂土、壤土的湿润锋入渗速度随着负水头高度的增加逐渐减小，与时间呈良好的幂函数关系。H=0 m，曲线上同一时间点对应的湿润锋入渗速度砂土>壤土。H=-0.5 m或者-1.0 m，曲线上同一时间点对应的湿润锋入渗速度壤土>砂土。

4）应用Hydrus-3D软件，建立三维土壤水分运移数值模型。率定和验证后的模型计算湿润锋包络面积与实测的偏差，砂土为 0.51%～7.21%，壤土为0.22%～16.03%，所建三维模型可以计算不同负水头、不同灌水时长条件下，各含水率的湿润深度及湿润体体积的动态变化。