考虑剪力滞效应的变截面箱梁桥固有频率及其影响研究

□文/耿文宾 高 璞 周俊龙

变截面连续箱梁桥是装配式桥梁的结构形式之一，为满足路线设计和结构设计要求，变截面连续箱梁已得到广泛应用[1]。同时，箱梁桥与剪力滞效应相关的系列安全问题[2]引起了广泛的关注和研究。

目前，关于变截面箱梁考虑剪力滞效应的静力学计算理论较为完善，但关于考虑剪力滞效应的动力学研究的成果较少。甘亚南等[3～4]基于哈密顿原理研究了剪力滞效应对多种类型等截面箱梁桥固有频率的影响。吴有俊等[5]利用能量变分原理对考虑剪力滞效应的简支箱梁进行了自振特性研究。张永健[6～7]推导出考虑剪力滞效应不同箱梁模型固有频率的解析解，对固有频率关于不同宽跨比的规律和影响程度进行了研究。张琪等[8]提出一种用于考虑剪力滞效应曲线等截面箱梁固有频率求解的有限段法，总结了固有频率与宽跨比和曲率半径变化的一般规律。用于等截面箱梁剪力滞效应分析的理论不能直接用于变截面箱梁结构，因此，关于变截面连续箱梁剪力滞效应研究的理论方法有待进一步研究。

本文提出一种适用于变截面连续箱梁考虑剪力滞效应固有频率计算的三节点梁段法，基于最小势能原理推导出梁段法的等参有限元行列式，编写了有限元计算程序。通过工程实例验证理论公式和程序编写的正确性和适用性。

1 坐标系及基本假定

在竖直对称的变截面梯形箱梁段上，建立笛卡尔坐标系（x，y，z），坐标系中箭头所指方向为坐标轴正方向，S为箱梁闭合截面壁厚中心线的方向；箱梁横截面顶板、底板和悬臂板的宽度分别为bt、bb和bp，相应的厚度分别为t1、t2和t3，yC和yN分别为箱梁截面形心C和扭转中心N的竖向坐标，h（z）为截面z处箱梁的高度，ht和hb分别为形心轴距顶板和底板中心线的距离。见图1。

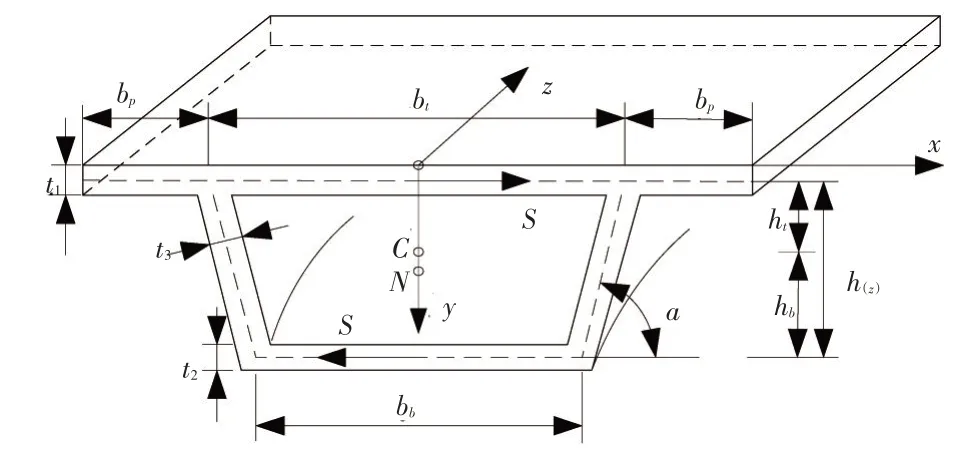
图1 坐标系及几何参数

2 箱梁内任意点位移和应变

2.1 基本变形和空间位移

考虑扭转翘曲和剪滞翘曲的影响，变截面箱梁段任意点的空间位移为

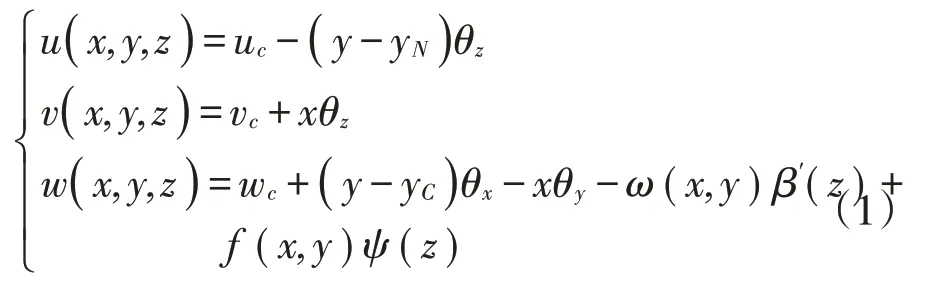
式中：uc，vc，wc——截面沿x，y，z方向的位移；

θx，θy，θz——截面绕x，y，z轴的转角；

ω（x，y）——箱梁闭合截面中线的主扇形坐标；

β’（z）——扭转翘曲位移变量的一阶导数；

f（x，y）——二次型的剪力滞翘曲位移函数[9]；

ψ（z）——截面剪切变形的最大差值。

2.2 应变和位移关系

箱梁截面上任意点的正应变εz、剪应变γzs与空间位移场函数的关系为

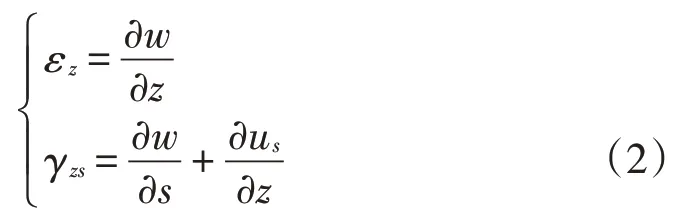
式中：uS——闭合截面内任意点沿S方向的位移，各翼板us的具体表达式参考文献[10]。

式（1）中：yC，yN，ω和f为关于z的变量，各翼板的正应变为

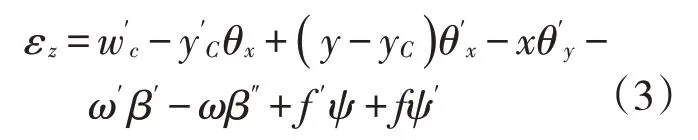
各翼板的剪应变为

顶板

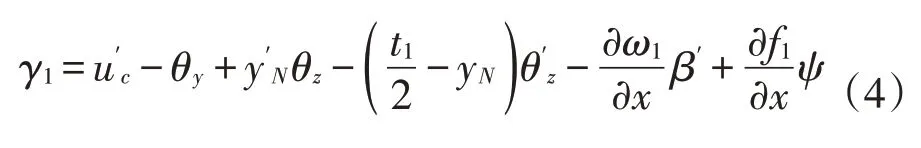
右腹板

底板

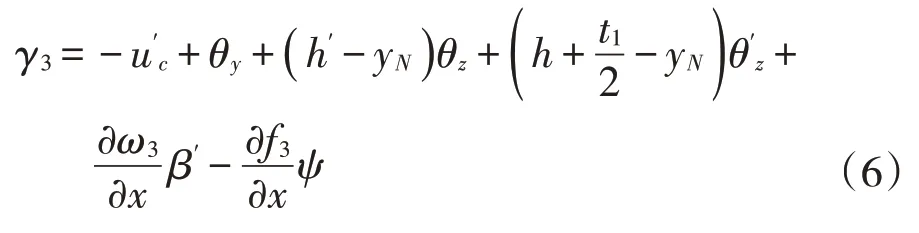
左腹板

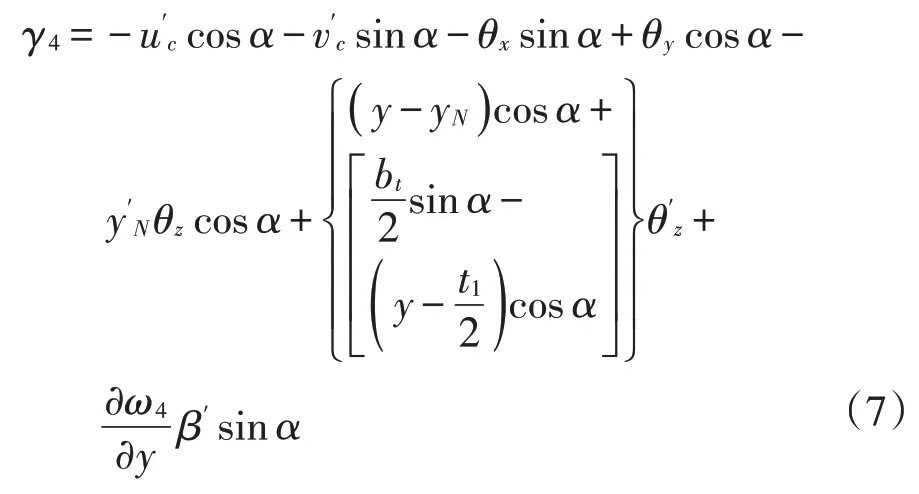
3 有限单元列式

3.1 形函数

选用C0连续的二次抛物线形函数，形函数及其关于ζ一阶导数的表达式为

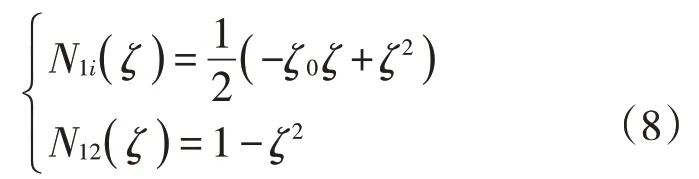
式中：i=1时，ζ0=1；i=3时，ζ0=-1。

广义局部坐标和整体坐标导数变换关系的雅克比系数J为

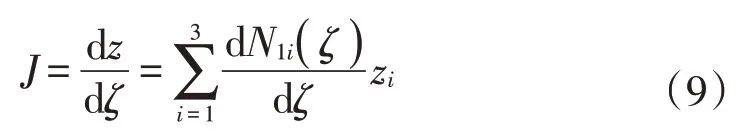
3.2 单元刚度矩阵

单元内任意截面ζ上的位移与节点基本关系为

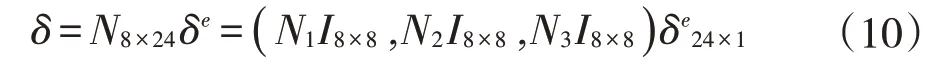
式中：I8×8为单位方阵。

单元内截面ζ上任意点应变ε和应力σ的矩阵形式为

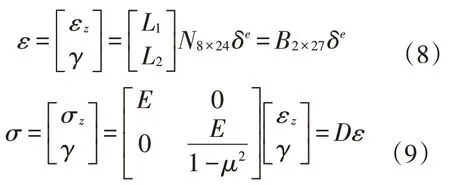
式中：E——材料弹性模量；

μ——泊松比。

因篇幅所限L1、L2的具体表达式不再列出。

基于最小势能原理得到单元刚度矩阵的一般表达式

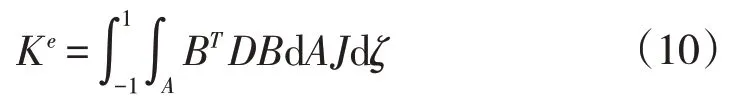
3.3 单元质量矩阵

关于时间t一阶求导的速度空间表达式

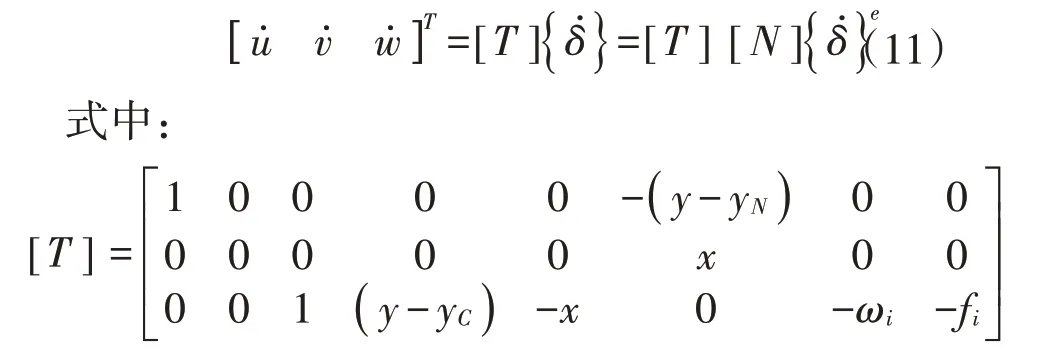
等参梁单元的动能表达式

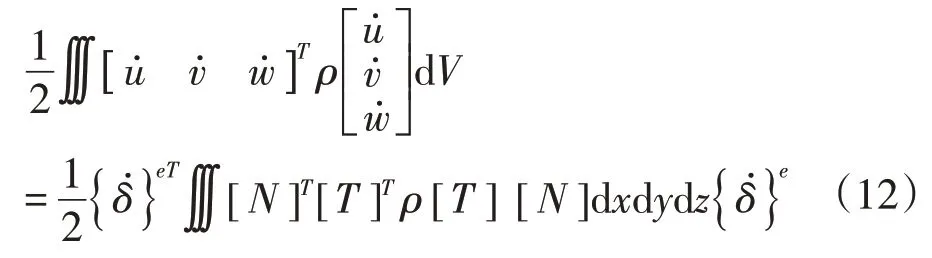
式中：ρ——物质材料的密度。

单元质量矩阵的积分表达形式

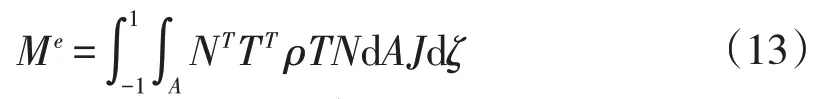
自由振动时，结构的频率方程

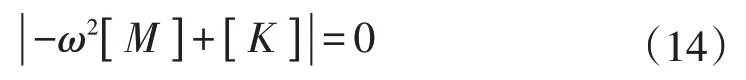
求解式（14）得到结构的自振特性，即求结构质量矩阵、刚度矩阵的广义特征值。

4 参数敏感性分析

现选取某市一座三跨变截面钢-混组合连续梁桥[10]，采用MIDAS/CIVIL 建立整桥模型。通过对比MIDAS CIVIL(MMC)、不考虑剪力滞效应（MI）的计算方法和考虑剪力滞效应（MSL）的算方法所得数值结果，分析梁高变化形式、混凝土强度、腹板斜率、翼宽比、宽跨比等因素对组合箱梁固有频率的敏感性。

4.1 梁高变化形式

变截面箱梁高度的变化常通过指数函数的幂次方变化来实现，采用1.3、1.5、1.8、2.0、2.2 次方。随着幂次方的增大，变截面连续箱梁桥各固有频率均逐渐减小，考虑剪力滞效应的固有频率比不考虑剪力滞效应的固有频率小。见表1。

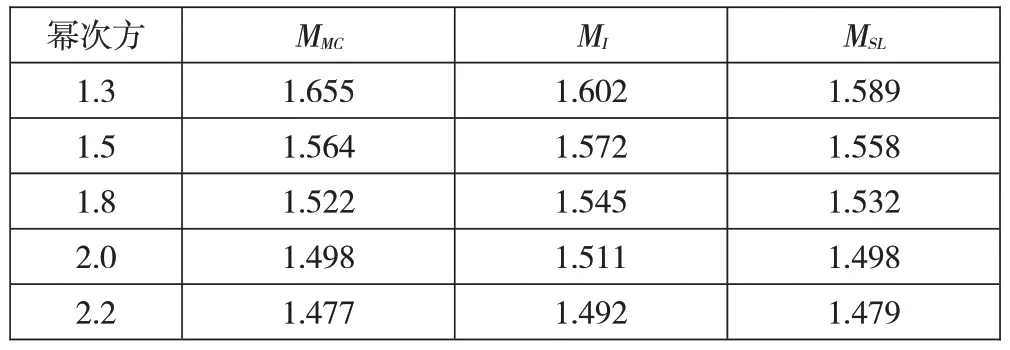
表1 不同幂次方数的固有频率 Hz

4.2 混凝土强度

选取C40～C80的混凝土强度等级，分析混凝土强度对剪力滞效应的敏感性。随着混凝土强度等级的增大，变截面连续箱梁桥各固有频率逐渐增大，考虑剪力滞效应的固有频率比不考虑剪力滞效应的固有频率小。见表2。

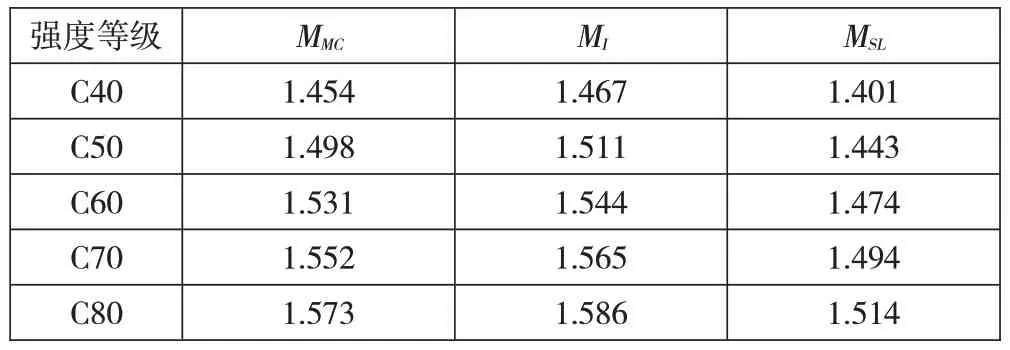
表2 不同混凝土强度下的固有频率 Hz

4.3 腹板斜率

为研究不同腹板倾斜度下箱梁的剪力滞效应，倾斜角α分别选取为70°、75°、80°、85°、90°。随着腹板倾斜角的增大，变截面连续箱梁桥各固有频率逐渐增大，考虑剪力滞效应的固有频率比不考虑剪力滞效应的固有频率小。见表3。

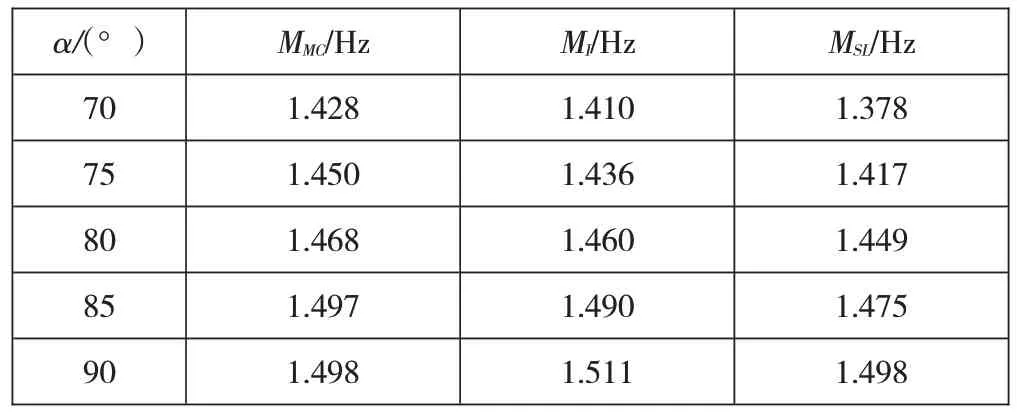
表3 不同腹板斜率的固有频率

4.4 翼宽比

翼宽比为bp与bt之比，取 0.2、0.4、0.6、0.8、1.0。随着翼宽比的增大，变截面连续箱梁桥各固有频率逐渐减小，考虑剪力滞效应的固有频率比不考虑剪力滞效应的固有频率小。见表4。

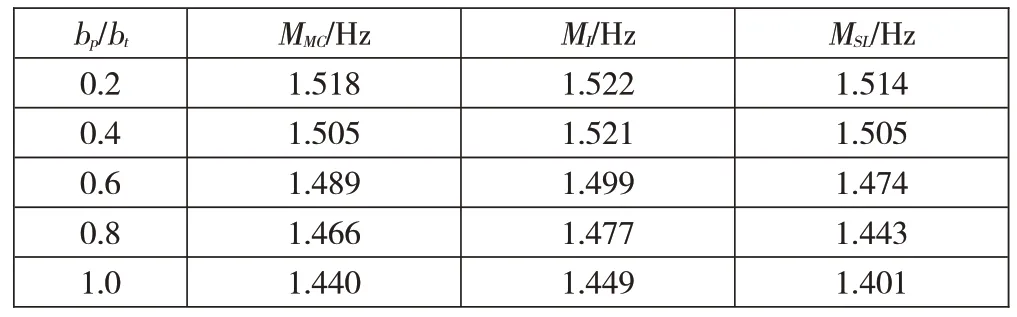
表4 不同翼宽比的固有频率

4.5 宽跨比

宽跨比为bt与中跨跨长L之比，边/中跨比保持不变，宽跨比分别选取 0.100、0.075、0.060、0.050、0.040。随着宽跨比的增大，变截面连续箱梁桥各固有频率显著增大，考虑剪力滞效应的固有频率比不考虑剪力滞效应的固有频率小。见表5。

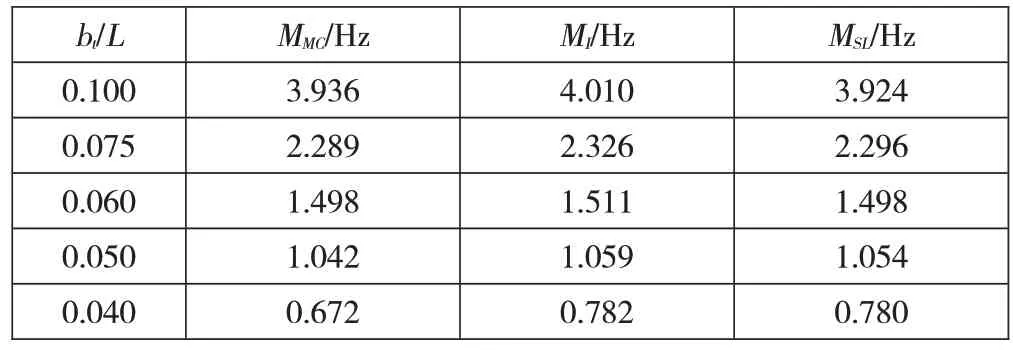
表5 不同宽跨比的固有频率

5 结论

1）提出一种用于变截面连续箱梁能够考虑剪力滞效应计算分析的三节点梁段法，基于最小势能原理推导了等参有限元行列式并编写了有限元计算程序。算例模型的数值结果与实测值吻合良好，验证了理论公式推导和程序编写的正确性和实用性。

2）通过工程实例研究了变截面连续箱梁，在是否考虑剪力滞效应的情况下，其固有频率随梁高变化的幂次方数、混凝土强度、腹板斜率、翼宽比和宽跨比等因素变化的规律。

3）工程实例中，宽跨比不仅是变截面连续箱梁桥剪力滞效应分析的主要影响因素，而且宽跨比的变化对变截面连续箱梁桥固有频率的敏感性影响十分显著。

4）分析结果表明，变截面连续箱梁桥的固有频率因考虑剪力滞效应而减小。验证了剪力滞效应削弱结构刚度的现象且在箱梁桥设计与计算时应给予充分的重视。