横向振荡柱体尾流P+S模式及其演化研究

郑之明，邵传平

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

流体流经钝体时，旋涡以一定的频率在钝体的表面形成后脱落，比如风吹过输电桩、高楼，水流经过桥墩、海洋中的石油立管。旋涡的交替脱落会使柱体表面的压力分布发生周期性的变化，由此带来的交变载荷会引起圆柱振动[1]，带来安全隐患，特别是当这个交变载荷的变化频率与圆柱的固有频率接近时会引发共振，使柱体的振幅急剧增大，以致造成破坏性的后果[2]。前人对涡激振动的研究主要集中在流动条件(雷诺数)、几何条件(柱体长径比)、端部约束条件(悬臂、简支、弹性支撑等)和材质条件(刚度、阻尼比及流固质量比)[3-6]，MOE[7]、KHALAK[8]和SINGH[9]等对旋涡脱落模式进行了研究，发现涡脱模式与流速、振幅、壁面粗糙度和振动频率等因素关系密切。

系统地研究参数众多的涡激振动十分困难，故进行合理的简化处理非常必要。由于工程中常见的涡激振动振幅和振频变化很小，因此可以单独研究某个截面的振动[10]，以二维振动柱体的振幅、振频及来流速度代替此截面上的对应参数，可以大大降低研究难度，便于定量研究。强迫振荡柱体绕流可以分为横向振荡柱体绕流和流向振荡柱体绕流。ONGOREN和ROCKWELL[11]的研究表明一般斜向振荡柱体尾流的各种旋涡脱落模式都在横向和流向振荡柱体尾流中出现。WILLIAMSON等[12]根据大量数据定义了尾迹旋涡脱落模式，最简单最基础的为单个涡街S(single)和一对涡街P(pairs)，对应复杂的旋涡脱落为2S、P+S、2P、2C和2T尾流模式。本文研究其中的P+S模式。

为了控制柱体尾流中的旋涡脱落以及减小阻力，发展出了一些控制方法[5,14-16]，其中添加窄条控制件有着简便、无需引入外部能量的优势，窄条控制件的宽度和控制件相对振荡柱体的位置影响着控制效果。本文通过风洞实验和数值模拟研究在横向振荡柱体下游添加窄条控制件对大振幅工况下P+S涡脱落模式的控制效果。

1 模型及实验方法

试验在中国计量大学回流式风洞实验室中进行，风洞实验段长2.0 m，横截面积0.6 m×0.6 m，可提供速度0.6～30 m/s，湍流度小于0.5%的均匀来流。风洞的壁面为有机玻璃，靠电机一侧开有一个长10 cm宽6 cm的矩形孔，振荡柱体从这里伸入，振荡柱体为长度100 cm，直径D=2.5 cm，壁厚0.8 cm的铝管。铝管一端伸入风洞，另一端和驱动装置连接。驱动装置由连杆与转轮组成，由电机驱动，通过改变电机的转速可以控制柱体的振荡频率，转轮上有特制的孔用于与连杆连接，连接不同的孔可以改变柱体的振幅。

模型与实验布置如图1。窄条控制件在柱体下游尾迹中心线两侧对称放置，其厚度为0.8 cm，宽度为b=0.8 cm，长度为60 cm，材料为铝合金。速度采集使用DANTECT公司生产的恒温热线风速仪，其测量速度范围为0.02～300 m/s，可测量波动频率达300 kHz。热线风速仪的探头均匀分布在X/D=6，Y/D=0～±3.2处，间隔为1 cm，共17个点。本次实验的采样频率为256 Hz，采样时间是20 s，这样在每个测量点会测得5 120个数据。

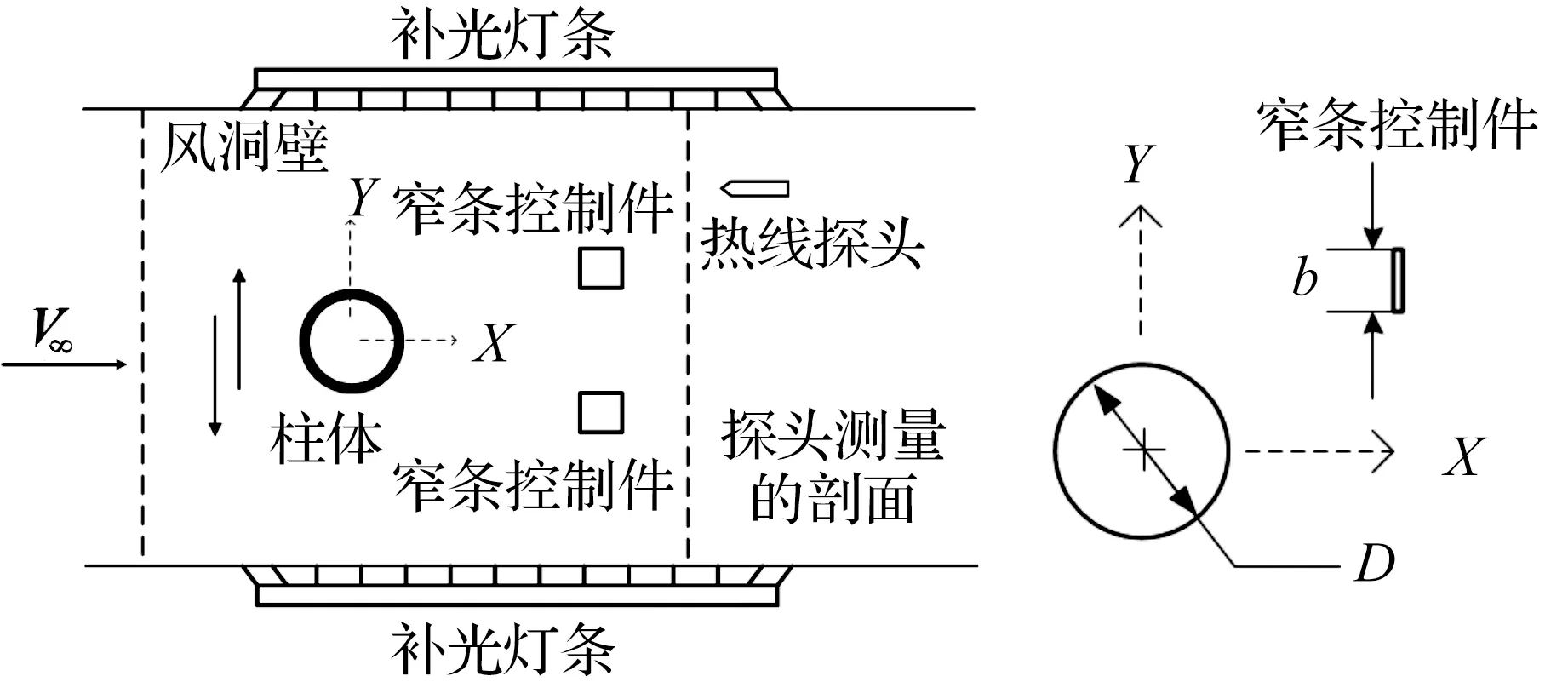
图1 模型与实验布置Figure 1 Model and experiment arrangement

为了观察旋涡脱落模态需要进行烟线显示实验。实验时在柱体上游一定位置处放置一条直径40 μm的钼丝，将钼丝两端与烟线发生器的正负极相连，在钼丝上涂以纯度90 %以上的工业甘油，充电后通过烟线发生器的放电按钮使钼丝通电，这时甘油挥发出的烟幕可以显示旋涡脱落的形态，此时使用Photron公司的FASTCAM Mini UX50型高速摄像机以1000 frame/s的速度进行图片拍摄，整个旋涡的变化情况都会被记录下来。

2 数值模拟方法

对于不可压缩粘性牛顿流体的Navier-Stokes方程，二维直角坐标系下，连续性方程，动量方程分别为：

(1)

(2)

(3)

式(1)中：u、v分别为x、y方向的速度分量，m/s；式(2)(3)中：p为压力，Pa；υ为流体的运动粘性系数，m2/s；ρ为流体的密度，kg/s。

运用Workbench画出模型，经过ICEM划分网格，最后导入FLUENT进行计算求解。使用的非结构化网格如图2。计算区域为：上、下两侧距柱体中心的距离为12D，入口和出口距离柱体中心距离分别为20D和60D。振荡柱体周围设置成加密区域，上下两侧距离柱体中心距离为6D，左右两侧距离柱体中心为12D和36D，加密区域与外侧区域通过滑移面(interface)进行分隔和数据交换，通过UDF定义柱体的受迫振荡运动形式。柱体的运动轨迹为

y=Asin(2πfet)。

(4)

式(4)中：A为柱体简谐运动的振幅，cm；fe为振频，Hz；t为时间，s。

图2 所采用的非结构网格Figure 2 Unstructured mesh used in the simulation

采用RNG k-ε湍流模型，上下边界设置为无滑移固定墙(No Slip Stationary Wall)。振荡柱体和控制板设置成刚体。入口条件为速度入口(velocity-inlet)，速度为v∞=0.7 m/s，出口为自由流出(outflow)。压力速度耦合及SIMPLE格式求解N-S方程。时间导数项为二阶隐格式(Second Order Implicit)，空间离散：扩散项(梯度项，Gradient)用基于单元体的最小二乘(Least Square Cell Based)方法进行插值；对流项(动量项，Momentum)采用二阶迎风格式提高解的准确度，压力项采用二阶精度离散。流体介质为空气，实验室温度为15℃，空气密度为ρ=1.225 kg/s，运动黏性系数为v=14.4×10-6m2/s。

为验证网格无关性，选择5种不同密度的网格，对雷诺数Re=855的均匀流绕静止柱体的流动进行验证。表1展示了5种网格对应的阻力系数CD和斯特罗哈尔数St的计算结果。随着网格数的增加，到网格4时St达到0.250 3，CD达到1.467 3，之后再增加网格数目St和CD变化缓慢。网格5比网格4网格数增加了43.6%，但是St相差仅为0.08%，CD相差仅为0.127%。表2对比了其他研究者的数据，综合考虑决定使用网格4进行仿真计算。

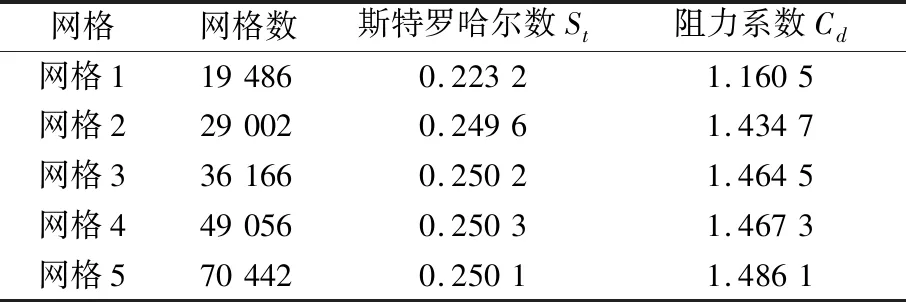
表1 网格密度对Re=855静止圆柱绕流数值计算结果的影响Table 1 Influence of the mesh density on the numerical results of flow across a stationary cylinder at Re=855

表2 Re=855时本文静止圆柱绕流数值结果与其他作者研究结果的比较Table 2 Comparisons of present numerical work with other authors' results for the flow across a stationary cylinder at Re=855

3 结果与分析

当雷诺数为1 200，柱体振幅比A/D为1.5，无量纲振荡频率feD/V∞为0.2(A为振幅，D为圆柱直径，fe为柱体强迫振荡频率，V∞为来流速度)，这时的旋涡脱落为明显的P+S模式，即在每个振荡周期内圆柱一侧释放出单个旋涡，在另一侧释放出一个旋转方向相反的对涡。

3.1 控制件对旋涡脱落模式的改变

图3(a)(b)分别为烟线流动显示的图片和数值模拟的涡量场，实验和仿真的对比情况良好，上侧为一顺时针旋转的单涡，下侧为一对旋转方向相反的对涡。

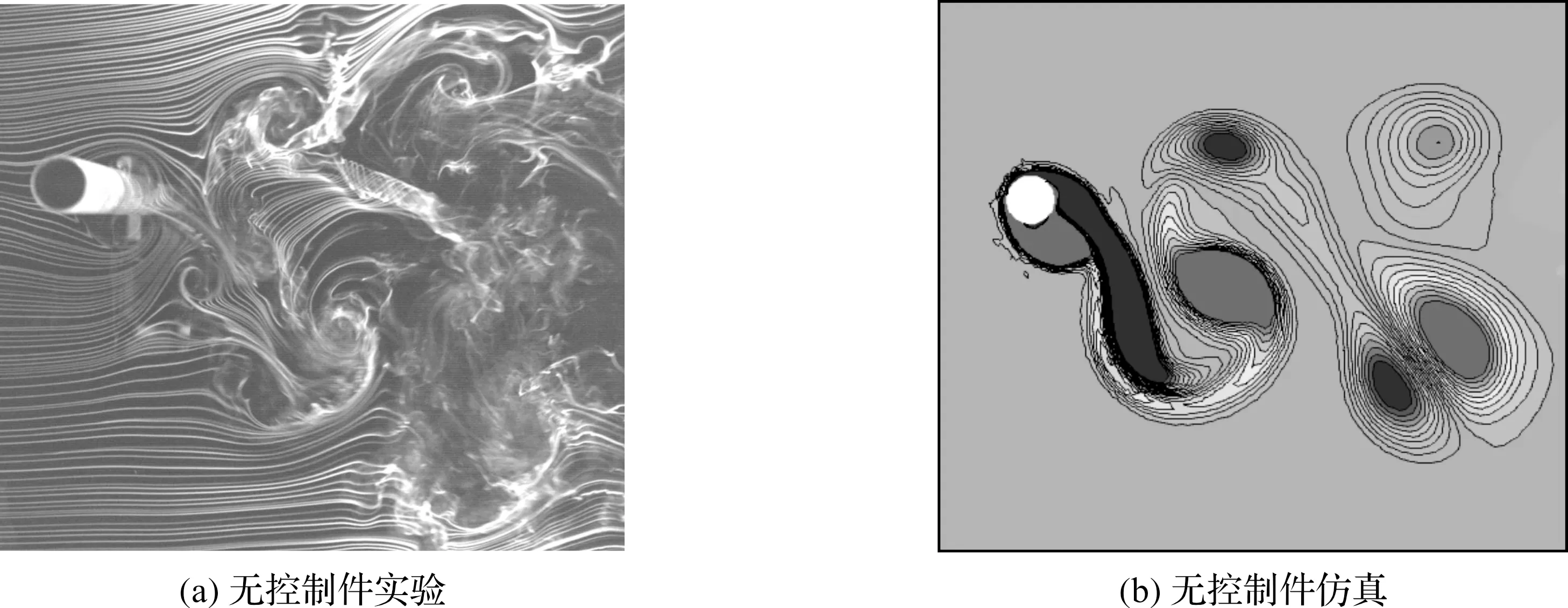
图3 无控制件时实验和仿真的旋涡脱落模式图Figure 3 Mode of vortex shedding in experiment and simulation without control

如图4，当控制件位于X/D=3.0，Y/D=±0.8位置时，旋涡脱落依旧为P+S模式，上侧为一对旋转方向相反的对涡，其中靠尾迹中心线一侧的涡顺时针旋转，另一侧的涡逆时针旋转。下侧为一逆时针旋转的单涡。此时窄条控制件与柱体距离较远，控制件对振荡柱体的影响很小。

图4 控制件位于X/D=3.0，Y/D=±0.8时实验与仿真比对图Figure 4 Comparisons between experimental and numerical when strip controllers placed at X/D=3, Y/D=±0.8

如图5，当控制件位于X/D=2.4，Y/D=±0.8位置时以及图6控制件位于X/D=2.0，Y/D=±4.4时，原来为P+S模式变为2P模式，即在柱体的一个振荡周期内，上侧为一对旋转方向相反的对涡，下侧同样为一对旋转方向相反的对涡。

如图7，当控制件位于X/D=2.0，Y/D=±1.2位置时，原来为P+S模式变为T+S模式，即在柱体的一个振荡周期内，上侧为三个涡，下侧为一个单涡。

3.2 窄条控制件的作用

窄条控制件对旋涡脱落的影响有4个方面：1)由于横向剪切流在大幅横向振荡柱体尾流旋涡脱落的形成过程中起到重要作用，而控制件对剪切流的阻挡和分流，可以有效地改变剪切流的宽度及其流动方向，从而影响旋涡的形成；2)控制件表面的摩擦力会改变剪切流的强度；3)控制件背压吸力，对柱体脱落涡走向有影响；4)控制件尾流对柱体脱落涡的湍流耗散。

为了定量研究控制件对涡脱强度的抑制效果，对17个监测点的脉动进行谱分析，然后取17个点的平均谱作为评判标准。图8(a)(b)为无控制件实验和数值模拟的脉动速度功率谱，每个谱上都存在几个尖峰，其中与振荡频率相同点的尖峰最高，代表旋涡的特征强度。在X/D=0.4，Y/D=±1.2放置控制件后，实验和数值模拟的功率谱分别为图8(c)(d)。第一尖峰均比无控制件时有明显减小，其他尖峰也有较大幅度减小。

图5 控制件位于X/D=2.4，Y/D=±0.8时实验与仿真比对图Figure 5 Comparisons between experimental and numerical when strip controllers placed at X/D=2.4, Y/D=±0.8

图6 控制件位于X/D=2.0，Y/D=±4.4时实验与仿真比对图Figure 6 Comparisons between experimental and numerical when strip controllers placed at X/D=2.0, Y/D=±4.4

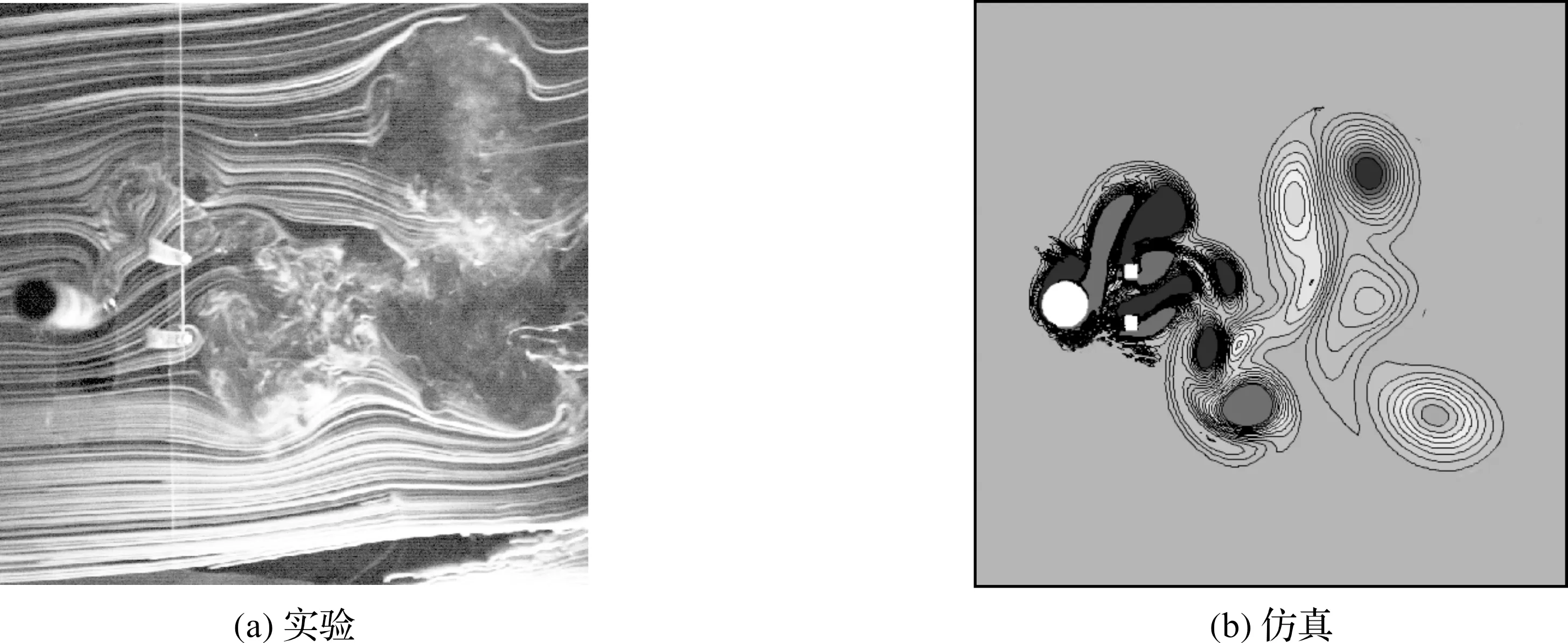
图7 控制件位于X/D=2.0，Y/D=±1.2时实验与仿真比对图Figure 7 Comparisons between experimental and numerical when strip controllers placed at X/D=2.0, Y/D=±1.2

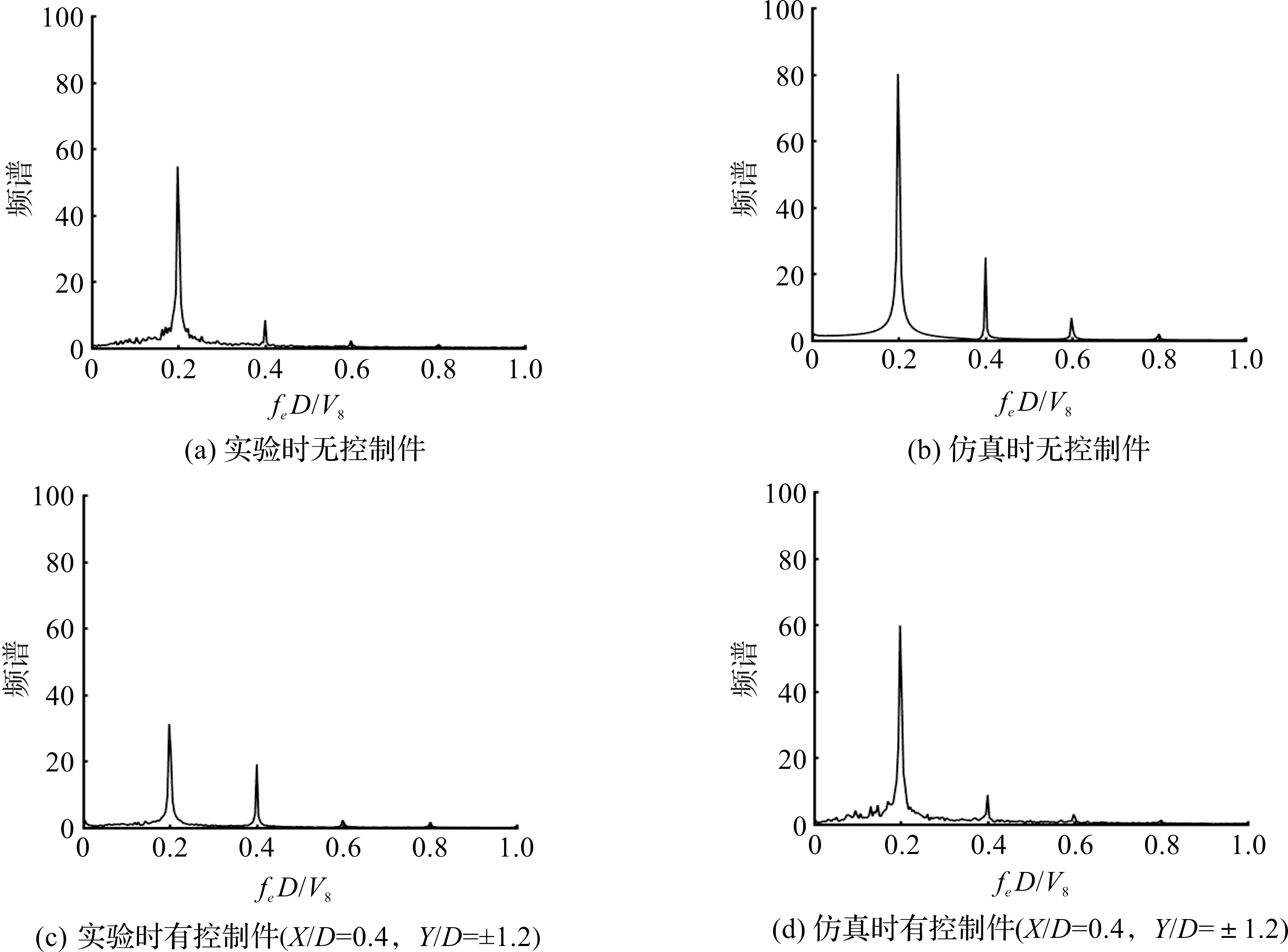
图8 均值频谱对比图Figure 8 Comparison of mean power spectrum

图9为速度分布图，横坐标为各监控点距离y与柱体直径D之比，纵坐标为监控点平均速度u与来流速度v∞之比，当两个控制件之间的距离为Y/D=0.8，控制件与柱体的距离分别为X/D=1.6和X/D=3.2时，大部分监控点的速度较无控制件时要小，说明控制件的抑制效果较好。当增加两个控制件之间的距离时，大部分监控点速度变大，控制件的抑制效果下降。

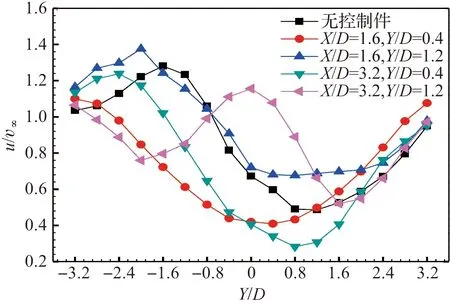
图9 各监控点速度与来流速度之比Figure 9 Ratio of the velocity of each monitoring point to the incoming velocity

4 结 语

在雷诺数Re=1 200，柱体振幅比A/D=1.5，振荡频率feD/V∞=0.2时找到了P+S旋涡脱落模式，并用相对宽度b/D=0.32的窄条控制件进行干扰，实验和仿真的对比情况良好，控制件在一定位置可以明显地改变涡脱模式：当控制件在X/D=2.4，Y/D=±0.8和X/D=2，Y/D=±4时旋涡脱落模式由P+S变成了2P，在X/D=2，Y/D=±1.2时旋涡脱落模式由P+S变成了T+S，证明控制件可以对旋涡生成产生干扰。热线频谱图和速度剖面图说明控制件在一定位置可以成功抑制旋涡脱落强度。此项研究有利于进一步探索涡激振动的破坏来源及应对方案，对研究各种模式之间相互转化的机理亦有一定的参考价值。工程应用方面对海洋立管、桥墩和高楼等有强烈水流或气流经过的设施或建筑物的建设保护也有着一定指导作用。