两轮自平衡车CMG永磁电机控制系统

肖 曦 唐艺伟 张 猛

（1.清华大学 电力系统及发电设备安全控制和仿真国家重点实验室 北京 100084；2.北京控制工程研究所 北京 100080）

引言

两轮自平衡车是智能车辆的一个分支，拥有体积小巧、机动性高、驾驶简单、适用性广等特点，已经吸引了许多技术企业和投资者的关注。美国的LitMotors公司在2013年首先提出了两轮自平衡概念车型C-1，此车型采用陀螺稳定器技术，通过一组控制力矩陀螺（control moment gyroscope， CMG）使得车身本体保持姿态平衡[1]。国内的凌云智能公司也从事两轮自平衡智能电动车开发[2]，其于2015年7月获得1 000万美元A轮投资，现已推出第三代样车。日本的雅马哈公司于2017年推出名为MOTOROiD的概念车型，成为同年东京摩托车展上的一个焦点。

考虑到力矩输出能力和电气控制难度，现有的两轮自平衡车多基于单框架CMG系统实现。CMG系统由陀螺电机和框架电机组成，其中陀螺电机高速旋转、提供角动量量值；框架电机带动陀螺电机旋转、提供角动量方向变化；二者配合产生内部力矩抵消外界的倾覆力矩。两个CMG系统前后对称安装，实现自平衡车偏航和侧倾的解耦，如图1所示。

取图1中的坐标系约定，记陀螺电机角动量量值为H，两个框架电机旋转角度分别为±φ，列写车身绕x轴的角动量定理方程可得两个CMG系统产生的内部力矩L为：

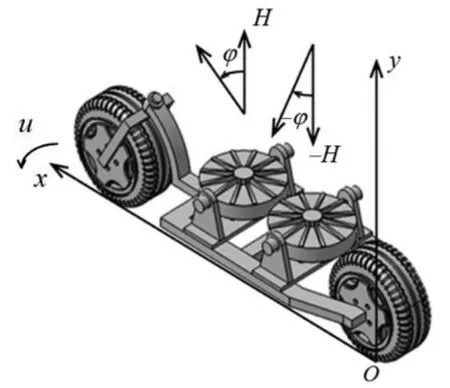
图1 两轮自平衡车原理示意图

电机选型和电机控制是CMG系统的重要任务，永磁同步电机结构简单、功率密度高、效率高、控制性能好，被广泛应用于高精度伺服系统、舰船推进系统、牵引系统、节能控速系统等多个领域中[3]。通过合理地设计永磁体结构并相应地布置电枢绕组，可以在每相绕组中获得正弦波或梯形波的反电动势。为了区分此两种电机，具有正弦波相反电动势的永磁同步电机被称为永磁交流电机（permanentACmachine，PMACM），具有梯形波相反电动势的永磁同步电机被称为无刷直流电机（brushlessDCmachine，BLDCM）。

为保证角动量量值大而稳定，CMG系统要求陀螺电机恒定高速旋转。此外，供电功率确定后，CMG系统还要求陀螺电机尽可能轻便。由于转子转动惯量较大、工作转速较高，转矩波动对电机转速的负面影响较小，因而CMG系统能够容忍陀螺电机拥有较明显的转矩波动。无刷直流电机结构紧凑、控制简单、可靠性强，尤其适用于此种场合。考虑到应用特点并结合设计经验，选取外转子结构的无刷直流电机作为陀螺电机，并在轴系上附加飞轮体以满足惯量要求。为保证输出力矩灵活可控，CMG系统要求框架电机拥有较好的速度伺服性能。此外由于安装空间限制，框架电机也应该有较高的功率密度。考虑到框架电机的运行速度较低，运行负载较大，适合使用永磁同步电机直驱运行。

1 CMG系统无刷直流电机控制

1.1 模型建立

采用三相六状态导通制，假设电机内部物理过程及驱动电路换向过程完全理想，可得到无刷直流电机的数学模型如下：

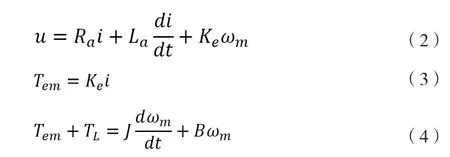
式中：

u—导通两相的端电压；

i—流经电流；

Ra—总电阻；

La—有效电感；

Ke—电机反电动势系数；

ωm—机械转速；

Tem—电磁转矩；

TL—负载转矩；

J—轴系转动惯量；

B—轴系阻尼系数。

由于CMG系统中陀螺电机并不带载，此处负载转矩TL仅用于代表阻尼力矩的非线性部分。

1.2 控制器设计

用作CMG系统陀螺电机时，受控无刷直流电机的机械时间常数将远大于电磁时间常数，因而可使用级联式结构，将控制任务分解至速度环和电流环双环，得到如图2所示的电机控制框图。

首先讨论电流环的控制器设计。电流环主要呈现一阶特性，因而可使用PI控制器进行控制，记控制器传递函数为：

将逆变器建模为一个小延时环节，即：

其中Tinv取为PWM周期的一半[4]。为将反电动势纳入考虑，通过结构图变换得到图3所示的电流环控制框图，同时得到电流环的开环传递函数为：

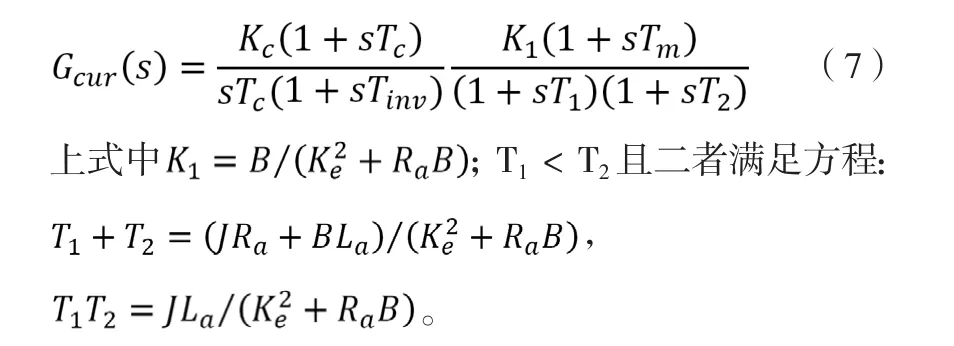
作近似1+sTm≈sTm，同时选取

此时电流环开环传递函数形如典型二阶系统，选取

完成电流环控制器参数整定后，讨论转速环控制器的设计。由于机械时间常数远大于电磁时间常数，因而可对电流环进行一阶近似，此时电流环的闭环传递函数为：

式中：

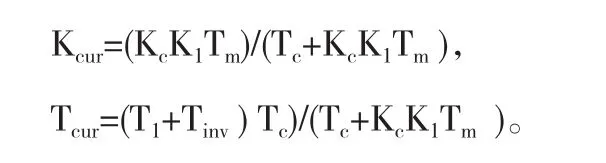
转速环的结构如图4所示，其开环传递函数可以近似为：

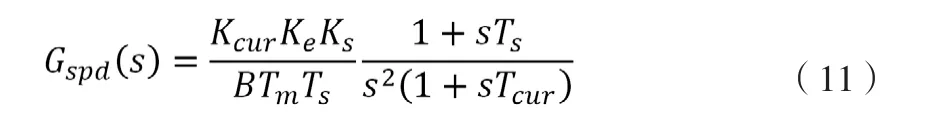
相应地，其闭环传递函数形式为：

上式中各参数分别为a0=(KcurKeKs)/(BTmTs)，a1=(KcurKeKs)/BTm，a2=1，a3=Tcur。整定参数时，以闭环传递函数幅频响应的“平坦程度”作为优化目标[4]。具体而言，对|Gspd，c(jω) |在ω=0处作泰勒展开，令ω2项和ω4项的系数为零，可得，。从中解出Ks和Ts，完成控制器参数整定。

1.3 控制器离散实现

PI控制器形式简单，在连续控制器的基础上使用离散求和代替积分即可得到离散形式的控制器。当采样周期远小于闭环系统最小的时间尺度时，离散化引起的误差可以忽略不计。仿真或实验中可进一步调整参数以适应不同的性能需求。

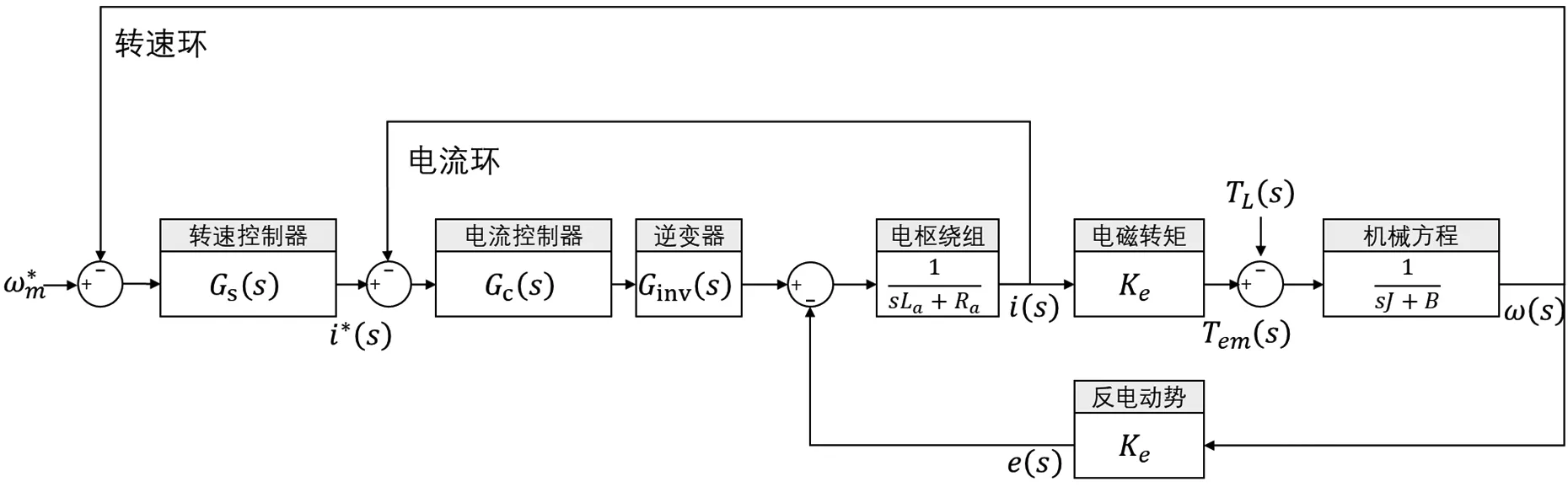
图2 无刷直流电机控制框图

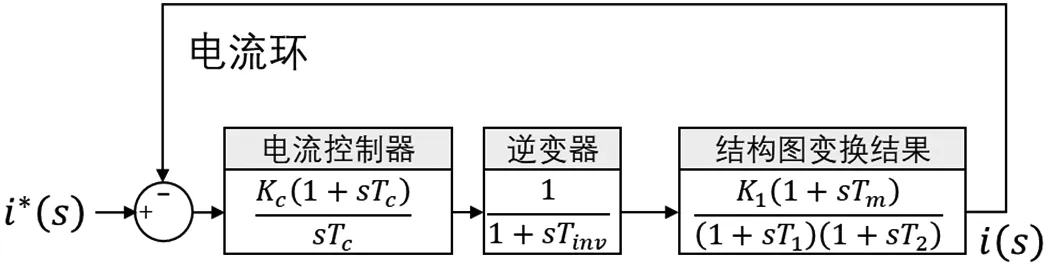
图3 无刷直流电机电流环控制框图

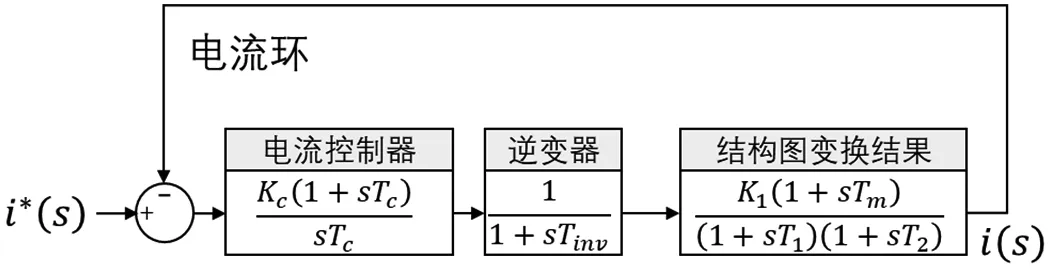
图4 无刷直流电机转速环控制框图

2 CMG系统永磁交流电机控制

2.1 模型建立

理想永磁交流电机的数学模型为：

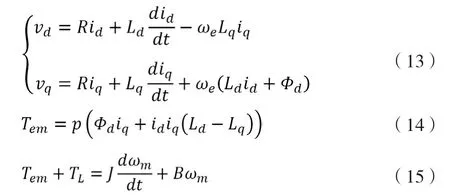
式中：

vd，vq—d轴q轴的电压；

id，iq—d轴q轴的电流；

R—电枢电阻；

Ld—d轴电感；

Lq—q轴电感；

Φd—d轴永磁体磁链，

p—电机极对数；

ωe—电机电角速度；

ωm—机械角速度；

Tem—电磁转矩；

TL—负载转矩；

J—轴系转动惯量；

B—轴系阻尼系数。

用作CMG系统框架电机时，受控永磁交流电机的工作转速相对于其额定功率下的转速较低，因而dq轴反电动势量值较小，对解耦策略要求不高，通常前馈解耦即可满足要求。假设d、q轴完全解耦，d轴电流被控制为0，则有：

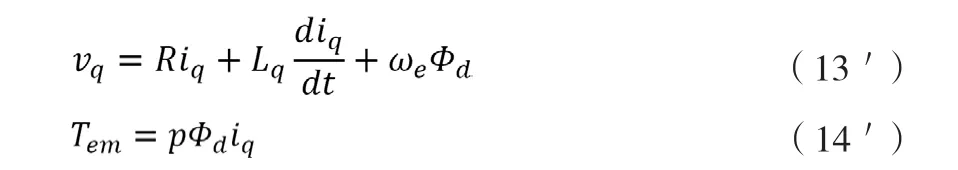
（13＇）（14＇）（15）三个方程形式上与（2）至（4）三个方程类似。

CMG系统中框架电机带动陀螺电机旋转，其机械方程中除J表征的惯量项及B表征的阻尼项之外，还有额外的负载力矩即环架扭矩(gimbal torque)，记作TL1。为分析环架扭矩的形式，考虑固定于车身的非惯性系。在此系中，陀螺电机受离心力、欧拉力和科里奥利力三种惯性力。假设陀螺电机完全对称，其安装在框架电机轴系上时无偏心、无倾斜，则离心力和欧拉力不产生净力矩，环架扭矩完全由科里奥利力产生，简单矢量计算可得：

上式中u为车身侧倾角速度，H为陀螺电机角动量，φ为框架电机旋转角度。对框架电机施以控制时，车身侧倾角速度大小未知，因而TL1应视为外界负载扰动。

负载力矩中未被TL1建模的部分统一记作TL2，这包括阻尼力矩的非线性项、机械安装非理想性导致的耦合力矩等，这部分同样也是未知的。由定义TL=TL1+TL2。

2.2 控制器设计

由于受控永磁交流电机的机械时间常数同样远大于电磁时间常数，因而可使用级联式结构，将控制任务分解至速度环和电流环双环。

就电流环而言，由于运行速度较低，dq轴耦合不严重，作前馈解耦后永磁交流电机的电流环控制任务类似于无刷直流电机时的情形，可采用相同的控制器设计方案和参数整定方法。电流环控制器设计完成后，取闭环电流环的一阶近似，即：

转速环的情形有所不同，一方面，用作CMG系统框架电机的永磁交流电机需要有良好的速度伺服性能；另一方面负载力矩组分复杂、难以测量，对速度性能影响较大。传统的级联PI控制器难以同时兼顾动态响应速度和抗扰能力，一种解决思路是设计二自由度控制器，如文献[5][6]；另一种思路是利用转速信息对负载转矩进行观测，并使用观测值进行前馈补偿。实际系统中，为获取电机转速，通常需要对机械传感器采集的数据进行差分，为了减小测量噪声的影响，又需要加入滤波环节，这会向转速测量引入延时，不利于转速环带宽的提高，极端情形下甚至可能导致转速环失稳。若使用位置信息作为反馈值，通过观测器可以同时观测出转速和负载转矩，在提高抗扰能力的同时也能获得低延时高精度的转速测量值，因而尤其适用于CMG应用场合。

扩展状态观测器（extended state observer， ESO）由韩京清等人提出[7]，Guo给出了一般情况下的收敛性证明[8]。此方法的主要思想在于将负载转矩作为系统的“扩展状态”、和转子位置以及转速一起构成“扩展系统”的状态变量，对此扩展系统设计观测器得到转速和负载转矩的观测值。使用扩展状态观测器的永磁交流电机控制框图如图5所示。

对于永磁交流电机，列写扩展系统状态方程有

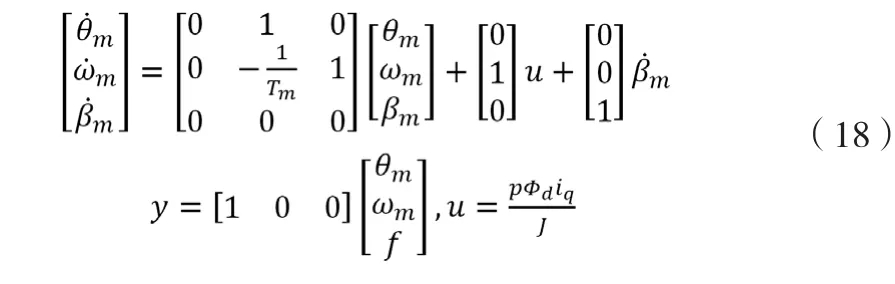
式中：

θm—电机机械角位置；

ωm—机械转速；

βm—负载力矩产生的机械角加速度；

u—电磁转矩产生的机械角加速度；

Tm=J/B—电机时间常数。

（18）式可简记为：

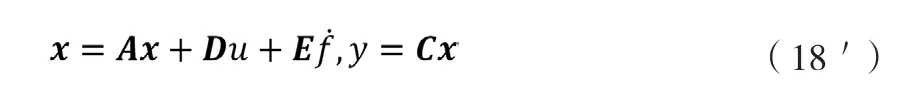
考虑参数误差，选取ESO的系统方程为：

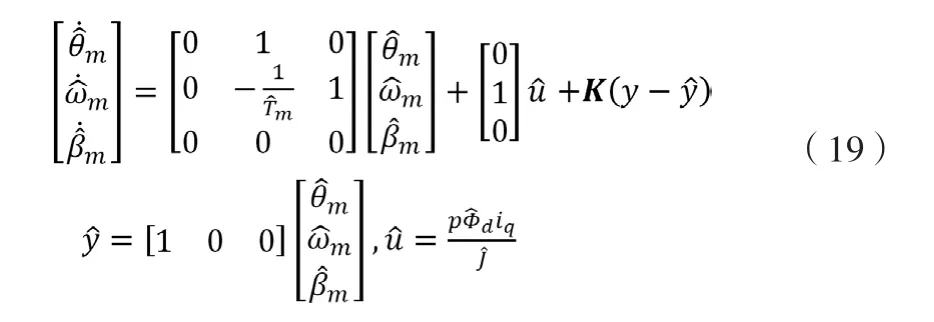
其中带角标的符号表示对真实物理量的观测或估计。（19）式可简记为

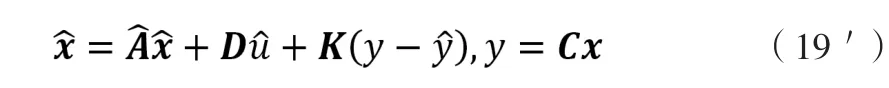
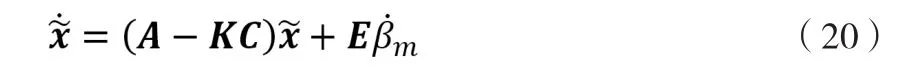
选取K以使得sI-(A-KC)在s=-ω0处拥有三重根。此时

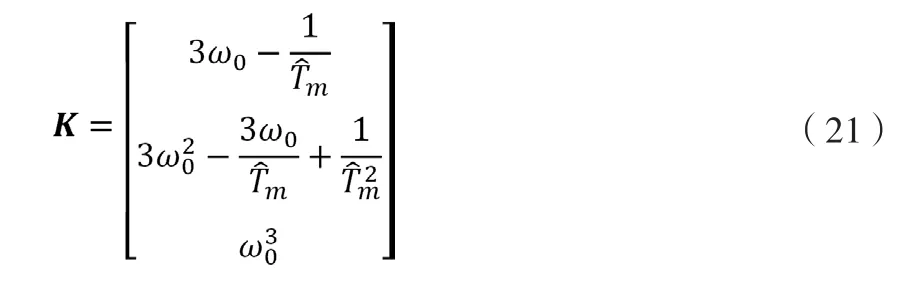
应施加的前馈电流iq，com由观测量直接得到：

2.3 ESO性能与闭环机电特性分析

容易推得自iq和TL至iq，com的传递函数分别为：

现对（23）（24）两式做一定物理解释。首先注意到两个传递函数中均含有来自于ESO的三阶极点s=-ω0。此三阶极点构成一低通环节，频率远小于ω0的输入成分几乎不受此低通环节影响，因此可以认为ω0代表ESO的带宽。此外，两个传递函数中也含有与电机机械常数有关的一阶极点，可以认为ESO使用机械角位置信息得到角加速度信息，从中去除电磁转矩的影响后观测出负载转矩的量值。由于轴系阻尼的存在，iq产生的电磁转矩和TL表示的负载力矩到转速的传递函数必有一由电机机械参数决定的低通环节，此低通环节的影响最终反映在前馈电流中，对应（23）（24）两式分母中的1+sTm项。ESO使用的电机参数的准确性影响两式的零点，假设各电机参数完全准确，则(iq，com(s)/TL(s)发生零极点对消，而(iq，com(s)/iq(s)为零，即iq，com(s)完整反映了负载力矩TL(s)，而不含有iq(s)的影响。若使用的参数不准确，则ESO既无法准确去除电磁转矩的影响，因而(iq，com(s)/iq(s)为零；也无法由转速信息准确得到负载转矩，因而(iq，com(s)/TL(s)存在幅值和相位的扭曲。

容易推得自ωm和TL至的传递函数分别为：

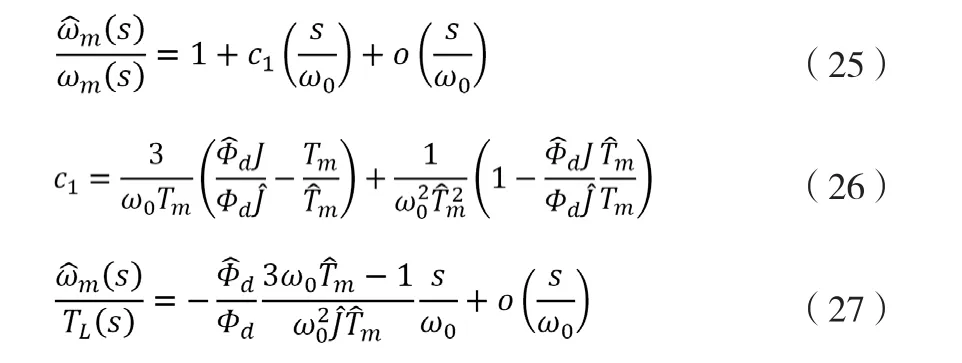
其中o(s/ω0)表示s/ω0的高阶项。可以看出当参数准确时，中s/ω0的一阶项系数c1为零（进一步计算可知此时高阶项也为零），而并无此结果。这意味着即使参数准确，使用估计ωm仍然有误差，此误差源于负载转矩的影响。不过由于无常数项，可知在阶跃形式的负载扰动下，ESO仍能实现对转速无差估计。此外，提高带宽有助于提高观测精度，在转速环关注的频率范围内，可以认为|s/ω0|≤ 1，此时≈ωm。

ESO的性能对闭环机电特性有直接影响。记G1(s)=(iq，com(s)/iq(s)及 G2(s)=(iq，com(s)/TL(s)，在转速环频段内，忽略电流环的sTc项，忽略ESO极点的影响，容易得到自至电流环输出iq以及自TL至iq的传递函数：

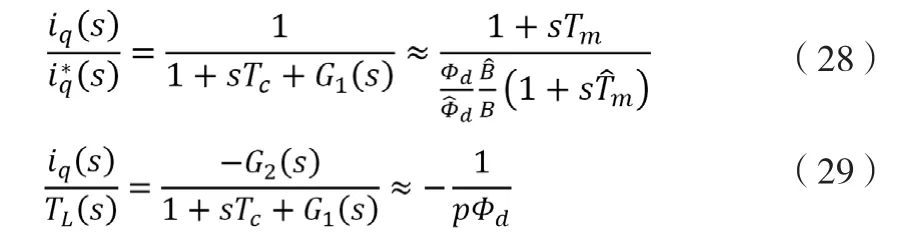
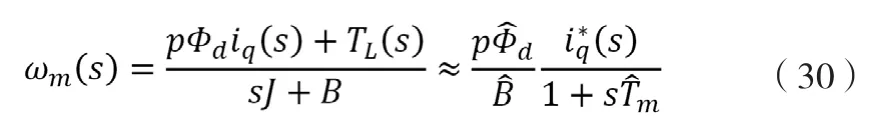
（30）式表明闭环机电特性正如同设计ESO时对系统模型的估计。可以做这样的理解：对这种估计的偏离不管来源于负载力矩还是参数偏差，都会被ESO判定为负载力矩的影响并且加以校正，最终使得闭环机电特性接近最初的估计，即参数偏差对闭环机电特性性能没有负面影响。

为讨论ESO的带宽以及参数偏差对闭环机电特性稳定性的影响，考虑闭环系统穿越频率ωc。假设对电机机械时间常数的估计准确，即。由于机械时间常数较易测量，工程实践中满足此假设并不困难。令1+jωcTc+G1(jωc)=0，容易得到：

其中θ=Tc/Tm为闭环电流环时间常数与电机机械时间常数之比，λ= 1/ω0Tm可表征带宽宽度。随带宽增大，λ减小，增大，即闭环系统对参数偏差的鲁棒性提高。考虑到电流环一阶假设和对离散化的需求，不应把带宽取得过大。令λ=θ，此时，ωc=ω0。其物理意义为：当带宽ω0满足ω0Tc=1时，若对受控永磁交流电机参数J/Φd的估计值若大于真实值的5倍，则引入前馈电流iq，com将使得闭环系统失稳。

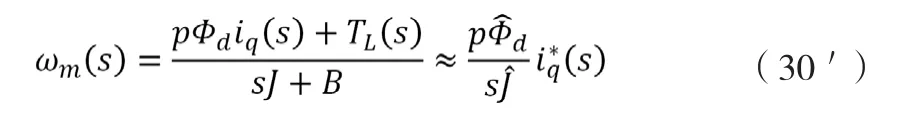
2.4 ESO与卡尔曼滤波器的联系

上述讨论假定电机角位置的测量值完全精确，为说明测量噪声的影响，可以对扩展状态观测器和卡尔曼滤波器作一比较。卡尔曼滤波器同样可被用于观测电机转速[9]以及负载力矩[3]，使用时需假定系统模型完全准确、将负载力矩处理为系统噪声并假定系统噪声和测量噪声均为协方差矩阵已知的白噪声，此时卡尔曼滤波器是最小方差意义下的线性最优滤波器。但明显可见，此种方法对负载力矩的假设偏离实际情况，此外设置协方差矩阵时需要试凑或需要从已有数据中估计，增大了工作量且不利于物理解释。卡尔曼滤波器迭代式地计算最优增益并作状态变量反馈，后者形式上和ESO有相似之处。为了简洁起见，此处讨论连续形式的卡尔曼滤波器，即Kalman-Bucy滤波器。

列写系统方程有：

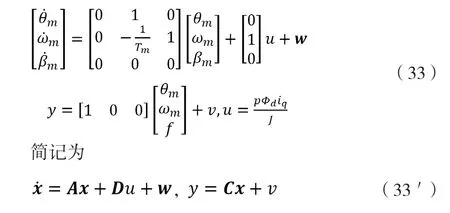
观测器结构及增益计算方式为：

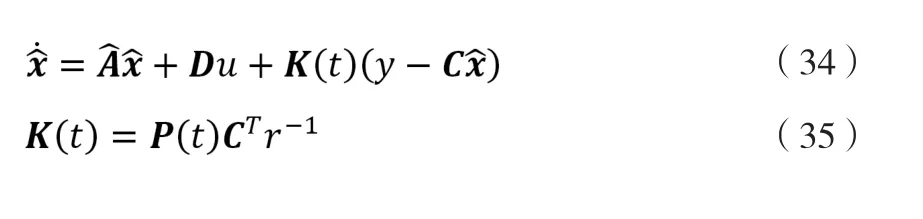
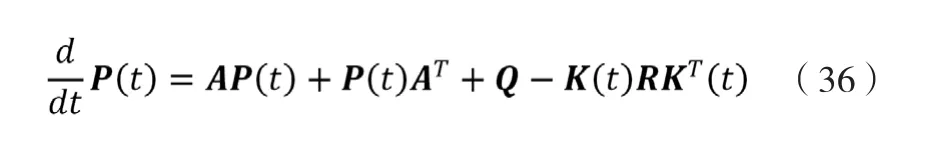
其中r为v的方差，Q为w的协方差矩阵。若只考虑角加速度受系统噪声，则w仅一个非零元素，相应地Q仅在主对角线上有一非零元素。由于反馈增益仅与测量噪声与系统噪声方差之比有关，不失一般性，可取

据文献[10]的结论，可以验证得知（36）式有一与初值无关的极限解P*，由P*得到的反馈增益K*即为观测器稳态反馈增益。定义观测器稳态下的带宽为矩阵特征值模的最小值，可与ESO的带宽相对应。借用对ESO的分析可以知道观测器的性能主要受此带宽影响，作与r的关系如图6所示。由于在百赫兹至千赫兹级别时，与r的关系几乎不受在合理范围内（百毫秒量级以上）变化的影响，此处不再具体说明。

从图6中可以看出：测量噪声方差越小，设计出的卡尔曼滤波器闭环带宽越高。反映在ESO设计过程中可知为了适应测量噪声的影响，可以降低带宽ω0，此时ESO低通环节的滤波作用更为明显。

2.5 控制器离散实现

使用前向欧拉法对（18）式所示的系统状态方程进行离散，得到：

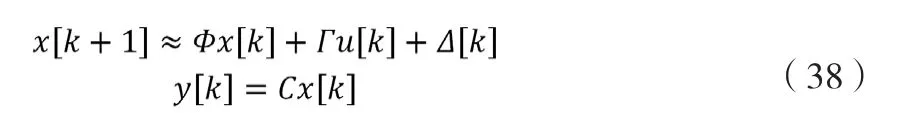
其中

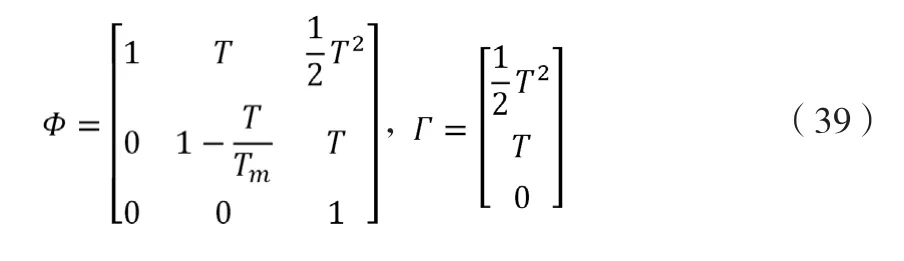
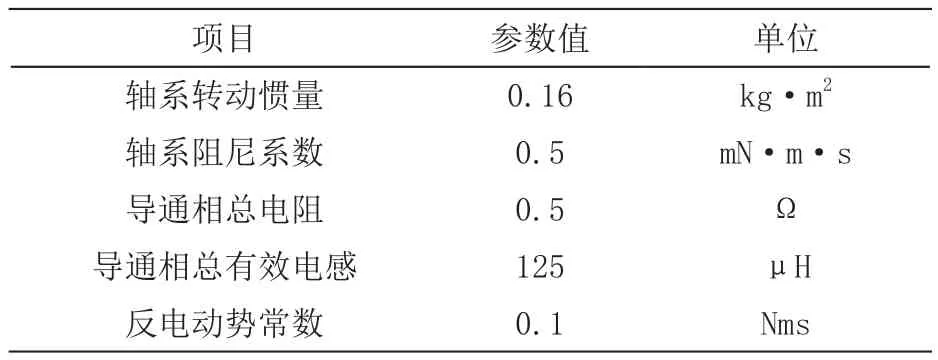
表1 无刷直流电机控制器设计算例参数

考虑如下形式的离散形式观测器系统方程：

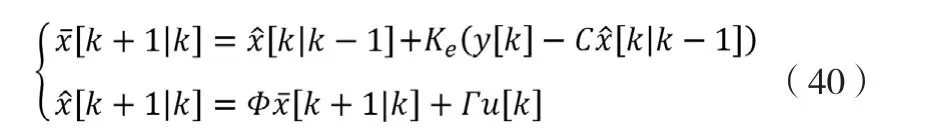
当采样周期Ts和观测器带宽ω0满足Tsω0≤1时，调整Ke以使得Φ-ΦKeC的特征根为1-Tsω0，此时离散化引起的误差很小，可被观测器的闭环结构自行校正。

3 仿真验证

对于无刷直流电机，选取算例参数如表1。取转速参考值为100 rpm，母线电压为72 V，电流极限值为2.5 A。电机空载启动80 s后突加0.1 Nm的恒转矩负载，在SimulinkR2018b里使用变步长混合阶数的龙格库塔方法对系统仿真，得到输出如图7和图8。

由图7和图8可以看出，升速过程中导通电流保持在极限值2.5 A，当转速接近参考值100 rpm时，导通电流快速下降至0.5 A，对应的电磁转矩用于抵消阻尼力矩。施加阶跃负载时，导通电流快速上升，以产生相应的电磁转矩抵消负载力矩，维持转速不变。

算例中机械子系统和电气子系统时间常数相差多个量级，满足于设计控制器时的假设。前述整定方法选取的参数较为激进，使得控制器本身响应非常迅速，影响系统响应时间的主要因素为母线电流的极限值限制。考虑到离散后的鲁棒性问题，可以减小控制器增益而基本不影响整体系统的性能。

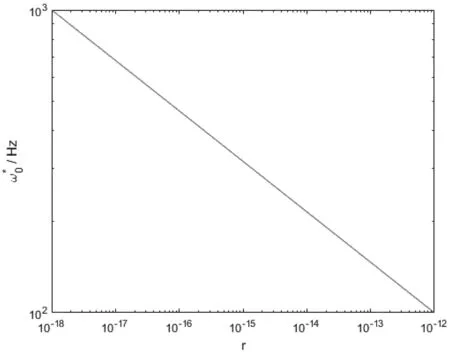
图6 卡尔曼滤波器闭环带宽与测量噪声方差关系

对于永磁交流电机，选取算例参数如表2。令转速指令为幅值50 rad/s频率5 Hz的正弦信号，取无负载扰动、幅值1 Nm的各频率正弦负载扰动、cos t cos φ形式的复杂负载扰动三种情形，比较使用扩展状态观测器前后的系统速度伺服性能，得到图9至图12。

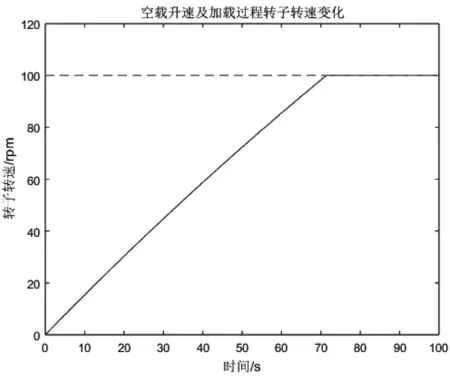
图7 空载升速及加载过程转子转速变化

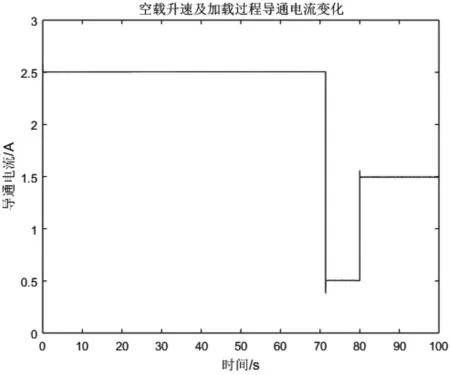
图8 空载升速及加载过程导通电流变化

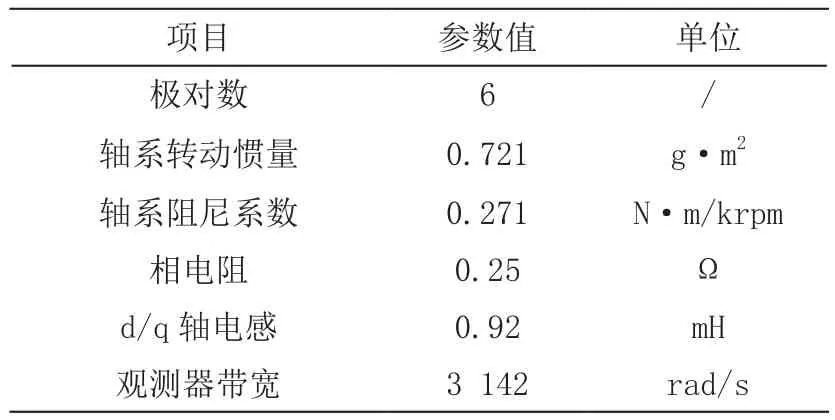
表2 永磁交流电机控制器设计算例参数

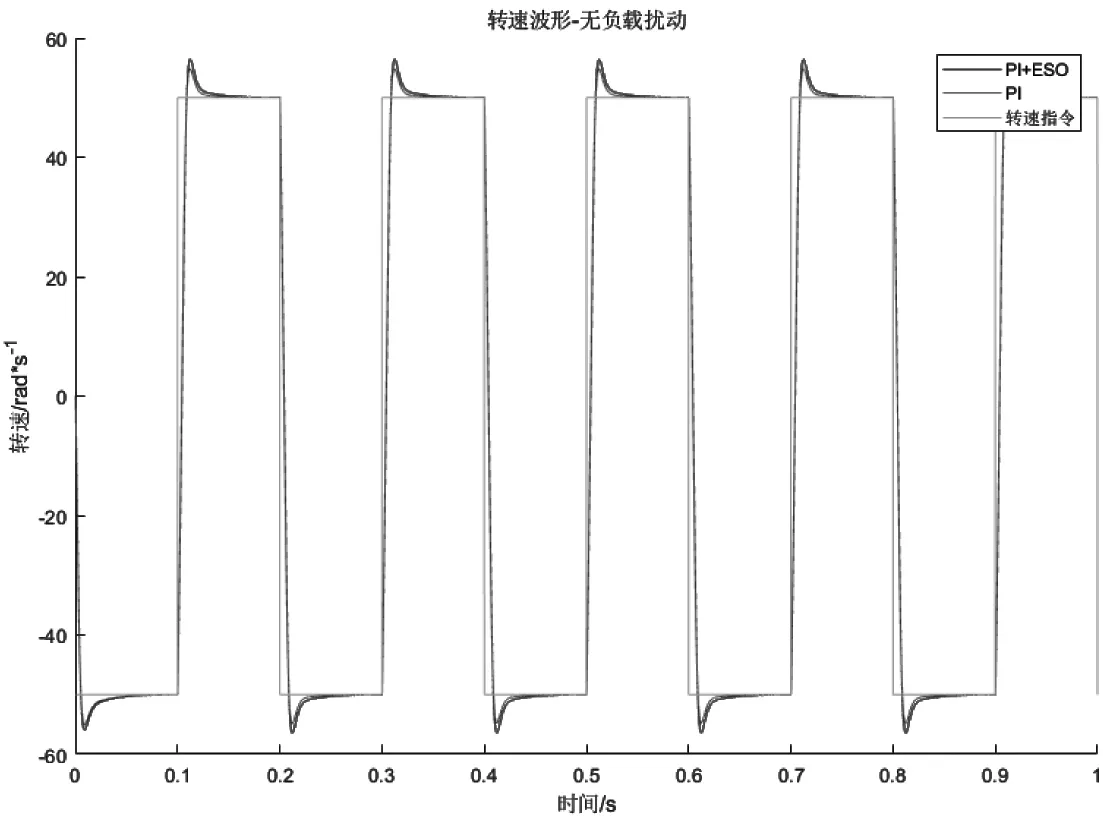
图9 无负载扰动时使用ESO前后性能对比

图10 各频率正弦扰动时不使用ESO时的性能

图11 各频率正弦扰动时使用ESO后的性能

从结果对比中可以看出，使用ESO在不损害系统动态性能的情况下大大提高了系统对于负载力矩扰动的抑制能力，且扰动频率越低，抑制能力越强，和理论分析相吻合。

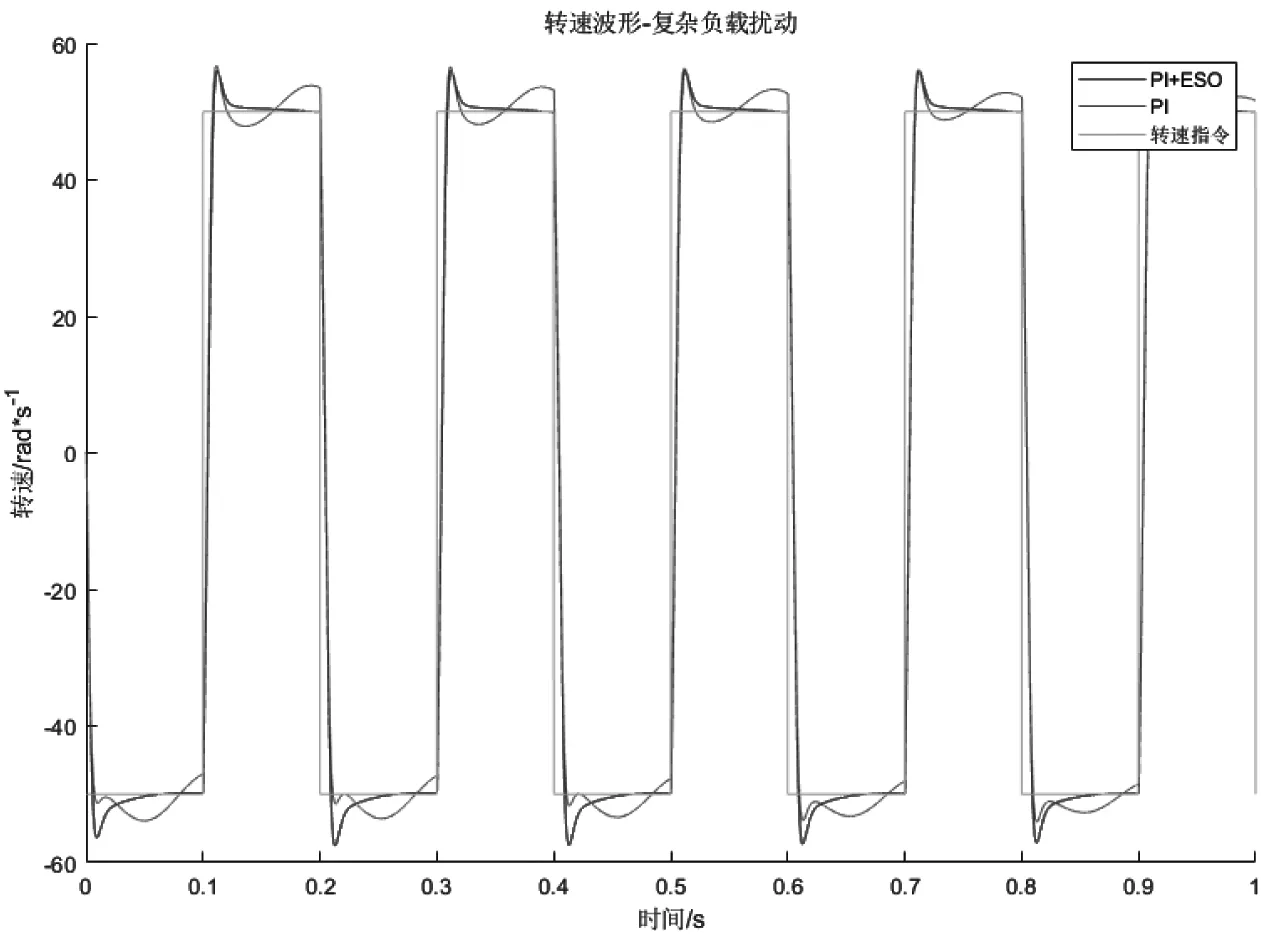
图12 复杂负载扰动时使用ESO前后性能对比

4 结论

本文介绍了基于单框架CMG的两轮自平衡车实现，结合应用特点说明了CMG的电机控制任务。对于用作CMG陀螺的无刷直流电机设计了级联PI控制器并讨论了其参数整定，对于用作CMG框架的永磁交流电机设计了级联PI和扩展状态观测器联合控制器，讨论了ESO的观测性能、参数鲁棒性、稳定性以及测量误差的处理。仿真结果表明两种永磁电机各自取得了较好的控制性能。