融合差分改正的RSSI指纹库室内定位研究
张爱国,邬群勇,孙海信,韩李涛,林聪仁
(1.厦门理工学院 计算机与信息工程学院,福建 厦门 361024; 2.福州大学 数字中国研究院(福建),福建 福州 350003;3.厦门大学 信息科学与技术学院,福建 厦门 361002; 4.山东科技大学 测绘科学与工程学院,山东 青岛 266590)
近年来,室内位置服务需求不断增长,催生了定位技术的不断发展[1-2]。室内复杂的环境给定位带来了困难,使定位精度也远逊于室外的全球卫星导航系统(global navigation satellite system,GNSS)。目前广泛应用的室内定位系统主要有:基站定位、伪卫星定位、指纹定位、UWB(ultra wide band,超宽带)定位、地磁定位、视觉定位、机会信号定位、组合定位、协同定位和导航通讯一体化定位等[3-4],这些定位各具优点,共同为基于位置的服务提供了定位基础。
为消除定位误差,特别是RSSI(received signal strength indicator,接收信号强度指示)指纹库室内定位中的误差,常见的两类消除误差途径为指纹库滤波[5-6]和实时RSSI向量值的差分改正[7]。
为确立RSSI位置指纹定位技术中定位误差与主要影响参数的关系,容晓峰等[8]提出了表示定位平均误差的数学模型,通过计算整个定位区域误差的期望,公式化地表示了接入点个数、接入点摆放位置、采样点间距、最邻近点个数各因素取值不同对定位精度的影响。
为抑制RSSI 误差对无线传感器节点自身定位精度的影响,许多学者以RSSI测距及三边定位算法为基础,提出多种基于RSSI测距误差修正的差分定位算法[9-10]。任维政等[11]在不增加节点硬件设计的情况下,通过RSSI的测量得到节点距离相关信息,以三边测量定位算法为理论基础,提出了基于RSSI的无线传感器网络距离差分修正定位算法。基于RSSI的指纹库定位是目前广为使用的室内定位方法[12],祝正元等[13]为消除指纹库定位中不同终端之间在相同位置接收到相同接入点的RSSI信号值误差,提出采用差分信号强度作为数据库指纹计算定位结果,该方法在差分非采样终端取得了一定的效果,但只是优化和调整了指纹库,并没有校正实时定位过程中的RSSI误差。

图1 融合差分改正的RSSI指纹库定位原理图
室外GNSS定位与室内RSSI定位过程均受到信号传播过程中的环境因素影响。为此,基于RSSI指纹库的室内定位可参考GNSS RTK的差分改正思想[14-15]来消除公共误差,即融合差分改正的RSSI指纹库室内定位。
如图1所示,融合差分改正的RSSI指纹库定位技术是在定位区域选择参考点,根据参考点已知坐标,计算出参考点的坐标改正数或RSSI向量元素改正数,并由参考点实时将这一改正数发送出去。流动站在进行指纹定位的同时,也接收到参考点的改正数,并对其定位结果进行改正,从而提高定位精度。
GNSS定位属于测距后方定位,而RSSI指纹库定位为信号特征定位,这两种方法的定位原理完全不同。在借鉴GNSS RTK差分定位过程中,还需要解决参考点的选择、基于RSSI的差分改正数计算等问题。
1 基于泰森多边形的参考点选择
根据路径因素对误差影响的相关性,距离近则相关性强,所以尽量选择距离待定点较近的参考点参与每次的误差改正数计算。同时,RSSI 越大的参考点,对待定点位置的影响力越大,对待定点位置有更大的决定权。气候学家Thiessen[16]为计算离散分布气象站的平均降雨量所提出的泰森多边形可用于解决最近点、最小封闭圆以及许多空间分析问题。为此,基于泰森多边形能够选择出兼容数量[17-18]且距离合理的参考点。
通过泰森多边形的构建,定位区域被分割成大小不等的多边形,它们之间具有明确的邻接性,便于可达性分析。为此,给定任意一个初始点,首先判断其与泰森多边形之间的所属关系。只要能够确定初始点包含于某个多边形,则利用泰森多边形之间的邻接关系,就能够找到所有的邻接多边形,多边形内的原始三角点即为要选择的定位参考点。
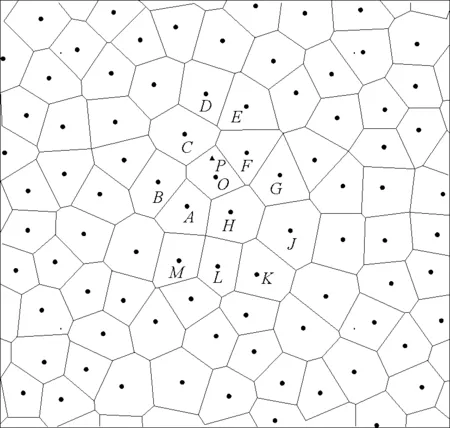
图2 基于泰森多边形的参考点选择
如图2所示的泰森多边形网中有参考点A、B、C、D、E、F、G、H、J、K、L、M、O……,并且P为初始定位点,其所在的泰森多边形的外接圆圆心为O,将其作为本次定位的最近参考点。同时,该多边形有5条边,也即对应有5个外接泰森多边形,它们的外接圆圆心按顺时针方向分别为A、B、C、F、G、H,这些点将作为本次定位的较近参考点。不同的最近参考点对应的泰森多边形可能具有不同数量的外接多边形,比如图2中的参考点H所在的泰森多边形具有6条边,因此有6个较近的周边参考点A、O、G、J、K、L。
通常情况下,初始点包含于泰森多边形之内,但也会出现另外两种特殊情况:一是初始点落在两个相邻泰森多边形的公共边上;二是初始点位于三个及以上的相邻泰森多边形的交点上。在处理这些情况时,须坚持信息不遗漏原则,将尽量多的参考点用于改正数的计算。对第一种情况,选择包含公共边的两个泰森多边形为核心多边形,然后查找与其邻接的所有外接多边形。此时最近参考点有两个,邻近参考点为两个泰森多边形的所有邻接多边形的外接圆圆心。同理,对于第二种情况,此时的核心多边形为包含该点的所有泰森多边形,其外接圆圆心为最近参考点,相应地,这些泰森多边形的所有邻接多边形的外接圆圆心作为邻接参考点。
2 误差改正数计算
在定位过程中,首先进行初始定位,即未经过参考点改正。由该初始定位结果根据包含关系确定其所在的泰森多边形区域,将得到该多边形的中心作为最近的参考点。然后,以此多边形为核心,通过其每条边外接的所有多边形,找到所有外接多边形的中心,这些中心所对应的参考点为距离最近参考点的邻接参考点。
选择参考点的目的是计算误差改正数,在基于RSSI的指纹库定位中,由初始点出发,经实时RSSI向量与指纹库向量的匹配计算等一系列过程,得到待定点的最终坐标。为此,差分改正数可出现在不同的环节,也相应地得到不同的定位结果。本研究分设计坐标改正数与RSSI向量元素改正数两种情况予以叙述。
2.1 坐标改正数
对最后的定位坐标进行改正,此时为坐标改正数计算。坐标改正数将依据初始定位结果所选择到的所有最近参考点和邻接参考点来求取。对于每一个参考点而言,其位置坐标都是已知的,同时,在参考点上的无线设备也可实时采集RSSI信息。为此,参考点位置利用RSSI实时数据的指纹匹配方法同样可得到实时定位坐标结果,只是该结果必定含有路径误差。那么,运用参考点含有误差的实时定位结果减去该点的已知坐标,即可得到参考点对应的误差改正数。坐标改正数的计算过程中,根据每个参考点实时RSSI向量,运用RSSI指纹库定位法,得到其定位结果,并将其已知结果比较,求得误差,然后取误差的平均值作为最后的坐标误差改正数,每个初始定位结果的坐标改正数计算公式如(1)。
(1)
其中,n为参考点的个数,x′i为第i个参考点的RSSI指纹向量定位结果,xi为第i个参考点已知坐标结果,ex、ey为待定点坐标改正数。
2.2 RSSI向量元素改正数计算

图3 差分修正定位算法示意图
除了从整体上改正定位结果的坐标,还可以从底层改正实时RSSI向量元素。每个RSSI向量对应点位置由无线AP数量相等的RSSI值构成。
如图3所示,参考点为N1(RSSI1,RSSI2,…,RSSIm),N2(RSSI1,RSSI2, …,RSSIm),N3(RSSI1,RSSI2, …,RSSIm),Q1(RSSI1,RSSI2, …,RSSIm),Q2(RSSI1,RSSI2, …,RSSIm),…,Q5(RSSI1,RSSI2, …,RSSIm),待定点O。N1、N2、N3是离待定点O最近的参考点,参考点N1到参考点Q1,Q2, …,Q5的距离分别为d11,d12, …,d15;待定点O到参考点Q1,Q2, …,Q5的测量距离分别为d1,d2, …,d5。RSSI向量元素改正数依据外部环境对每个无线AP信号影响大小的不同,从细节层次上采取不同的实时RSSI向量元素值进行改正。
定义1由RSSI向量表示的A、B两点之间距离RD计算公式为:
(2)
其中,RSSIA1为A点RSSI向量的第1个元素,RSSIB1为B点RSSI向量的第1个元素,RSSIA2为A点RSSI向量的第2个元素,RSSIB2为B点RSSI向量的第2个元素,以此类推,m为向量元素个数。
定义2RSSI 向量元素差分修正系数
(3)
其中,RD′ij为第i个最近参考点到第j个邻近参考点的测量距离,RDij为第i个最近参考点到第j个邻近参考点的已知距离,λ为调节系数,n为对应最近参考点的邻近参考点个数,k为最近参考点个数。
定义3待定点的RSSI向量元素差分改正方程为:
RSSIt=RSSI′t-α(RSSI′i-RSSI′it),i=1,2,…,m。
(4)
其中,RSSIi为待定点RSSI向量中的第i个元素的修正值,RSSI′i为待定点RSSI向量中的第i个元素的观测值,RSSI′it为k个最近参考点第t个元素的测量平均值,m为参与定位的参考点个数。
3 融合差分改正的RSSI指纹库定位
在定位区域设置好参考点,并运用第1部分介绍的方法选择参考点之后,配合第2部分的两类误差改正数计算方法,为融合差分改正的RSSI指纹库定位提供了算法基础。依据误差改正数的生成类型,其定位方式也分为基于坐标改正数的定位和基于RSSI向量元素改正数的定位,下面分别予以介绍。
3.1 基于坐标改正数的定位
基于坐标改正数的定位思路简单,易于理解。其核心思想是用初始定位坐标结果减去坐标改正数,同时,该坐标改正数依据初始定位结果所选定的参考点综合确定。基于坐标改正数的定位流程如图4所示。

图4 基于坐标改正数的定位流程
首先获得终端的实时RSSI向量数据,并对该数据运用指纹库进行定位,得到初始定位结果。配合泰森多边形网和地理空间的拓扑分析方法,找到包含该初始定位结果的泰森多边形以及与该多边形相邻的所有邻接泰森多边形。选择这些泰森多边形的外接圆圆心作为参考点计算坐标的差分改正数。由于所有参考点都是固定在定位区域的某个位置,可以随时接收无线定位信息。这些接收到的参考点实时无线RSSI向量数据运用指纹库进行定位,得到参考点含有误差的坐标定位结果。由于参考点的位置固定,即其坐标为已知的值,为此,每个参考点含有误差的定位结果减去其相应的已知值,得到参考点的误差改正数。然后,求取这些选择参考点的误差改正数平均值,作为待定点的坐标误差改正数用于修正初始定位值,即得到待定点剔除误差后的最终结果。
3.2 基于RSSI向量元素改正数的定位
基于RSSI向量元素改正数的定位流程与基于坐标改正数的定位相比,在参考点的选择以前的部分完全相同,只是在参考点之后的改正数计算方法和途径有明显差异,如图5所示。
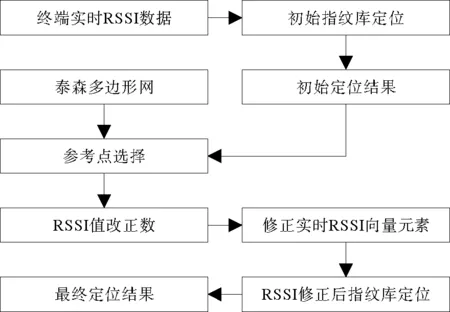
图5 基于RSSI向量元素改正数的定位流程
同样地,从终端实时RSSI数据出发,可以得到包含初始定位结果的一个或多个最近参考点,进而获得所有邻接参考点。由第2部分中的RSSI向量元素改正数计算公式,得出对应初始点的改正系数进而得到每个无线AP对应的RSSI值差分改正数,再分别对RSSI向量元素进行实时修正,得到新的RSSI向量数据。最后,重新运用指纹库定位方法,对终端再次定位,得到最终定位结果。
4 实验及分析
采集某校体育馆数据建立RSSI指纹库,在Eclipse编程环境下,运用Java+PostgreSQL+PostGIS+Mybatis开发工具制作算法程序,实验验证了提出的融合差分改正的RSSI指纹库定位算法的可行性和准确率。
4.1 实验场景及数据准备
实验场景设置了如图6所示的36个参考点,其坐标如表1所示,然后,采用QGIS软件的QGIS geo-algorithms-Vector geometry tools-Voronoi polygons功能构建的泰森多边形如图6所示。

表1 参考点坐标表

图6 参考点的泰森多边形
为了能够快速有效地对这些泰森多边形进行空间关系计算,将图6中的参考点和多边形均作为空间对象存储于PostgreSQL/PostGIS中,其存储效果如图7所示,st、astext字段为泰森多边形几何对象。
4.2 实验过程
给定实时RSSI向量数据(-54,-54,-77,-53,-59,-61,-65,-65,-65,-66,-66,-63,-76,-76,-51,-54,-72,-62,-54),运用张爱国等[19]提出的方法得到其初始定位结果为(5, 6)。从空间数据关系操作到差分改正数计算的整个实验过程为:
1) 根据PostGIS的空间拓扑包含关系函数st.contains(Geometry,point),给定初始定位结果(5,6),得到包含该点的泰森多边形对应的id为12。

图7 泰森多边形在PostGIS中的几何对象存储
2) 运用PostGIS的空间拓扑邻接关系函数st-intersects(Geometry,Geometry),确定与id为12的泰森多边形相邻接的多边形id集合{11,12,14,16,21,24,26,32,36}。
3) 运用PostGIS的空间拓扑所属关系函数st-within(Geometry,Geometry),获得2)中相邻接多边形对应的参考点id集合{24,12,11,4,1,19,14,20,7}。
4) 坐标改正数计算
在Eclipse编程环境下,开发Java功能类,实现坐标改正数的计算。
空间数据表设计:数据表的字段结构如表2。

表2 空间数据表结构设计
在QGIS软件中,用labels功能找到参考点与对应id的多边形,然后,把各自的参考点与多边形原始数据合成一个包含参考点和多边形的空间数据文件。最后,采用插入方式得到该数据表数据。
5) RSSI向量元素改正数计算
在坐标改正数的基础上,添加了RSSI向量元素改正系数的计算,通过逐次定位改正每个元素的值。
4.3 实验效果及分析
为了体现本算法的定位效果,运用如下方法,在已有实测420条指纹数据基础上,构建了21 000条实时指纹数据。
根据实时指纹数据主要受距离远近和其他综合因素的影响,即距离影响误差的大小,距离越远RSSI值越不稳定。为此,实时RSSI数据由指纹库中RSSI数据+距离d+正态分布随机数δ,该实时RSSI数据
RSSIrealtime=RSSIfingerprint+λD+δ,
(5)
其中,距离D=10|RSSI-RSSI0|/(10×n)。
RSSI0为1 m处的信号强度,取值为-37 db,n为路径损耗指数,取值3。
正态分布随机数δ表示综合因素的影响,δ服从正态分布N(μ,σ2),本实验取值μ=0、σ=1.0。将实时数据代入系统运算,运行硬件为DELL Inspiron137000 Series笔记本电脑,软件环境为Linux+Eclipse+PostgreSQL/PostGIS+Mybatis。在选定5个参考点的情况下,坐标改正数计算耗时0.282 s,RSSI向量元素改正数计算耗时0.083 s。同时,本算法与WKNN算法的运行结果对比如表3所示。
基于Wi-Fi RSSI指纹库的室内定位算法时间复杂度为O(6mn+6n2),WKNN的时间复杂度为O(6mn+6n2+3k+1)[20],其中m表示RSSI元素个数,n表示区域网格个数,k表示WKNN中取的k个最小样值。本定位算法相对于初始的指纹库而言,坐标差分方法增加了参考点的定位,向量元素差分方法在坐标差分的基础上增加了每个元素的计算,为此,坐标差分方法的时间复杂度为O((6mn+6n2)×r),向量元素差分方法的时间复杂度为O((6mn+6n2)×r+m),其中r表示每次定位泰森多边形确定的参考点个数。本实验各参数取值情况为m=20、n=420、k=4、r≈6。从表3可以看出,本算法在耗时方面,向量元素差分>坐标差分>WKNN,这是由于差分改正需要泰森多边形的判定操作所致。另外,基于向量元素的改正计算公式相比坐标改正复杂,所以耗时也有少量增加。在算法的定位准确率上,基于坐标或向量元素的改正WKNN算法均有一定的提高。

表3 定位实验效果表
5 结论
在基于RSSI的指纹库室内定位中,由于信号传播等环境因素的影响,造成实时RSSI向量数据的不稳定,从而降低了指纹库的定位精度。依据在定位区域中实时RSSI传播的地理相关性,提出融合差分定位的RSSI指纹库定位方法。设计了基于邻接泰森多边形用于计算差分数据的参考点选择;然后,分别叙述两种情况下的差分改正数的求解,即差分坐标改正数和RSSI向量元素改正数;接着,给出了融合差分改正的RSSI指纹库定位流程;最后,用Java+PostgreSQL+PostGIS+Mybatis设计了算法程序,并使用实时数据进行了测试。从实验效果看出,提出的算法具有可行性,在定位准确性上相较于WKNN算法有一定的提高。

